空间点线面的位置关系及公理

空间点线面之间的位置关系一．平面的基本性质：公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. 公理2：如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.公理3：经过不在同一条直线上的三点，有且只有一个平面.推论1:经过一条直线和直线外的一点有且只有一个平面.推论2:经过两条相交直线有且只有一个平面.推论3:经过两条平行直线有且只有一个平面.二．空间直线与平面之间的位置关系：1.直线与平面的位置关系可分为：直线在平面内；直线与平面平行；直线成平面相交；2.平面与平面之间位置关系分为：面面平行；面面相交；面面重合；3.空间直线之间的位置关系：相交，平行，异面；三．等角定理、平行公理：定理：如果一个角的两边和另一个角的两边分别平行，那么这两个角相等或互补；推论：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等；平行公理：平行与同一条直线的两条直线平行；空间平行具有传递性，空间平行平面也具有传递性；四．证明方法：1.证明三点共线的常用方法：（1）首先找出两个平面，然后证明这三点都是这两个平面的公共点。

由公理三得证；（2）选择其中两点确定一条直线，然后证明另一点也在其上；2.证明直线共面通常的方法：()1先由其中两条直线确定一个平面，再证明其余的直线都在此平面内（纳入法）；()2分别过某些点作多个平面，然后证明这些平面重合（重合法）；()3也可利用共面向量定理来证明.3.证明三线共点的方法：先证两条直线交于一点，再证明第三条直线经过这点，转化为证明点在线上的问题；()1如果A、B是交点，那么AB是交线；()2如果两个不同平面有三个或者更多的交点，那么它们共面；()3如果lαβ=∈，点P是α、β的一个公共点，那么P l4.证明几点共面的问题可以先取三点（不共线的三点）确定一个平面，再证其余各点都在这个平面内；1.分别和两条异面直线平行的两条直线的位置关系是： A ．一定平行 B.一定相交 C.一定异面 D.相交或异面2.如果在两个平面内分别各有一条直线，这两条直线互相平行，那么这两个平面的位置关系为： A ．平行 B.相交 C.平行或相交 D.垂直或相交3.已知下列命题：其中真命题的个数为： ； （1）若直线l 平行于α内无数条直线，则 l α；（2）若直线l 在平面α外，则 l α； （3）若直线 a b ，直线⊂b α，则 a α； （4）若直线 a b ，⊂b α，那么直线a 平行于平面α内的无数条直线；4.空间三条直线互相平行，由每两条平行直线确定一个平面，则可确定平面的个数为：5.若三个平面两两相交，且三条交线互相平行，则这三个平面将空间分成 部分；6.如果两条异面直线称为一对，那么在正方体的十二条棱中，共有异面直线 对；7.空间中有四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的； .A 充分非必要条件；.B 必要非充分条件；.C 充要条件；.D 非充分非必要条件．8.不共面的四个定点到平面α的距离都相等，这样的平面α共有.A 3个 .B 4个 .C 6个 .D 7个9.已知两个不同的平面α、β和两条不重合的直线，m 、n ，有下列四个命题 ①若α⊥m n m ,//，则α⊥n ②若βαβα//,,则⊥⊥m m③若βαβα⊥⊂⊥则,,//,n n m m ④若n m n m //,,,//则=βαα其中正确命题的个数是 A ．0个 B ．1个 C ．2个 D ．3个 10.设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题： ①若m ⊥α，n ∥α，则m ⊥n ；②若α∥β，β∥γ，m ⊥α，则m ⊥γ； ③若m ∥α，n ∥α，则m ∥n ；④若α⊥γ，β⊥γ，则α∥β．其中正确命题的序号是 A ．①和② B ．②和③ C ．③和④ D ．①和④ 11.已知直线a 、b 、c 和平面M ，则可以得到a//b 的是 ： ；A.a//M ，b//MB.a ⊥c ，b ⊥cC.a 、b 与平面M 成等角D.a ⊥M ，b ⊥M ． 12.已知直线m 、n 平面βα,，下列命题中正确的是A.若直线m 、n 与平面α所成的角相等，则m//nB.若m ⊥α，n ⊥β，α⊥β，则m ⊥nC.若m ⊂α，β⊂n ，m//n ，则α//βD.若m//α,,//,//βαβn 则m//n13.已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（ ）A ．,,m n m n αα若则‖‖‖B ．,,αγβγαβ⊥⊥若则‖C ．,,m m αβαβ若则‖‖‖D ．,,m n m n αα⊥⊥若则‖14.已知βα,是相异两平面，n m ,是相异两直线，则下列命题中不正确．．．的是 （ ） A.若m ∥α⊥m n ,，则α⊥n B.若⊥m βα⊥m ,，则α∥β C.若⊥m βα⊂m ,，则⊥αβ D.若m ∥n =⋂βαα,，则m ∥n 15.设有直线m 、n 和平面α、β.下列四个命题中，正确的是( )A.若m ∥α,n ∥α,则m ∥n ；B.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β，m ⊂α,则m ⊥β；D.若α⊥β，m ⊥β，m ⊄α,则m ∥α 16.已知n m ,是两条不同的直线，βα,为两个不同的平面，有下列四个命题： ①若βα⊥⊥n m ,，m ⊥n ，则βα⊥；②若n m n m ⊥,//,//βα，则βα//； ③若n m n m ⊥⊥,//,βα，则βα//；④若βαβα//,//,n m ⊥，则n m ⊥． 其中正确的命题是（填上所有正确命题的序号）_______________．17.正方体1111ABCD A B C D -中，P 、Q 、R 分别是AB 、AD 、11B C 的中点． 那么，正方体的过P 、Q 、R 的截面图形是.A 三角形.B 四边形.C 五边形.D 六边形18.如图，l αβ= ，A 、B α∈，C β∈，且C l ∉，直线AB l M = ，过A 、B 、C 三点 的平面记作γ，则γ与β的交线必通过.A 点A ； .B 点B ； .C 点C 但不通过点M ； .D 点C 和点MAB CD 1A 1B 1C 1D PD RαβlM A B C题型二：证明点共线，线共点，点共面，线共面问题 例1.点共面：1.（07江苏）如图，已知1111ABCD A B C D -是棱长为3的正方体，点E 在1AA 上，点F 在1CC 上，且11AE FC ==.求证：1,,,E B F D 四点共面；2.（08四川）如图，平面ABEF ⊥平面ABCD ，四边形ABEF 与ABCD 都是直角梯形，90BAD FAB ∠=∠=︒，BC ∥12AD ，BE ∥12AF ．证明：C 、D 、F 、E 四点共面；例3.线共面：1.已知：a ，b ，c ，d 是不共点且两两相交的四条直线，求证：a ，b ，c ，d 共面。

高中空间点线面之间位置关系知识点总结第二章直线与平面的位置关系空间点、直线、平面之间的位置关系D C1平面含义：平面是无限延展的α2平面的画法及表示A B 〔1〕平面的画法：水平放置的平面通常画成一个平行四边形，锐角画成450，且横边画成邻边的倍长〔如图〕〔2〕平面通常用希腊字母α、β、γ等表示，如平面α、平面β等，也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示，如平面AC、平面ABCD等。

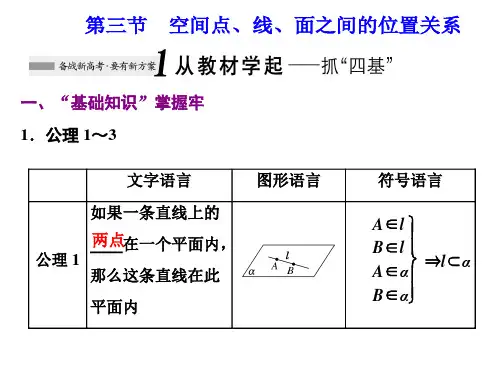
三个公理：1〕公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内符号表示为A∈LB∈L=>LαA α·A∈αLB∈α公理1作用：判断直线是否在平面内〔2〕公理2：过不在一条直线上的三点，有且只有一个平面。

A B符号表示为：A、B、C三点不共线=>有且只有一个平面α，α·C·使A∈α、B∈α、C∈α。

·公理2作用：确定一个平面的依据。

〔3〕公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

β符号表示为：P∈α∩β=>α∩β=L，且P∈L公理3作用：判定两个平面是否相交的依据αPL空间中直线与直线之间的位置关系·空间的两条直线有如下三种关系：相交直线：同一平面内，有且只有一个公共点；共面直线平行直线：同一平面内，没有公共点；异面直线：不同在任何一个平面内，没有公共点。

2公理4：平行于同一条直线的两条直线互相平行。

符号表示为：设a、b、c是三条直线a∥b=>a∥c3c∥b强调：公理4实质上是说平行具有传递性，在平面、空间这个性质都适用。

公理4作用：判断空间两条直线平行的依据。

等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补注意点：①a'与b'所成的角的大小只由a、b的相互位置来确定，与O的选择无关，为简便，点O一般取在两直线中的一条上；②两条异面直线所成的角θ∈(0，)；③当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a⊥b；2④两条直线互相垂直，有共面垂直与异面垂直两种情形；⑤计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。

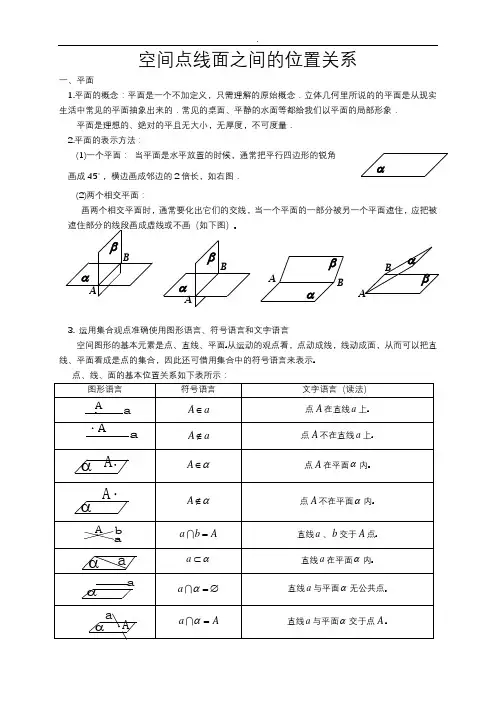
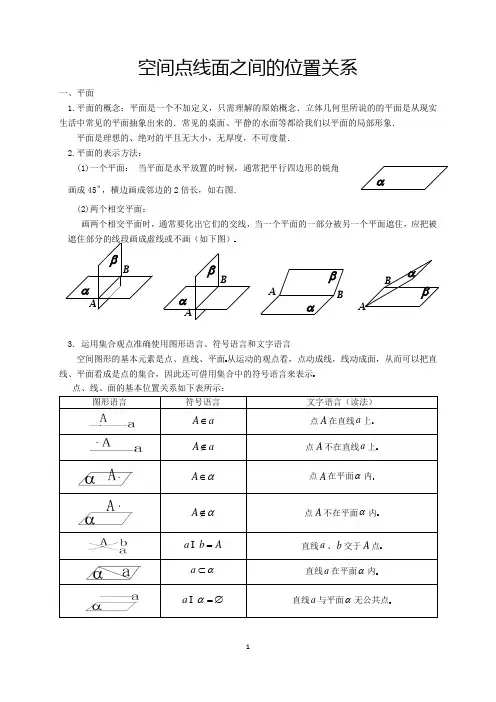
空间点线面之间的位置关系一、平面1.平面的概念：平面是一个不加定义，只需理解的原始概念．立体几何里所说的的平面是从现实生活中常见的平面抽象出来的．常见的桌面、平静的水面等都给我们以平面的局部形象．平面是理想的、绝对的平且无大小，无厚度，不可度量． 2.平面的表示方法：(1)一个平面： 当平面是水平放置的时候，通常把平行四边形的锐角 画成45，横边画成邻边的2倍长，如右图． (2)两个相交平面：画两个相交平面时，通常要化出它们的交线，当一个平面的一部分被另一个平面遮住，应把被遮住部分的线段画成虚线或不画（如下图）3. 运用集合观点准确使用图形语言、符号语言和文字语言空间图形的基本元素是点、直线、平面从运动的观点看，点动成线，线动成面，从而可以把直线、平面看成是点的集合，因此还可借用集合中的符号语言来表示点、线、面的基本位置关系如下表所示：b A =a α⊂α=∅ αBAβαABαβαβBAAβαBAα=l β= 二、平面的基本性质1. 公理1 如果一条直线的两点在一个平面内，那么这条直线在这个平面内推理模式：A AB B ααα∈⎫⇒⊂⎬∈⎭． 如图示： 或者：∵,A B αα∈∈，∴AB α⊂ 公理1的作用：①判定直线是否在平面内；②判定点是否在平面内； ③检验面是否是平面．2. 公理2 经过不在同一条直线上的三点，有且只有一个平面推理模式：,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者：∵,,A B C 不共线，∴存在唯一的平面α，使得,,A B C α∈. 推论1：经过一条直线和这条直线外的一点，有且只有一个平面； 推论2：经过两条相交直线，有且只有一个平面； 推论3：经过两条平行直线，有且只有一个平面．(1)以上是确定平面的四个不同的条件，是判断两个平面重合的依据，是证明点线共面的依据，也是作截面、辅助面的依据．(2)“有且只有一个”的含义要准确理解．这里的“有”是说图形的存在，“只有一个”是说图形唯一．因此，在证明有关这类语句的命题时，要从“存在性”和“唯一性”两方面来论证． 2. 公理3 如果两个不重合的平面有一个公共点,有且只有一条过该点的公共直线推理模式：A A l A ααββ∈⎫⇒∈=⎬∈⎭如图示：或者：∵,A A αβ∈∈，∴,l A l αβ=∈公理3的作用：(1)判断两个平面是否相交及交线位置； (2)判断点是否在线上 1、证明空间三点共线问题通常证明这些点都在两个平面的交线上，即先确定出某两点在两个平面的交线上，再证明第三点既在第一个平面内，又在第二个平面内。

公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内(即直线在平面内)．公理2：经过不在同一条直线上的三点，有且只有一个平面(即可以确定一个平面)．公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条通过这个点的公共直线．公理4：平行于同一条直线的两条直线平行．2．直线与直线的位置关系(1)位置关系的分类(2)异面直线所成的角①定义：过空间任意一点P 分别引两条异面直线a ，b 的平行线l 1，l 2(a ∥l 1，b ∥l 2)，这两条相交直线所成的锐角(或直角)叫作异面直线a ，b 所成的角(或夹角)．②范围：(]0，π2. 3．直线与平面的位置关系有直线在平面内、直线与平面相交、直线与平面平行三种情况．4．平面与平面的位置关系有平行、相交两种情况．5．等角定理 空间中，如果两个角的两边分别对应平行，那么这两个角相等或互补．【知识拓展】1．唯一性定理(1)过直线外一点有且只有一条直线与已知直线平行．(2)过直线外一点有且只有一个平面与已知直线垂直．(3)过平面外一点有且只有一个平面与已知平面平行．(4)过平面外一点有且只有一条直线与已知平面垂直．2．异面直线的判定定理经过平面内一点的直线与平面内不经过该点的直线互为异面直线．判断下列结论是否正确(请在括号中打“√”或“×”)(1)如果两个不重合的平面α，β有一条公共直线a，就说平面α，β相交，并记作α∩β＝a.()(2)两个平面α，β有一个公共点A，就说α，β相交于过A点的任意一条直线．()(3)两个平面ABC与DBC相交于线段BC.()(4)经过两条相交直线，有且只有一个平面．()(5)没有公共点的两条直线是异面直线．()1．下列命题正确的个数为()①梯形可以确定一个平面；②若两条直线和第三条直线所成的角相等，则这两条直线平行；③两两相交的三条直线最多可以确定三个平面；④如果两个平面有三个公共点，则这两个平面重合．A．0 B．1 C．2 D．32．(2016·浙江)已知互相垂直的平面α，β交于直线l.若直线m，n满足m∥α，n⊥β，则()A．m∥l B．m∥n C．n⊥l D．m⊥n3．(2016·合肥质检)已知l，m，n为不同的直线，α，β，γ为不同的平面，则下列判断正确的是()A．若m∥α，n∥α，则m∥nB．若m⊥α，n∥β，α⊥β，则m⊥nC．若α∩β＝l，m∥α，m∥β，则m∥lD．若α∩β＝m，α∩γ＝n，l⊥m，l⊥n，则l⊥α4.(教材改编)如图所示，已知在长方体ABCD－EFGH中，AB＝23，AD＝23，AE＝2，则BC和EG所成角的大小是______，AE 和BG所成角的大小是________．5．如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，则直线EF与正方体的六个面所在的平面相交的平面个数题型一 平面基本性质的应用例1 (1)(2016·山东)已知直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件(2)已知空间四边形ABCD (如图所示)，E 、F 分别是AB 、AD 的中点，G 、H 分别是BC 、CD 上的点，且CG ＝13BC ，CH ＝13DC .求证：①E 、F 、G 、H 四点共面；②三直线FH 、EG 、AC 共点．如图，平面ABEF ⊥平面ABCD ，四边形ABEF 与四边形ABCD 都是直角梯形，∠BAD ＝∠F AB ＝90°，BC ∥AD 且BC ＝12AD ，BE ∥AF 且BE ＝12AF ，G 、H 分别为F A 、FD 的中点． (1)证明：四边形BCHG 是平行四边形；(2)C 、D 、F 、E 四点是否共面？为什么？题型二 判断空间两直线的位置关系例2 (1)(2015·广东)若直线l 1和l 2是异面直线，l 1在平面α内，l 2在平面β内，l 是平面α与平面β的交线，则下列命题正确的是( )A ．l 与l 1，l 2都不相交B ．l 与l 1，l 2都相交C ．l 至多与l 1，l 2中的一条相交D ．l 至少与l 1，l 2中的一条相交(2)如图，在正方体ABCD －A 1B 1C 1D 1中，M ，N 分别是BC 1，CD 1的中点，则下列判断错误的是( )A ．MN 与CC 1垂直B ．MN 与AC 垂直C ．MN 与BD 平行 D ．MN 与A 1B 1平行(3)在图中，G 、N 、M 、H 分别是正三棱柱(两底面为正三角形的直棱柱)的顶点或所在棱的中点，则表示直线GH 、MN 是异面直线的图形有________．(填上所有正确答案的序号)(1)已知a，b，c为三条不重合的直线，有下列结论：①若a⊥b，a⊥c，则b∥c；②若a⊥b，a⊥c，则b⊥c；③若a∥b，b⊥c，则a⊥c.其中正确的个数为()A．0 B．1 C．2 D．3(2)(2016·南昌一模)已知a、b、c是相异直线，α、β、γ是相异平面，则下列命题中正确的是()A．a与b异面，b与c异面⇒a与c异面B．a与b相交，b与c相交⇒a与c相交C．α∥β，β∥γ⇒α∥γD．a∥α，b∥β，α与β相交⇒a与b相交题型三求两条异面直线所成的角例3(2016·重庆模拟)如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，则异面直线AP与BD所成的角为________．已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为()A.16 B.36 C.13 D.3316．构造模型判断空间线面位置关系典例已知m，n是两条不同的直线，α，β为两个不同的平面，有下列四个命题：①若m⊥α，n⊥β，m⊥n，则α⊥β；②若m∥α，n∥β，m⊥n，则α∥β；③若m⊥α，n∥β，m⊥n，则α∥β；④若m⊥α，n∥β，α∥β，则m⊥n.其中所有正确的命题是________．1．设a，b是两条不同的直线，α，β是两个不同的平面，aα，b⊥β，则“α∥β”是“a⊥b”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件2．(2016·福州质检)在三棱柱ABC－A1B1C1中，E、F分别为棱AA1、CC1的中点，则在空间中与直线A1B1、EF、BC都相交的直线() A．不存在B．有且只有两条C．有且只有三条D．有无数条3．对于任意的直线l与平面α，在平面α内必有直线m，使m与l()A．平行B．相交C．垂直D．互为异面直线4．在四面体ABCD的棱AB，BC，CD，DA上分别取E，F，G，H四点，如果EF与HG交于点M，则() A．M一定在直线AC上B．M一定在直线BD上C．M可能在AC上，也可能在BD上D．M既不在AC上，也不在BD上5．四棱锥P－ABCD的所有侧棱长都为5，底面ABCD是边长为2的正方形，则CD与P A所成角的余弦值为()A.255 B.55 C.45 D.356．下列命题中，正确的是()A．若a，b是两条直线，α，β是两个平面，且aα，bβ，则a，b是异面直线B．若a，b是两条直线，且a∥b，则直线a平行于经过直线b的所有平面C．若直线a与平面α不平行，则此直线与平面内的所有直线都不平行D．若直线a∥平面α，点P∈α，则平面α内经过点P且与直线a平行的直线有且只有一条7．(2016·南昌高三期末)如图，在直三棱柱ABC－A1B1C1中，底面为直角三角形．∠ACB＝90°，AC＝6，BC＝CC1＝2，P是BC1上一动点，则CP＋P A1的最小值为________．8.如图是正四面体(各面均为正三角形)的平面展开图，G、H、M、N分别为DE、BE、EF、EC的中点，在这个正四面体中，①GH与EF平行；②BD与MN为异面直线；③GH与MN成60°角；④DE与MN垂直．以上四个命题中，正确命题的序号是________．9．(2015·浙江)如图，三棱锥ABCD中，AB＝AC＝BD＝CD＝3，AD＝BC＝2，点M，N分别是AD，BC的中点，则异面直线AN，CM所成的角的余弦值是________．10.(2016·郑州质检)如图，矩形ABCD中，AB＝2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点，则在△ADE翻折过程中，下面四个命题中不正确的是________．①BM是定值；②点M在某个球面上运动；③存在某个位置，使DE⊥A1C；④存在某个位置，使MB∥平面A1DE.12.如图所示，等腰直角三角形ABC中，∠A＝90°，BC＝2，DA⊥AC，DA⊥AB，若DA＝1，且E为DA的中点．求异面直线BE 与CD所成角的余弦值．13.已知正方体ABCD－A1B1C1D1中，E，F分别为D1C1，C1B1的中点，AC∩BD＝P，A1C1∩EF＝Q.求证：(1)D、B、F、E四点共面；(2)若A1C交平面DBFE于R点，则P，Q，R三点共线．。