必修二空间几何证明经典题型

高中必修二空间几何练习题及讲解### 高中必修二空间几何练习题及讲解#### 练习题一：点、线、面的位置关系题目：在空间直角坐标系中，设点A(2, 3, 4)，点B(-1, -2, 1)，求证线段AB与平面x+y+z=6垂直。

解答：首先，我们需要找到线段AB的方向向量。

设向量\(\vec{AB} =\vec{b} - \vec{a}\)，其中\(\vec{a} = (2, 3, 4)\)，\(\vec{b} = (-1, -2, 1)\)。

计算得到\(\vec{AB} = (-3, -5, -3)\)。

接下来，我们观察平面x+y+z=6的法向量。

由平面方程可知，其法向量为\(\vec{n} = (1, 1, 1)\)。

要证明线段AB与平面垂直，需要证明\(\vec{AB} \cdot \vec{n} =0\)。

计算点积：\((-3) \times 1 + (-5) \times 1 + (-3) \times 1 = -3 - 5 - 3 = -11\)。

由于点积不为零，线段AB与平面x+y+z=6不垂直。

题目中的结论是错误的。

#### 练习题二：空间几何体的体积计算题目：已知一个正四面体的高为h，求其体积。

解答：正四面体的体积公式为\(V = \frac{1}{3}Bh\)，其中B是底面积。

正四面体的底面是一个正三角形，设正四面体的边长为a，则底面积B 可以通过公式\(B = \frac{\sqrt{3}}{4}a^2\)计算。

由于正四面体的高h与边长a有如下关系：\(h =\frac{\sqrt{2}}{2}a\)。

将h代入体积公式，得到\(V = \frac{1}{3} \times\frac{\sqrt{3}}{4}a^2 \times \frac{\sqrt{2}}{2}a =\frac{\sqrt{2}}{12}a^3\)。

#### 练习题三：空间直线与平面的交点题目：已知直线l: \(x = 2t + 1\), \(y = 1 - t\), \(z = 3 - 4t\)，平面π: \(2x - y + z - 5 = 0\)，求直线l与平面π的交点。

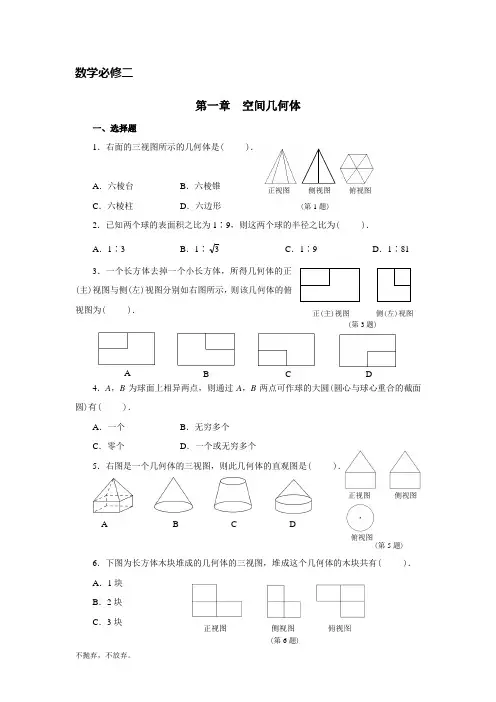
数学必修二第一章 空间几何体一、选择题1．右面的三视图所示的几何体是( )．A ．六棱台B ．六棱锥C ．六棱柱D ．六边形 (第1题)2．已知两个球的表面积之比为1∶9，则这两个球的半径之比为( )． A ．1∶3B ．1∶3C ．1∶9D ．1∶813．一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如右图所示，则该几何体的俯视图为( )．4．A ，B 为球面上相异两点，则通过A ，B 两点可作球的大圆(圆心与球心重合的截面圆)有( )．A ．一个B ．无穷多个C ．零个D ．一个或无穷多个5．右图是一个几何体的三视图，则此几何体的直观图是( )． )．A B C D6．下图为长方体木块堆成的几何体的三视图，堆成这个几何体的木块共有( )． A ．1块 B ．2块 C ．3块正(主)视图侧(左)视图ABCD(第3题)正视图侧视图俯视图(第5题)正视图俯视图侧视图(第6题)D．4块7．关于斜二测画法画直观图说法不正确的是()．A．在实物图中取坐标系不同，所得的直观图有可能不同B．平行于坐标轴的线段在直观图中仍然平行于坐标轴C．平行于坐标轴的线段长度在直观图中仍然保持不变D．斜二测坐标系取的角可能是135°8．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是()．①正方体②圆锥③三棱台④正四棱锥(第8题)A．①②B．①③C．①④D．②④9．一正方体的各顶点都在同一球面上，用过球心的平面去截这个组合体，截面图不能是()．A B C D10．如果一个三角形的平行投影仍然是一个三角形，则下列结论正确的是()．A．原三角形的内心的平行投影还是投影三角形的内心B．原三角形的重心的平行投影还是投影三角形的重心C．原三角形的垂心的平行投影还是投影三角形的垂心D．原三角形的外心的平行投影还是投影三角形的外心二、填空题11．一圆球形气球，体积是8 cm3，再打入一些空气后，气球仍然保持为球形，体积是27 cm3．则气球半径增加的百分率为．12．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的体对角线的长分别是9和15，则这个棱柱的侧面积是．13．右图是一多面体的展开图，每个面内都给了字母，请根据要求回答问题：①如果A 是多面体的下底面，那么上面的面是 ； ②如果面F 在前面，从左边看是面B ，那么上面的面是 ．14．一个几何体的三视图如下图所示，则此几何体的体积是 ．三、解答题15．圆柱内有一个四棱柱，四棱柱的底面是圆柱底面的内接正方形．已知圆柱表面积为6 ，且底面圆直径与母线长相等，求四棱柱的体积．16．下图是一个几何体的三视图(单位：cm ) (1)画出这个几何体的直观图(不要求写画法)； (2)求这个几何体的表面积及体积.(第14题)4俯视图正视图侧视图4 43俯视图A BC B ＇A ＇ C ＇1 1 正视图B ＇B A ＇A 3 侧视图ABC1 (第16题)(第13题)17．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕直线AD 旋转一周所成几何体的表面积及体积．18．已知正方体、球、底面直径与母线相等的圆柱，它们的表面积相等，试比较它们的体积V 正方体，V 球，V 圆柱的大小．19．如图，一个圆锥形容器的高为a ，内装有一定量的水．如果将容器倒置，这时水所形成的圆锥的高恰为2a，求原来水面的高度．20．如图，四棱柱的底面是菱形，各侧面都是长方形．两个对角面也是长方形，面积分别为Q 1，Q 2．求四棱柱的侧面积．第二章 点、直线、平面之间的位置关系一、选择题1．垂直于同一条直线的两条直线一定( )． A ．平行B ．相交C ．异面D ．以上都有可能2．正四棱柱1111D C B A ABCD 中，AB AA 2＝1，则异面直线11AD B A 与所成角的余弦值为( )．(第20题)(第19题)(第17题)A ．51 B ．52 C ．53 D ．54 3．经过平面外两点与这个平面平行的平面( )． A ．可能没有B ．至少有一个C ．只有一个D ．有无数个4．点E ，F ，G ，H 分别为空间四边形ABCD 中AB ，BC ，CD ，AD 的中点，若AC ＝BD ，且AC 与BD 所成角的大小为90°，则四边形EFGH 是（ ）．A ．菱形B ．梯形C ．正方形D ．空间四边形5．已知 m ，n 为异面直线，m ⊂平面 ，n ⊂平面 β，∩ ＝l ，则( )． A ．l 与m ，n 都相交 B ．l 与m ，n 中至少一条相交C ．l 与m ，n 都不相交D ．l 只与m ，n 中一条相交6．在长方体ABCD -A 1B 1C 1D 1中，AB ＝AD ＝23，CC 1＝2，则二面角C 1-BD -C 的大小为( )．A ．30°B ．45°C ．60°D ．90°7．如果平面外有两点A ，B ，它们到平面 的距离都是a ，则直线AB 和平面的位置关系一定是( )．A ．平行B ．相交C ．平行或相交D ．AB ⊂8．设m ，n 是两条不同的直线，，是两个不同的平面．下列命题中正确的是( )．A ．⊥，m ⊥，n ∥⇒m ⊥nB ．∥，m ⊥，n ∥⇒m ⊥nC ．m ⊥，n ⊂，m ⊥n ⇒⊥D ．⊥，∩＝m ，n ⊥m ⇒n⊥9．平面∥平面，AB ，CD 是夹在 和 之间的两条线段，E ，F 分别为AB ，CD 的中点，则EF 与 的关系是( )．A ．平行B ．相交C ．垂直D ．不能确定10．平面 ⊥平面 ，A ∈α，B ∈β，AB 与两平面 ，β所成的角分别为4π和6π，过A ，B 分别作两平面交线的垂线，垂足为A ′，B′，则AB ∶A ′B ′ 等于( )．A ．2∶1B ．3∶1C ．3∶2D ．4∶3二、填空题11．下图是无盖正方体纸盒的展开图，在原正方体中直线AB ，CD 所成角的大小为 ．12．正三棱柱ABC -A 1B 1C 1的各棱长均为2，E ，F 分别是AB ，A 1C 1的中点，则EF 的长是 ．13．如图，AC 是平面 的斜线，且AO ＝a ，AO 与 成60º角，OC ，AA ′⊥于A ′，∠A ′OC ＝45º，则点A 到直线OC 的距离是 ．(第13题)14．已知正四棱锥的底面边长为2，侧棱长为5，则侧面与底面所成二面角的大小为 ．15．已知a ，b 为直线，为平面，a ∥，b ∥，对于a ，b 的位置关系有下面五个(第12题)AB CA 1B 1C 1EFDCAB(第11题)结论：①平行；②垂直不相交；③垂直相交；④相交；⑤不垂直且不相交． 其中可能成立的有 个．三、解答题16．正方体AC 1的棱长为a ． (1)求证：BD ⊥平面ACC 1A 1；(2)设P 为D 1D 中点，求点P 到平面ACC 1A 1的距离．17．如图，ABCD 是正方形，O 是该正方形的中心，P 是平面ABCD 外一点，PO 底面ABCD ，E 是PC 的中点．求证：(1)P A ∥平面BDE ； (2)BD ⊥平面P AC ．18．如图，在四棱锥P -ABCD 中，PD ⊥平面ABCD ，PD ＝DC ＝BC ＝1，AB ＝2，AB ∥DC ，∠BCD ＝90°．(1)求证：PC ⊥BC ；(2)求点A 到平面PBC 的距离．19．如图，棱长为1的正方体ABCD -A 1B 1C 1D 1中， (1)求证：AC ⊥平面B 1D 1DB ； (2)求证：BD 1⊥平面ACB 1； (3)求三棱锥B -ACB 1体积．20. 已知△BCD 中，∠BCD ＝90°，BC ＝CD ＝1，AB ⊥平面BCD ，∠ADB ＝60°，E ，F 分别是AC ，AD 上的动点，且AC AE ＝ADAF＝(0＜＜1)． (1)求证：不论 为何值，总有平面BEF ⊥平面ABC ；(2)当为何值时，平面BEF ⊥平面ACD ？POEC DBA(第17题)D 1C 1B 1A 1CD BA(第19题)(第18题)第三章 直线与方程一、选择题1．下列直线中与直线x －2y ＋1＝0平行的一条是( )． A ．2x －y ＋1＝0 B ．2x －4y ＋2＝0 C ．2x ＋4y ＋1＝0D ．2x －4y ＋1＝02．已知两点A (2，m )与点B (m ，1)之间的距离等于13，则实数m ＝( )． A ．－1B ．4C ．－1或4D ．－4或13．过点M (－2，a )和N (a ，4)的直线的斜率为1，则实数a 的值为( )． A ．1B ．2C ．1或4D ．1或24．如果AB ＞0，BC ＞0，那么直线Ax ―By ―C ＝0不经过的象限是( )． A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．已知等边△ABC 的两个顶点A (0，0)，B (4，0)，且第三个顶点在第四象限，则BC 边所在的直线方程是( )．A ．y ＝－3xB ．y ＝－3(x －4)C ．y ＝3(x －4)D ．y ＝3(x ＋4)6．直线l ：mx －m 2y －1＝0经过点P (2，1)，则倾斜角与直线l 的倾斜角互为补角的一条直线方程是( )．A ．x ―y ―1＝0B ．2x ―y ―3＝0C ．x ＋y －3＝0D ．x ＋2y －4＝07．点P (1，2)关于x 轴和y 轴的对称的点依次是( )． A ．(2，1)，(－1，－2) B ．(－1，2)，(1，－2) C ．(1，－2)，(－1，2)D ．(－1，－2)，(2，1)8．已知两条平行直线l 1 : 3x ＋4y ＋5＝0，l 2 : 6x ＋by ＋c ＝0间的距离为3，则b ＋c ＝( )．A ．－12B ．48C ．36D ．－12或489．过点P (1，2)，且与原点距离最大的直线方程是( )． A ．x ＋2y －5＝0 B ．2x ＋y －4＝0 C ．x ＋3y －7＝0D ．3x ＋y －5＝010．a ，b 满足a ＋2b ＝1，则直线ax ＋3y ＋b ＝0必过定点( )． A ．⎪⎭⎫⎝⎛21 ，61 －B ．⎪⎭⎫ ⎝⎛61 － ，21C ．⎪⎭⎫⎝⎛61 ，21D ．⎪⎭⎫ ⎝⎛21 － ，61二、填空题11．已知直线AB 与直线AC 有相同的斜率，且A (1，0)，B (2，a )，C (a ，1)，则实数a 的值是____________．12．已知直线x －2y ＋2k ＝0与两坐标轴所围成的三角形的面积不大于1，则实数k 的取值范围是____________．13．已知点(a ，2)(a ＞0)到直线x －y ＋3＝0的距离为1，则a 的值为________． 14．已知直线ax ＋y ＋a ＋2＝0恒经过一个定点，则过这一定点和原点的直线方程是 ____________________．15．已知实数x ，y 满足5x ＋12y ＝60，则22 ＋ y x 的最小值等于____________． 三、解答题 16．求斜率为43，且与坐标轴所围成的三角形的周长是12的直线方程． 17．过点P (1，2)的直线l 被两平行线l 1 : 4x ＋3y ＋1＝0与l 2 : 4x ＋3y ＋6＝0截得的线段长|AB |＝2，求直线l 的方程．18．已知方程(m 2―2m ―3)x ＋(2m 2＋m －1)y ＋6－2m ＝0(m ∈R )． (1)求该方程表示一条直线的条件；(2)当m 为何实数时，方程表示的直线斜率不存在？求出这时的直线方程； (3)已知方程表示的直线l 在x 轴上的截距为－3，求实数m 的值； (4)若方程表示的直线l 的倾斜角是45°，求实数m 的值．19．△ABC 中，已知C (2，5)，角A 的平分线所在的直线方程是y ＝x ，BC 边上高线所在的直线方程是y ＝2x －1，试求顶点B 的坐标．第四章 圆与方程一、选择题1．圆C 1 : x 2＋y 2＋2x ＋8y －8＝0与圆C 2 : x 2＋y 2－4x ＋4y －2＝0的位置关系是( )． A ．相交B ．外切C ．内切D ．相离2．两圆x 2＋y 2－4x ＋2y ＋1＝0与x 2＋y 2＋4x －4y －1＝0的公共切线有( )． A ．1条B ．2条C ．3条D ．4条3．若圆C 与圆(x ＋2)2＋(y －1)2＝1关于原点对称，则圆C 的方程是( )． A ．(x －2)2＋(y ＋1)2＝1 B ．(x －2)2＋(y －1)2＝1 C ．(x －1)2＋(y ＋2)2＝1D ．(x ＋1)2＋(y －2)2＝14．与直线l : y ＝2x ＋3平行，且与圆x 2＋y 2－2x －4y ＋4＝0相切的直线方程是( )． A ．x －y ±5＝0 B ．2x －y ＋5＝0 C ．2x －y －5＝0D ．2x －y ±5＝05．直线x －y ＋4＝0被圆x 2＋y 2＋4x －4y ＋6＝0截得的弦长等于( )． A ．2B ．2C ．22D ．426．一圆过圆x 2＋y 2－2x ＝0与直线x ＋2y －3＝0的交点，且圆心在y 轴上，则这个圆的方程是( )．A ．x 2＋y 2＋4y －6＝0B ．x 2＋y 2＋4x －6＝0C ．x 2＋y 2－2y ＝0D ．x 2＋y 2＋4y ＋6＝07．圆x 2＋y 2－4x －4y －10＝0上的点到直线x ＋y －14＝0的最大距离与最小距离的差是( )．A ．30B ．18C ．62D ．528．两圆(x －a )2＋(y －b )2＝r 2和(x －b )2＋(y －a )2＝r 2相切，则( )． A ．(a －b )2＝r 2 B ．(a －b )2＝2r 2 C ．(a ＋b )2＝r 2D ．(a ＋b )2＝2r 29．若直线3x －y ＋c ＝0，向右平移1个单位长度再向下平移1个单位，平移后与圆x 2＋y 2＝10相切，则c 的值为( )．A ．14或－6B ．12或－8C ．8或－12D ．6或－1410．设A (3，3，1)，B (1，0，5)，C (0，1，0)，则AB 的中点M 到点C 的距离|CM | ＝( )．A ．453B ．253 C ．253 D ．213二、填空题11．若直线3x －4y ＋12＝0与两坐标轴的交点为A ，B ，则以线段AB 为直径的圆的一般方程为____________________．12．已知直线x ＝a 与圆(x －1)2＋y 2＝1相切，则a 的值是_________． 13．直线x ＝0被圆x 2＋y 2―6x ―2y ―15＝0所截得的弦长为_________． 14．若A (4，－7，1)，B (6，2，z )，|AB |＝11，则z ＝_______________．15．已知P 是直线3x ＋4y ＋8＝0上的动点，P A ，PB 是圆(x －1)2＋(y －1)2＝1的两条切线，A ，B 是切点，C 是圆心，则四边形P ACB 面积的最小值为 ．三、解答题16．求下列各圆的标准方程：(1)圆心在直线y ＝0上，且圆过两点A (1，4)，B (3，2)；(2)圆心在直线2x ＋y ＝0上，且圆与直线x ＋y －1＝0切于点M (2，－1)．17．棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 是AB 的中点，F 是BB 1的中点，G 是不抛弃，不放弃。

必修2立体几何证明题详解（五篇）第一篇：必修2 立体几何证明题详解迎接新的挑战!必修2 证明题一．解答题（共3小题）1．（2006•北京）如图，在底面为平行四边形的四棱锥P﹣ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．（1）求证：PB∥平面AEC；（2）求二面角E﹣AC﹣B的大小．考点：三垂线定理；直线与平面平行的判定。

分析：（1）欲证PB∥平面AEC，根据直线与平面平行的判定定理可知只需证PB与平面AEC内一直线平行即可，连BD交AC于点O，连EO，则EO是△PDB的中位线则EO∥PB，满足条件；（2）取AD的中点F，连EF，FO，根据定义可知∠EOF是二面角E﹣AC﹣D的平面角，在△EOF中求出此角，而二面角E﹣AC﹣B与二面角E﹣AC﹣D互补．解答：解：（1）由PA⊥平面ABCD可得PAAC又AB⊥AC，所以AC⊥平面PAB，所以AC⊥PB连BD交AC于点O，连EO，则EO是△PDB的中位线，∴EO∥PB ∴PB∥平面AEC（2）取AD的中点F，连EF，FO，则EF是△PAD的中位线，∴EF∥PA又PA⊥平面ABCD，∴EF⊥平面ABCD同理FO是△ADC的中位线，∴FO∥AB，FO⊥AC由三垂线定理可知∠EOF是二面角E﹣AC﹣D的平面角．又FO=AB=PA=EF∴∠EOF=45°而二面角E﹣AC﹣B与二面角E﹣AC﹣D互补，故所求二面角E﹣AC﹣B的大小为135°．点评：本题主要考查了直线与平面平行的判定，以及二面角等有关知识，考查空间想象能力、运算能力和推理论证能力，属于基础题．2．如图，已知∠BAC在平面α内，P∉α，∠PAB=∠PAC，求证：点P在平面α上的射影在∠BAC的平分线上．考点：三垂线定理。

专题：作图题；证明题。

分析：作PO⊥α，PE⊥AB，PF⊥AC，垂足分别为O，E，F，连接OE，OF，OA，证明Rt△AOE≌Rt△AOF，然后得到点P在平面α上的射影在∠BAC的平分线上．解答：证明：作PO⊥α，PE⊥AB，PF⊥AC，垂足分别为O，E，F，连接OE，OF，OA，∵⇒Rt△PAE≌Rt△PAF⇒AE=AF，∵，又∵AB⊥PE，∴AB⊥平面PEO，∴AB⊥OE，同理AC⊥OF．欢迎加入高一数学组联系电话:***迎接新的挑战!必修2 证明题在Rt△AOE和Rt△AOF，AE=AF，OA=OA，∴Rt△AOE≌Rt△AOF，∴∠EAO=∠FAO，即点P在平面α上的射影在∠BAC的平分线上．点评：本题考查三垂线定理，考查学生逻辑思维能力，是基础题．3．已知正四棱柱ABCD﹣A1B1C1D1中，AB=2，AA1=3．（I）求证：A1C⊥BD；（II）求直线A1C与侧面BB1C1C所成的角的正切值；（III）求二面角B1﹣CD﹣B的正切值．考点：三垂线定理；直线与平面所成的角；与二面角有关的立体几何综合题。

高中数学立体几何经典常考题型题型一:空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明，一般出现在解答题的第(1)问，解答题的第(2)问常考查求空间角，求空间角一般都可以建立空间直角坐标系，用空间向量的坐标运算求解.【例1】如图，在△ABC中，∠ABC＝，O为AB边上一点，且3OB＝3OC＝2AB，已知PO⊥平面ABC，2DA＝2AO＝PO，且DA∥PO.(1)求证：平面PBD⊥平面COD；(2)求直线PD与平面BDC所成角的正弦值.(1)证明　∵OB＝OC，又∵∠ABC＝，∴∠OCB＝，∴∠BOC＝.⊥∴CO AB.又PO⊥平面ABC，⊥OC⊂平面ABC，∴PO OC.又∵PO，AB⊂平面PAB，PO∩AB＝O，∴CO⊥平面PAB，即CO⊥平面PDB.又CO⊂平面COD，∴平面PDB⊥平面COD.(2)解　以OC，OB，OP所在射线分别为x，y，z轴，建立空间直角坐标系，如图所示.设OA＝1，则PO＝OB＝OC＝2，DA＝1.则C(2，0，0)，B(0，2，0)，P(0，0，2)，D(0，－1，1)，∴PD＝(0，－1，－1)，BC＝(2，－2，0)，BD＝(0，－3，1).设平面BDC的一个法向量为n＝(x，y，z)，∴∴令y＝1，则x＝1，z＝3，∴n＝(1，1，3).设PD与平面BDC所成的角为θ，则sin θ＝＝＝.即直线PD与平面BDC所成角的正弦值为.【类题通法】利用向量求空间角的步骤间标.第一步：建立空直角坐系第二步：确定点的坐标.线)坐标.第三步：求向量(直的方向向量、平面的法向量计夹(或函数值).第四步：算向量的角将夹转为间.第五步：向量角化所求的空角查关键错题规.第六步：反思回顾.看点、易点和答范【变式训练】 如图所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于F.(1)证明：EF∥B1C.(2)求二面角EA1DB1的余弦值.(1)证明　由正方形的性质可知A1B1AB DC∥∥，且A1B1＝AB＝DC，所以四边形A1B1CD为平行四边形，从而B1C A∥1D，又A1D⊂面A1DE，B1C⊄面A1DE，于是B1C∥面A1DE.又B1C⊂面B1CD1，面A1DE∩面B1CD1＝EF，所以EF∥B1C.(2)解　因为四边形AA1B1B，ADD1A1，ABCD均为正方形，所以AA1⊥AB，AA1⊥AD，AB⊥AD且AA1＝AB＝AD.以A为原点，分别以AB，AD，AA1为x轴，y轴和z轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A(0，0，0)，B(1，0，0)，D(0，1，0)，A1(0，0，1)，B1(1，0，1)，D1(0，1，1)，而E点为B1D1的中点，所以E点的坐标为.设平面A1DE的一个法向量n1＝(r1，s1，t1)，而该面上向量A1E＝，A1D＝(0，1，－1)，由n1⊥A1E，n1⊥A1D得r1，s1，t1应满足的方程组(－1，1，1)为其一组解，所以可取n1＝(－1，1，1).设平面A1B1CD的一个法向量n2＝(r2，s2，t2)，而该面上向量A1B1＝(1，0，0)，A1D＝(0，1，－1)，由此同理可得n2＝(0，1，1).所以结合图形知二面角EA1DB1的余弦值为＝＝.题型二:立体几何中的探索性问题此类试题一般以解答题形式呈现，常涉及线、面平行、垂直位置关系的探究或空间角的计算问题，是高考命题的热点，一般有两种解决方式：(1)根据条件作出判断，再进一步论证；(2)利用空间向量，先假设存在点的坐标，再根据条件判断该点的坐标是否存在.【例2】如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，AB⊥AD，AB＝1，AD＝2，AC＝CD＝.(1)求证：PD⊥平面PAB；(2)求直线PB与平面PCD所成角的正弦值；(3)在棱PA上是否存在点M，使得BM∥平面PCD？若存在，求的值；若不存在，说明理由.(1)证明　因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，AB⊥AD，所以AB⊥平面PAD，所以AB⊥PD.又PA⊥PD，AB∩PA＝A，所以PD⊥平面PAB.(2)解　取AD的中点O，连接PO，CO.因为PA＝PD，所以PO⊥AD.因为PO⊂平面PAD，平面PAD⊥平面ABCD，所以PO⊥平面ABCD.因为CO⊂平面ABCD，所以PO⊥CO.因为AC＝CD，所以CO⊥AD.如图，建立空间直角坐标系O－xyz.由题意得，A(0，1，0)，B(1，1，0)，C(2，0，0)，D(0，－1，0)，P(0，0，1).设平面PCD的一个法向量为n＝(x，y，z)，则即令z＝2，则x＝1，y＝－2.所以n＝(1，－2，2).又PB＝(1，1，－1)，所以cos〈n，PB〉＝＝－.所以直线PB与平面PCD所成角的正弦值为.(3)解　设M是棱P A上一点，则存在λ∈0，1]，使得AM＝λAP.因此点M(0，1－λ，λ)，BM＝(－1，－λ，λ).因为BM⊄平面PCD，所以要使BM∥平面PCD，则BM·n＝0，即(－1，－λ，λ)·(1，－2，2)＝0，解得λ＝.所以在棱P A上存在点M，使得BM∥平面PCD，此时＝.应设，把要成立的作件结论当条，据此列方对断问题，先假存在【类题通法】(1)于存在判型的求解规围内”等.标，是否有定范的解程或方程组，把“是否存在”化问题转为“点的坐是否有解对问题，通常借助向量，引进参数，合已知和列出等式综结论，解出参数.(2)于位置探究型【变式训练】如图，在四棱锥P－ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，DC＝6，AD＝8，BC＝10，∠P AD＝45°，E为P A的中点.(1)求证：DE∥平面BPC；(2)线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出二面角F－PC－D的余弦值；若不存在，请说明理由.(1)证明　取PB的中点M，连接EM和CM，过点C作CN⊥AB，垂足为点N.∵CN⊥AB，DA⊥AB，∴CN∥DA，又AB∥CD，∴四边形CDAN为平行四边形，∴CN＝AD＝8，DC＝AN＝6，在Rt△BNC中，BN＝＝＝6，∴AB＝12，而E，M分别为P A，PB的中点，∴EM∥AB且EM＝6，又DC∥AB，∥且EM＝CD，四边形CDEM为平行四边形，∴EM CD∥∵⊂平面PBC，DE⊄平面PBC，∴DE CM.CM∴DE∥平面BPC.(2)解　由题意可得DA，DC，DP两两互相垂直，如图，以D为原点，DA，DC，DP分别为x，y，z轴建立空间直角坐标系D－xyz，则A(8，0，0)，B(8，12，0)，C(0，6，0)，P(0，0，8).假设AB上存在一点F使CF⊥BD，设点F坐标为(8，t，0)，则CF＝(8，t－6，0)，DB＝(8，12，0)，由CF·DB＝0得t＝.又平面DPC的一个法向量为m＝(1，0，0)，设平面FPC的法向量为n＝(x，y，z).又PC＝(0，6，－8)，FC＝.由得即不妨令y＝12，有n＝(8，12，9).则cos〈n，m〉＝＝＝.又由图可知，该二面角为锐二面角，故二面角F－PC－D的余弦值为.题型三:立体几何中的折叠问题将平面图形沿其中一条或几条线段折起，使其成为空间图形，这类问题称为立体几何中的折叠问题，折叠问题常与空间中的平行、垂直以及空间角相结合命题，考查学生的空间想象力和分析问题的能力.【例3】如图，菱形ABCD的对角线AC与BD交于点O，AB＝5，AC＝6，点E，F分别在AD，CD 上，AE＝CF＝，EF交BD于点H.将△DEF沿EF折到△D′EF的位置，OD′＝.(1)证明：D′H⊥平面ABCD；(2)求二面角B－D′A－C的正弦值.(1)证明　由已知得AC ⊥BD ，AD ＝CD .又由AE ＝CF 得＝，故AC ∥EF .因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝＝4.由EF ∥AC 得＝＝.所以OH ＝1，D ′H ＝DH ＝3.于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH .又D ′H ⊥EF ，而OH ∩EF ＝H ，所以D ′H ⊥平面ABCD .(2)解　如图，以H 为坐标原点，HF 的方向为x 轴正方向，建立空间直角坐标系H －xyz .则H (0，0，0)，A (－3，－1，0)，B (0，－5，0)，C (3，－1，0)，D ′(0，0，3)，AB ＝(3，－4，0)，AC ＝(6，0，0)，AD′＝(3，1，3).设m ＝(x 1，y 1，z 1)是平面ABD ′的一个法向量，则即所以可取m ＝(4，3，－5).设n ＝(x 2，y 2，z 2)是平面ACD ′的一个法向量，则即所以可取n ＝(0，－3，1).于是cos 〈m ，n 〉＝＝＝－.sin 〈m ，n 〉＝.因此二面角B －D ′A －C 的正弦值是.【类题通法】立体几何中的折叠问题，是翻折前后形中面位置系和度量系的化关键搞清图线关关变情况，一般地翻折后在同一平面上的性不生化还个质发变，不在同一平面上的性生化个质发变.【变式训练】如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置，如图2.(1)证明：CD⊥平面A1OC；(2)若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD夹角的余弦值.(1)证明　在题图1中，因为AB＝BC＝1，AD＝2，E是AD的中点，∠BAD＝，所以BE⊥AC.即在题图2中，BE⊥OA1，BE⊥OC，从而BE⊥平面A1OC.又CD∥BE，所以CD⊥平面A1OC.(2)解　由已知，平面A1BE⊥平面BCDE，又由(1)知，BE⊥OA1，BE⊥OC，所以∠A1OC为二面角A1－BE－C的平面角，所以∠A1OC＝.如图，以O为原点，OB，OC，OA1分别为x轴、y轴、z轴正方向建立空间直角坐标系，因为A1B＝A1E＝BC＝ED＝1，BC∥ED，所以B，E，A1，C，得BC＝，A1C＝，CD＝BE＝(－，0，0).设平面A1BC的一个法向量n1＝(x1，y1，z1)，平面A1CD的一个法向量n2＝(x2，y2，z2)，平面A1BC与平面A1CD的夹角为θ，则得取n1＝(1，1，1)；得取n2＝(0，1，1)，从而cos θ＝|cos〈n1，n2〉|＝＝，即平面A1BC与平面A1CD夹角的余弦值为.。

必修二空间几何证明经典题型考试围：必修二空间几何；考试时间：100分钟；命题人：罗文波第Ⅰ卷（选择题）请点击修改第I卷的文字说明评卷人得分一．解答题（共25小题）1．如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E 和F分别是CD和PC的中点，求证：（Ⅰ）BE∥平面PAD；（Ⅱ）PA⊥BC；（Ⅲ）平面BEF⊥平面PCD．2．如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC=，O，M分别为AB，VA的中点．（Ⅰ）求证：VB∥平面M OC；（Ⅱ）求证：平面MOC⊥平面VAB ；（Ⅲ）求三棱锥A﹣MOC的体积．3．如图，在三棱锥P﹣ABC中，PA⊥PC，AB=PB，E，F分别是PA，AC的中点．求证：（1）EF∥平面PBC；（2）平面BEF⊥平面PAB．4．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D 不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．5．已知四棱锥A﹣BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥面ABC，BE∥CD，F为AD的中点．（Ⅰ）求证：EF∥面ABC；（Ⅱ）求证：平面ADE⊥平面ACD；（Ⅲ）求四棱锥A﹣BCDE的体积．6．如图，四棱柱ABCD﹣A1B1C1D1中，平面A1ABB1⊥平面ABCD，且∠ABC=．（1）求证：BC∥平面AB 1C1；（2）求证：平面A1ABB1⊥平面AB1C1．7．如图，三角形ABC中，AC=BC=，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD 的中点．（Ⅰ）求证：GF∥底面ABC；（Ⅱ）求证：AC⊥平面EBC；（Ⅲ）求几何体ADEBC的体积V．8．如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E分别是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．9．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，EF=AB，平面BCF⊥平面ABCD，BF=CF，G为BC的中点，求证：（1）OG∥平面ABFE；（2）AC⊥平面BDE．10．如图所示，四棱锥P﹣ABCD的底面为直角梯形，AB⊥AD，CD⊥AD，CD=2AB．点E是PC的中点．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）已知平面PCD⊥底面ABCD，且PC=DC．在棱PD 上是否存在点F，使CF⊥PA？请说明理由．11．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=AD，E、F分别为PC、BD的中点．（1）求证：EF∥平面PAD；（2）求证：面PAB⊥平面PDC．12．在长方体ABCD﹣A1B1C1D1中，AB=BC=EC=．求证：（1）AC1∥平面BDE；（2）A1E⊥平面BDE．13．如图，ACQP所在的平面与菱形ABCD所在的平面相互垂直，交线为AC，若分别是PQ，CQ的中点．求证：（1）CE∥平面PBD；（2）平面FBD⊥平面PBD．14．已知直四棱柱ABCD﹣A1B1C1D1的底面是菱形，F为棱BB1的中点，M为线段AC1的中点．求证：（Ⅰ）直线MF∥平面ABCD；（Ⅱ）平面AFC1⊥平面ACC1A1．15．如图，四棱锥P﹣ABCD中，AD⊥平面PAB，AP⊥AB．（1）求证：CD⊥AP；（2）若CD⊥PD，求证：CD∥平面PAB．16．如图，四棱锥P﹣ABCD的底面是矩形，PA⊥平面ABCD，E，F分别是AB，PD 的中点，且PA=AD．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求证：平面PEC⊥平面PCD．17．如图，三棱柱ABC﹣A1B1C l中，M，N分别为CC1，A1B1的中点．CA⊥CB1，CA=CB1，BA=BC=BB1．（Ⅰ）求证：直线MN∥平面CAB1；（Ⅱ）求证：直线BA1⊥平面CAB1．18．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．（I）求证：EM⊥AD；（II）求证：MN∥平面ADE；（III）求点A到平面BCE的距离．19．在四棱锥P﹣ABCD 中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC⊥PD，E，F分别是PB，BC的中点．求证：（1）PC∥平面DEF；（2）平面PBC⊥平面PBD．20．如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，FD⊥平面ABCD，．（I）求证：EF∥平面ABCD；（II）求证：平面ACF⊥平面BDF．21．如图，在直三棱柱ABC﹣A1B1C 1中，AC⊥BC，A1B与AB1交于点D，A1C与AC1交于点E．求证：（1）DE∥平面B1BCC1；（2）平面A1BC⊥平面A1ACC1．22．如图，在多面体ABCDPE中，四边形ABCD和CDPE都是直角梯形，AB∥DC，PE∥DC，AD ⊥DC，PD⊥平面ABCD，AB=PD=DA=2PE，CD=3PE，F是CE的中点．（1）求证：BF∥平面ADP（2）已知O是BD的中点，求证：BD⊥平面AOF．23．如图，在几何体ABCDEF中，底面ABCD为矩形，EF ∥CD，CD⊥EA，CD=2EF=2，ED=．M 为棱FC上一点，平面ADM与棱FB交于点N．（Ⅰ）求证：ED⊥CD；（Ⅱ）求证：AD∥MN；（Ⅲ）若AD⊥ED，试问平面BCF是否可能与平面ADMN垂直？若能，求出的值；若不能，说明理由．24．如图，在三棱锥A﹣BCD中，E，F分别为BC，CD上的点，且BD∥平面AEF．（1）求证：EF∥平ABD面；（2）若AE⊥平面BCD，BD⊥CD，求证：平面AEF⊥平面ACD．25．如图，四棱锥P﹣ABCD中，底面ABCD是平行四边形，且平面PAC⊥平面ABCD，E为PD 的中点，PA=PC，AB=2BC=2，∠ABC=60°．（Ⅰ）求证：PB∥平面ACE；（Ⅱ）求证：平面PBC⊥平面PAC．必修二空间几何证明经典题型一．解答题（共25小题）1．如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E 和F分别是CD和PC的中点，求证：（Ⅰ）BE∥平面PAD；（Ⅱ）PA⊥BC；（Ⅲ）平面BEF⊥平面PCD．【解答】解：（Ⅰ）∵PA⊥AD，平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，由平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅱ）∵AB∥CD，AB⊥AD，CD=2AB，E和F分别是CD和PC的中点，故四边形ABED为平行四边形，故有BE∥AD．又AD⊂平面PAD，BE不在平面PAD，故有BE∥平面PAD．（Ⅲ）平行四边形ABED中，由AB⊥AD可得，ABED为矩形，故有BE⊥CD．由PA⊥平面ABCD，可得PA⊥AB，再由AB⊥AD可得AB⊥平面PAD，∴CD⊥平面PAD，故有CD⊥PD．再由E、F分别为CD和PC的中点，可得EF∥PD，∴CD⊥EF．而EF和BE是平面BEF的两条相交直线，故有CD⊥平面BEF．由于CD⊂平面PCD，∴平面BEF⊥平面PCD．2．如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC=，O，M分别为AB，VA的中点．（Ⅰ）求证：VB∥平面M OC；（Ⅱ）求证：平面MOC⊥平面VAB；（Ⅲ）求三棱锥A﹣MOC的体积．【解答】（Ⅰ）证明：∵O，M分别为AB，VA的中点，∴OM∥VB，∵VB⊄平面MOC，OM⊂平面MOC，∴VB∥平面MOC；（Ⅱ）证明：∵AC=BC，O为AB的中点，∴OC⊥AB，又∵平面VAB⊥平面ABC，平面ABC ∩平面VAB=AB，且OC⊂平面ABC，∴OC⊥平面VAB，∵OC⊂平面MOC，∴平面MOC⊥平面VAB；（Ⅲ）解：在等腰直角三角形ACB中，AC=BC=，∴AB=2，OC=1，∴等边三角形VAB的边长为2，S△VAB=，∵O，M分别为AB，VA的中点．∴．又∵OC⊥平面VAB，∴三棱锥．3．如图，在三棱锥P﹣ABC中，PA⊥PC，AB=PB，E，F分别是PA，AC的中点．求证：（1）EF∥平面PBC；（2）平面BEF⊥平面PAB．【解答】证明：（1）在△APC中，因为E、F分别是PA、AC的中点，所以EF∥PC，…（3分）又PC⊂平面PAC，EF⊄平面PAC，所以EF∥平面PBC．…（6分）（2）因为AB=PB，且点E是PA的中点，所以PA⊥BE，…（9分）又PA⊥PC，EF∥PC，所以PA⊥EF ，…（12分）因为BE⊂平面BEF，EF⊂平面BEF，BE∩EF=E，所以PA⊥平面BEF，又PA⊂平面PAB，所以平面PAB⊥平面BEF．…（14分）4．如图，在三棱锥A﹣BCD中，AB⊥AD，BC ⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D 不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊂平面ABC，AB⊂平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．5．已知四棱锥A﹣BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥面ABC，BE∥CD，F为AD的中点．（Ⅰ）求证：EF∥面ABC；（Ⅱ）求证：平面ADE⊥平面ACD；（Ⅲ）求四棱锥A﹣BCDE的体积．【解答】证明：（Ⅰ）取AC 中点G ，连接FG 、BG ， ∵F ，G 分别是AD ，AC 的中点 ∴FG ∥CD ，且FG=DC=1． ∵BE ∥CD ∴FG 与BE 平行且相等 ∴EF ∥BG ． EF ⊄面ABC ，BG ⊂面ABC ∴EF ∥面ABC…（4分）（Ⅱ）∵△ABC 为等边三角形∴BG ⊥AC 又∵DC ⊥面ABC ，BG ⊂面ABC ∴DC ⊥BG ∴BG 垂直于面ADC 的两条相交直线AC ，DC ，∴BG ⊥面ADC ． …（6分） ∵EF ∥BG ∴EF ⊥面ADC∵EF ⊂面ADE ，∴面ADE ⊥面ADC ． …（8分） 解：（Ⅲ）方法一：连接EC ，该四棱锥分为两个三棱锥E ﹣ABC 和E ﹣ADC ．．…（12分）方法二：取BC 的中点为O ，连接AO ，则AO ⊥BC ，又CD ⊥平面ABC ， ∴CD ⊥AO ，BC ∩CD=C ，∴AO ⊥平面BCDE ， ∴AO 为V A ﹣BCDE的高，，∴．6．如图，四棱柱ABCD ﹣A 1B 1C 1D 1中，平面A 1ABB 1⊥平面ABCD ，且∠ABC=．（1）求证：BC ∥平面AB 1C 1；（2）求证：平面A 1ABB 1⊥平面AB 1C 1．【解答】证明：（1）∵BC ∥B 1C 1，且B 1C 1⊂平面AB 1C 1，BC ⊄平面AB 1C 1， ∴BC ∥平面AB 1C 1．（2）∵平面A 1ABB 1⊥平面ABCD ，平面ABCD ∥平面A 1B 1C 1D 1， ∴平面A 1ABB 1⊥平面A 1B 1C 1D 1，∵平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1，A 1B 1⊥C 1B 1， ∴C 1B 1⊂平面AB 1C 1， ∴平面A 1ABB 1⊥平面AB 1C 1．7．如图，三角形ABC中，AC=BC=，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．（Ⅰ）求证：GF∥底面ABC；（Ⅱ）求证：AC⊥平面EBC；（Ⅲ）求几何体ADEBC的体积V．【解答】解：（I）证法一：取BE 的中点H，连接HF、GH，（如图）∵G、F分别是EC和BD的中点∴HG∥BC，HF∥DE，（2分）又∵ADEB为正方形∴DE∥AB，从而HF∥AB∴HF∥平面ABC，HG∥平面ABC，HF∩HG=H，∴平面HGF∥平面ABC∴GF∥平面ABC（5分）证法二：取BC的中点M，AB 的中点N连接GM、FN、MN（如图）∵G、F分别是EC和BD的中点∴（2分）又∵ADEB为正方形∴BE∥AD，BE=AD∴GM∥NF且GM=NF∴MNFG为平行四边形∴GF∥MN，又MN⊂平面ABC，∴GF∥平面ABC（5分）证法三：连接AE，∵ADEB为正方形，∴AE∩BD=F，且F是AE中点，（2分）∴GF∥AC，又AC⊂平面ABC，∴GF∥平面ABC（5分）（Ⅱ）∵ADEB为正方形，∴EB⊥AB，∴GF∥平面ABC（5分）又∵平面ABED⊥平面ABC，∴BE⊥平面ABC（7分）∴BE⊥AC又∵CA2+CB2=AB2∴AC⊥BC，∵BC∩BE=B，∴AC⊥平面BCE（9分）（Ⅲ）连接CN，因为AC=BC，∴CN⊥AB，（10分）又平面ABED⊥平面ABC，CN⊂平面ABC，∴CN⊥平面ABED．（11分）∵三角形ABC是等腰直角三角形，∴，（12分）∵C﹣ABED是四棱锥，∴V C﹣ABED==（14分）8．如图，在直三棱柱ABC﹣A1B1C1中，BC⊥AC，D，E分别是AB，AC的中点．（1）求证：B1C1∥平面A1DE；（2）求证：平面A1DE⊥平面ACC1A1．【解答】证明：（1）因为D，E分别是AB，AC的中点，所以DE∥BC，…（2分）又因为在三棱柱ABC﹣A1B1C1中，B1C1∥BC，所以B1C1∥DE…（4分）又B1C1⊄平面A1DE，DE⊂平面A1DE，所以B1C1∥平面A1DE…（6分）（2）在直三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，又DE⊂底面ABC，所以CC1⊥DE…（8分）又BC⊥AC，DE∥BC，所以DE⊥AC，…（10分）又CC1，AC⊂平面ACC1A1，且CC1∩AC=C，所以DE⊥平面ACC1A1…（12分）又DE⊂平面A1DE，所以平面A1DE⊥平面ACC1A1…（14分）9．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD 相交于点O，EF∥AB，EF=AB，平面BCF⊥平面ABCD，BF=CF，G为BC的中点，求证：（1）OG∥平面ABFE；（2）AC⊥平面BDE．【解答】证明：（1）∵四边形ABCD是菱形，AC，BD相交于点O，∴O是AC中点，∵G为BC的中点，∴OG∥AB，∵OG⊄平面ABFE，AB⊂平面ABFE，∴OG∥平面ABFE．（2）∵四边形ABCD是菱形，AC，BD相交于点O，∴AC⊥BD，O是AC中点，∵G为BC的中点，∵EF∥AB，EF=AB，平面BCF⊥平面ABCD，BF=CF，∴FG⊥平面ABCD，∴EO⊥平面ABCD，∴EO⊥AC，∵EO∩BD=O，∴AC⊥平面BDE．10．如图所示，四棱锥P﹣ABCD的底面为直角梯形，AB⊥AD，CD⊥AD，CD=2AB．点E是PC 的中点．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）已知平面PCD⊥底面ABCD，且PC=DC．在棱PD上是否存在点F，使CF⊥PA？请说明理由．【解答】（1）证明：取PD中点Q，连结AQ、EQ．…（1分）∵E为PC的中点，∴EQ∥CD且EQ=CD．…（2分）又∵AB∥CD且AB=CD，∴EQ∥AB且EQ=AB．…（3分）∴四边形ABED是平行四边形，∴BE∥AQ．…（4分）又∵BE⊄平面PAD，AQ⊂平面PAD，∴BE∥平面PAD．…（5分）（2）解：棱PD上存在点F为PD的中点，使CF⊥PA，∵平面PCD⊥底面ABCD，平面PCD∩底面ABCD=CD，AD⊥CD，∴AD⊥平面PCD，∴DP是PA在平面PCD中的射影，∴PC=DC，PF=DF，∴CF⊥DP，∴CF⊥PA．11．如图，在四棱锥P ﹣ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=AD，E、F分别为PC、BD的中点．（1）求证：EF∥平面PAD；（2）求证：面PAB⊥平面PDC．【解答】证明：（1）连接AC，由正方形性质可知，AC与BD相交于BD的中点F，F也为AC中点，E为PC中点．所以在△CPA中，EF∥PA，又PA⊂平面PAD，EF⊄平面PAD，所以EF∥平面PAD；（2）平面PAD⊥平面ABCD平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA正方形ABCD中CD⊥ADPA⊂平面PADCD⊂平面ABCD又，所以PA2+PD2=AD2所以△PAD是等腰直角三角形，且，即PA⊥PD．因为CD∩PD=D，且CD、PD⊂面PDC所以PA⊥面PDC又PA⊂面PAB，所以面PAB⊥面PDC．12．在长方体ABCD﹣A1B1C1D1中，AB=BC=EC=．求证：（1）AC1∥平面BDE；（2）A1E⊥平面BDE．【解答】解：（1）ABCD﹣A1B1C1D1是长方体，AB=BC=EC=．可得平面ABCD和平面A1B1C1D1是正方形，E为CC1的中点．连接AC与DB交于O，连接OE，可得：AC1∥OE，OE⊂平面BDE．∴AC1∥平面BDE．（2）连接OA1，根据三垂线定理，可得OA1⊥DB，OE⊥DB，OA1∩OE=O，∴平面A1OE⊥DB．可得A 1E⊥DB ．∵E为CC 1的中点．设AB=BC=EC=AA1=a∴，A1E=，A1B=∵A1B2=A1E2+BE2．∴A1E⊥EB．∵EB⊂平面BDE ．BD⊂平面BDE．EB∩BD=B，∴A 1E⊥平面BDE．13．如图，ACQP所在的平面与菱形ABCD所在的平面相互垂直，交线为AC，若分别是PQ ，CQ的中点．求证：（1）CE∥平面PBD；（2）平面FBD⊥平面PBD．【解答】证明：（1）设AC∩BD=O，连接PO，则∵O是AC的中点，E是PQ的中点，∴PE=OC，PE∥OC，∴四边形POCE是平行四边形，∴CE∥PO，∵CE⊄平面PBD，PO⊂平面PBD，∴CE∥平面PBD；（2）∵平面ACQP⊥平面ABCD，平面ACQP∩平面ABCD=AC，BD⊥AC，∴BD⊥平面ACQP，∵PO⊂平面ACQP，∴BD⊥PO，连接AQ，OF，则由三角形相似可AQ⊥PO，∵F是CQ中点，O是AC的中点，∴OF∥AQ，∴OF⊥PO，∵BD∩OF=O，∴PO⊥平面FBD，∵PO⊂平面PBD，∴平面FBD⊥平面PBD．14．已知直四棱柱ABCD﹣A1B1C1D1的底面是菱形，F为棱BB1的中点，M为线段AC1的中点．求证：（Ⅰ）直线MF∥平面ABCD；（Ⅱ）平面AFC1⊥平面ACC1A1．【解答】（本小题满分12分）证明：（Ⅰ）延长C1F交CB的延长线于点N，连接AN．因为F是BB1的中点，所以，F为C1N的中点，B为CN的中点．又M是线段AC1的中点，故MF∥AN．又MF不在平面ABCD，AN⊂平面ABCD，∴MF∥平面ABCD．（Ⅱ）连BD，由直四棱柱ABCD﹣A1B1C1D1 ，可知A1A⊥平面ABCD，又∵BD⊂平面ABCD，∴A1A⊥BD．∵四边形ABCD为菱形，∴AC⊥BD．又∵AC∩A1A=A，AC，A1A⊂平面ACC1A1，∴BD⊥平面ACC1A1．在四边形DANB中，DA∥BN且DA=BN，所以四边形DANB为平行四边形，故NA∥BD，∴NA⊥平面ACC1A1，又因为NA⊂平面AFC1，∴平面AFC1⊥ACC1A1．15．如图，四棱锥P﹣ABCD中，AD⊥平面PAB，AP⊥AB．（1）求证：CD⊥AP；（2）若CD⊥PD，求证：CD∥平面PAB．【解答】（本小题满分14分）证明：（1）因为AD⊥平面PAB，AP⊂平面PAB，所以AD⊥AP．…（2分）又因为AP⊥AB，AB∩AD=A，AB⊂平面ABCD，AD⊂平面ABCD，所以AP⊥平面ABCD．…（4分）因为CD⊂平面ABCD，所以CD⊥AP．…（6分）（2）因为CD⊥AP，CD⊥PD，且PD∩AP=P，PD⊂平面PAD，AP⊂平面PAD，所以CD⊥平面PAD．①…（8分）因为AD⊥平面PAB，AB⊂平面PAB，所以AB⊥AD．又因为AP⊥AB，AP∩AD=A，AP⊂平面PAD，AD⊂平面PAD，所以AB⊥平面PAD．②…（10分）由①②得CD∥AB，…（12分）因为CD ⊄平面PAB ，AB ⊂平面PAB ，所以CD ∥平面PAB ．…（14分）16．如图，四棱锥P ﹣ABCD 的底面是矩形，PA ⊥平面ABCD ，E ，F 分别是AB ，PD 的中点，且PA=AD ．（Ⅰ）求证：AF ∥平面PEC ； （Ⅱ）求证：平面PEC ⊥平面PCD ．【解答】证明：（Ⅰ）取PC 的中点G ，连结FG 、EG ， ∴FG 为△CDP 的中位线，FG ∥CD ，FG=CD ．∵四边形ABCD 为矩形，E 为AB 的中点，∴AE ∥CD ，AE=CD ． ∴FG=AE ，FG ∥AE ，∴四边形AEGF 是平行四边形， ∴AF ∥EG 又EG ⊂平面PCE ，AF ⊄平面PCE ， ∴AF ∥平面PCE ； （Ⅱ）∵PA=AD ．∴AF ⊥PD PA ⊥平面ABCD ，∴PA ⊥CD ，又因为CD ⊥AB ，AP ∩AB=A ，∴CD ⊥面APD ∴CD ⊥AF ，且PD ∩CD=D ，∴AF ⊥面PDC 由（Ⅰ）得EG ∥AF ，∴EG ⊥面PDC又EG ⊂平面PCE ，∴平面PEC ⊥平面PCD ．17．如图，三棱柱ABC ﹣A 1B 1C l 中，M ，N 分别为CC 1，A 1B 1的中点．CA ⊥CB 1，CA=CB 1，BA=BC=BB 1． （Ⅰ）求证：直线MN ∥平面CAB 1； （Ⅱ）求证：直线BA 1⊥平面CAB 1．【解答】证明：（Ⅰ）设A 1B 与AB 1交于点O ，连接CO ，ON ．因为四边形ABB 1A 1是平行四边形，所以是O 是AB 1的中点，又N 是A 1B 1的中点，所以．ON又因为M 是CC 1的中点，所以．所以四边形CMNO 是平行四边形，所以MN ∥CO ． 又因为MN ⊄平面CAB 1，CO ⊂CAB 1平面， 所以直线NM ∥平面CAB 1．…（6分）（Ⅱ）因为BA=BB 1，所以平行四边形ABB 1A 1是菱形，所以BA 1⊥AB 1． 因为CA=CB 1，O 是AB 1的中点，所以CO ⊥AB 1， 又CA ⊥CB 1，∴CO=AO ．又因为BA=BC ，所以△BOC ≌△BOA ，所以∠BOC=∠BOA ，故BO ⊥CO ，即BA 1⊥CO ． 又AB 1∩CO=O ，AB 1⊂平面CAB 1，CO ⊂平面CAB 1， 所以直线BA 1⊥平面CAB 1．…（12分）18．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．（I）求证：EM⊥AD；（II）求证：MN∥平面ADE；（III ）求点A到平面BCE的距离．【解答】证明：（Ⅰ）∵EA=EB，M是AB的中点，∴EM⊥AB，（1分）∵平面ABE⊥平面ABCD，平面ABE∩平面ABCD=AB，EM⊂平面ABE，∴EM⊥平面ABCD，（4分）∵AD⊂平面ABCD，∴EM⊥AD．（5分）（Ⅱ）取DE的中点F，连接AF，NF，∵N 是CE的中点．，∴NF CD，∵M是AB的中点，∴AM，∴NF AM，∴四边形AMNF是平行四边形，（7分）∴MN∥AF，（8分）∵MN⊄平面ADE，AF⊂平面ADE，∴MN∥平面ADE．（10分）解：（III）设点A到平面BCE的距离为d，由（I）知ME ⊥平面ABC，BC=BE=2，MC=ME=，则CE=，BN==，（12分）∴，=，∵V A﹣BCE=V E﹣ABC，（13分）即，解得d=，故点A到平面BCE 的距离为．（14分）19．在四棱锥P﹣ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC⊥PD，E，F分别是PB，BC的中点．求证：（1）PC∥平面DEF；（2）平面PBC⊥平面PBD．【解答】证明：（1）∵E，F分别是PB，BC的中点，∴PC∥EF，又PC⊄平面DEF，EF⊂平面DEF，∴PC∥平面DEF．（2）取CD的中点M ，连结BM，则AB DM，又AD⊥AB，AB=AD，∴四边形ABMD是正方形，∴BM⊥CD，BM=CM=DM=1，BD=，∴BC=，∴BD2+BC2=CD2，∴BC⊥BD，又BC⊥PD，BD∩PD=D，∴BC⊥平面PBD，又BC⊂平面PBC，∴平面PBC⊥平面PBD．20．如图，菱形ABCD 与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，FD⊥平面ABCD，．（I ）求证：EF∥平面ABCD；（II）求证：平面ACF⊥平面BDF．【解答】证明：（Ⅰ）如图，过点E作EH⊥BC于H，连接HD，∴．∵平面ABCD⊥平面BCE，EH⊂平面BCE，平面ABCD∩平面BCE=BC，∴EH⊥平面ABCD，又∵FD⊥平面ABCD，，∴FD∥EH，FD=EH．∴四边形EHDF为平行四边形．∴EF∥HD．∵EF⊄平面ABCD，HD⊂平面ABCD，∴EF∥平面ABCD．…（7分）（Ⅱ）∵FD⊥面ABCD，∴FD⊥AC，又四边形ABCD是菱形，∴AC⊥BD，又FD∩BD=D，∴AC⊥面FBD，又AC⊂面ACF，从而面ACF⊥面BDF．…（12分）21．如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，A1B与AB1交于点D，A1C与AC1交于点E．求证：（1）DE∥平面B1BCC1；（2）平面A1BC⊥平面A1ACC1．【解答】证明：（1）由题意，D，E分别为A1B，A1C的中点，∴DE∥BC，∵DE⊄平面B1BCC1，BC⊂平面B1BCC1，∴DE∥平面B1BCC1；（2）∵AA1⊥平面ABC，BC⊂平面ABC，∴AA1⊥BC，∵AC⊥BC，AC∩AA1=A，∴BC⊥平面A1ACC1，∵BC⊂平面A1BC，∴平面A 1BC ⊥平面A 1ACC 1．22．如图，在多面体ABCDPE 中，四边形ABCD 和CDPE 都是直角梯形，AB ∥DC ，PE ∥DC ，AD ⊥DC ，PD ⊥平面ABCD ，AB=PD=DA=2PE ，CD=3PE ，F 是CE 的中点． （1）求证：BF ∥平面ADP（2）已知O 是BD 的中点，求证：BD ⊥平面AOF ．【解答】证明：（1）作FM ⊥CD ，垂足为M ，连接BM ，则DM=2PE=AB ，EM ∥PD ∵DM ∥AB ，∴DMBA 是平行四边形， ∴BM ∥AD ，∵BM ⊄平面ADP ，AD ⊂平面ADP ∴BM ∥平面ADP 同理EM ∥平面ADP ∵BM ∩EM=M ． ∴平面BFM ∥平面ADP ∵BF ⊂平面BFM ， ∴BF ∥平面ADP ；（2）由（1）可知FM=PE ，DM=BM=2PE ，∴FD=FB=PE ，∵O 是BD 的中点，∴FO ⊥BD ，∵AD=AB ，O 是BD 的中点，∴AO ⊥BD ，∵AO ∩FO=O ， ∴BD ⊥平面AOF ．23．如图，在几何体ABCDEF 中，底面ABCD 为矩形，EF ∥CD ，CD ⊥EA ，CD=2EF=2，ED=．M为棱FC 上一点，平面ADM 与棱FB 交于点N ． （Ⅰ）求证：ED ⊥CD ； （Ⅱ）求证：AD ∥MN ；（Ⅲ）若AD ⊥ED ，试问平面BCF 是否可能与平面ADMN 垂直？若能，求出的值；若不能，说明理由．【解答】（Ⅰ）证明：因为ABCD 为矩形，所以VD ⊥AD ．[（1分）] 又因为CD ⊥EA ，[（2分）] 所以CD ⊥平面EAD ．[（3分）] 所以ED ⊥CD ．[（4分）]（Ⅱ）证明：因为ABCD 为矩形，所以AD ∥BC ，[（5分）] 所以AD ∥平面FBC ．[（7分）] 又因为平面ADMN ∩平面FBC=MN ， 所以AD ∥MN ．[（8分）]（Ⅲ）解：平面ADMN 与平面BCF 可以垂直．证明如下：[（9分）] 连接DF ．因为AD ⊥ED ，AD ⊥CD ．ED ∩CD=D ， 所以AD ⊥平面CDEF ．[（10分）]所以AD⊥DM．因为AD∥MN，所以DM⊥MN．[（11分）]因为平面ADMN ∩平面FBC=MN，若使平面ADMN⊥平面BCF，则DM⊥平面BCF，所以DM⊥FC．[（12分）]在梯形CDEF中，因为EF∥CD，DE⊥CD，CD=2EF=2，ED=，所以DF=DC=2．所以若使DM⊥FC能成立，则M为FC的中点．所以=．[（14分）]24．如图，在三棱锥A﹣BCD中，E，F分别为BC，CD上的点，且BD∥平面AEF．（1）求证：EF∥平ABD面；（2）若AE⊥平面BCD，BD⊥CD，求证：平面AEF⊥平面ACD．【解答】证明：（1）∵BD∥平面AEF，BD⊂平面BCD，平面BCD∩平面AEF=EF，∴BD∥EF，又BD⊂平面ABD，EF⊄平面ABD，∴EF∥平ABD面．（2）∵AE⊥平面BCD，CD⊂平面BCD，∴AE⊥CD，由（1）可知BD∥EF，又BD⊥CD，∴EF⊥CD，又AE∩EF=E，AE⊂平面AEF，EF⊂平面AEF，∴CD⊥平面AEF，又CD⊂平面ACD，∴平面AEF⊥平面ACD．25．如图，四棱锥P﹣ABCD中，底面ABCD是平行四边形，且平面PAC⊥平面ABCD，E为PD 的中点，PA=PC，AB=2BC=2，∠ABC=60°．（Ⅰ）求证：PB∥平面ACE；（Ⅱ）求证：平面PBC⊥平面PAC．【解答】证明：（Ⅰ）连接BD，交AC于点O，连接OE，∵底面ABCD是平行四边形，∴O为BD中点，又E为PD中点，∴OE∥PB，又OE⊂平面ACE，PB⊄平面ACE，∴PB∥平面ACE．（Ⅱ）∵PA=PC，O为AC中点，∴PO⊥AC，又平面PAC⊥平面ABCD，平面PAC∩平面ABCD=AC，PO⊂平面PAC，∴PO⊥平面ABCD，又BC⊂平面ABCD，∴PO⊥BC．在△ABC中，AB=2BC=2，∠ABC=60°，∴=，∴AC2=AB2+BC2，∴BC⊥AC．又PO⊂平面PAC，AC⊂平面PAC，PO∩AC=O，∴BC⊥平面PAC，又BC⊂平面PBC，∴平面PBC⊥平面PAC．。

数学必修2第一章一、学习目标：1. 认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构。

2. 能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图与直观图，能识别上述三视图与直观图所表示的立体模型。

二、重点、难点：重点：空间几何体中的棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的结构特征；空间几何体的三视图与直观图的画法。

难点：柱、锥、台、球结构特征的概括；识别三视图所表示的空间几何体；几何体的侧面展开图，计算组合体的表面积和体积。

三、考点分析：三视图是新课程改革中出现的内容，是新课程高考的热点之一，几乎每年都考，同学们要予以足够的重视。

在高考中经常以选择、填空题的形式出现，属于基础或中档题，但也要关注三视图以提供信息为目的，出现在解答题中。

这部分知识主要考查学生的空间想象能力与计算求解能力。

1. 多面体棱柱、棱锥、棱台2. 旋转体圆柱、圆锥、圆台、球3. 三视图（1）正视图、侧视图、俯视图（2）三种视图间的关系4. 直观图水平放置的平面图形的直观图的斜二测画法4.表中S表示面积，c > c分别表示上、下底面的周长，h表示咼度，h表示斜咼，I表示侧棱长。

5. 旋转体的面积和体积公式名称圆柱圆锥圆台球S 侧 2 n rl n rl n (+r 2)lS 全 2 n r(l+r)n r(l+r) 22n (i+r 2)l+ n (+r 2) 4 nRVnr (即 nr)1 2 — nr 31—n h(ri+r 1r 2+r 22)34 0—nR 3表中I 、h 分别表示母线长、咼，r 表示圆柱、圆锥与球冠的底面 半径，r i 、「2分别表示 圆台上、下底面的半径，R 表示半径。

知识点一柱、锥、台、球的结构特征例1.下列叙述正确的是（）① 有两个面平行，其余各面都是平行四边形的几何体叫棱柱。

② 两个底面平行且相似，其余各面都是梯形的多面体是棱台。

223俯视图侧视图正视图第一章 空间几何体1.如图1,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )A.π7B. π8C. π10D. 12+π2.如图所示，正方体ABCD A B C D ''''-的棱长为1， ,E F 分别是棱AA '，CC '的中点，过直线,E F 的平面分别与棱BB '、DD '交于,M N ，设 BM x =，[0,1]x ∈，给出以下四个命题：（1）平面MENF ⊥平面BDD B ''； （2）当且仅当x =12时，四边形MENF 的面积最小； （3）四边形MENF 周长()L f x =，[0,1]x ∈是单调函数；（4）四棱锥C MENF '-的体积()V h x =为常函数； 以上命题中假命题．．．的序号为（ ）A ．（1）（4）B ．（2）C ．（3）D ．（3）（4）3.在空间直角坐标系Oxyz 中，已知()2,0,0A ，()2,2,0B ，()0,2,0C ，()1,1,2D ，若1S ，2S ，3S 分别表示三棱锥D A B C-在xO y ，yO z ，zOx 坐标平面上的正投影图形的面积，则（ ）A.123S S S ==B.12S S =且 31S S ≠C.13S S =且 32S S ≠D.23S S =且 13S S ≠4.已知如图所示的正方体ABCD ﹣A 1B 1C 1D 1，点P 、Q 分别在棱BB 1、DD 1上，且1111DD QD BB PB =过点A 、P 、Q 作截面截去该正方体的含点A 1的部分，则下列图形中不可能是截去后剩下几何体的主视图的是（ ）M NED'B'A'CDABB CD APM5.一个几何体的三视图如图所示，则该几何体的体积为（ ） A ．2 B ．1 C ．23D ．136.如图, 四棱锥P-ABCD 的底面ABCD 是边长为1的正方形, 面PAB ⊥面ABCD. 在面PAB 内的有一个动点M, 记M 到面PAD 的距离为d . 若1||22=-d MC , 则动点M 在面PAB 内的轨迹是( ) A.圆的一部分B.椭圆的一部分C.双曲线的一部分D.抛物线的一部分7.如图，在四面体ABCD 中，E ，F 分别为AB ，CD 的中点，过EF 任作一个平面α分别与直线BC ，AD 相交于点G ，H ，下列判断中:①对于任意的平面α，都有EFG EFH S S ∆∆=；②存在一个平面0α，使得点G 在线段BC 上，点H 在线段AD 的延长线上； ③对于任意的平面α，都有直线GF ，EH ，BD 相交于同一点或相互平行； ④对于任意的平面α，当G ，H 在线段BC ，AD 上时，几何体AC -EGFH 的体积是一个定值．其中正确的序号是 ( )A. ①③④B. ③④C. ②③D. ①②③8.如图，网格纸上小正方形的边长为1，实线画出的是某几何体的三视图，则此几何体的体积为（ ）A ．6B ．9C ．12D ．189.如图正方形OABC 的边长为1cm ，它是水平放置的一个平面图形的直观图，则原图形的周长是（ ）A ．cm 8B ．cm 6C ．cm )31(2+D ．cm )21(2+俯视图主视图xyCBAO10.如图，正方体 1111D C B A ABCD -的棱长为1，线段11D B 上有两个动点E ，F ，且1=2EF ，则下列结论中错误．．的是（ ） A ．BE AC ⊥ B ．ABCD EF 平面//C ．三棱锥BEF A -的体积为定值D ．AEF ∆的面积与BEF ∆的面积相等11.如图甲所示，三棱锥P ABC -的高8PO =，3AC BC ==，30ACB ∠=︒，M 、N 分别在BC 和PO 上，且CM x =，2((0,3])PN x x =∈，图乙中的四个图像大致描绘了三棱锥N AMC-的体积y 与x 的变化关系，其中正确的是（ ）12.若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为（ ）A ．8B ．338C ．38D ．34 13.一个棱锥的三视图如右图所示，则它的体积为 ( )A ．12 B ．32C ．1D ．1314.一条线段长为25，其侧视图长这5，俯视图长为34，则其正视图长为（ ）A ．5B ．34C ．6D ．4115.一个圆柱形的罐子半径是4米，高是9米，将其平放，并在其中注入深2米的水，截面如图所示，水的体积是（ ）平方米. A ．32424-π B ．33636-π C ．32436-π D ．33648-π主视图232 左视图俯视图B 1D 1C 1A 1AB CEFD16.下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）A ．①②B ．①③C ．①④D ．②④17.已知平面α∥平面β,直线l ⊂α,点P ∈l,平面α、β间的距离为8，则在β内到点P 的距离为10且到直线l 的距离为9的点的轨迹是（ ）A.一个圆B.两条直线C.四个点D.两个点18.正四棱锥ABCD V -的五个顶点在同一个球面上,若其底面边长为4,侧棱长为62,则此球的表面积为（ ）A π18B π36C π72D π9 19.如图是一个几何体的三视图（尺寸的长度单位为cm ），则它的体积是（ ）3cm .A. 33B. 18C. 2318+D. 320.已知某几何体的三视图如图，其中正视图中半圆的半径为1，则该几何体的体积为( )A ．24－32πB ．24－π3C ．24－πD ．24－π221.长方体一个顶点上的三条棱长分别是3、4、5，且它的8个顶点都在同一个球面上，则这个球的表面积是（ ）A ． π220B ．π225C ．π50D ． π200 22.如图, 在四面体ABCD 中, E, F 分别为AB, CD 的中点, 过EF 任作一个平面α分别与直线BC, AD 相交于点G, H, 有下列四个结论正确的个数是（ ） ①对于任意的平面α, 都有直线GF, EH, BD 相交于同一点; ②存在一个平面0α, 使得点G 在线段BC 上, 点H 在线段AD 的延长线上;③对于任意的平面α, 它把三棱锥的体积分成相等的两部分A. 0B. 1C. 2D. 3①正方体②圆锥③三棱台④正四棱俯视图1 1侧视图正视图32323.某三棱锥的三视图如图所示，该三棱锥的表面积是 ( )A ．28＋6 5B ．30＋6 5C ．56＋12 5D ．60＋12 524.如图，在四棱锥P －ABCD 中，侧面PAD 为正三角形，底面ABCD为正方形，侧面PAD ⊥底面ABCD ，M 为底面ABCD 内的一个动点，且满足MP ＝MC ，则点M 在正方形ABCD 内的轨迹为( )25.一个几何体的三视图如上图所示，则该几何体的体积为（ ）A.32πB.34πC. 43πD.23π26.设A 、B 、C 、D 是球面上的四点，AB 、AC 、A D 两两互相垂直，且3=AB ，4=AC ，11=AD ，则球的表面积为（ ） A.π36 B.π64 C. π100 D. π14427.如图，三棱锥V ABC -的底面为正三角形，侧面VAC 与底面垂直且VA VC =，已知其正视图的面积为23，侧视图的面积为( ) A ．32 B ．33C ．34D ．3628.已知P 是正四面体S ABC -的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（ ） A. 圆 B. 抛物线 C. 双曲线 D. 椭圆29.正方体1111ABCD A B C D -，棱长为4，点1A 到截面11AB D 的距离为( )A ． 163B ．433C ．34D ．3O PCBAS30.某四面体的三视图如图所示，三个三角形均为直角三角形，则该四面体的表面积是（ ） （A ）8（B ）34222+ （C ）2618+ （D ）2624+31.如图是一个空间几何体的三视图，则该几何体的外接球的表面积为（ ） A ．82π3B ．4πC ．8πD ．16π33. 以下几何体是由哪个平面图形旋转得到的（ ）A. B. C. D. 34.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ ）A ．34000cm 3B ．38000cm 3C ．32000cmD ．34000cm35.如图，正方体1111ABCD A B C D -，则下列四个命题： ①P 在直线1BC 上运动时，三棱锥1A D PC -的体积不变；②P 在直线1BC 上运动时，直线AP 与平面1ACD 所成角的大小不变； ③P 在直线1BC 上运动时，二面角1P AD C --的大小不变；④M 是平面1111A B C D 上到点D 和1C 距离相等的点，则M 点的轨迹是过1D 点的直线 其中真命题的个数是A ．1B ．2C ．3D ．436.已知正方体的棱长为1，且其顶点都在一个球面上，则该球的表面积为（ ） A ．π B ． 2π C ． 3π D ． 4π22222俯视图侧视图正视图223俯视图侧视图正视图37.某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（ ） A ．36cm 3B ．48cm 3C ．60cm 3D ．72cm 338.一个多面体的三视图如图所示，其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积和体积分别为( ) A ．88 ,48 B ．98 ,60 C ．108,72D ．158,12039.如图1,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )A.π7B. π8C. π10D. 12+π40.由平面六边形沿某一方向平移形成的空间几何体是( )A ．六棱锥B ．六棱台C ．六棱柱D ．非棱柱、棱锥、棱台的一个几何体41.下列说法中，正确的是( )A ．棱柱的侧面可以是三角形B ．若棱柱有两个侧面是矩形，则该棱柱的其它侧面也是矩形C ．正方体的所有棱长都相等D ．棱柱的所有棱长都相等42.将一个等腰梯形绕着它的较长的底边所在直线旋转一周，所得的几何体包括( )A ．一个圆台、两个圆锥B ．两个圆台、一个圆柱C ．两个圆台、一个圆锥D ．一个圆柱、两个圆锥43.将正三棱柱截去三个角(如图所示A ，B ，C 分别是△GHI 三边的中点)得到几何体如图2，则该几何体按图2所示方向的侧视图(或称左视图)为( )A B C D44.一个几何体的三视图如图所示，则该几何体的直观图可以是( )A．棱柱 B．棱台 C．圆柱 D．圆台45.如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为( )A．2 2 B. 2 C．2 3 D. 346.水以匀速注入某容器中，容器的三视图如图所示，其中与题中容器对应的水的高度h与时间t的函数关系图象是( )47.下列说法中正确的是( )A．棱柱的底面一定是平行四边形B．棱锥的底面一定是三角形C．棱锥被平面分成的两部分不可能都是棱锥D．棱柱被平面分成的两部分可以都是棱柱48.以下关于几何体的三视图的论述中，正确的是( )A．球的三视图总是三个全等的圆B．正方体的三视图总是三个全等的正方形C．水平放置的正四面体的三视图都是正三角形D．水平放置的圆台的俯视图是一个圆49.将正方体(如图a所示)截去两个三棱锥，得到图b所示的几何体，则该几何体的侧视图为( )50. 如图，某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为( )A ．6 3B ．93C ．12 3D ．18 351.圆柱的侧面展开图是边长为6π和4π的矩形，则圆柱的表面积为( )A ．6π(4π＋3)B ．8π(3π＋1)C ．6π(4π＋3)或8π(3π＋1)D ．6π(4π＋1)或8π(3π＋2)52.正三棱锥的底面边长为2，侧面均为直角三角形，则此三棱锥的体积为( )A.23 2B. 2C.23D.43 253.已知圆柱的底面直径与高都等于球的直径，则圆柱的体积与球体积之比为( )A ．1∶2B ．2∶1C ．2∶3D ．3∶254.如图，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，则该多面体的体积为( )A.23B.33C.43D.3255.某几何体的三视图如图所示，则它的体积是( )A ．8－2π3B ．8－π3C ．8－2πD ．2π356.已知某几何体的三视图如图所示，其中，正(主)视图、侧(左)视图均是由三角形与半圆构成，俯视图由圆与其内接三角形构成，根据图中的数据可得此几何体的体积为( )A.2π3＋12B.4π3＋16C.2π6＋16 D.2π3＋1257.已知圆锥的正视图是边长为2的等边三角形，则该圆锥体积为( )A .2π2B .2πC .3π3D .3π58.一个长方体共一顶点的三个面的面积分别是2，3，6，则这个长方体的体对角线的长是( ) A ．2 3 B ．3 2 C ．6 D . 659.一空间几何体的三视图如图所示，则该几何体的体积为( )A ．2π＋2 3B ．4π＋2 3C ．2π＋233D ．4π＋23360.某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是( )61.若某几何体的三视图如图所示，则这个几何体的直观图可以是( )62.将长、宽分别为4和3的长方形ABCD 沿对角线AC 折成直二面角，得到四面体A ­BCD ，则四面体A ­BCD 的外接球的表面积为( ) A ．25π B ．50π C ．5πD ．10π63.设M ，N 是球O 半径OP 上的两点，且NP ＝MN ＝OM ，分别过N ，M ，O 作垂直于OP 的平面，截球面得三个圆，则这三个圆的面积之比为( ) A ．3∶5∶6 B ．3∶6∶8 C ．5∶7∶9D ．5∶8∶964.已知三棱锥S ­ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( )A.26B.36C.23D.2265.如图，直三棱柱111C B A ABC -的侧棱长和底面边长均为2，其正（主）视图是边长为2的正方形，则此三棱柱侧（左）视图的面积为__________.66.若一个底面是正三角形的三棱柱的正视图如图所示，则其表面积等于________．67.如图是某个圆锥的三视图，根据图中所标尺寸可得俯视图中圆的面积为________，圆锥母线长为________．68. 用一张4cm×8cm 的矩形硬纸卷成圆柱的侧面，则圆柱轴截面的面积为________cm 2(接头忽略不计)．69.已知正三角形ABC 的边长为a ，那么△ABC 的平面直观图△A ′B ′C ′的面积为________． 70.已知圆锥的高与底面半径相等，则它的侧面积与底面积的比为________．71．棱长为1的正方体1111D C B A ABCD -的8个顶点都在球面O 的表面上，E 、F 分别是棱1AA 、1DD 的中点，则直线EF 被球O 截得的线段长为________．72.在棱长为1的正方体盒子里有一只苍蝇，苍蝇为了缓解它的无聊，决定要考察这个盒子的每一个角，它从一个角出发并回到原处，并且每个角恰好经过一次，为了从一个角到另一个角，它或直线飞行，或者直线爬行，苍蝇的路径最长是____________．（苍蝇的体积不计）73.如图, P 为60的二面角βα--l 内一点, P 到二面角两个面的距离分别为2、3, A 、B 是二面角的两个面内的动点,则△PAB 周长的最小值为 .74.已知一个球体的半径为1cm,若使其表面积增加到原来的2倍,表面积增加后球的体积为 75.在Rt △ABC 中，若∠C=90°，AC=b ，BC=a ，斜边AB 上的高为h ，则有结论h 2=，运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为a ，b ，c ，且三棱锥的直角顶点到底面的高为h ，则有结论： _________ ．123俯视图侧视图正视图76.若某空间几何体的三视图如图所示，则该几何体的体积是为77.一个几何体的三视图如图, 则这个几何体的体积为 .78.如图所示的三个直角三角形是 一个体积为20cm 3的几何体的三视图，则h ＝________cm.第76题图 第77题图 第78题图 79.正四面体ABC S 的所有棱长都为2，则它的体积为________．80.半径为5的球内包含有一个圆台, 圆台的上、下两个底面都是球的截面圆, 半径分别为3和4. 则该圆台体积的最大值为 .81.已知一个四棱锥的高为3，其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形，则此四棱锥的体积为________．82.长方体ABCD ­A 1B 1C 1D 1的8个顶点在同一个球面上，且AB ＝2，AD ＝3，AA 1＝1，则球面面积为________．83.若圆锥的侧面积为2π，底面面积为π，则该圆锥的体积为____________．84.已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是____________．85. 如图，半径为4的球O 中有一内接圆柱，当圆柱的侧面积最大时，球的表面积与该圆柱的侧面积之差是______．86.一个几何体的三视图如图所示，则该几何体的表面积为____________．87.已知某几何体的三视图如图所示，其中侧(左)视图是等腰直角三角形，正(主)视图是直角三角形，俯视图ABCD 是直角梯形，则此几何体的体积为_____________．88.如图，在三棱柱A 1B 1C 1­ABC 中，D ，E ，F 分别是AB ，AC ，AA 1的中点，设三棱锥F ­ADE 的体积为V 1，三棱柱A 1B 1C 1­ABC 的体积为V 2，则V 1∶V 2＝____________．89.半径为5的球内包含有一个圆台, 圆台的上、下两个底面都是球的截面圆, 半径分别为3和4. 则该圆台体积的最大值为 .90.一个几何体的三视图如图, 则这个几何体的体积为 .123俯视图侧视图正视图91.如图，在棱长为1的正方体1111ABCD A B C D -中，点, E F 分别是棱1,BC CC 的中点，P 是侧面11BCC B 内一点，若1//A P 平面,AEF 则线段1A P 长度的取值范围是___________.B 1C 1D 1A 1FE BC D A25411212111=+=+=MB B A M A 92.已知某几何体的俯视图是如图所示的矩形，正视图(或称主视图)是一个底边长为8，高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6，高为4的等腰三角形．(1)求该几何体的体积V ； (2)求该几何体的侧面积S .93.如图所示，球面上有四个点P，A，B，C，如果PA，PB，PC两两互相垂直，且PA＝PB＝PC＝a，求这个球的表面积．94.一个正三棱锥(底面是正三角形，顶点在底面的射影是底面正三角形的中心)的底面边长为6，侧棱长为15，求这个三棱锥的体积．95.如图，在△ABC中，∠ABC＝45°，∠BAC＝90°，AD是BC边上的高，沿AD把△ABD折起，使∠BDC＝90°.(1)证明：平面ADB⊥平面BDC；(2)若BD＝1，求三棱锥D­ABC的表面积．96. 圆锥底面半径为1cm，高为2cm，其中有一个内接正方体，求这个内接正方体的棱长.97. 用一个平行于圆锥底面的平面截这个圆锥，截得圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3cm，求圆台的母线长．98.某长方体的一条对角线长为7，在该长方体的正视图中，这条对角线的投影长为6，在该长方体的侧视图与俯视图中，这条对角线的投影长分别为a和b，求ab的最大值．99.已知一个几何体的三视图如图所示. （Ⅰ）求此几何体的表面积；（Ⅱ）在如图的正视图中，如果点A 为所在线段中点，点B 为顶点，求在几何体侧面上从点A 到点B 的最短路径的长.100.边长为2的正方形ABCD 中, BC F AB E ∈∈,(1) 如果E 、F 分别为AB 、B C 中点, 分别将△AED、△DCF、△BEF 沿ED 、DF 、FE 折起, 使A 、B 、C 重合于点P. 证明: 在折叠过程中, A 点始终在某个圆上, 并指出圆心和半径.(2) 如果F 为BC 的中点, E 是线段AB 上的动点, 沿DE 、DF 将△A ED 、△DCF 折起, 使A 、C 重合于点P, 求三棱锥P －DEF 体积的最大值.第二章 点、直线、平面之间位置关系1.如图，四棱锥S-ABCD 的底面为正方形，SD ⊥底面ABCD ， 则下列结论中不正确．．．的是（ A ．AC ⊥SBB ．AB ∥平面SCDC ．AB 与SC 所成的角等于DC 与SA 所成的角D ．SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角2.如图所示，正方体ABCD A B C D ''''-的棱长为1， ,E F 分别是棱AA '，CC '的中点，过直线,E F 的平面分别与棱BB '、DD '交于,M N ，设 BM x =，[0,1]x ∈，给出以下四个命题：（1）平面MENF ⊥平面BDD B ''；（2）当且仅当x =12时，四边形MENF 的面积最小；（3）四边形MENF 周长()L f x =，[0,1]x ∈是单调函数； （4）四棱锥C MENF '-的体积()V h x =为常函数； 以上命题中假命题．．．的序号为（ ） A ．（1）（4） B ．（2） C ．（3） D ．（3）（4）3.已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（ ）A ．,,m n m n αα若则‖‖‖B ．,,αγβγαβ⊥⊥若则‖C ．,,m m αβαβ若则‖‖‖D ．,,m n m n αα⊥⊥若则‖4.如图, 在四面体ABCD 中, E, F 分别为AB, CD 的中点, 过EF 任作一个平面α分别与直线BC, AD相交于点G, H, 有下列四个结论, 其中正确的个数是（ ）①对于任意的平面α, 都有直线GF, EH, BD 相交于同一点; ②存在一个平面0α, 使得点G 在线段BC 上, 点H 在线段AD 的延长线上; ③对于任意的平面α, 它把三棱锥的体积分成相等的两部分A. 0B. 1C. 2D. 35.如图，111C B A ABC -是直三棱柱，90=∠BCA ，点1D 和1F 分别是11B A 和11C A 的中点，若1CC CA BC ==，则1BD 与1AF 所成角的余弦值是（ ）A ．1030 B ．21C ．1530D ．1015M NED'B'A'CDAB6.在四棱锥ABCD P -中，底面ABCD 是菱形，⊥PA 底面ABCD ，M 是棱PC 上一点. 若a AC PA ==，则当MBD ∆的面积为最小值时，直线AC 与平面MBD 所成的角为（ ） A ．6π B.4π C.3π D.2π7.如果两直线b a //,且α平面//a ，则直线b 与平面α的位置关系是 ( ) A ．相交 B ．α//b C.α⊂b D. α//b 或α⊂b8.已知P 是正四面体S ABC -的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（ ） A . 圆 B . 抛物线 C . 双曲线 D . 椭圆 9.用c b a ,,表示三条不同的直线，γ表示平面， 给出下列命题，其中说法正确命题的序号是（ ） ①若c a c b b a //,//,//则； ②若c a c b b a ⊥⊥⊥则,,；③若b a b a //,//,//则γγ； ④若γγ⊥⊥b a ,则b a //. A ．①② B ．②③ C ．①④ D ．③④10.如图，正方体1111D C B A ABCD -的棱长为1，线段11D B 上有两个动点E ，F ，且1=2EF ，则下列结论中错误．．的是（ ） A ．BE AC ⊥ B ．ABCD EF 平面// C ．三棱锥BEF A -的体积为定值 D ．AEF ∆的面积与BEF ∆的面积相等11.在正方体1111ABCD A B C D -中，点P 在线段1AD 上运动，则异面直线CP 与1BA 所成的角θ的取值范围是( ) A ．03πθ<≤B ．02πθ<≤C ．03πθ≤≤D ．02πθ<≤12.已知m 、n 是两条不重合的直线，γβα,,是三个两两不重合的平面，给出下列四个命题：①若βαβα//,,则⊥⊥m m ； ②若βαβα//,//,,则n m n m ⊂⊂； ③若βαγβγα//,,则⊥⊥；④若m 、n 是异面直线，βααββα//,//,,//,则n n m m ⊂⊂ 其中真命题是（ ）A ．①和③B ．①和②C ．③和④D ．①和④O PBAS11C 1A 1ABCEFB CD APM13.下列命题中假命题．．．是( ) A ．垂直于同一条直线的两条直线相互垂直B ．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行C ．若一个平面经过另一个平面的垂线，那么这两个平面相互垂直D ．若一个平面内的两条相交直线与另一个平面内的相交直线分别平行，那么这两个平面相互平行14.如下图2, 在平行四边形A BCD 中, AD=2AB=2, ∠BA C =90°. 将△A CD 沿AC 折起, 使得BD=5. 在三棱锥D-ABC 的四个面中,下列关于垂直关系的叙述错误．．的是( ) A.面ABD⊥面BCD B.面ABD⊥面ACD C.面ABC ⊥面ACD D.面ABC ⊥面BCD15.在长方体1111D C B A ABCD -中，AB AD AA 21==．若F E ,分别为线段11D A ，1CC 的中点，则直线EF 与平面11A ADD 所成角的正弦值为 （ ） A ．36 B ．22 C ． 33 D ．3116.如图所示，在正方体1111D C B A ABCD -中，E ，F ，G ，H 分别为AA 1，AB ，BB 1，B 1C 1的中点。

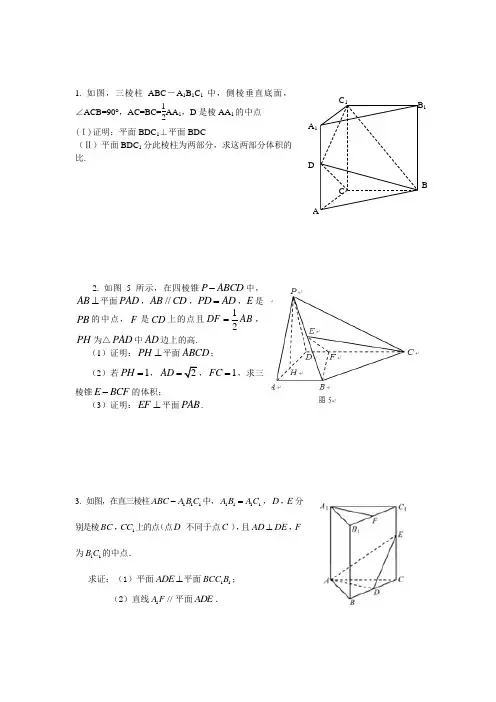
1. 如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比.2. 如图5所示，在四棱锥P ABCD -中，AB ⊥平面PAD ，//AB CD ，PD AD =，E 是PB 的中点，F 是CD 上的点且12DF AB =，PH 为△PAD 中AD 边上的高.（1）证明：PH ⊥平面ABCD ；（2）若1PH =，2AD =，1FC =，求三棱锥E BCF -的体积；（3）证明：EF ⊥平面PAB .3. 如图，在直三棱柱111ABC A B C -中，1111A B AC =，D E ，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F⊥，为11B C 的中点．求证：（1）平面ADE ⊥平面11BCC B ； （2）直线1//A F 平面ADE ．B 1C BADC 1A 14. 如图，四棱锥P —ABCD 中，ABCD 为矩形，△PAD 为等腰直角三角形，∠APD=90°，面PAD ⊥面ABCD ，且AB=1，AD=2，E 、F 分别为PC 和BD 的中点．（1）证明：EF ∥面PAD ； （2）证明：面PDC ⊥面PAD ； （3）求四棱锥P —ABCD 的体积．5. 在如图所示的几何体中，四边形ABCD 是正方形， MA ⊥平面ABCD ，//PD MA ，E 、G 、F 分别为MB 、PB 、PC 的中点，且2AD PD MA ==.（I ）求证：平面EFG ⊥平面PDC ；（II ）求三棱锥P MAB -与四棱锥P ABCD -的体积 之比.ABDPMFGE6. 如图，正方形ABCD 和四边形ACEF 所在的平面互相垂直。

EF//AC ，AB=2,CE=EF=1 （Ⅰ）求证：AF//平面BDE ； （Ⅱ）求证：CF ⊥平面BDF;7.如图，在多面体ABCDEF 中，四边形ABCD 是正方形，AB=2EF=2，EF ∥AB,EF ⊥FB,∠BFC=90°，BF=FC,H 为BC 的中点，(Ⅰ)求证：FH ∥平面EDB;（Ⅱ）求证：AC ⊥平面EDB; （Ⅲ）求四面体B —DEF 的体积；8. 如图，在直三棱柱111ABC A B C -中，E 、F 分别是1A B 、1A C 的中点，点D 在11B C 上，11A D B C⊥。