高中数学必修二第一章空间几何体的结构练习题

《空间几何体的结构》同步练习一、考点分析三视图是新课程改革中出现的内容，是新课程高考的热点之一，几乎每年都考，同学们要予以足够的重视．在高考中经常以选择、填空题的形式出现，属于基础或中档题，但也要关注三视图以提供信息为目的，出现在解答题中．这部分知识主要考查学生的空间想象能力与计算求解能力．二、典型例题知识点一：柱、锥、台、球的结构特征例1．下列叙述正确的是（）①有两个面平行，其余各面都是平行四边形的几何体叫棱柱．②两个底面平行且相似，其余各面都是梯形的多面体是棱台．③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台．④直角三角形绕其一条边旋转得到的旋转体是圆锥．⑤直角梯形以它的一条垂直于两底边的腰所在的直线为旋转轴，其余三边旋转形成的面围成的旋转体叫圆台．⑥用一个平面去截圆锥，底面和截面之间的部分是圆台．⑦通过圆锥侧面上一点，有无数条母线．⑧以半圆的直径所在直线为旋转轴，半圆面旋转一周形成球体．A．①②③④⑤⑥⑧B．①③④⑦⑧C．①②⑤⑧D．⑤思路分析：遇到概念判断问题，一定要在理解透彻相关概念的基础上，仔细分析，如果判断它是正确的，必须能紧扣定义，而不是模棱两可地去作判断；如果判断它是错误的，只需找到一个反例即可．解答过程：如图所示，由图（1）可知①是错误的；由图（2）可知②③是错误的；由图（3）可知④是错误的；由图（4）可知⑥是错误的．因为通过圆锥侧面上一点和圆锥的顶点只能连一条射线，所以“通过圆锥侧面上一点，有无数条母线．”是错误的，即⑦是不正确的．以半圆的直径所在直线为旋转轴，半圆旋转一周形成的应该是球面，半圆面旋转一周形成的才是球体．所以⑧是错误的．所以只有⑤是正确的．故应选D．解题后的思考：在作判断的时候没有严格的根据定义进行多角度分析，而是只抓住定义中的某一点就作出判断，容易导致错误．知识点二：组合体例2．如图，下列组合体是由哪几种简单几何体组成的？解答过程：（1）由一个三棱锥和一个四棱锥组成，为左右结构（2）由两个三棱锥组成，为上下结构（3）由圆锥和圆台组成，为上下结构知识点三：柱、锥的侧面展开图例3．小明在一个正方体盒子的每个面都写有一个字母，分别是：A、B、C、D、E、F，其平面展开图如图所示，那么在该正方体盒子中，和“A”相对的面所写的字母是哪一个？思路分析：在每个格子中标明你所想象的面的位置，如将A 格标明“上”，将B格标明“前”等等．解答过程：为字母“E”解题后的思考：本题突出考查了学生将正方体各面展开图复原为正方体的空间想象能力．例4．如图所示，为一个封闭的立方体，在它的六个面上标出A ，B ，C ，D ，E ，F 这六个字母，现放成下面三种不同的位置，所看见的表面上的字母已标明，则字母A ，B ，C 对面的字母分别是（ ）A ．D ，E ，FB ．F ，D ，EC ．E ，F ，D D ．E ，D ，F思路分析：本题处理方法比较灵活，要将几个图结合起来一起分析．解答过程：由（1）（2）两个图知，A 与B ，C ，D 相邻，结合第（3）个图知，B ，C 与F 共顶点，所以A 的对面为F ，同理B ，C 的对面分别为D ，E ，故选择B ．解题后的思考：本题考查推理能力以及空间想象能力．也可先结合图（1）（3）进行判断．例5．用长和宽分别是π3和π的矩形硬纸卷成圆柱的侧面，求圆柱的底面半径？思路分析：要注意哪条边是圆柱的母线，哪条边是圆柱底面的圆周．解答过程：设圆柱底面圆的半径为r ，由题意可知矩形长为底面圆的周长时，r ππ23=，解得23=r ．矩形宽为底面圆的周长时，r ππ2=，解得21=r ．故圆柱的底面半径为23或21．解题后的思考：本题学生经常会丢解，即主观认为只有图中所示的情况，即以π3作为底面周长，而忽视了它也可作为母线这种情况．知识点四 旋转体中的有关计算例6． 一个圆台的母线长cm 12，两底面面积分别为24cm π和225cm π，求：（1）圆台的高；（2）截得此圆台的圆锥的母线长．思路分析：通过作截得此圆台的圆锥的轴截面，构造直角三角形与相似三角形求解．解答过程：（1）作OA H A ⊥1242=∴=r r ππ 5252=∴=R R ππ3=∴AH153312221=-=∴H A（2）11O VA ∆ 与O VA ∆相似 AO O A VA VA 111=∴20=∴VA解题后的思考：通过构造旋转体的轴截面，将立体问题转化为平面问题．例7．已知球的两个平行截面的面积分别为π5和π8，且距离为3，求这个球的半径．思路分析：两截面的相互位置可能出现两种情况，一种是在球心O 的同侧，另一种是在球心O 的异侧．解答过程：（1）当两截面在球心O 的同侧时，如图所示，设这两个截面的半径分别为21,r r ，球心O 到截面的距离分别为21,d d ，球的半径为R ．8,5,8,522212221==∴=⋅=⋅r r r r ππππ ．又222221212d r d r R +=+= ，321222221=-=-∴r r d d ，即3))((2121=+-d d d d ．又321=-d d ，⎩⎨⎧=+=-∴,1,32121d d d d 解得⎩⎨⎧-==.1,221d d又∴>,02d 这种情况不成立．（2）当两截面在球心O 的异侧时，321=+d d ， 由上述解法可知3))((2121=+-d d d d ，⎩⎨⎧=-=+∴,1,32121d d d d 解得⎩⎨⎧==.1,221d d 3452121=+=+=∴d r R ．综上所述，这个球的半径为3．解题后的思考：同学们要注意不要只对同侧的情况进行讨论，而忽略对另一种位置关系的讨论．知识点五：画几何体的三视图例8．画出如图所示的三棱柱的三视图．思路分析：在正视图中，中间的竖线看不到，应画成虚线；侧视图是从左侧看三棱柱投射到竖直的正对着的平面上的正投影，所以不是三棱柱的一个侧面，而应该是过底面正三角形的一条高线的矩形．解答过程：解题后的思考：画三视图的时候要做到“长对正、宽相等、高平齐”，还要注意实线与虚线的区别．知识点六：三视图中的推测问题例9．根据下列三视图，说出各立体图形的形状．思路分析：三视图是从三个不同的方向看同一物体得到的三个视图．正视图反映物体的主要形状特征，主要体现物体的长和高，不反映物体的宽．而俯视图和正视图共同反映物体的长相等．侧视图和俯视图共同反映物体的宽相等．据此就不难得出该几何体的形状．解答过程：（1）圆台；（2）正四棱锥；（3）螺帽．解题后的思考：三视图的画法里要注意“长对正”，“高平齐”，“宽相等”，另外，还要熟悉基本空间几何体的三视图．知识点七：直观图的还原与计算问题例10．已知△A′B′C′是水平放置的边长为a 的正三角形ABC 的斜二测水平直观图，那么△A′B′C′的面积为_________．思路分析：先根据题意，画出直观图，然后根据△A′B′C′直观图的边长及夹角求解．解答过程：如图甲、乙所示的实际图与直观图．a OC C O a AB B A 4321,==''==''．在图乙中作C′D′⊥A′B′于D′，则a C O D C 8622=''=''．所以2166862121a a a D C B A S C B A =⨯⨯=''⋅''='''∆．故填2166a ． 解题后的思考：该题求直观图的面积，因此应在直观图中求解，需先求出直观图的底和高，然后用三角形面积公式求解．本题旨在考查同学们对直观图画法的掌握情况．例11．如图所示，正方形O′A′B′C′的边长为cm 1，它是水平放置的一个平面图形的直观图，则原图形的周长是____________．思路分析：先根据题意，由直观图画出原图形解答过程：逆用斜二测画法的规则画出原图如下图所示，由BC//OA 且BC=OA ，易知OABC 为平行四边形．在上图中，易求O′B′=2，所以OB =22．又OA =1，所以在Rt △BOA 中，31)22(22=+=AB ．故原图形的周长是)cm (8)13(2=+⨯，应填cm 8．解题后的思考：该题考查的是直观图与原图形之间的关系，及逆用斜二测画法的规则．。

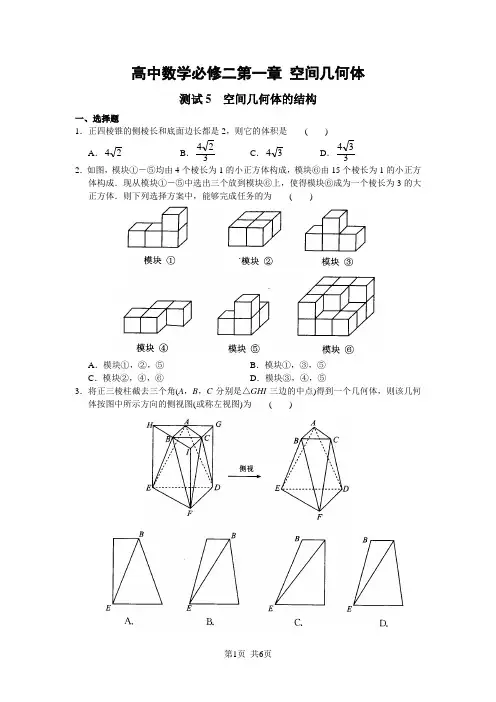
高中数学必修二第一章 空间几何体测试5 空间几何体的结构一、选择题1．正四棱锥的侧棱长和底面边长都是2，则它的体积是 ( ) A ．24B ．324 C ．34D ．334 2．如图，模块①－⑤均由4个棱长为1的小正方体构成，模块⑥由15个棱长为1的小正方体构成．现从模块①－⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为3的大正方体．则下列选择方案中，能够完成任务的为 ( )A ．模块①，②，⑤B ．模块①，③，⑤C ．模块②，④，⑥D ．模块③，④，⑤3．将正三棱柱截去三个角(A ，B ，C 分别是△GHI 三边的中点)得到一个几何体，则该几何体按图中所示方向的侧视图(或称左视图)为 ( )4．如果圆柱轴截面(经过上、下底面圆心的平面与圆柱相交所得的截面)的周长为6，那么圆柱体积的最大值是 ( ) A ．π3227 B ．8π C ．π827 D ．π二、填空题5．用一个平面去截体积为43π的球，所得截面的面积为π，则球心到截面的距离是________． 6．在正四棱柱ABCD －A 1B 1C 1D 1中，AB ＝a ，AA 1＝b ，P 为上底面中心，则四棱锥P －ABCD 的体积是________；当a ，b 满足条件________时，四棱锥P －ABCD 的侧面积比正四棱柱ABCD －A 1B 1C 1D 1的侧面积小．7．已知正方形ABCD 的边长是a ，E ，F 分别是AD ，CD 的中点，将正方形沿BE ，BF ，EF 折起，使得A ，D ，C 三点重合于一点，记该点为P ，则三棱锥P －BEF 的体积是________． 8．若两个长方体的长、宽、高分别为5cm ，4cm ，3cm ．把它们两个全等的面重合在一起构成一个大长方体，则大长方体的对角线最长为________． 三、解答题9．如图，在四棱锥S －ABCD 中，SD ⊥平面ABCD ，底面ABCD 是正方形，且SD ＝a ，AB ＝3a ．(1)求证：CD ⊥AS ；(2)求三棱锥D －SBC 的体积．10．如图，斜三棱柱ABC －A 1B 1C 1的底面是边长为4的正三角形，D 是BC 的中点，A 1D ⊥平面ABC ．(1)求证：BC ⊥A 1A ；(2)若A 1A ＝6，求三棱柱ABC －A 1B 1C 1的体积．11．如图，已知△ABC 中，∠BAC ＝90°，AB ＝m ，AC ＝n ．将△ABC 以BC 边为轴旋转一周，得到一个几何体．(1)求此几何体的体积；(2)设△ABC 的面积为21，求该几何体体积的最大值．12．如图，在三棱锥P －ABC 中，PC ⊥底面ABC ，AC ⊥BC ，D 是AB 的中点，且AC ＝BC＝1，)2π0(<<=∠θθPDC ． (1)求证：平面P AB ⊥平面PCD ； (2)记三棱锥P －ABC 的体积为V ，当⎥⎦⎤⎢⎣⎡∈126,122V 时，求θ的取值范围．参考答案测试5 空间几何体的结构一、选择题1．C 2．A 3．A 4．D 提示：4．设圆柱的底面半径为r ，高为h ，则4r ＋2h ＝6，即h ＝3－2r ． 圆柱的体积V ＝πr 2h ＝πr 2(3－2r )＝π(－2r 3＋3r 2)，则V '＝π(－6r 2＋6r )，令V '＝0，注意到r ＞0，解得r ＝1． 当r ∈(0，1)时，V ′＞0；当r ∈(1，＋∞)时，V ′＜0． 从而当r ＝1时，V 取得最大值π． 二、填空题 5．2 6．b a 231 b a 32< 7．3241a 8．cm 55 三、解答题9．(1)证明：∵SD ⊥平面ABCD ，∴CD ⊥SD ． 又四边形ABCD 是正方形，∴CD ⊥AD ． ∴CD ⊥平面SAD ，∴CD ⊥AS ． (2)解：三棱锥D －SBC 的体积3221)3(2131a a a V V BCD S SBC D =⨯⨯==--． 10．(1)证明：连接AD ．∵A 1D ⊥平面ABC ，∴BC ⊥A 1D ．∵D 是正三角形ABC 的边BC 的中点， ∴BC ⊥AD ，∴BC ⊥平面A 1AD ，∴BC ⊥A 1A ．(2)解：∵A 1D ⊥平面ABC ，∴A 1D ⊥AD ． 在Rt △A 1DA 中，AD ＝AB sin60°＝23， ∴622211=-=AD A A D A ．∴三棱柱ABC －A 1B 1C 1的体积224624432=⨯⨯=V ． 11．(1)解：作AD ⊥BC 于D ．依题意，所得几何体为两个共底面的圆锥． 在Rt △ABC 中，∵2222n m AC AB BC +=+=，∴22nm mnBC AC AB AD +=⋅=．∴该几何体的体积为 2222223ππ31)(π31n m n m BC AD DC BD AD V +=⋅=+⋅=． (2)解：∵△ABC 的面积为21，∴mn ＝1． ∵m 2＋n 2≥2mn ＝2，∴,π62213π3π2222=≤+=n m n m V∴当且仅当m ＝n ＝1时，该几何体的体积取得最大值π62． 12．(1)∵AC ＝BC ，∴△ACB 是等腰三角形， 又D 是AB 的中点，∴CD ⊥AB ，又PC ⊥底面ABC ，∴PC ⊥AB ， ∴AB ⊥平面PCD ． 又AB ⊂平面P AB ，∴平面P AB ⊥平面PCD ． (2)在Rt △PCD 中，,22=CD θθtan 22tan =⋅=CD PC ∴三棱锥P －ABC 的体积PC S V ABC ⋅=∆31,tan 122tan 222131θθ=⨯⨯=令,126tan 122122≤≤θ得,3tan 1≤≤θ ∵2π0<<θ，∴3π4π≤≤θ．。

第一章章节测试题YC一、选择题：1．不共面的四点能够确立平面的个数为（）A ． 2 个B． 3 个C． 4 个 D ．没法确立2．利用斜二测画法获得的①三角形的直观图必定是三角形；②正方形的直观图必定是菱形；③等腰梯形的直观图能够是平行四边形；④菱形的直观图必定是菱形 .以上结论正确的选项是（）A ．①②B．①C．③④ D ．①②③④3．棱台上下底面面积分别为16 和 81,有一平行于底面的截面面积为36,则截面戴的两棱台高的比为（）A ．1∶ 1B． 1∶ 1C． 2∶ 3 D ． 3∶44．若一个平行六面体的四个侧面都是正方形,则这个平行六面体是（）A ．正方体B．正四棱锥C．长方体 D ．直平行六面体5．已知直线 a、 b 与平面α、β、γ，以下条件中能推出α∥β的是（）A ．a⊥α且 a⊥βB．α⊥γ且β⊥γC．a α， b β， a∥ b D． a α， bα， a∥β， b∥β6．如下图，用符号语言可表达为（）A ．α∩β＝ m， nα， m∩ n＝AB ．α∩β＝ m，n∈α， m∩ n＝ AC．α∩β＝ m，nα， A m， A nD ．α∩β＝ m， n∈α， A ∈ m， A ∈ n7．以下四个说法① a//α， b α ,则 a// b②a∩α＝ P， bα，则 a 与 b 不平行③ a α，则 a//α④a// α， b //α，则 a// b此中错误的说法的个数是（）A ．1 个B． 2 个C． 3 个 D ． 4 个8．正六棱台的两底边长分别为1cm,2cm, 高是 1cm,它的侧面积为（）97B．9 7 cm223 cm2 D ． 3 2 cm2A ．cm2C．239．将一圆形纸片沿半径剪开为两个扇形，其圆心角之比为3∶ 4.再将它们卷成两个圆锥侧面，则两圆锥体积之比为（）A ．3∶ 4B． 9∶ 16C． 27∶64 D ．都不对10．将边长为 a 的正方形ABCD 沿对角线AC 折起，使BD =a，则三棱锥D— ABC 的体积为（）a3a33a32a3A ．B．C． D ．6121212二、填空题：11．螺母是由 _________和两个简单几何体组成的．12．一个长方体的长、宽、高之比为2：1： 3，全面积为 88cm2，则它的体积为 ___________ ．13．如图，将边长为 a 的正方形剪去暗影部分后，围成一个正三棱锥，则正三棱锥的体积是．14．空间四边形、 、 G 、H 分别是ABCD 中， E F、 BC 、CD 、DA 的中点 .①若 AC=BD ，AB则四边形 EFGH 是；②若 ACBD ， 则四边形 EFGH 是．三、解答题： 解答应写出文字说明、证明过程或演算步骤 (共 76 分 )．15．（ 12 分）将以下几何体按构造分类填空①集装箱；②油罐；③排球；④羽毛球；⑤橄榄球；⑥氢原子；⑦魔方；⑧金字塔；⑨三棱镜；⑩滤纸卷成的漏斗；○11量筒；○ 量杯；○ 十字架．1213（ 1）拥有棱柱构造特点的有 ；（ 2）拥有棱锥构造特点的有 ；（ 3）拥有圆柱构造特点的有 ；（ 4）拥有圆锥构造特点的有 ；（ 5）拥有棱台构造特点的有 ；（ 6）拥有圆台构造特点的有 ；（ 7）拥有球构造特点的有；（ 8）是简单会合体的有；（ 9）其余的有．16．（ 12 分）已知： a,b ,a b A, P b, PQ // a.求证： PQ .．17．（ 12 分）正四棱台的侧棱长为 3cm ，两底面边长分别为 1cm 和 5cm ，求体积．18．（ 12 分）直平行六面体的底面是菱形，两个对角面面积分别为 Q 1， Q 2 ，求直平行六面体的侧面积．19．（14 分）已知四棱台上，下底面对应边分别是a，b，试求此中截面把此棱台侧面分红的两部分面积之比．20．（ 14 分）如图，直三棱柱 ABC— A1B1C1中， AC ＝ BC ＝1，∠ ACB ＝ 90°， AA1＝ 2 ，D是 A1B1中点．（1）求证 C1 D ⊥平面 A1B ；（ 2）当点 F 在 BB1上什么地点时，会使得 AB1⊥平面C1DF ？并证明你的结论．参照答案（五）一、 CBCDA ACADD ．二、 11．正六棱柱，圆柱； 12．48cm 31313) 13a2； 14．菱形，矩形 .；．(212三、 15．⑴①⑦⑨；⑵⑧；⑶⑾；⑷⑩；⑸⒁；⑹⑿⒃；⑺③⑥⒂；⑻②④⒀；⑼⑤. 16．此题主要考察用平面公义和推论证明共面问题的方法.证明∵ PQ∥ a,∴PQ 与 a 确立一个平面,直线 a,点P.p b,b,p又 a与重合PQ17．解：正四棱台ABCD A1 B1C1 D1O1 , O是两底面的中心A1 C1 2 ，AC 5 2A1O12AO 5 2 222O1O 3 252212211 1 [125212 52]1[1 25 5]31( cm 3 )Vh[ S SSS ]333318．解：设底面边长为 a ， 侧棱长为 l ， 两对角线分别为c ， d.c lQ 1 (1)则d l Q 2 (2)1 21 2c22da (3)2消去 c ， d 由（ 1）得 cQ 1，由（ 2）得 dQ 2， 代入（ 3）得ll221 Q 1 1 Q 2a 2Q 1 2 Q 2 2 4l 2a 22laQ 12Q 2 22 l 2 lS 侧 4al2 Q 1 2 Q 2219．解：设 A 1B 1C 1D 1 是棱台 ABCD －A 2B 2C 2D 2 的中截面，延伸各侧棱交于P 点.2 21 1a b∵ BC ∥B 11 S ∵ BC=a ，B C =b ∴ B C =C ∴2S(a b)2∴ S PB 1 C 14a2S PBCPBCa 2 PB 1C 1a b 2 ()2同理SPB 2 C 2b 2SPBCSB 1C 1CBSPB 1C 1SPBCa2∴S B C C BSPB C2SPB C2 2 1 121 1(a b) 24a2122ab2(b3a)(b a) b 3ab3ab 2 (ab) 23b 2 2ab a 2(3b a)(b a)3b aa 24a 2同理：SABB 1 A 1S DCC 1 D 1SADD 1 A 1b 3a SA 1B 1 B 2 A 1SD 1 C 1C 2 D 2SA 1D 1D 2 A 13b a由等比定理，得S 上棱台侧＝ 3a bS 下棱台侧a 3b20．（ 1）证明：如图 ，∵ABC — A 1B 1C 1 是直三棱柱，∴ A 1C 1 ＝ B 1C 1 ＝ 1，且∠ A 1C 1B 1 ＝90°．又D 是B 的中点 ，∴CD ⊥ A B 1．A 1 111∵ AA 1 ⊥ 平面 A 1B 1C 1 ， C 1D 平面 A 1B 1C 1 ，∴ AA 1 ⊥ C 1D ，∴ C 1D ⊥ 平面 AA 1B 1B ．（2）解：作DE ⊥ AB 1 交 AB 1 于 E ， 延伸 DE 交 BB 1 于 F ， 连接 C 1F ， 则 AB 1 ⊥ 平面 C 1DF ， 点 F 即为所求．事实上，∵C1D ⊥平面 AA1BB ， AB1平面 AA1B1B ，∴C1D ⊥AB1．又 AB1⊥DF ， DF C1D ＝ D ，∴AB 1⊥ 平面C1DF ．。

人教版高中数学必修2第一章-空间几何体练习题及答案(全)第一章空间几何体1.1 空间几何体的结构一、选择题1、下列各组几何体中是多面体的一组是（）A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、下列说法正确的是（）A 有一个面是多边形，其余各面是三角形的多面体是棱锥B 有两个面互相平行，其余各面均为梯形的多面体是棱台C 有两个面互相平行，其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行，侧面均为平行四边形3、下面多面体是五面体的是（）A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、下列说法错误的是（）A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是（）A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中，直角三角形最多可有几个（）A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面，面数最少的棱柱有————————个顶点，有—————————个棱。

8、一个棱柱有10个顶点，所有侧棱长的和为60，则每条侧棱长为————————————9、把等腰三角形绕底边上的高旋转1800，所得的几何体是——————10、水平放置的正方体分别用“前面、后面、上面、下面、左面、右面”表示。

图中是一个正方体的平面展开图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面。

则“祝”“你”“前”分别表示正方体的—————祝你前程似锦一、选择题1、两条相交直线的平行投影是（）A 两条相交直线B 一条直线C 一条折线D 两条相交直线或一条直线2、如图中甲、乙、丙所示，下面是三个几何体的三视图，相应的标号是（）①长方体②圆锥③三棱锥④圆柱A ②①③B ①②③C ③②④D ④③②。

数学《必修2》第一章“空间几何体”测试题一、选择题：(本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符号题目要求的)１．利用斜二测画法得到的：①三角形的直观图一定是三角形；②正方形的直观图一定是正方形；③等腰梯形的直观图一定是等腰梯形；④平行四边形的直观图一定是平行四边形。

以上结论正确的是（）Ａ.①②Ｂ.①④Ｃ.③④Ｄ. ①②③④2．下列说法正确的是（）A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有的几何体的表面都能展开成平面图形D.棱柱的各条棱都相等3．圆台的母线长为6，两底面半径分别为2、7，则圆台的侧面积为（）A.54πB.8πC.4πD.164．给出下列结论：①圆柱的母线是其上底面圆周上任意一点与下底面圆周上任意一点的连线；②圆锥的母线是圆锥顶点与底面圆周上任意一点的连线；③圆台的母线是圆台上、下底面圆周上任意两点的连线。

其中正确的是（）A.①②B.②③C.①③D.②。

5．已知底面为正方形的长方体的各顶点都在一个球面上，长方体的高为4，体积为16，则这个球的表面积是（）A.16πB.20πC.24πD.32π6．下列说法错误的是（）A.棱柱最少有5个面B.棱锥最少有4个面C.棱台的底面有2个D.棱锥的底面边数和侧棱数不一定相同7．下列四个图形不是下图1中几何体的三视图之一的是（）图1 A B C D8．下面几何体中，过轴的截面一定是圆面的是（ ）A.圆柱B.圆锥C.球D.圆台 9．正方体的表面积是96，则正方体的体积是（ ）A. B.64 C.16 D. 96 10．若某几何体的三视图如图所示，则这个几何体的直观图可以是（ ）二、填空题：(本大题共5个小题，每小题5分，共25分)11．半径为2的球的体积等于 ，表面积等于12．圆锥的侧面展开图为圆心角为120、半径为1的扇形，则圆锥的侧面积为 13．如下图所示，等腰梯形ABCD ，上底1CD =，腰AD CB ==3AB =，以下底所在直线为x 轴，则由斜二测画法画的直观图''''A B C D 的面积为 14．某几何体的三视图如下图所示, 则其体积为_______.15．某几何体的三视图如下图所示,则该几何体的体积是____________.第13题图14题图第15题图三、解答题：(本大题共6个小题，共75分，解答应写出文字说明，证明过程或演算步骤)16．求下列几何体的体积与表面积。

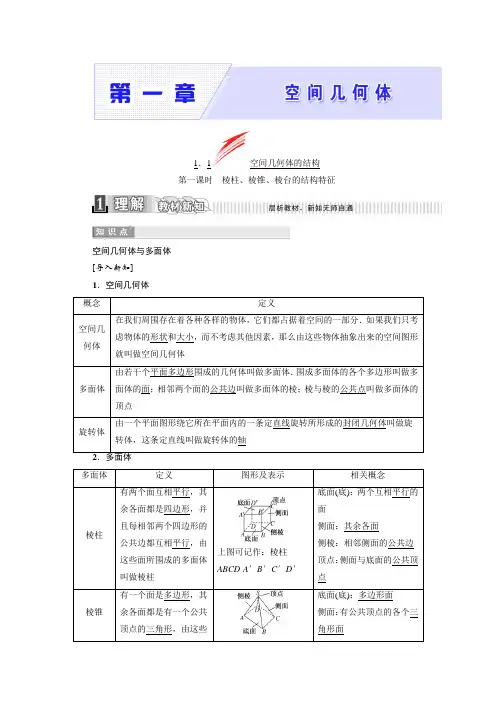
1．1空间几何体的结构第一课时棱柱、棱锥、棱台的结构特征空间几何体与多面体[导入新知]1．空间几何体1．对于多面体概念的理解，注意以下两个方面：(1)多面体是由平面多边形围成的，围成一个多面体至少要4个面．一个多面体由几个面围成，就称为几面体．(2)多面体是一个“封闭”的几何体，包括其内部的部分． 2．棱柱具有以下结构特征和特点：(1)侧棱互相平行且相等，侧面都是平行四边形．(2)两个底面与平行于底面的截面是全等的多边形，如图a 所示．(3)过不相邻的两条侧棱的截面是平行四边形，如图b 所示．(4)有两个面平行，其余各面都是平行四边形的几何体不一定是棱柱，如图c 所示．3．对于棱锥要注意有一个面是多边形，其余各面都是三角形的几何体不一定是棱锥，必须强调其余各面是共顶点的三角形，如图d 所示．4．棱台中各侧棱延长后必相交于一点，否则不是棱台．棱柱的结构特征[例1]下列关于棱柱的说法：(1)所有的面都是平行四边形；(2)每一个面都不会是三角形；(3)两底面平行，并且各侧棱也平行；(4)被平面截成的两部分可以都是棱柱．其中正确说法的序号是________．[答案](3)(4)[类题通法]有关棱柱的结构特征问题的解题策略(1)紧扣棱柱的结构特征进行有关概念辨析．①两个面互相平行；②其余各面是四边形；③相邻两个四边形的公共边互相平行．求解时，首先看是否有两个平行的面作为底面，再看是否满足其他特征．(2)多注意观察一些实物模型和图片便于反例排除．[活学活用]下列说法正确的是()A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．各个侧面都是正方形的四棱柱一定是正方体D．九棱柱有9条侧棱，9个侧面，侧面均为平行四边形答案：D棱锥、棱台的结构特征[例2]下列关于棱锥、棱台的说法：(1)用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；(2)棱台的侧面一定不会是平行四边形；(3)棱锥的侧面只能是三角形；(4)由4个面围成的封闭图形只能是三棱锥；(5)棱锥被平面截成的两部分不可能都是棱锥．其中说法正确的序号是________．[答案](2)(3)(4)[类题通法]判断棱锥、棱台形状的两个方法(1)举反例法：结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．(2)直接法：下列说法正确的有()①由5个面围成的多面体只能是四棱锥；②仅有两个面互相平行的五面体是棱台；③两个底面平行且相似，其余各面都是梯形的多面体是棱台；④有两个面互相平行，其余4个面都是等腰梯形的六面体是棱台．A．0个B．1个C．2个D．3个答案：A多面体的平面展开图[例3]如下图是三个几何体的侧面展开图，请问各是什么几何体？[解]由几何体的侧面展开图的特点，结合棱柱，棱锥，棱台的定义，可把侧面展开图还原为原几何体，如图所示：所以①为五棱柱，②为五棱锥，③为三棱台．[类题通法]1．解答此类问题要结合多面体的结构特征发挥空间想象能力和动手能力．2．若给出多面体画其展开图时，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面．3．若是给出表面展开图，则可把上述程序逆推．[活学活用]水平放置的正方体的6个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图(图中数字写在正方体的外表面上)，若图中“0”上方的“2”在正方体的上面，则这个正方体的下面是()A．1B．5C．快D．乐答案：B1.柱、锥、台结构特征判断中的误区[典例]如下图所示，下列关于这个几何体的正确说法的序号为________．①这是一个六面体；②这是一个四棱台；③这是一个四棱柱；④此几何体可由三棱柱截去一个三棱柱得到；⑤此几何体可由四棱柱截去一个三棱柱得到．[解析]①正确，因为有6个面，属于六面体的范围；②错误，因为侧棱的延长线不能交于一点，所以不正确；③正确，如果把几何体放倒就会发现是一个四棱柱；④⑤都正确，如下图所示．[答案]①③④⑤[易错防范]1．解答过程中易忽视侧棱的延长线不能交于一点，直观感觉是棱台，而不注意逻辑推理．2．解答空间几何体概念的判断题时，要注意紧扣定义，切忌只凭图形主观臆断．[成功破障]如右图所示，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是()A．棱柱B．棱台C．棱柱与棱锥的组合体D．不能确定答案：A一、选择题1．下列图形中，不是三棱柱的展开图的是()答案：C2.如右图所示，在三棱台ABC-A′B′C′中，截去三棱锥A′-ABC，则剩余部分是()A．三棱锥B．四棱锥C．三棱柱D．组合体答案：B3．下列说法正确的是()①棱锥的各个侧面都是三角形；②三棱柱的侧面为三角形；③四面体的任何一个面都可以作为棱锥的底面；④棱锥的各侧棱长都相等．A．①②B．①③C．②③D．②④答案：B4．正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有()A．20 B．15C．12 D．10答案：D5．下列命题正确的是()A．用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台B．棱柱中两个互相平行的面一定是棱柱的底面C．棱台的底面是两个相似的正方形D．棱台的侧棱延长后必交于一点答案：D二、填空题6．面数最少的棱柱为________棱柱，共有________个面围成．答案：三 57.如右图所示，M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点，沿正方体表面从点A到点M的最短路程是________ cm.答案：138．侧棱垂直于底面的棱柱叫做直棱柱．侧棱不垂直于底面的棱柱叫做斜棱柱．底面是正多边形的直棱柱叫做正棱柱．底面是平行四边形的四棱柱叫做平行六面体．侧棱与底面垂直的平行六面体叫做直平行六面体．底面是矩形的直平行六面体叫做长方体．棱长都相等的长方体叫做正方体．请根据上述定义，回答下面的问题：(1)直四棱柱________是长方体；(2)正四棱柱________是正方体．(填“一定”“不一定”或“一定不”)答案：(1)不一定(2)不一定三、解答题9．如右图所示，长方体ABCD -A1B1C1D1.(1)这个长方体是棱柱吗？如果是，是几棱柱？为什么？(2)用平面BCNM把这个长方体分成两部分，各部分形成的几何体还是棱柱吗？如果是，是几棱柱，并用符号表示；如果不是，请说明理由．解：(1)是棱柱，并且是四棱柱，因为长方体相对的两个面是互相平行的四边形(作底面)，其余各面都是矩形(作侧面)，且相邻侧面的公共边互相平行，符合棱柱的定义．(2)截面BCNM的上方部分是三棱柱BB1M-CC1N，下方部分是四棱柱ABMA1-DCND1.10．给出两块正三角形纸片(如图所示)，要求将其中一块剪拼成一个底面为正三角形的三棱锥模型，另一块剪拼成一个底面是正三角形的三棱柱模型，请设计一种剪拼方案，分别用虚线标示在图中，并作简要说明．解：如图①所示，沿正三角形三边中点连线折起，可拼得一个底面为正三角形的三棱锥．如图②所示，正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的14，有一组对角为直角，余下部分按虚线折成，可成为一个缺上底的底面为正三角形的三棱柱，而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底.第二课时 圆柱、圆锥、圆台、球的结构特征 简单组合体的结构特征旋转体 [导入新知]1．以直角三角形斜边所在的直线为旋转轴，其余两边旋转成的曲面围成的旋转体不是圆锥．2．球与球面是完全不同的两个概念，球是指球面所围成的空间，而球面只指球的表面部分．3．圆台也可以看作是等腰梯形以其底边的垂直平分线为轴，各边旋转半周形成的曲面所围成的几何体．简单组合体[导入新知]1．简单组合体的概念由简单几何体组合而成的几何体叫做简单组合体．2．简单组合体的构成形式有两种基本形式：一种是由简单几何体拼接而成的；另一种是由简单几何体截去或挖去一部分而成的．[化解疑难]简单组合体识别的要求(1)准确理解简单几何体(柱、锥、台、球)的结构特征．(2)正确掌握简单组合体构成的两种基本形式．(3)若用分割的方法，则需要根据几何体的结构特征恰当地作出辅助线(或面)．旋转体的结构特征[例1]给出下列说法：(1)以直角三角形的一条边所在直线为轴，其余两边旋转形成的曲面围成的几何体是圆锥；(2)以等腰三角形底边上的中线所在直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥；(3)经过圆锥任意两条母线的截面是等腰三角形；(4)圆锥侧面的母线长有可能大于圆锥底面圆直径．其中说法正确的序号是________．[答案](2)(3)(4)[类题通法]1．判断简单旋转体结构特征的方法(1)明确由哪种平面图形旋转而成．(2)明确旋转轴是哪条直线．2．简单旋转体的轴截面及其应用(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量．(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想．[活学活用]给出下列说法：(1)圆柱的底面是圆面；(2)经过圆柱任意两条母线的截面是一个矩形面；(3)圆台的任意两条母线的延长线可能相交，也可能不相交；(4)夹在圆柱的两个截面间的几何体还是一个旋转体．其中说法正确的是________．答案：(1)(2)简单组合体[例2]观察下列几何体的结构特点，完成以下问题：(1)题图①所示几何体是由哪些简单几何体构成的？试画出几何图形，可旋转该图形180°后得到几何体①.(2)题图②所示几何体的结构特点是什么？试画出几何图形，可旋转该图形360°得到几何体②.(3)题图③所示几何体是由哪些简单几何体构成的？请说明该几何体的面数、棱数、顶点数．[解](1)图①是由圆锥和圆台组合而成．可旋转如下图形180°得到几何体①.(2)图②是由一个圆台，从上而下挖去一个圆锥，且圆锥的顶点恰为圆台底面圆的圆心．可旋转如下图形360°得到几何体②.(3)图③是由一个四棱锥与一个四棱柱组合而成，且四棱锥的底面与四棱柱底面相同．共有9个面，9个顶点，16条棱．[类题通法]1．明确组合体的结构特征，主要弄清它是由哪些简单几何体组成的，必要时也可以指出棱数、面数和顶点数，如题图③所示的组合体有9个面，9个顶点，16条棱．2．会识别较复杂的图形是学好立体几何的第一步，因此我们应注意观察周围的物体，然后将它们“分拆”成几个简单的几何体，进而培养我们的空间想象能力和识图能力．[活学活用]指出图①～图③的3个几何体分别是由哪些简单几何体组成的．解：图①几何体由一个圆锥、一个圆柱和一个圆台拼接而成；图②几何体由一个六棱柱和一个圆柱拼接而成；图③几何体由一个六棱柱挖去一个圆柱而成．1.旋转体的生成过程[典例]如右图所示，四边形ABCD为直角梯形，试作出绕其各条边所在的直线旋转所得到的几何体．[解题流程][规范解答]以边AD所在直线为旋转轴旋转，形成的几何体是圆台，如图①所示．以边AB所在直线为旋转轴旋转，形成的几何体是一个圆锥和一个圆柱拼接而成的几何体，如图②所示．以边CD所在直线为旋转轴旋转，形成的几何体是一个圆柱挖掉一个圆锥构成的几何体，如图③所示．以边BC所在直线为旋转轴旋转，形成的几何体是由一个圆台挖掉一个圆锥构成的几何体和一个圆锥拼接而成，如图④所示．[活学活用]一个有30°角的直角三角板绕其各条边所在直线旋转一周所得几何体是圆锥吗？如果以斜边上的高所在的直线为轴旋转180°得到什么几何体？旋转360°又得到什么几何体？解：如图①和图②所示，绕其直角边所在直线旋转一周围成的几何体是圆锥．如图③所示，绕其斜边所在直线旋转一周所得几何体是两个同底相对的圆锥．如图④所示，绕其斜边上的高所在的直线为轴旋转180°围成的几何体是两个半圆锥，旋转360°围成的几何体是一个圆锥．一、选择题1．下列说法正确的是()A．平行于圆锥某一母线的截面是等腰三角形B．平行于圆台某一母线的截面是等腰梯形C．过圆锥顶点的截面是等腰三角形D．过圆台上底面中心的截面是等腰梯形答案：C2．将一个等腰梯形绕它的较长的底边所在的直线旋转一周，所得的几何体包括() A．一个圆台、两个圆锥B．两个圆台、一个圆柱C．两个圆柱、一个圆台D．一个圆柱、两个圆锥答案：D3．以钝角三角形的较小边所在的直线为轴，其他两边旋转一周所得到的几何体是() A．两个圆锥拼接而成的组合体B．一个圆台C．一个圆锥D．一个圆锥挖去一个同底的小圆锥答案：D4．下列叙述中正确的个数是()①以直角三角形的一边所在直线为轴旋转所得的旋转体是圆锥；②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台；③圆柱、圆锥、圆台的底面都是圆面；④用一个平面去截圆锥，得到一个圆锥和一个圆台．A．0 B．1C．2 D．3答案：B5.如右图所示的几何体，关于其结构特征，下列说法不正确的是()A．该几何体是由两个同底的四棱锥组成的几何体B．该几何体有12条棱、6个顶点C．该几何体有8个面，并且各面均为三角形D．该几何体有9个面，其中一个面是四边形，其余均为三角形答案：D二、填空题6．有下列说法：①在圆柱的上、下底面的圆周上各取一点，则这两点连线是圆柱的母线；②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在直线是互相平行的．其中正确的是________(把所有正确说法的序号都填上)．答案：②④7．下面这个几何体的结构特征是_____________________________________.答案：由一个四棱锥、一个四棱柱拼接，又在四棱柱中挖去了一个圆柱而成8．如图是一个几何体的表面展成的平面图形，则这个几何体是________．答案：圆柱三、解答题9．指出如图①、图②、图③所示的图形分别是由哪些简单几何体构成的．解：分割原图，使它的每一部分都是简单几何体．图①是由一个三棱柱和一个四棱柱拼接而成的简单组合体；图②是由一个圆锥和一个四棱柱拼接而成的简单组合体；图③是由一个半球、一个圆柱和一个圆台拼接而成的简单组合体．10.如右图所示，用一个平行于圆锥SO底面的平面截这个圆锥，截得圆台上、下底面的半径分别为2 cm和5 cm，圆台的母线长是12 cm，求圆锥SO的母线长．解：如右图所示，过圆台的轴作截面，截面为等腰梯形ABCD ，由已知可得上底半径O 1A ＝2 cm ，下底半径OB ＝5 cm ，且腰长AB ＝12 cm.设截得此圆台的圆锥的母线长为l ，则由△SAO 1∽△SBO ，可得l －12l ＝25，所以l ＝20 cm ，即截得此圆台的圆锥的母线长为20 cm.1．2空间几何体的三视图和直观图1.2.1 & 1.2.2 中心投影与平行投影 空间几何体的三视图中心投影与平行投影 [导入新知] 1．投影的定义由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做投影．其中，把光线叫做投影线，把留下物体影子的屏幕叫做投影面．2．中心投影与平行投影平行投影和中心投影都是空间图形的一种画法，但二者又有区别 (1)中心投影的投影线交于一点，平行投影的投影线互相平行．(2)平行投影下，与投影面平行的平面图形留下的影子，与这个平面图形的形状和大小完全相同；而中心投影则不同．三 视 图 [导入新知]1．每个视图都反映物体两个方向上的尺寸．正视图反映物体的上下和左右尺寸，俯视图反映物体的前后和左右尺寸，侧视图反映物体的前后和上下尺寸．2．画几何体的三视图时，能看见的轮廓线和棱用实线表示，看不见的轮廓线和棱用虚线表示．中心投影与平行投影 [例1] 下列说法中：①平行投影的投影线互相平行，中心投影的投影线相交于一点；②空间图形经过中心投影后，直线变成直线，但平行线可能变成了相交的直线； ③两条相交直线的平行投影是两条相交直线． 其中正确的个数为( ) A ．0 B ．1 C ．2 D ．3[答案] B [类题通法]1．判定几何体投影形状的方法．(1)判断一个几何体的投影是什么图形，先分清楚是平行投影还是中心投影，投影面的位置如何，再根据平行投影或中心投影的性质来判断．(2)对于平行投影，当图形中的直线或线段不平行于投影线时，平行投影具有以下性质： ①直线或线段的投影仍是直线或线段； ②平行直线的投影平行或重合；③平行于投影面的线段，它的投影与这条线段平行且等长；④与投影面平行的平面图形，它的投影与这个图形全等；⑤在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比．2．画出一个图形在一个平面上的投影的关键是确定该图形的关键点，如顶点、端点等，方法是先画出这些关键点的投影，再依次连接各投影点即可得此图形在该平面上的投影．[活学活用]如右图所示，在正方体ABCD -A′B′C′D′中，E，F分别是A′A，C′C的中点，则下列判断正确的序号是________．①四边形BFD′E在底面ABCD内的投影是正方形；②四边形BFD′E在平面A′D′DA内的投影是菱形；③四边形BFD′E在平面A′D′DA内的投影与在平面ABB′A内的投影是全等的平行四边形．答案：①③画空间几何体的三视图[例2]画出如右图所示的四棱锥的三视图．[解]几何体的三视图如下：[类题通法]画三视图的注意事项(1)务必做到长对正，宽相等，高平齐．(2)三视图的安排方法是正视图与侧视图在同一水平位置，且正视图在左，侧视图在右，俯视图在正视图的正下方．(3)若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法．[活学活用]沿一个正方体三个面的对角线截得的几何体如下图所示，则该几何体的侧视图为()答案：B由三视图还原空间几何体[例3]如下图所示的三视图表示的几何体是什么？画出物体的形状．(1)(2)(3)[解](1)该三视图表示的是一个四棱台，如右图．(2)由俯视图可知该几何体是多面体，结合正视图、侧视图可知该几何体是正六棱锥．如下图．(3)由于俯视图有一个圆和一个四边形，则该几何体是由旋转体和多面体拼接成的组合体，结合侧视图和正视图，可知该几何体上面是一个圆柱，下面是一个四棱柱，所以该几何体的形状如右图所示．[类题通法]由三视图还原几何体时，一般先由俯视图确定底面，由正视图与侧视图确定几何体的高及位置，同时想象视图中每一部分对应实物部分的形状．[活学活用]如图①、图②、图③、图④为4个几何体的三视图，根据三视图可以判断这四个几何体依次分别为()A．三棱台、三棱柱、圆锥、圆台B．三棱台、三棱锥、圆锥、圆台C．三棱柱、正四棱锥、圆锥、圆台D．三棱柱、三棱台、圆锥、圆台答案：C2.画几何体的三视图常见误区[典例]某几何体及其俯视图如下图所示，下列关于该几何体正视图和侧视图的画法正确的是()[解析]该几何体是由圆柱切割而得，由俯视图可知正视方向和侧视方向，进一步可画出正视图和侧视图(如图所示)，故选A.[答案] A[易错防范]1．易忽视该组合体的结构特征是由圆柱切割而得到，对正视方向与侧视方向的判断不正确而出错．2．三种视图中，可见的轮廓线都画成实线，存在但不可见的轮廓线一定要画出，但要画成虚线．画三视图时，一定要分清可见轮廓线与不可见轮廓线，避免出现错误．[成功破障]沿圆柱体上底面直径截去一部分后的物体如右图所示，它的俯视图是()答案：D一、选择题1．4个直立在地面上的字母广告牌在不同情况下，在地面上的投影(阴影部分)效果如图，则在字母L，K，C的投影中，与字母N属同一种投影的有()答案：A2.将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为()答案：D3．若某几何体的三视图如下图所示，则这个几何体的直观图可以是()答案：B4．某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()答案：C5．将正方体(如图①所示)截去两个三棱锥，得到图②所示的几何体，则该几何体的侧视图为()答案：B二、填空题6．已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于________．答案： 27．如图甲所示，在正方体ABCD -A1B1C1D1中，E，F分别是AA1，C1D1的中点，G是正方形BCC1B1的中心，则四边形AGFE在该正方体的各个面上的投影可能是图乙中的________．答案：(1)(2)(3)8．两条平行线在一个平面内的正投影可能是________．①两条平行线；②两个点；③两条相交直线；④一条直线和直线外的一点；⑤一条直线．答案：①②⑤三、解答题9．如下图所示，画出下列组合体的三视图．解：三视图如图①、图②所示．10．某组合体的三视图如下图所示，试画图说明此组合体的结构特征．解：该三视图表示的是组合体，如右图所示，是7个小正方体拼接而成的组合体．1．2.3空间几何体的直观图斜二测画法[导入新知]1．用斜二测画法画平面图形的步骤(1)在已知图形中取互相垂直的x轴和y轴，两轴相交于点O，画直观图时，把它们画成对应的x′轴和y′轴，两轴相交于点O′，且使∠x′O′y′＝45°(或135°)，它们确定的平面表示水平面．(2)已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴或y′轴的线段．(3)已知图形中平行于x轴的线段，在直观图中保持原长度不变，平行于y轴的线段，长度变为原来的一半．2．用斜二测画法画空间几何体的直观图的步骤(1)画底面，这时使用平面图形的斜二测画法即可．(2)画z′轴，z′轴过点O′，且与x′轴的夹角为90°，并画出高线(与原图高线相等，画正棱柱时只需要画侧棱即可)，连线成图．(3)擦去辅助线，被遮线用虚线表示．[化解疑难]1．画水平放置的平面图形的直观图，关键是确定多边形顶点的位置，借助于平面直角坐标系确定顶点后，只需把这些顶点顺次连接即可．2．用斜二测画法画直观图要掌握水平长不变，垂线长减半，直角画45°(或135°)．水平放置的平面图形的直观图[例1]按右图所示的建系方法，画水平放置的正五边形ABCDE的直观图．[解]画法：(1)在图①中作AG⊥x轴于G，作DH⊥x轴于H.(2)在图②中画相应的x′轴与y′轴，两轴相交于点O′，使∠x′O′y′＝45°.。

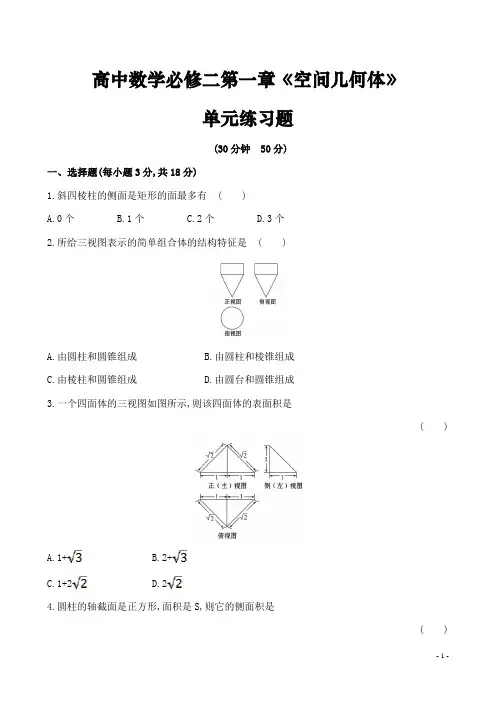
高中数学必修二第一章《空间几何体》单元练习题(30分钟50分)一、选择题(每小题3分,共18分)1.斜四棱柱的侧面是矩形的面最多有( )A.0个B.1个C.2个D.3个2.所给三视图表示的简单组合体的结构特征是( )A.由圆柱和圆锥组成B.由圆柱和棱锥组成C.由棱柱和圆锥组成D.由圆台和圆锥组成3.一个四面体的三视图如图所示,则该四面体的表面积是( )A.1+B.2+C.1+2D.24.圆柱的轴截面是正方形,面积是S,则它的侧面积是( )A.SB.πSC.2πSD.4πS5.若圆台两底面周长的比是1∶4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是 ( )A.B.C.1D.6.如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是 ( )二、填空题(每小题4分,共12分)7.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.8.在三棱柱ABC-A 1B 1C 1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P 分别是AB,BC,B 1C 1的中点,则三棱锥P-A 1MN 的体积是 .9.用一张4×8(cm 2)的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是 cm 2.三、解答题(每小题10分,共20分)10.已知四棱锥P-ABCD,其三视图和直观图如图,求该四棱锥的体积.11.如图所示,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的体积是多少?高中数学必修二第一章《空间几何体》单元练习题(30分钟50分)一、选择题(每小题3分,共18分)1.斜四棱柱的侧面是矩形的面最多有( )A.0个B.1个C.2个D.3个【解析】选C.根据棱柱的结构特征不可能有奇数个,因此最多2个.2.所给三视图表示的简单组合体的结构特征是( )A.由圆柱和圆锥组成B.由圆柱和棱锥组成C.由棱柱和圆锥组成D.由圆台和圆锥组成【解析】选A.由三视图可知此组合体的上方是圆柱,下方是圆锥,故选A.3.(2015·安徽高考)一个四面体的三视图如图所示,则该四面体的表面积是( )A.1+B.2+C.1+2D.2【解析】选B.由该四面体的三视图可知,该四面体的直观图如图所示:其中侧面PAC⊥底面ABC,且△PAC≌△BAC,由三视图中所给数据可知PA=PC=AB=BC=,取AC的中点O,连接PO,BO,则在Rt△POB中,PO=BO=1,可得PB=,所以S=2××2+×2×2=2+.4.(2015·西安高一检测)圆柱的轴截面是正方形,面积是S,则它的侧面积是( )A.SB.πSC.2πSD.4πS【解析】选B.设圆柱底面半径为r,则S=4r2,S侧=2πr·2r=4πr2=πS.5.若圆台两底面周长的比是1∶4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是( )A. B. C.1 D.【解析】选D.设上、下底半径分别为r1,r2,过高中点的圆面半径为r0,由题意得r2=4r1,r0=r1,所以==.6.(2015·威海高一检测)如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是( )【解析】选C.当俯视图为A中正方形时,几何体为棱长为1的正方体,体积为1;当俯视图为B中圆时,几何体为底面半径为,高为1的圆柱,体积为;当俯视图为C 中三角形时,几何体为三棱柱,且底面为直角边长为1的等腰直角三角形,高为1,体积为;当俯视图为D 中扇形时,几何体为圆柱的,且体积为. 二、填空题(每小题4分,共12分)7.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.【解析】设球的半径为rcm,则πr 2×8+πr 3×3=πr 2×6r.解得r=4. 答案:48.(2015·四川高考)在三棱柱ABC-A 1B 1C 1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P 分别是AB,BC,B 1C 1的中点,则三棱锥P-A 1MN 的体积是 .【解析】V=××=.答案:9.用一张4×8(cm 2)的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是 cm 2.【解析】以4为高卷起,则2πr=8,所以2r=,所以轴截面面积为cm 2;若以8为高卷起,则2πR=4,所以2R=,所以轴截面面积为cm 2.答案:三、解答题(每小题10分,共20分)10.已知四棱锥P-ABCD,其三视图和直观图如图,求该四棱锥的体积.【解析】由三视图知底面ABCD为矩形,AB=2,BC=4.顶点P在面ABCD内的射影为BC中点E,即棱锥的高为2,则体积V P-ABCD=S ABCD×PE=×2×4×2=.11.如图所示,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的体积是多少?【解析】设球半径为Rcm,根据已知条件知正方体的上底面与球相交所得截面圆的半径为4cm,球心到截面的距离为(R-2)cm,所以由42+(R-2)2=R2,得R=5,所以球的体积V=πR3=π×53=(cm3).。

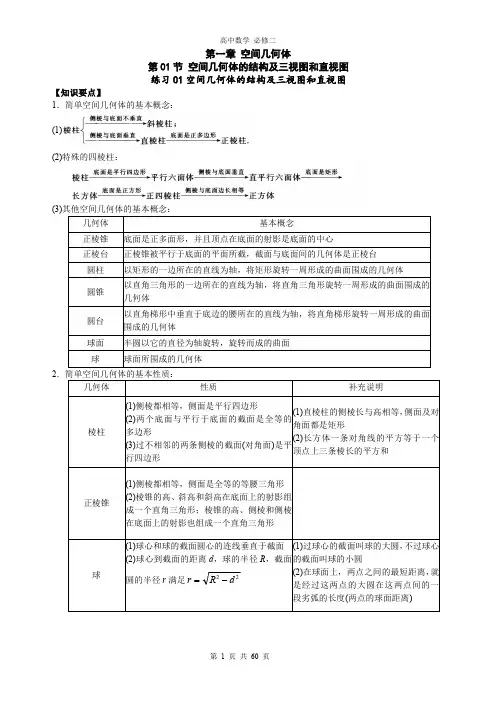
空间几何体的结构基础巩固1．下列说法正确的是()A．棱柱的底面一定是平行四边形B．棱锥的底面一定是三角形C．棱锥被平面分成的两部分不可能都是棱锥D．棱柱被平面分成的两部分可能都是棱柱解析：棱柱和棱锥的底面可以是任意多边形，故A、B错误；可沿棱锥的侧棱将其分割成两个棱锥，故C错误；用平行于棱柱底面的平面可将棱柱分割成两个棱柱，故D正确．答案：D2．具备下列条件的多面体是棱台的是()A．两底面是相似多边形的多面体B．侧面是梯形的多面体C．两底面平行的多面体D．两底面平行，侧棱延长后交于一点的多面体解析：四棱台、五棱柱、长方体各表面均为平面，是多边形，均为多面体，圆锥体的侧面为曲面，底面是圆，均不是多边形，因此不是多面体．故选D.答案：D3．等腰三角形ABC绕底边上的中线AD所在的直线旋转所得的几何体是()A．圆台B．圆锥C．圆柱D．球解析：由题意可得AD⊥BC，且BD＝CD，所以形成的几何体是圆锥．故选B.答案：B4．下列说法正确的有()①球的半径是球面上任意一点与球心的连线；②球的直径是球面上任意两点间的线段；③用一个平面截一个球，得到的是一个圆；④用一个平面截一个球，得到的截面是一个圆面．A．0个B．1个C．2个D．3个解析：①是正确的；②是错误的，只有两点的连线经过球心时才为直径；③是错误的；④是正确的．答案：C5．图1中的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则截面图形可能是()图1A．(1)(2)B．(1)(3)C．(1)(4)D．(1)(5)解析：当截面不过旋转轴时，截面图形是(5)，故选D.答案：D6．下列说法正确的是()①圆台可以由任意一个梯形绕其一边所在直线旋转形成；②在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；③圆柱的任意两条母线平行，圆锥的任意两条母线相交，圆台的任意两条母线延长后相交．解析：①错，圆台是直角梯形绕其直角边所在直线或等腰梯形绕其底边的中线所在直线旋转形成的；由母线的定义知②错，③对．答案：③能力提升1．关于如图2所示几何体的正确说法为()图2①这是一个六面体②这是一个四棱台③这是一个四棱柱④此几何体可由三棱柱截去一个三棱柱得到⑤此几何体可由四棱柱截去一个三棱柱得到A．①②③ B.①③④C．①②④⑤ D.①③④⑤解析：①正确．因为有六个面，属于六面体的范围．②错误．因为侧棱的延长线不能交于一点，所以不正确．③正确．如果把几何体放倒就会发现是一个四棱柱．④⑤都正确．如图3所示．图3答案：D2．一个三棱锥，如果它的底面是直角三角形，那么它的三个侧面()A．至多有一个是直角三角形B．至多有两个是直角三角形C．可能都是直角三角形图4D．必然都是非直角三角形解析：注意到答案特征是研究侧面最多有几个直角三角形，这是一道开放性试题，需要研究在什么情况下侧面的直角三角形最多．在如图4所示的长方体中，三棱锥A­A1C1D1的三个侧面都是直角三角形．答案：C3．已知正四棱锥V­ABCD中，底面面积为16，侧棱的长为211，则该棱锥的高是________．解析：如图5，取正方形ABCD的中心O，连接VO、AO，则VO 就是正四棱锥V­ABCD的高．图5因为底面面积为16，所以AO ＝2 2.因为侧棱的长为211，所以VO ＝VA 2－AO 2＝44－8＝6.所以正四棱锥V ­ABCD 的高为6.答案：64．圆台的两底面半径分别为2，5，母线长是310，则其轴截面面积是________．解析：设圆台的高为h ，则h ＝（310）2－（5－2）2＝9，∴轴截面面积S ＝12(4＋10)×9＝63.答案：635．把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1∶4，母线长是10cm ，则圆锥的母线长为________．图6解析：如图6，设圆锥的母线长为y ，圆台的上、下底面半径为x ，4x ，根据相似三角形的比例关系得y －10y＝x 4x ，也就是4(y －10)＝y ，所以y ＝403cm ，所以圆锥的母线长为403cm.答案：403cm 6．下列说法中，正确的有________个．①有一个面是多边形，其余各面都是三角形的几何体是棱锥；②正棱锥的侧面是等边三角形；③底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．解析：图7①错误．棱锥的定义是：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥．而“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”，故此说法是错误的．如图7所示的几何体满足此说法，但它不是棱锥，理由是△ADE 和△BCF 无公共顶点．②错误．正棱锥的侧面都是等腰三角形，不一定是等边三角形．③错误．由已知条件知，此三棱锥的三个侧面未必全等，所以不一定是正三棱锥．如图8所示的三棱锥中有AB＝AD＝BD＝BC＝CD.满足底面△BCD为等边三角形，三个侧面△ABD，△ABC，△ACD都是等腰三角形，但AC长度不一定，三个侧面不一定全等．答案：07．直角三角形ABC中，AB＝3，BC＝4，AC＝5，分别以AB，BC，AC所在直线为轴旋转一周，分析所形成的几何体的结构特征．解：在Rt△ABC中，分别以三条边AB，BC，AC所在直线为轴旋转一周所得的几何体，如图9.图9其中图(1)和图(2)是两个不同的圆锥，它们的底面分别是半径为4和3的圆面，母线长均为5.图(3)是由两个同底圆锥构成的几何体，在圆锥AO中，AB为母线，在圆锥CO中，CB为母线．8．指出图中的三个几何体分别是由哪些简单几何体组成的．解：(1)几何体由一个圆锥、一个圆柱和一个圆台拼接而成．(2)几何体由一个六棱柱和一个圆柱拼接而成．(3)几何体由一个球和一个圆柱中挖去一个以圆柱下底面为底面、上底面圆心为顶点的圆锥拼接而成．拓展要求1．如图11，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是()图11A．棱柱B．棱台C．棱柱与棱锥的组合体D．不能确定解析：如图12.图12∵平面AA1D1D∥平面BB1C1C，∴有水的部分始终有两个平面平行，而其余各面都易证是平行四边形(水面与两平行平面的交线)，因此呈棱柱形状．答案：A2．已知圆锥的底面半径为r ，高为h ，正方体ABCD ­A 1B 1C 1D 1内接于圆锥，求这个正方体的棱长．解：图13过内接正方体的体对角线作圆锥的轴截面，如图13.设圆锥内接正方体的棱长为x ，则在轴截面中，正方体的对角面A 1ACC 1的一组邻边的长分别为x 和2x .因为△VA 1C 1∽△VMN ，所以A 1C 1MN ＝VO 1VO ，即2x 2r ＝h －x h，所以2hx ＝2rh －2rx ，即x ＝2rh 2r ＋2h.故这个正方体的棱长为2rh 2r ＋2h.。

AB D E F第一章 空间几何体综合型训练一、选择题1． 如果一个水平放置的图形的斜二测直观图是一个底面为045，腰和上底均为1的等腰梯形，那么原平面图形的面积是（ ）A ． 22+B ． 221+ C ． 222+ D ． 21+ 2． 半径为R 的半圆卷成一个圆锥，则它的体积为（ ）A ． 33RB ． 33RC ． 35RD ． 35R 3． 一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（ ）Ａ． 28cm π Ｂ． 212cmπ Ｃ． 216cm π Ｄ． 220cm π 4． 圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（ ）A ． 7 Ｂ． 6 Ｃ． 5 Ｄ． 35． 棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( )A ． 1:7 Ｂ． 2:7 Ｃ． 7:19 Ｄ． 5:166． 如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，//EF AB ,32EF =,且EF 与平面ABCD 的距离为2，则该多面体的体积为（ ） A ． 92Ｂ． 5 Ｃ． 6 Ｄ． 152 二、填空题1． 圆台的较小底面半径为1，母线长为2，一条母线和底面的一条半径有交点且成060,则圆台的侧面积为____________．2． Rt ABC ∆中，3,4,5AB BC AC ===，将三角形绕直角边AB 旋转一周所成的几何体的体积为____________．3． 等体积的球和正方体,它们的表面积的大小关系是S 球___S 正方体4． 若长方体的一个顶点上的三条棱的长分别为3,4,5，从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,其最短路程是______________．5． 图（1）为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成;图（2）中的三视图表示的实物为_____________．6． 若圆锥的表面积为a 平方米，且它的侧面展开图是一个半圆，则这个圆锥的底面的直径为_______________．三、解答题1． 有一个正四棱台形状的油槽，可以装油190L ，假如它的两底面边长分别等于60cm 和40cm ，求它的深度为多少cm ？2． 已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长．参考答案图（1） 图（2）一、选择题1． A恢复后的原图形为一直角梯形1(11)222S =⨯=+ 2． A2312,,,22324R r R r h V r h R πππ===== 3． B正方体的顶点都在球面上，则球为正方体的外接球，则2R =，2412R S R ππ===4． A (3)84,7S r r l r ππ=+==侧面积5． C 中截面的面积为4个单位， 12124746919V V ++==++ 6． D 过点,E F 作底面的垂面，得两个体积相等的四棱锥和一个三棱柱，1313152323234222V =⨯⨯⨯⨯+⨯⨯⨯= 二、填空题1． 6π 画出圆台，则12121,2,2,()6r r l S r r l ππ====+=圆台侧面2． 16π 旋转一周所成的几何体是以BC 为半径，以AB 为高的圆锥，2211431633V r h πππ==⨯⨯= 3． <设334,3V R a a R π====2264S a S R π=====<正球4．从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,有两种方案==5． （1）4 （2）圆锥6．设圆锥的底面的半径为r ，圆锥的母线为l ，则由2l r ππ=得2l r =， 而22S r r r a ππ=+⋅=圆锥表，即23,r a r π===，即直径为3π三、解答题1.解：'1(),3V S S h h =+= 319000075360024001600h ⨯==++数学试卷及试题2．解：2229(25)(25),7l lππ+=+=。

人教新课标A版高中数学必修2 第一章空间几何体 1.1空间几何体的结构同步训练A卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题；共30分)1. （2分） (2018高一上·阜城月考) 轴截面为正方形的圆柱的侧面积与全面积的比是（）A . 2：3B . 4：9C . 3：2D . 4：12. （2分） (2016高一下·吉林期中) 下列命题中正确的是（）A . 正方形的直观图是正方形B . 平行四边形的直观图是平行四边形C . 有两个面平行，其余各面都是平行四边行的几何体叫棱柱D . 用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台3. （2分） (2016高二上·金华期中) 已知正四棱台的高是12cm，两底面边长之差为10cm，表面积为512cm2 ，则下底面的边长为（）A . 10B . 12C . 14D . 164. （2分）如图，长方体ABCD﹣A1B1C1D1被两平面分成三部分，其中EF∥GH∥BC，则这三个几何体中是棱柱的个数为（）A . 0B . 1C . 2D . 35. （2分）已知圆锥的母线长与底面半径长之比为3：1，一个正方体有四个顶点在圆锥的底面内，另外的四个顶点在圆锥的侧面上（如图），则圆锥与正方体的表面积之比为（）A . π：1B . 3π：1C . 3π：2D . 3π：46. （2分）如图，四边形ABCD中，AB=AD=CD=1，，.将四边形ABCD沿对角线BD折成四面体，使平面平面BCD，则下列结论正确的是A .B .C . 与平面所成的角为D . 四面体的体积为7. （2分）下列关于棱柱的说法中，错误的是（）A . 三棱柱的底面为三角形B . 一个棱柱至少有五个面C . 若棱柱的底面边长相等，则它的各个侧面全等D . 五棱柱有5条侧棱、5个侧面，侧面为平行四边形8. （2分）(2018·中山模拟) 如图，网格纸上正方形小格的边长为1（表示1cm）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A .B .C .D .9. （2分） (2019高一上·中山月考) 下列说法不正确的是（）A . 三角形一定是平面图形B . 若四边形的两对角线相交于一点，则该四边形是平面图形C . 圆心和圆上两点可确定一个平面D . 三条平行线最多可确定三个平面10. （2分）一个凸多面体的各个面都是四边形，它的顶点数是16，则它的面数为（）A . 14B . 7C . 15D . 不能确定11. （2分）下面多面体是五面体的是（）A . 三棱锥B . 三棱柱C . 四棱柱D . 五棱锥12. （2分）过正棱台两底面中心的截面一定是（）A . 直角梯形B . 等腰梯形C . 一般梯形或等腰梯形D . 矩形13. （2分）如图，一个三棱柱形容器中盛有水，且侧棱AA1=8.若侧面AA1B1B水平放置时，液面恰好过AC ，BC ， A1C1，B1C1的中点.则当底面ABC水平放置时，液面高为（）A . 4B . 5C . 6D . 714. （2分）已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值为（）A .B .C .D .15. （2分）若一个圆锥的轴截面是等边三角形，则该圆锥的侧面积与底面积的比等于（）A . 3B . 2C .D .二、填空题 (共5题；共5分)16. （1分） (2019高一上·周口期中) 一个几何体的主视图为一个三角形，则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号)．①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱．17. （1分） (2018高一下·衡阳期末) 已知长方体内接于球，底面是边长为的正方形，为的中点，平面，则球的表面积为________．18. （1分）(2018·安徽模拟) 如图1所示是一种生活中常见的容器，其结构如图2，其中是矩形，和都是等腰梯形，且平面，现测得 ,与间的距离为，则几何体的体积为________ ．19. （1分）圆锥的底面半径为5cm，高为12cm，当它的内接圆柱的底面半径为________ 时，圆锥的内接圆柱全面积有最大值．20. （1分）螺母是由________和________两个简单几何体构成的．三、解答题 (共5题；共25分)21. （5分）已知圆C和y轴相切，圆心在直线x﹣3y=0上，且被直线y=x截得的弦长为（1）求圆C的方程．（2）若圆心在第一象限，求过点（6，5）且与该圆相切的直线方程．22. （5分）如图，在正方体ABCD﹣A1B1C1D1中，E，F，G，M，N分别是B1C1 ， A1D1 ， A1B1 ， BD，B1C 的中点，求证：（1）MN∥平面CDD1C1．（2）平面EBD∥平面FGA．23. （5分）如图是表示以AB=4，BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体，其中四边形EFGH为截面．已知AE=5，BF=8，CG=12．（1）作出截面EFGH与底面ABCD的交线l；（2）截面四边形EFGH是否为菱形？并证明你的结论；（3）求DH的长．24. （5分） (2017高一下·彭州期中) 圆台的一个底面周长是另一个底面周长的3倍，它的轴截面面积是392cm2 ，母线与轴的夹角是45°，求这个圆台的高、母线和两底面的半径．25. （5分）如图，直三棱柱ABC﹣A′B′C′，∠BAC=90°，AB=AC=， AA′=1，点M，N分别为A′B和B′C′的中点．（Ⅰ）证明：MN∥平面A′ACC′；（Ⅱ）求三棱锥A′﹣MNC的体积．（椎体体积公式V=Sh，其中S为底面面积，h为高）参考答案一、单选题 (共15题；共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题；共5分) 16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题；共25分) 21-1、22-1、22-2、23-1、24-1、25-1、。

高一数学必修二第一章空间几何形状练习题及答案练题1. 已知立方体$ABCD-A_1B_1C_1D_1$的棱长为$6\text{cm}$ ，点$E$恰好在 $BC$ 上，在 $DE$ 上取点 $F$，试求：(1) $\angle A_1FB_1$ 的大小；(2) $EF$ 的长度。

2. 已知底面为等腰直角梯形的四面体$S-ABC$，$AB=AC=\sqrt{3}\text{cm}$，$BC=2\text{cm}$，$SA\perp AB$，$SA=2\text{cm}$，$M$ 为 $BC$ 中点，过点 $M$ 作 $SA$ 的垂线$MH$，交 $BC$ 于点 $H$。

(1)求 $SA$ 与面 $ABC$ 的夹角；(2) 求 $MH$ 的长度。

3. 在正四面体$S-ABC$中，$M$ 为 $BC$ 中点，过 $S$，$M$ 的平面与直线 $AB$ 交于点 $E$，过 $S$，$M$ 的平面与直线$BC$ 交于点 $F$。

(1) 求 $EF$ 的长；(2) 设 $SE$ 交 $AF$ 于 $N$，求 $SN$ 的长。

4. 已知棱长为 $5\text{cm}$ 的正四棱锥 $S-ABCD$，平面$ABCD$ 与平面 $SAB$ 的夹角为 $60^{\circ}$。

设 $AD$ 与平面$SBC$ 相交于 $E$，$BE$ 交平面 $SAD$ 于点 $F$。

(1) 求过顶点 $S$ 的平面与平面 $ABCD$ 的交线段的长度；(2) 过顶点 $S$ 且垂直于平面 $ABCD$ 的直线交 $EF$ 于点$G$，求 $SG$ 的长度。

答案1.(1) $\angle A_1FB_1=45^{\circ}$(2) $EF=3\sqrt{2}\text{cm}$2.(1) $\cos \angle BSA=\dfrac{\sqrt{2}}{2}$, 则 $\angle BSA=45^{\circ}$。

(2) $MH=\dfrac{\sqrt{2}}{2}\text{cm}$3.(1) $EF= \dfrac{5\sqrt{3}}{3}$(2) $SN=\dfrac{5\sqrt{2}}{6}$4.(1) $SB=\dfrac{5\sqrt{3}}{2}$(2) $SG=\dfrac{5\sqrt{3}}{6}$以上答案仅供参考，具体求解过程需要参考相关知识点及公式计算。

高中数学必修二第一章空间几何体的构造练习题必修二第一章空间几何体的构造()1．以下几何体中棱柱有A．5个 B ． 4个C．3 个个D ．22．有两个面平行的多面体不可能是()B．棱锥A．棱柱C．棱台D．以上都错3．一棱柱有 10 个极点，且全部侧棱长之和为100，则其侧棱长为 ()B．20A．10C．5D．154．以下命题中正确的选项是 ()A．用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台B．两个底面平行且相像，其余各面都是梯形的多面体是棱台C．棱台的底面是两个相像的正方形D．棱台的侧棱延伸后必交于一点5．面数最少的棱柱为 ________棱柱，共由 ________个面围成．分析：棱柱有互相平行的两个底面，其侧面起码有 3 个，故面数最少的棱柱为三棱柱，共有五个面围成．6.如图，正方形ABCD中，E，F分别为CD，BC 的中点，沿 AE，AF，EF 将其折成一个多面体，则此多面体是 ______________．7．如图，这是一个正方体的表面睁开图，把它再折成正方体 .有以下命题：R 重①点 H 与点 C 重合；②点 D 与点 M、点合；③点 B 与点 Q 重合；④点 A 与点 S重合．此中 ,正确命题的序号是 ________．(注：把你认为正确的命题的序号都填上)8．在一个长方体的容器中，装有少许水 .现将容器绕着其底部的一条棱倾斜，在倾斜的过程中,(1)水面的形状不停变化，可能是矩形，也可能变为不是矩形的平行四边形，对吗？(2)水的形状也不停变化，能够是棱柱，也可能变为棱台或棱锥，对吗？(3)假如倾斜时，不是绕着底部的一条棱，而是绕着其底部的一个极点，上边的第 (1)题和第 (2)题对不对？9．对于四周体ABCD，以下命题正确的选项是 ________(写出全部正确命题的编号 )．①相对棱 AB 与 CD 所在的直线是异面直线；②由极点 A 作四周体的高，其垂足是△ BCD 三条高线的交点；③若分别作△ ABC 和△ ABD 的边 AB 上的高，则这两条高的垂足重合；④任何三个面的面积之和都大于第四个面的面积；⑤分别作三组相对棱中点的连线，所得的三条线段订交于一点．10.右图是由哪个平面图形旋转得到的()11．以钝角三角形的较小边所在的直线为轴，其余两边旋转一周所获得的几何体是()A．两个圆锥拼接而成的组合体B．一个圆台C．一个圆锥D．一个圆锥挖去一个同底的小圆锥12．给出以下命题：①在圆柱的上、下两底面的圆周上各取一点，则这两点的连线是圆柱的母线；②圆锥的极点与底面圆周上随意一点的连线是圆锥的母线；③在圆台上、下两底面的圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的随意两条母线互相平行．此中正确的选项是 ()A．①②B．②③C．①③ D ．②④13.给出以下图的几何体，对于其构造特征，以下说法不．正确的选项是 ()的A．该几何体是由两个同底的四棱锥构成几何体B．该几何体有 12 条棱、 6 个极点C．该几何体有 8 个面，而且各面均为三角形D ．该几何体有 9 个面，此中一个面是四边形，其余均为三角形14．给出以下 7 种几何体：(1)柱体有 ________；(2)锥体有 ________；(3)球有 ________；(4)棱柱有 ________；(5)圆柱有 ________；(6)棱锥有 ________；(7)圆锥有 ________．15．已知ABCD为等腰梯形，两底边为AB，CD，且 AB ＞CD，绕 AB 所在直线旋转一周，所形成的几何体是由________和________构成的组合体．斜二测画法．正确的选项是 ()1．对于斜二测画法，以下说法不′A．原图形中平行于x轴的线段，其对应线段平行于x轴，长度不变B．原图形中平行于y1 轴的线段，其对应线段平行于y′轴，长度变为本来的C．在画与直角坐标系2xOy对应的坐标系x′O′y′时，∠x′O′y′一定是45°D ．在画直观图时，因为选轴的不一样，所得的直观图可能不一样2．以下图为某一平面图形的直观图，则此平面图形可能是以下图中的 ()3．成立坐标系，获得两个正三角形 ABC 的直观图不是全等三角形的一组是 ()4.以下图的正方形O′A′B′C′，其边长为1cm，它是一个水平搁置的平面图形的直观图，则原图形的周长是()A．6 cmB．8 cm2) cmC．(2＋3D．(2＋23) cm5．如图，△A′B′C′是水平搁置的△ABC的斜二测直观图，已知 A′C′＝6，B′C′＝4，则 AB边的实质长度是 ________．6．以下图，一个水平搁置的正方形ABCO，在直角坐标系 xOy 中，点 B 的坐标为(2,2)，则在用斜二测画法画出的正方形的直观图中，极点 B′到 x′轴的距离为________．7．以下图，△ABC中，AC＝10 cm，边AC上的高BD＝10 cm，求其水平搁置的直观图的面积．8．用斜二测画法画出底面边长为 4 cm，高为 3cm 的正四棱锥 (底面是正方形，而且极点在底面的正射影是底面中心的棱锥 )的直观图．三视图1．以下图物体的三视图是()2．如图，几何体的正视图和侧视图都正确的选项是()3.(2011·新课标全国高考)在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图能够为()4．以下图，在这 4 个几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④5．以下图中三视图所表示几何体的名称为________．第5题图第 4题图6．以下图，点O为正方体ABCD-A′B′C′D′的中心，点E 为面B′BCC′的中心，点F 为B′C′的中点，则空间四边形 D′OEF 在该正方体的面上的正投影可能是________(填出全部可能的序号 )．7．说出图中的三视图表示的几何体，并画出它的表示图．8．以下图的几何体是由一个长方体木块锯成的．(1) 判断该几何体能否为棱柱；(2)画出它的三视图．9． (2011 ·广东高考)如图，某几何体的正视图是平行四边形，侧视图和俯视图都是矩形，则该几何体的体积为 ()A．183B．12 3C．93D．6 310． (2011 ·辽宁高考)一个正三棱柱的侧棱长和底面边长相等，体积为 23，它的三视图中的俯视图如图所示．左视图是一个矩形．则这个矩形的面积是 ________．B．2 3A．4C．2 D. 3立体几何三视图体积表面积一、选择题1．一个棱锥的三视图如图，则该棱2 2 锥的表面积为（）2（A）48 12 2（B）48 24 2正侧（C）72 12 2（D）72 24 22．某几何体的三视图以下图，则该几何体的体积为（）俯2248（D ）（A）（B）（C）3343．一个几何体的三视图如图，则其体积为（）A．20B．6C．16D．5334．一个四棱锥的三视图以下图，其侧视图是等边三角形．该四棱锥的体积等于（）A．3B．2 3C．3 3D．6 3正视图侧视图俯视图5．某四周体的三视图以下图，正视图、侧视图、俯视图都是边长为 1 的正方形，则此四周体的外接球的体积为（）A．C．4B ．3 32 D．36．某三棱锥的三视图以下图，该三棱锥的体积是为（）A．80B．40C．803 D．403示，则7．某几何体的三视图以以下图所该几何体的体积为（A） 200+9 π（B） 200+18 π（C） 140+9 π（D） 140+18 π8．若某几何体的三视图以下图，则此几何体的直观图是（）112A B正视图2侧（左）视图11俯视图C D9．某几何体的三视图以下图，则该几何体的体积为A．2B．2 2C． D ．23310．以下图是一个几何体的三视图，则这个几何体外接球的表面积为（）A ． 8B． 16C．32D．64二、填空题11．一个四棱柱的三视图以下图，则其体积为 _______．12．若某几何体的三视图如右图所示，则此几何体的体积是 ______.13．若某多面体的三视图如右图所示，则此多面体的体积为，外接球的表面积为．14．一个正三棱柱的三视图以下图 (单位：cm)，求这个正三棱柱的表面积与体积．15..如图，已知六棱锥P-ABC此中底面ABCDEF 是正六边形，点 P 在底面的投影是正六边形的中心，底面边长为 2 cm，侧棱长为 3cm，求六棱锥P-ABCDEF的表面积和体积．球1．长方体的一个极点上三条棱的长分别是 3、4、5，且它的八个极点都在同一个球面上，则这个球的表面积为()B．25 2πA.22πC． 50 πD． 200 π2．两个球的体积之比为8∶27，那么这两个球的表面积之比为 ()A．2∶3B．4∶9C.2∶3D. 8∶ 273． (2011 ·湖南高考)设以下图是某几何体的三视图，则该几何体的体积为()A． 9π＋42B． 36 π＋1899C.2π＋12D.2π＋184．假如一个球的外切圆锥的高是这个球的半径的 3 倍，则圆锥的侧面面积和球的表面积之比为()A．4∶3B．3∶1C．3∶2D．9∶45．已知OA为球O的半径，过OA的中点M，且垂直于OA 的平面截球面获得圆 M.若圆 M 的面积为3π，则球 O 的表面积等于 ________．6．以以下图，一个底面半径为R的圆柱形量杯中装有适当的水．放入一个半径为 r 的实心铁球，球被水吞没，高度R恰巧高升 r，则r＝________.7．某几何体的三视图以下图(单位：m)．(1)求该几何体的表面积；(2)求该几何体的体积．8．圆锥的底面半径为 3，母线长为 5，求它的内切球的表面积与体积．9． (2011 ·重庆高考)高为2的四棱锥S-ABCD的底面是边长为 1 的正方形，点S，A，B，C，D均在半径为1 的同一球面上，则底面ABCD 的中心与极点S 之间的距离为()102＋ 3A. 2B.23C.2D. 210．如图，半径为 2 的球O中有一内接圆柱，当圆柱的轴截面为正方形时球的表面积与圆柱的侧面积之差为________．。