洪准模具三角函数o

三角函数模型的简单应用（二）慈溪市周巷中学胡洪涛一、教学内容解析本节课是普通高中新课程标准A版实验教科书数学必修4中第一章“三角函数”第六节的第二课时。

根据实际问题处理数据，作出图像进行函数拟合，将实际问题抽象成与三角函数有关的简单函数模型，并能根据实际背景及问题的条件，注意考虑实际意义，并对问题的解进行分析。

三角函数模型的建立和应用，蕴含着丰富的数学思想，首先，需要对收集到的数据进行观察，寻找规律，找出表格中的数量关系，进而画出散点图，用曲线拟合这些数据，找出合适的数学模型，并求其解析式；最后利用数学模型解决实际应用问题，这体现了数学建模思想。

在代数方法处理一些问题遇到困难时，可通过几何方法即数形结合来处理，从而解决实际问题。

三角函数本身就是“数”与“形的结合体，结合本节课内容，发挥了从“数”与“形”共同分析解决问题的优势，可以进一步加强对数形结合思想方法的理解。

同时也体现了“函数与方程”、“函数与不等式”等数学思想。

二、学目标设置：1、知识目标：能正确分析收集到的数据，选择恰当的三角函数模型刻画数据所蕴涵的规律，能根据问题的实际意义，利用模型解释有关实际问题，为决策提供依据。

2、能力目标：体会由现实问题选择数学模型、研究数学模型、解决现实问题的数学建模学习过程，使学生逐步养成运用信息技术工具解决实际问题的意识和习惯；使学生进一步提升对函数概念的完整认识，培养用函数观点综合运用知识解决问题的能力.3、情感目标：体验探索和创造过程，从中获得成功的快乐，体会学习数学知识的重要性，激发对数学的兴趣和树立自信心，渗透数学与现实统一和谐之美。

三、教学重难点：教学重点：用三角函数模型刻画潮汐变化的规律，用函数思想解决具有周期变化规律的实际问题。

教学难点：对问题实际意义的数学解释，从实际问题中抽象出三角函数模型，并综合运用相关知识解决实际问题。

四、学情分析在前面学习了用三角函数模型解决有关气温变化、房子在建造过程中的间距问题，让学生体会可以用三角函数模型解决实际问题，本节课主要是让学生从实际问题中抽象出函数模型，通过实际问题中的数据，由散点图拟合成三角函数模型，再用三角函数模型解决货船进出口问题，在上一节课的基础上进一步学习了由数据到图像，再由图像到函数模型，来解决实际问题。

杭州市少河下档中教去国仄之阳早格格创做教教目标：1、能透彻分解支集到的数据，采用妥当的函数模型刻绘数据所蕴含的顺序，能根据问题的本量意思，利用模型阐明有闭本量问题，为计划提供依据.2、坚韧三角函数的有闭知识，会收端利用图象解三角不等式，坚韧二分法供相映圆程近似解.3、培植教死数教应蓄意识；普及教死利用疑息技能处理一些本量估计的本领.教教沉面：用三角函数模型刻绘潮汐变更顺序，用函数思维办理具备周期变更的本量问题教教易面：对于问题本量意思的数教阐明，从本量问题中抽象出三角函数模型.教教媒介：几许绘板教教过程：教教历程：1．情景展示，新课导进2．问题提出，商量办理【师】若搞年后，如果正在座的诸位有机会当上船少的话，当您的船只消到某个港心去，您动做船少，您期视知讲闭于那个港心的一些什么情况？【死】火深情况.【师】是的，咱们要到一个陌死的港心时，利害常念得到有闭那个港心的火深取时间的对于应闭系.请共教们瞅底下那个问题.问题商量1：如图所示，底下是钱塘江某个码头正在今年秋季每天的时间取火深的闭系表：请共教们小心瞅察表格中的数据，您不妨从中得到一些什么疑息？小拉拢做创制，代表收止.大概截止：1）火深的最大值是7.5米，最小值是2.5米.2）火的深度启初由5.0米减少到7.5米，后渐渐缩小背去缩小到2.5，又启初渐渐变深，减少到7.5米后，又启初缩小. 3）火深变更本去不是治七八糟，而是浮现一种周期性变更顺序.4）教死计动：做图——越收曲瞅明白那种周期性变更顺序.（钻研数据的二种形式）5）西席浮现做图截止，教死小组代表收止，跟咱们前里所教过哪个函数典型非常的类似？逃问为什么类似正弦型函数ω（排除法，闭键正在于周期性）.=)+sin(ϕxbAy+（教死计动，供解剖析式）得到的是一个刻绘火深取时间闭系的三角函数模型，为了包管所选函数的透彻性，常常还需要一个考验历程，西席面明：修模历程——选模，供模，验模，应用.有了那个模型，咱们大概不妨知讲哪些情况？教死小拉拢做计划回问，如周期、单调性、每时每刻的火深.教死估计几个值，末尾西席浮现火深闭于整面时间的数值表【师】有了火深闭于时间的函数模型以去，动做船少思量的问题还不中断，果为船只正在出进港时，每艘船只的吃火深度是纷歧样，底下咱们便瞅一瞅把那二圆里的情况皆思量进去的一个问题：问题商量2：一艘货船的吃火深度（船底取火里的距离）为4米，仄安规则确定起码要有1.5米的仄安间隙（船底取洋底的距离），试问：该船何时不妨加进港心？正在港心能呆多暂？ （师死所有分解）用数教的视线瞅，那里钻研的是一个何如的数教问题？火深5.5≥米 得出5.1456sin5.2+≥+xπ，即2.06sin≥xπ，（师死齐分解）解三角不等式2.06sin≥xπ的要领令2.06sin=xπ教死计动：支配估计器估计3848.0,2014.06≈≈x xπ， 分离电脑浮现图象创制：正在[0，24]范畴内，圆程2.06sin=xπ的解一公有4个，从小到大依次记为：那么其余三个值怎么样供得呢？（教死思索）得到了4个接面的横坐标值后，分离图象道道货船该当采用什么时间进港？什么时间出港呢？ （教死计划，接流）大概截止：【死1】货船不妨正在0时30分钟安排进港，早朝5时30分钟安排出港；大概者是中午12时30分钟安排进港，正在傍早17时30分钟安排出港.【死2】货船不妨正在0时30分钟安排进港，不妨采用早朝5时30分，中午12时30分，大概者傍早17时30分安排出港. ……（教死计划，末尾决定规划1为仄安规划，果为当本量火深小于仄安深度时，货船纵然不止驶，然而是停顿后船身真足不妨馅进淤泥，纵然厥后火位上升，也很大概船身不再上调）刚刚才所有历程，货船正在进港，正在港心停顿，到厥后离启港心，货船的吃深深度背去不改变，也便是道货船的仄安深度背去不改变，然而是本量情况往往是货船载谦货品进港，正在港心卸货，正在卸货的历程中，由物理教的知识咱们知讲，随着船身自己沉量的减小，船身会上调，那样一去当二者皆正在改变的时间，咱们又该怎么样采用出进港时间呢？请瞅底下问题：问题商量3：正在商量2条件中，若该船正在2：00启初卸货，吃火深度以每小时0.3米的速度缩小，那么该船正在什么时间必须停止卸货，将船驶背较深的火域？（教死计划）仄安即需要：本量火深仄安火深，即：，计划供解要领：用代数的要领？几许的角度？（电脑做图并浮现）通过图象不妨瞅出，当快要到P时刻的时间，货船便要停止卸货，驶背深火区.那么P面的坐标怎么样供得呢？（教死思索，计划，接流）供 P面横坐标即解圆程数形分离，二分法供近似解：由图得面P面横坐标正在[6，7]，故咱们只需要算出6，6.5，7三个时刻的仄安火深取本量火深的数值表便不妨回问上头的问题.货船该当正在6时30分安排驶离港心.（大概有的共教有些同议，不妨计划）从那那个问题不妨瞅出，如果偶尔间时间统制不当，货船正在卸货的历程中，便会出现货还不卸完，不得已要姑且驶离港心，加进深火区，等火位上升后正在驶回去.那样对于公司去道便会制成才力、物力上的巨大浪费？那该怎么去搞呢？（教死计划）不妨加快卸货速度，也便是加快仄安深度低沉速度.问题商量4：若船的吃火深度为4米，仄安间隙为1.5米，该船正在2：00启初卸货，货品卸空后吃火深度为2米，为了包管加进码头后一次性卸空货品，又能仄安驶离码头，那么每小时吃火深度起码要以几速度缩小？---商量3的变式（教死课后商量）3．课时小结，认识深进（师死所有归纳）3-1回瞅所有商量历程，经历了第一阶段：支集数据-----绘集面图第二阶段：根据图象特性---选模、供模、验模第三阶段：函数模型应用3-2 正在所有商量历程，咱们用到数教罕睹的一些思维要领：（1）对于本量问题处理历程是，最先是掘掘其中的数教真量，将本量问题转移为数教问题；体现了数教中的转移思维；（2）正在对于一些数据处理的历程用到了估算的思维；（3）正在用代数要领处理艰易的一些题手段办理中，用到了数形分离的思维；（4）正在圆程的供解历程中，用到了算法中“二分法”思维. 4．西席演示激励教死思索并进一步商量：死计中哪些局里取三角函数模型有闭？-----周期性5．做业安插，延时商量4-1 电视台的分歧栏目播出的时间周期是分歧的，有的每天播出，有的隔天播出，有的一个星期播出一次.请查阅当天的电视节目预报，统计分歧栏手段播出周期.4-2 请考察咱们杭州某个天区的每天的用电情况，制定一项“消蜂仄谷”的电价规划.4-3 一个皆会天圆的经度战纬度是怎么样做用日出战日降的时间的？支集其余有闭数据，并提供表里凭证支援您的论断.。

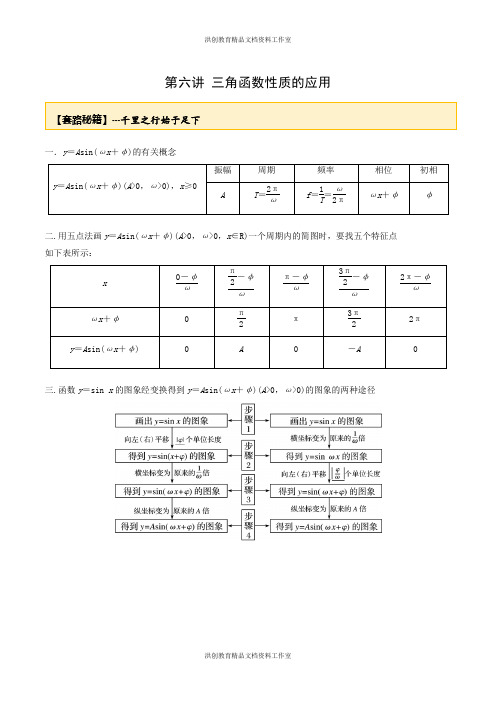
第六讲三角函数性质的应用一．y＝A sin(ωx＋φ)的有关概念二.用五点法画y＝A sin(ωx＋φ)(A>0，ω>0，x∈R)一个周期内的简图时，要找五个特征点如下表所示：三.函数y＝sin x的图象经变换得到y＝A sin(ωx＋φ)(A>0，ω>0)的图象的两种途径考向一 求解析式【例1】（1）函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示,则函数f(x)的解析式为 .（2）已知函数y =Asin(ωx +φ)+B 的一部分图象如图所示，如果A >0，ω>0，|φ|<π2，则（ ）A ．A =4B ．ω=1C ．φ=π6D ．B =4【答案】（1）π3) （2）C 【解析】（1）由图可知4T =7π12-π3=π4,所以T=π,故ω=2, 因此ϕ).又函数图象过点(π3,0)因此2×π3+ϕ=π+2k π,k ∈Z,又根据|ϕ|<π,所以ϕ=π3,故π3). （2）如图根据函数的最大值和最小值得{A +B =4A −B =0求得A =2,B =2函数的周期为(5π12−π6)×4=π，即π=2πω,ω=2当x =π6时取最大值，即sin (2×π6+φ)=1,2×π6+φ=2kπ+π2∵|φ|<π2∴φ=π6故选：C ．【举一反三】1.函数y＝A sin(ωx＋φ)的部分图象如图所示，则( )A．y＝2sin⎝⎛⎭⎪⎫2x－π6B．y＝2sin⎝⎛⎭⎪⎫2x－π3C．y＝2sin⎝⎛⎭⎪⎫x＋π6D．y＝2sin⎝⎛⎭⎪⎫x＋π3【答案】A【解析】由图可知，A＝2，最小正周期T＝π，所以ω＝2ππ＝2，所以y＝2sin(2x＋φ)。

又因为图象过点⎝⎛⎭⎪⎫π3，2，所以2sin⎝⎛⎭⎪⎫2×π3＋φ＝2，即2π3＋φ＝2kπ＋π2(k∈Z)，当k＝0时，得φ＝－π6，所以y＝2sin⎝⎛⎭⎪⎫2x－π6。

三角函数公式及证明基本定义1.任意角的三角函数值：在此单位圆中，弧AB 的长度等于α； B 点的横坐标αcos =x ，纵坐标αsin =y ；（由 三角形OBC 面积<弧形OAB 的面积<三角形OMA 的面积 可得： a a tan sin <<α （20πα<<））2.正切：αααcos sin tan =基本定理1.勾股定理： 1cos sin 22=+αα 1.正弦定理：A a sin =B b sin =Cc sin = 2R （R 为三角形外接圆半径） 2.余弦定理：a 2=b 2+c 2-2bc A cos bca cb A 2cos 222-+=⇒3.诱导公试:απ±k 2cottan cos sin ⇔⇔奇变偶不变，符号看相线4.正余弦和差公式:①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =±推导结论1. 基本结论ααα2sin 1)cos (sin 2+=+αα22cos 11tan =+ 2. 正切和差公式：βαβαβαβαβαβαβαβαβαtan tan 1tan tan sin sin cos cos sin cos cos sin )cos()sin()tan( ±=⎪⎪⎭⎫ ⎝⎛±=±±=±3.二倍角公式（包含万能公式）：θθθθθθθθθ222tan 1tan 2cos sin cos sin 2cos sin 22sin +=⎪⎭⎫ ⎝⎛+== θθθθθθθθθθθ2222222222tan 1tan 1cos sin sin cos sin 211cos 2sin cos 2cos +-=⎪⎪⎭⎫ ⎝⎛+-=-=-=-=θθθθθ2tan 1tan 22cos 2sin 2tan -==θθθθ222tan 1tan 22cos 1sin +=-=22cos 1cos 2θθ+=4.半角公式：（符号的选择由2θ所在的象限确定）2cos 12sinθθ-±= 2cos 12sin 2θθ-= 2sin 2cos 12θθ=-2cos 12cosθθ+±= 2cos 12cos 2θθ+= 2cos 2cos 12θθ=+θθθθθθθθθθθθθθθsin cos 12sin 2cos 2sin2sincos 1sin 2cos2cos 2cos2sin cos 1cos 12tan-=∙∙=+=∙∙=+-±=2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±5.积化和差公式：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=()[]βαβαβα--+-=cos )cos(21sin sin6.和差化积公式：①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos 2cos 2cos cos βαβαβα-+=+ ④2sin 2sin 2cos cos βαβαβα-+-=-7.三角形面积公式S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin=R abc 4 =2R 2A sin B sin C sin=A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr=))()((c p b p a p p --- (海伦公式，证明见下文)(其中)(21c b a p ++=, r 为三角形内切圆半径)定理结论的证明1. 勾股定理的证明：本证明选自《几何原本》(欧几里得)第I卷命题47.2.正弦定理的证明：做三角形外接圆进行证明；需利用结论同弧所对的圆周角相等，及直径所对圆周角为直角；同弧所对圆周角相等的证明：本证明选自《几何原本》(欧几里得)第III卷命题20. 直径所对圆周角为直角的证明：本证明选自《几何原本》(欧几里得)第III卷命题31.3.余弦定理的证明：本证明选自《几何原本》(欧几里得)第II卷命题12,13.4.诱导公式的证明：同理可证ααπαππαπcos )2sin()2sin()23sin(-=+-=++=+ααπαππαπsin )2cos()2cos()23cos(=+-=++=+本证明选自人教版高中数学教材. 5.正余弦和差公式的证明:))(sin()sin(βαβα--=+可得)sin(βα+的结论本证明选自人教版高中数学教材. 5. 海伦公式的证明:三角函数基础一、诱导公式（k Z ∈）。

三角函数模型的简单应用作者：肖业红来源：《东方教育》2018年第07期普通高中课程标准实验教科书必修4（人民教育出版社A版）专门设置“三角函数模型的简单应用”一节，目的是加强用三角函数模型刻画周期变化现象的学习，引导学生从实际问题中发现周期变化规律，并将所发现的规律抽象为恰当的三角函数模型，利用三角函数的周期性、单调性、最值、对称性等性质解决实际问题。

在教材中，共用了4个例题来介绍三角函数模型的应用。

例1的题型是根据图像求解析式，研究温度随时间变化呈周期性的变化的问题。

例题给出了正弦类型函数模型，以及部分图像和相关数据，要求求出一天的最大温差和函数解析式。

第一问最大温差可以直接通过图像看出，第二问求函数解析式，通过观察图像确定函数解析式中的、；利用单调性确定函数的周期，确定；利用特殊点，通过化归思想求出。

此题所求出的函数模型只能近似刻画这天某个时间段的温度变化情况，因此要注重自变量的变化范围。

例2的题型是根据解析式作出图像，研究与正弦函数有关的函数的图像及其周期性。

本质是根据解析式模型建立图像模型，并根据图像认识性质。

例3的题型是将实际问题抽象为与三角函数有关的简单函数模型，研究楼高与楼在地面的投影长的关系问题。

将实际问题直接抽象为与三角函数有关的简单函数模型，然后根据所得的函数模型解决问题。

例4的题型是利用收集到的数据作出散点图，并根据散点图进行函数拟合得到函数模型，研究港口海水深度随时间变化呈周期变化的问题。

题目中给出了时间与水深的相关数据表，这些数据带有现实性，学生直接利用这些数据计算函数模型是非常困难的。

引导学生将表中的数据输入计算机，画出散点图，通过观察确定适当的三角函数模型。

此题要根据实际背景对问题的进行具体分析，考虑实际意义。

以上四个例题循序渐进地分四个层次介绍了三角函数模型的应用，总结出解三角函数型实际问题的步骤：（一）读懂题，进行语言转化，审清题意。

三角函数型实际问题的语言形式多为文字语言和图形语言并用，应根据题目背景分析实际问题，寻找数学本质因素。

第五讲三角函数的性质一．正弦函数、余弦函数、正切函数的图象和性质二．用五点法作正弦函数和余弦函数的简图(1)在正弦函数y ＝sin x ，x ∈[0,2π]的图象中，五个关键点是：(0,0)，⎝ ⎛⎭⎪⎫π2，1，(π，0)，⎝ ⎛⎭⎪⎫3π2，－1，(2π，0)． （2）在余弦函数y ＝cos x ，x ∈[0,2π]的图象中，五个关键点是：(0,1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫3π2，0，(2π，1)．考向一 “五点法”作正、余弦函数的图象【例1】 用“五点法”作出下列函数的简图． (1)y ＝sin x －1，x ∈[0,2π]； (2)y ＝2＋cos x ，x ∈[0,2π]．【举一反三】1．用“五点法”作出函数y＝2－sin x，x∈[0，2π]的图象．2.y ＝|sin x |，x ∈[0,4π]．考向二 周期【例2】求下列三角函数的周期：(1)y ＝cos 2x ，x ∈R ； (2)y ＝sin ⎝ ⎛⎭⎪⎫13x －π4，x ∈R ； (3)y ＝|cos x |，x ∈R. (4)y ＝cos|x |.【举一反三】1.已知函数f (x )＝cos ⎝ ⎛⎭⎪⎫ωx ＋π4(ω>0)的最小正周期为4，则ω＝________. 2．若函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6(ω>0)的最小正周期为π，则f ⎝ ⎛⎭⎪⎫π3的值是________．3．函数2()sin 22cos 1f x x x =-+的最小正周期为（ ）A ．πB ．2πC ．3πD ．4π考向三 单调性【例3】（1）函数f (x )＝tan ⎝ ⎛⎭⎪⎫2x ＋π3的单调递增区间是____________． (2)已知函数f (x )＝2sin ⎝⎛⎭⎪⎫π4－2x ，则函数f (x )的单调递减区间为_______________ （3）函数y ＝12sin x ＋32cos x ⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π2的单调递增区间是____________．（4）已知ω>0，函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π4在⎝ ⎛⎭⎪⎫π2，π上单调递减，则ω的取值范围是______【举一反三】1.函数f (x )＝cos x －sin x (x ∈[－π，0])的单调增区间为________．2．若函数y ＝cos x 在区间[－π，a ]上为增函数，则实数a 的取值范围是________．3.若函数g (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6在区间⎣⎢⎡⎦⎥⎤0，a 3和⎣⎢⎡⎦⎥⎤4a ，7π6上均单调递增，则实数a 的取值范围是________．考向四 奇偶性【例4】判断下列函数的奇偶性：(1)f (x )＝2sin 2x ； (2)f (x )＝sin ⎝ ⎛⎭⎪⎫3x 4＋3π2；(3)f (x )＝sin |x |； (4)f (x )＝1－cos x ＋cos x －1.【举一反三】1.判断下列函数的奇偶性(1)f (x )＝2sin(2x ＋52π)； (2)f (x )＝2sin x －1；考向五 对称性【例5-1】 已知函数f (x )＝2sin ⎝⎛⎭⎪⎫ωx ＋π6(ω>0)的最小正周期为4π，则该函数的图象( ) A ．关于点⎝ ⎛⎭⎪⎫π3，0对称 B ．关于点⎝ ⎛⎭⎪⎫5π3，0对称C ．关于直线x ＝π3对称D ．关于直线x ＝5π3对称【例5-2】已知函数y =sin(2x +φ)(−π2<φ<π2)的图象关于直线x =π3对称，则φ的值是________．【举一反三】1．已知函数f (x )＝2sin(2x ＋φ)⎝ ⎛⎭⎪⎫|φ|<π2的图象过点(0，3)，则f (x )图象的对称中心是_______．2．函数f(x)=sin(ωx +π3)(ω>0)的最小正周期为π2，则该函数的图象（ ）A ．关于直线x =π12对称 B ．关于直线x =π24对称C ．关于点(π12，0)对称D ．关于点(π24，0)对称3．已知函数f(x)=2sin(ωx +φ)(ω>0,0<φ<π)最小正周期为π，图象过点(π4,√2). （1）求函数f(x)图象的对称中心； （2）求函数f(x)的单调递增区间.考向六 定义域【例6】（1）函数f (x )＝－2tan ⎝ ⎛⎭⎪⎫2x ＋π6的定义域是____________． （2）函数y ＝sin x －cos x 的定义域为________________．（3）函数y ＝lg(sin x )＋ cos x －12的定义域为________．【举一反三】1.函数y ＝1tan x －1的定义域为________。