2014年几何专题训练锐角三角函数和投影与视图

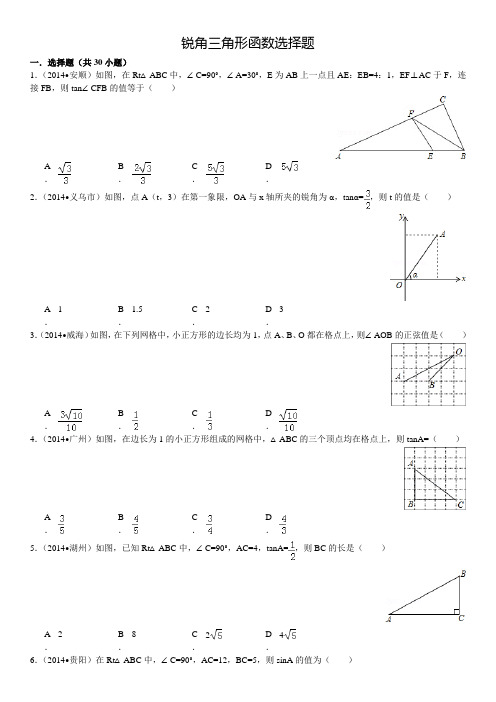
锐角三角形函数选择题一．选择题（共30小题）1．（2014•安顺）如图，在Rt△ABC中，∠C=90°，∠A=30°，E为AB上一点且AE：EB=4：1，EF⊥AC于F，连接FB，则tan∠CFB的值等于（）A ．B．C．D．2．（2014•义乌市）如图，点A（t，3）在第一象限，OA与x轴所夹的锐角为α，tanα=，则t的值是（）A ．1 B．1.5 C．2 D．33．（2014•威海）如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是（）A ．B．C．D．4．（2014•广州）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（）A ．B．C．D．5．（2014•湖州）如图，已知Rt△ABC中，∠C=90°，AC=4，tanA=，则BC的长是（）A ．2 B．8 C．2D．46．（2014•贵阳）在Rt△ABC中，∠C=90°，AC=12，BC=5，则sinA的值为（）A ．B．C．D．7．（2014•兰州）如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，那么cosA的值等于（）A ．B．C．D．8．（2014•巴中）在Rt△ABC中，∠C=90°，sinA=，则tanB的值为（）A ．B．C．D．9．（2014•天津）cos60°的值等于（）A ．B．C．D．10．（2014•厦门）sin30°的值是（）A ．B．C．D．111．（2014•包头）计算sin245°+cos30°•tan60°，其结果是（）A ．2 B．1 C．D．12．（2014•凉山州）在△ABC中，若|cosA﹣|+（1﹣tanB）2=0，则∠C的度数是（）A ．45°B．60°C．75°D．105°13．（2014•泰州）如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）A ．1，2，3 B．1，1，C．1，1，D．1，2，14．（2014•杭州）在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC=（）A ．3sin40°B．3sin50°C．3tan40°D．3tan50°15．（2014•滨州）在Rt△ACB中，∠C=90°，AB=10，sinA=，cosA=，tanA=，则BC的长为（）A ．6 B．7.5 C．8 D．12.516．（2014•连云港）如图，若△ABC和△DEF的面积分别为S1、S2，则（）A ．S1=S2B．S1=S2C．S1=S2D．S1=S217．（2014•随州）如图，要测量B点到河岸AD的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=100米，则B点到河岸AD的距离为（）A ．100米B．50米C．米D．50米18．（2014•丽水）如图，河坝横断面迎水坡AB的坡比是（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是（）A ．9m B．6m C．m D．m19．（2014•凉山州）拦水坝横断面如图所示，迎水坡AB的坡比是1：，坝高BC=10m，则坡面AB的长度是（）A ．15m B．20m C．10m D．20m20．（2014•衡阳）如图，一河坝的横断面为等腰梯形ABCD，坝顶宽10米，坝高12米，斜坡AB的坡度i=1：1.5，则坝底AD的长度为（）A ．26米B．28米C．30米D．46米21．（2014•德州）如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为（）A ．4米B．6米C．12米D．24米22．（2014•呼伦贝尔）如图，在水平地面上，由点A测得旗杆BC顶点C的仰角为60°，点A到旗杆的距离AB=12米，则旗杆的高度为（）A ．米B．6米C．米D．12米23．（2014•深圳）小明去爬山，在山脚看山顶角度为30°，小明在坡比为5：12的山坡上走1300米，此时小明看山顶的角度为60°，求山高（）A ．600﹣250B．600﹣250 C．350+350D．50024．（2014•西宁）如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，则二楼的层高BC约为（精确到0.1米，sin42°≈0.67，tan42°≈0.90）（）A ．10.8米B．8.9米C．8.0米D．5.8米25．（2014•百色）从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（）A ．（6+6）米B．（6+3）米C．（6+2）米D．12米26．（2014•临沂）如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为（）A ．20海里B．10海里C．20海里D．30海里27．（2014•绵阳）如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（）A ．40海里B．40海里C．80海里D．40海里28．（2014•苏州）如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（）A ．4km B．2km C．2km D．（+1）km29．（2013•昭通）如图，A、B、C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC′B′，则tanB′的值为（）A ．B．C．D．30．（2013•宿迁）如图，将∠AOB放置在5×5的正方形网格中，则tan∠AOB的值是（）A ．B．C．D．。

1．函数2cos ()4y x π=+的图象沿x 轴向右平移a 个单位(0)a >,所得图象关于y 轴对称,则a 的最小值为（ ） A ．πB ．34πC ．2πD ．4π2、已知ABC ∆中,三个内角A,B,C 的对边分别为a,b,c,若ABC ∆的面积为S,且()222,tan S a b c C =+-则等于A ．34B ．43C ．43-D ．34- 3、若,(,),tan cot ,2παβπαβ∈<且那么必有（ ）A ．2παβ+<B ．32αβπ+<C ．αβ>D ．αβ<4.直线1l 与2l 相交于点A ，动点B 、C 分别在直线1l 与2l 上且异于点A ，若AB 与AC 的夹角为60，BC = ，则ABC ∆的外接圆的面积为 A. 2π B. 4π C. 8πD. 12π5、设()()()cos 0,0,0f x A x A ωϕωϕπ=+>><<为奇函数，该函数的部分图象如图1所示，EFG ∆是边长为2的等边三角形，则)1(f 的值为A ．23- B ．26-C ．3 D ． 3-6.设向量cos 1,1)a θθ=++ ，(1,1)b = ，2[,]33ππθ∈，m 是向量a 在向量b 方向上的投影，则m 的最大值是A.2 B. 4C. D. 37、函数sin()(0)2y x πϕϕ=+>的部分图象如图所示,设P 是图象的最高点,,A B 是图象与x 轴的交点,则tan APB ∠_________.已知三角形的一边长为4,所对角为60°,则另两边长之积的最大值等于______.8．在ΔABC中，22sin 2A A =，sin()2cos sin B C B C -=，则AC AB__________。

9.已知524cos ,53sin +-=+-=m mx m m x ，且3,22x ππ⎛⎫∈ ⎪⎝⎭，则=x tan10.已知函数()cos sin f x x x =，给出下列四个结论： ①若12()()f x f x =-，则12x x =-；②()f x 的最小正周期是2π；③()f x 在区间[,]44ππ-上是增函数；④()f x 的图象关于直线34x π=对称．其中正确的结论是 . 11、设x x x x f cos sin 32cos 6)(2-=.(Ⅰ)求)(x f 的最小正周期及单调递增区间;(Ⅱ)将函数)(x f 的图象向右平移3π个单位,得)(x g y =的图象,求x x g x F 323)()(-=在4π=x 处的切线方程.12．如图，A 是单位圆与x 轴正半轴的交点，点B 、P 在单位圆上，且34(,)55B -，,(0)AOB AOP αθθπ∠=∠=<<，OQ OA OP =+ ，四边形OAQP 的面积为S. Ⅰ）求cos sin αα+；Ⅱ）求OA OQ S ⋅+的最大值及此时θ的值θ0.13. 已知函数()s i n 2()4s i n ()s i n (23433f x x x x πππ=+++-．(I)求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域；(Ⅱ)若对于任意的x R ∈，不等式0()()f x f x ≤恒成立，求0sin(2)3x π-． 14. 已知向量(sin ,1)m x =-，向量1,)2n x = ，函数()()f x m n =+ ·m 。

投影与视图一、选择题1. （2014•四川巴中，第5题3分）如图，两个大小不同的实心球在水平面靠在一起组成如图所示的几何体，则该几何体的左视图是（）A．两个外切的圆B．两个内切的圆C．两个内含的圆D．一个圆考点：三视图．分析：根据左视图是从左面看得到的视图，圆的位置关系解答即可．解答：从左面看，为两个内切的圆，切点在水平面上，所以，该几何体的左视图是两个内切的圆．故选B．点评：本题考查了三视图的知识，左视图是从物体的左面看得到的视图．2. （2014•山东威海，第6题3分）用四个相同的小立方体搭几何体，要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的，下列四种摆放方式中不符合要求、此几何体的主视图和俯视图都是“、此几何体的主视图和左视图都是、此几何体的主视图和左视图都是、此几何体的主视图是，俯视图是3. （2014•山东潍坊，第4题3分）一个几何体的三视图如右图所示，则该几何体是( )考点：由三视图还原实物图．分析：根据主视图、左视图、俯视图的形状，将它们相交得到几何体的形状．解答：由三视图知，从正面和侧面看都是上面梯形，下面长方形，从上面看为圆环，可以想象到实物体上面是圆台，下面是空心圆柱．故选D．点评：本题考查几何体的三视图与直观图之间的相互转化．4.（2014•山东烟台，第4题3分）如图是一个正方体截去一角后得到的几何体，它的主视图是（）A．B．C．D．考点：三视图．分析：根据主视图是从正面看到的图形判定则可．解答：从正面看，主视图为．故选：C．点评：本题考查了三视图的知识，根据主视图是从物体的正面看得到的视图得出是解题关键．BD6．（2014•湖南张家界，第5题，3分）某几何体的主视图、左视图和俯视图分别如图，则该几何体的体积为（）视方向，则它的主视图可以是解析：选B. ∵上下两凸起是圆弧，非圆，中间是两个圆片的叠合,其主视图应为矩形. 8．（2014山东济南，第6题，3分）如图，一个几何体由5个大小相同、棱长为1的正方体搭成，下列关于这个几何体的说法正确的是第6题A．主视图的面积为5 B．左视图的面积为3C．俯视图的面积为3 D．三种视图的面积都是4【解析】主题图、俯视图均为4个正方形，其面积为4，左视图为3个正方形，其面积为3，故选B．9．（2014•山东聊城，第2题，3分）如图是一个三棱柱的立体图形，它的主视图是（）B D10．（2014•浙江杭州，第2题，3分）已知一个圆锥体的三视图如图所示，则这个圆锥的侧面积为（）该礼盒的主视图是（ ）A ．B ．C ．D ．考点： 简单组合体的三视图．分析： 找到从正面看所得到的图形即可．解答： 解：从正面看，是两个矩形，右边的较小． 故选A ．点评： 本题考查了三视图的知识，主视图是从物体的正面看得到的视图． 13:将两个长方体如图放置，到所构成的几何体的左视图可能是（ ）答案：C解析：根据三视图可知，C正确。

锐角三角函数与特殊角
一、填空题
1．（2014•广西来宾，第17题3分）如图，Rt△ABC中，∠C=90°，∠B=30°，BC=6，则AB的长为．
2．(2014年贵州安顺，第9题3分)如图，在Rt△ABC中，∠C=90°，∠A=30°，E为AB上一点且AE：EB=4：1，EF⊥AC于F，连接FB，则tan∠CFB的值等于（）
A B．C．D．
二、填空题
1．(2014年广西南宁，第17题3分）如图，一渔船由西往东航行，在A点测得海岛C位于北偏东40°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD等于10
海里．
2．（2014•攀枝花，第14题4分）在△ABC中，如果∠A、∠B满足|tanA﹣1|+（cosB﹣）2=0，那么∠C= ．
三、解答题
2．（2014•贵州黔西南州, 第21题6分）（1）计算：（）﹣2+（π﹣2014）0+sin60°+|﹣2|．
3．（2014•四川成都,第15题6分）（1）计算：﹣4sin30°+（2014﹣π）0﹣22．
1．(2014年广西钦州，第24题9分)如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED=60°，在离电线杆6米的B处安置高为1.5米的测角仪AB，在A处测得电线杆上C处的仰角为30°，求拉线CE的长（结果保留小数点后一位，参考数据：≈1.41，≈1.73）．。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

专题检测卷(十四)空间几何体的三视图、表面积及体积(40分钟)一、选择题1.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )2.(2013·新课标全国卷Ⅰ)某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π3.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的表面积为( )A.πB.πC.πD.π4.(2013·大同模拟)如图1,边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B三点重合于G,所得三棱锥G-DEF的俯视图如图2,则该三棱锥正视图的面积为( )A. B.C. D.5.(2013·肇庆模拟)已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中最大的面积是( )A.3B.2C.6D.8二、填空题6.(2013·北京模拟)某四棱锥的三视图如图所示,该四棱锥的体积是.7.(2013·江苏高考)如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2= .8.一个几何体的三视图如图所示,则这个几何体的体积是.三、解答题9.(2013·珠海模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.(1)请画出该几何体的直观图,并求出它的体积.(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD-A1B1C1D1?如何组拼?试证明你的结论.10.已知四面体ABCD(图1),将其沿AB,AC,AD剪开,展成的平面图形正好是图2所示的直角梯形A1A2A3D(梯形的顶点A1,A2,A3重合于四面体的顶点A).(1)证明:AB⊥CD.(2)当A1D=10,A1A2=8时,求四面体ABCD的体积.11.(2013·中山模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,D,E分别为A1B1,AA1的中点,点F在棱AB上,且AF=AB.(1)求证:EF∥平面BDC1.(2)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1∶15,若存在,指出点G的位置;若不存在,说明理由.答案解析1.【解析】选D.抓住其一条对角线被遮住应为虚线,可知正确答案在C,D中,又结合直观图知,D正确.2.【解题提示】观察三视图,根据三视图确定几何体的构成,利用圆柱及长方体的体积公式求解.【解析】选A.由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为×π×22×4+2×2×4=16+8π.3.【解析】选B.由题意知,外接球球心在侧视图的高上,设为O,半径为r,则r2=(-r)2+1,解得r=,从而S=4πr2=.4.【解析】选B.设正视图的高为h,V G-DEF=V D-GEF=××××h=××1×1×2,得h=,所以正视图S=××=.5.【解析】选C.四棱锥的直观图如图所示,PN=,PM=3,S△PDC=×4×=2, S△PBC=S△PAD=×2×3=3,S△PAB=×4×3=6.6.【解析】由三视图可知,四棱锥的高为2,底面为直角梯形ABCD.其中DC=2,AB=3,BC=,所以四棱锥的体积为××2=.答案:【误区警示】解答本题时易因不能确定四棱锥的底面边长而无法求解.7.【解析】设三棱柱的底面ABC的面积为S,三棱柱的高为h,则其体积为V2=Sh.因为D,E分别为AB,AC的中点,所以△ADE的面积等于S,又因为F为AA1的中点,所以三棱锥F-ADE的高等于h,于是三棱锥F-ADE的体积V1=×S〃h=Sh=V2,故V1∶V2=1∶24.答案:1∶248.【解析】该几何体是一个四棱锥,如图.体积V=Sh=S梯形ABCD〃BP=××2=4.答案:49.【解析】(1)该几何体的直观图如图1所示,它是有一条侧棱垂直于底面的四棱锥.其中底面ABCD是边长为6的正方形,高为CC1=6,故所求体积是V=×62×6=72.(2)依题意,正方体的体积是原四棱锥体积的3倍,故用3个这样的四棱锥可以拼成一个棱长为6的正方体,其拼法如图2所示.证明:因为面ABCD、面ABB1A1、面AA1D1D为全等的正方形,所以==,故所拼图形成立.10.【解析】(1)在四面体ABCD中,⇒AB⊥平面ACD⇒AB⊥CD.(2)在题图2中作DE⊥A2A3于E.因为A1A2=8,所以DE=8.又因为A1D=A3D=10,所以EA3=6,A2A3=10+6=16.又A2C=A3C,所以A3C=8,即题图1中AC=8,AD=10,由A1A2=8,A1B=A2B得题图1中AB=4,所以S △ACD==DE〃A3C=×8×8=32.又因为AB⊥平面ACD,所以V B-ACD=×32×4=.11.【解析】(1)取AB的中点M,连结A1M,因为AF=AB,所以F为AM的中点,又因为E为AA1的中点,所以EF∥A1M.在三棱柱ABC-A1B1C1中,D,M分别为A1B1,AB的中点,所以A1D∥BM,A1D=BM,所以四边形A1DBM为平行四边形,所以A1M∥BD,所以EF∥BD.因为BD 平面BDC1,EF⊄平面BDC1,所以EF∥平面BDC1.(2)设AC上存在一点G,使得平面EFG将三棱柱分割成的两部分体积之比为1∶15,则V E-AFG∶=1∶16,因为==×××=〃,所以〃=,所以=,所以AG=AC>AC.所以符合要求的点G不存在.关闭Word文档返回原板块。

课时 40．视图与投影【课前热身】1.以以以下图的物体是一个几何体，其主视图是（）A. B. C. D.2.如图，圆柱的左视图是（）A.Ｂ．Ｃ．Ｄ．3.在一个光亮的上午，小丽拿着一块矩形木板在阳光下做投影实验，矩形木板在地面上形成的投影不能够能是（）．．．A. B. C. D.4. 如图是每个面上都有一个汉字的正方体讲的一种张开图，那么在正方体的表面，与“迎”相文明迎奥对的面上的汉字是（）运A.文B.明C.奥D.运5.右图是某一几何体的三视图，则这个几何体是（）A．圆柱体B．圆锥体C．正方体D．球体【考点链接】1.从观察物体时，看到的图叫做主视图；从观察物体时，看到的图叫做左视图；从观察物体时，看到的图叫做俯视图.2.主视图与俯视图的一致；主视图与左视图的一致；俯视图与左视图的一致 .3.叫盲区 .4.投影可分为平行投影与中心投影. 此中所形成的投影叫平行投影；所形成的投影叫中心投影 .5.利用光辉能否平行或能否交于一点来判断是投影或投影，以及光源的地点和物体暗影的地点 .【典例精析】例 1如图 4，是一个由若干个相同的小正方体构成的几何体的三视图，则构成这个几何体的小正方体的个数是（）1A．7个B．8个C．9个D．10个例 2 （ 1）一木杆按如图 1 所示的方式直立在地面上，请在图中画出它在阳光下的影子（用线段 CD 表示）；（ 2）图 2 是两根标杆及它们在灯光下的影子．请在图中画出光源的地点（用点示），并在图中画出人在此光源下的影子．（用线段 EF 表示）．P 表太阳光辉B 木杆AB A图 1图 2【中考演练】1.当物体的某个面平行于投影面时，这个面的正投影与这个面的形状、大小．（填“相同”、“不用然相同” 、“不一样样”之一）．2. 如图，水平搁置的长方体的底面是边长为 2 和 4 的矩形，它的左视图的面积为6，则长方体的体积等于．23. 以以下图的几何体是由三个相同大小的立方体搭4成的，其左视图为（）A．B．C．D．4.在学校张开的“为灾区小孩过六一” 的活动中，晶晶把自己最喜欢的铅笔盒送给灾区儿童．这个铅笔盒（右图）的左视图是（）5.将图所示的Rt△ ABC A．绕直角边B．C．D．AB 旋转一周，所得几何体的主视图为（）AC BA．B．C．D．26.若干桶方便面摆放在桌子上，以以以下图是它的三视图，则这一堆方便面共有（）主视图左视图俯视图A．6 桶B．7桶C．8 桶D．9 桶7.六个大小相同的正方体搭成的几何体以以以下图，则关于它的视图说法正确的选项是（A．正视图的面积最大B．左视图的面积最大C．俯视图的面积最大D．三个视图的面积相同大8.若一个几何体的主视图、左视图、俯视图分别是三角形、三角形、圆，则这个几何体可能是（）A．球B．圆柱 C ．圆锥 D ．棱锥9.以下四个几何体中，主视图、左视图、俯视图完满相同的是（）A．圆锥 B ．球C．圆柱D．三棱柱3。

【母题来源一】【2019•天津】2sin60°的值等于 A ．1BCD ．2【答案】C 【解析】2sin60°=2=，故选C ． 【名师点睛】本题考查了特殊角三角函数值，解决此类题目的关键是熟记特殊角的三角函数值． 【母题来源二】【2019•宜昌】如图，在5×4的正方形网格中，每个小正方形的边长都是1，△ABC 的顶点都在这些小正方形的顶点上，则sin ∠BAC 的值为A ．43B ．34C ．35D ．45【答案】D【解析】如图，过C 作CD ⊥AB 于D ，则∠ADC =90°， ∴AC ===5．专题13 锐角三角函数、视图与投影∴sin ∠BAC 45CD AC ==． 故选D ．【名师点睛】本题考查了勾股定理的运用以及锐角三角函数，正确作出辅助线是解题的关键．【母题来源三】【2019•甘肃】在△ABC 中，∠C =90°，tan A 3=，则cos B =__________． 【答案】12【解析】∵tan A 3=A =30°， ∵∠C =90°，∴∠B =60°，∴cos B =cos60°12=．故答案为：12．【名师点睛】此题考查的知识点是锐角三角函数的定义：在直角三角形中，一个锐角的余弦等于这个角的邻边与斜边的比值，一个锐角的正切等于这个角的对边与邻边的比值；也可利用特殊角的三角函数值求解．【母题来源四】【2019•柳州】如图，在△ABC 中，sin B 13=，tan C 2=，AB =3，则AC 的长为__________．【解析】如图，过A 作AD ⊥BC ，在Rt △ABD 中，sin B 13=，AB =3， ∴AD =AB ·sin B =1，在Rt △ACD 中，tan C 2=，∴2AD CD =，即CD =根据勾股定理得：AC ==．【名师点睛】此题考查了解直角三角形，涉及的知识有：锐角三角函数定义，以及勾股定理，熟练掌握各自的性质是解本题的关键．【母题来源五】【2019•贺州】如图，在A 处的正东方向有一港口B ．某巡逻艇从A 处沿着北偏东60°方向巡逻，到达C 处时接到命令，立刻在C 处沿东南方向以20海里/小时的速度行驶3小时到达港口B ．求A ，B ≈1.73≈1.4，结果保留一位小数）．【解析】过点C 作CD ⊥AB ，垂足为点D ，则∠ACD =60°，∠BCD =45°，如图所示．在Rt △BCD 中，sin ∠BCD BD BC =，cos ∠BCD CDBC=，∴BD =BC ·sin ∠BCD =20×32⨯≈42，CD =BC ·cos ∠BCD =20×32⨯≈42； 在Rt △ACD 中，tan ∠ACD AD CD=，∴AD =CD ·tan ∠ACD =42≈72.7． ∴AB =AD +BD =72.7+42=114.7． ∴A ，B 间的距离约为114.7海里．【名师点睛】本题考查了解直角三角形的应用-方向角问题，通过解直角三角形，求出BD ，AD 的长是解题的关键．【母题来源六】【2019•河南】数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE 在高55 m 的小山EC 上，在A 处测得塑像底部E 的仰角为34°，再沿AC 方向前进21 m 到达B 处，测得塑像顶部D 的仰角为60°，求炎帝塑像DE 的高度．（精确到1 m ．参考数据：sin34°≈0.56，cos34°=0.83，tan34°≈0.67≈1.73）【解析】∵∠ACE =90°，∠CAE =34°，CE =55 m ，∴tan ∠CAE CEAC =， ∴AC 55tan 340.67CE ==≈︒82.1 m ， ∵AB =21 m ，∴BC =AC -AB =61.1 m ，在Rt △BCD 中，tan60°CDBC==∴CD =≈1.73×61.1≈105.7 m ， ∴DE =CD -EC =105.7-55≈51 m ， 答：炎帝塑像DE 的高度约为51 m ．【名师点睛】本题考查了解直角三角形的应用，解答本题的关键是根据仰角和俯角构造直角三角形，利用三角函数的知识求解，难度适中．【母题来源七】【2019•眉山】如图，在岷江的右岸边有一高楼AB ，左岸边有一坡度i =1∶2的山坡CF ，点C 与点B 在同一水平面上，CF 与AB 在同一平面内．某数学兴趣小组为了测量楼AB 的高度，在坡底C处测得楼顶A 的仰角为45°，然后沿坡面CF 上行了D 处，此时在D 处测得楼顶A 的仰角为30°，求楼AB 的高度．【解析】在Rt △DEC 中，∵i 12DE EC ==，DE 2+EC 2=CD 2，CD∴DE 2+（2DE ）2=（2， 解得：DE =20（m ）， ∴EC =40 m ，过点D 作DG ⊥AB 于G ，过点C 作CH ⊥DG 于H ，如图所示：则四边形DEBG 、四边形DECH 、四边形BCHG 都是矩形， ∵∠ACB =45°，AB ⊥BC ， ∴AB =BC ， 设AB =BC =x m ，则AG =（x -20）m ，DG =（x +40）m ， 在Rt △ADG 中，∵AGDG=tan ∠ADG ，∴2040x x -=+，解得：x答：楼AB 的高度为（）米．【名师点睛】本题考查了解直角三角形的应用-方向角问题，通过解直角三角形得出方程是解题的关键． 【母题来源八】【2019•江西】图1是一台实物投影仪，图2是它的示意图，折线B -A -O 表示固定支架，AO垂直水平桌面OE于点O，点B为旋转点，BC可转动，当BC绕点B顺时针旋转时，投影探头CD始终垂直于水平桌面OE，经测量：AO=6.8 cm，CD=8 cm，AB=30 cm，BC=35 cm．（结果精确到0.1）．（1）如图2，∠ABC=70°，BC∥OE．①填空：∠BAO=__________．②求投影探头的端点D到桌面OE的距离．（2）如图3，将（1）中的BC向下旋转，当投影探头的端点D到桌面OE的距离为6 cm时，求∠ABC 的大小．（参考数据：sin70°≈0.94，cos20°≈0.94，sin36.8°≈0.60，cos53.2°≈0.60）【解析】（1）①过点A作AG∥BC，如图1，则∠BAG=∠ABC=70°，∵BC∥OE，∴AG∥OE，∴∠GAO=∠AOE=90°，∴∠BAO=90°+70°=160°，故答案为：160．②过点A作AF⊥BC于点F，如图2，则AF=AB·sin∠ABE=30sin70°≈28.2（cm），∴投影探头的端点D到桌面OE的距离为：AF+0A-CD=28.2+6.8-8=27（cm）．（2）过点DE⊥OE于点H，过点B作BM⊥CD，与DC延长线相交于点M，过A作AF⊥BM于点F，如图3，则∠MBA=70°，AF=28.2 cm，DH=6 cm，BC=30 cm，CD=8 cm，∴CM=AF+AO-DH-CD=28.2+6.8-6-8=21（cm），∴sin∠MBC210.635CMBC===，∴∠MBC=36.8°，∴∠ABC=∠ABM-∠MBC=33.2°．【名师点睛】此题主要考查了解直角三角形的应用，充分体现了数学与实际生活的密切联系，解题的关键是构造直角三角形．【命题意图】这类试题主要考查特殊角的三角函数、解直角三角形、解直角三角形的实际应用等．【方法总结】1．解直角三角形的常用关系：在Rt△ABC中，∠C=90°，则：（1）三边关系：a2+b2=c2；（2）两锐角关系：∠A+∠B=90°；（3）边与角关系：sin A=cos B=ac，cos A=sin B=bc，tan A=ab；（4）sin2A+cos2A=1．2．解直角三角形的应用可解决的问题（1）测量物体的高度；（2）测量河的宽度；（3）解决航海航空问题；（4）解决坡度问题；（5）解决实际生活中其他问题.【母题来源九】【2019•黄冈】如图，是由棱长都相等的四个小正方体组成的几何体．该几何体的左视图是A．B．C．D．【答案】B【解析】该几何体的左视图只有一列，含有两个正方形．故选B．【名师点睛】此题主要考查了简单组合体的三视图，关键是掌握左视图所看的位置．【母题来源十】【2019•河南】如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②．关于平移前后几何体的三视图，下列说法正确的是A．主视图相同B．左视图相同C．俯视图相同D．三种视图都不相同【答案】C【解析】图①的三视图为：图②的三视图为：，故选C．【名师点睛】本题考查了由三视图判断几何体，解题的关键是学生的观察能力和对几何体三种视图的空间想象能力．【母题来源十一】【2019•福建】如图是由一个长方体和一个球组成的几何体，它的主视图是A．B．C．D．【答案】C【解析】几何体的主视图为：，故选C．【名师点睛】此题考查了简单组合体的三视图，主视图即为从正面看几何体得到的视图．【母题来源十二】【2019•安徽】一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是A．B．C．D．【答案】C【解析】几何体的俯视图是：，故选C．【名师点睛】本题考查了三视图的知识，俯视图是从物体的正面看得到的视图．【母题来源十三】【2019•长沙】某个几何体的三视图如图所示，该几何体是A．B．C．D．【答案】D【解析】由三视图可知：该几何体为圆锥．故选D．【名师点睛】考查了由三视图判断几何体的知识，解题的关键是具有较强的空间想象能力，难度不大．【母题来源十四】【2019•深圳】下列哪个图形是正方体的展开图A．B．C．D．【答案】B【解析】根据正方体展开图的特征，选项A、C、D不是正方体展开图；选项B是正方体展开图．故选B．【名师点睛】此题主要考查了正方体的展开图，正方体展开图有11种特征，分四种类型，即：第一种：“1﹣4﹣1”结构，即第一行放1个，第二行放4个，第三行放1个；第二种：“2﹣2﹣2”结构，即每一行放2个正方形，此种结构只有一种展开图；第三种：“3﹣3”结构，即每一行放3个正方形，只有一种展开图；第四种：“1﹣3﹣2”结构，即第一行放1个正方形，第二行放3个正方形，第三行放2个正方形．【命题意图】这类试题主要考查三视图、正方体的展开图．【方法总结】1．（1）画三视图要注意三要素：主视图与俯视图长度相等；主视图与左视图高度相等；左视图与俯视图宽度相等．简记为“主俯长对正，主左高平齐，左俯宽相等”．（2）注意实线与虚线的区别：能看到的线用实线，看不到的线用虚线．2．正方体展开图口诀：正方体展有规律，十一种类看仔细；中间四个成一行，两边各一无规矩；二三紧连错一个，三一相连一随意；两两相连各错一，三个两排一对齐；一条线上不过四，田七和凹要放弃；相间之端是对面，间二拐角面相邻．1．【2019年江苏省盐城市东台市中考数学模拟试卷（5月份）】如图，由5个完全相同的小正方体组合成的几何体，它的俯视图为A ．B ．C ．D ．2．【黑龙江省哈尔滨市南岗区2019届九年级中考一模数学试题】下列图形中，主视图为矩形的是 A ． B ． C ． D ．3．【2019年浙江省金华市东阳市吴宁镇中考数学模拟试卷（5月份）】如图所示零件的左视图是A ．B ．C ．D ．4．【2019年河南省新乡市卫辉市中考数学一模试卷】如图所示是正方形的展开图，原正方体相对两个面上的数字之和的最大值是A ．5B ．6C ．7D ．85．【天津市滨海新区2019届中考一模数学试题】cos45 的值等于A B C ．12 D ．26．【黑龙江省哈尔滨市南岗区2019届九年级中考一模数学试题】如图，航拍无人机从A 处测得一幢建筑物顶部B 的仰角为45°，侧得底部C 的俯角为60°，此时航拍无人机与该建筑物的水平距离AD 为90米，那么该建筑物的高度BC 为A ．B ．C ．D ．7．【2019年广东省深圳市罗湖区中考数学二模试卷】如图，小山岗的斜坡AC 的坡度是tan α=34，在与山脚C 距离200米的D 处，测得山顶A 的仰角为26.6°，则小山岗的高AB 是（结果取整数，参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）A ．300米B ．250米C ．400米D ．100米8．【山东省郓城县初中数学中考考试模拟试题】如图，在边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则tan ∠ABC 的值为A ．35B ．34CD ．19．【2019年湖北省孝感市安陆市、应城市、云梦县、孝昌县四县市中考数学三模试卷】如图，在△ABC 中，∠B =45°，tan C =12，AB ，则AC =__________．10．【2019年河北省保定市中考数学一模试卷】如图，斜面AC 的坡度（CD 与AD 的比）为1∶2，AC 米，坡顶有旗杆BC ，旗杆顶端B 点与A 点有一条彩带相连．若AB =13米，则旗杆BC 的高度为__________米．11．【2019年山东省淄博市桓台区中考数学二模试卷】如图，某风景区内有一瀑布，AB表示瀑布的垂直高度，在与瀑布底端同一水平位置的点D处测得瀑布顶端A的仰角β为45°，沿坡度i=1∶3的斜坡向上走100米，到达观景台C，在C处测得瀑布顶端A的仰角α为37°，若点B、D、E在同一水平线上．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75≈1.41≈3.16）（1）观景台的高度CE为__________米（结果保留准确值）；（2）求瀑布的落差AB（结果保留整数）．12．【2019年浙江省宁波市北仑区中考数学模拟试卷】如图1，是小明荡秋千的侧面示意图，秋千链长AB=5 m（秋千踏板视作一个点），静止时秋千位于铅垂线BC上，此时秋千踏板A到地面的距离为0.5 m．（1）当摆角为37°时，求秋千踏板A与地面的距离AH；（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）（2）如图2，当秋千踏板摆动到点D时，点D到BC的距离DE=4 m；当他从D处摆动到D'处时，恰好D'B⊥DB，求点D'到BC的距离．。

一、锐角三角函数真题与模拟题分类汇编（难题易错题）1．某地是国家AAAA 级旅游景区，以“奇山奇水奇石景，古賨古洞古部落”享誉巴渠，被誉为 “小九寨”．端坐在观音崖旁的一块奇石似一只“啸天犬”，昂首向天，望穿古今．一个周末，某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离．他们把蹲着的“啸天犬”抽象成四边形ABCD ，想法测出了尾部C 看头顶B 的仰角为40，从前脚落地点D 看上嘴尖A 的仰角刚好60，5CB m ＝, 2.7CD m ＝．景区管理员告诉同学们，上嘴尖到地面的距离是3m ．于是，他们很快就算出了AB 的长．你也算算？（结果精确到0.1m ．参考数据：400.64400.77400.84sin cos tan ︒≈︒≈︒≈，，.2 1.41,3 1.73≈≈）【答案】AB 的长约为0.6m ． 【解析】 【分析】作BF CE ⊥于F ，根据正弦的定义求出BF ，利用余弦的定义求出CF ，利用正切的定义求出DE ，结合图形计算即可． 【详解】解：作BF CE ⊥于F ，在Rt BFC ∆中， 3.20BF BC sin BCF ⋅∠≈＝，3.85CF BC cos BCF ⋅∠≈＝，在Rt ADE ∆E 中，3 1.73tan 3AB DE ADE ===≈∠， 0.200.58BH BF HF AH EF CD DE CF ∴+＝﹣＝，＝＝﹣＝由勾股定理得，22BH AH 0.6(m)AB =+≈， 答：AB 的长约为0.6m ．【点睛】考查的是解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．2．在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE=12∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．（1）当点P与点C重合时（如图1）．求证：△BOG≌△POE；（2）通过观察、测量、猜想：BFPE=，并结合图2证明你的猜想；（3）把正方形ABCD改为菱形，其他条件不变（如图3），若∠ACB=α，求BF PE的值．（用含α的式子表示）【答案】（1）证明见解析（2）12BFPE=（3）1tan2BFPEα=【解析】解：（1）证明：∵四边形ABCD是正方形，P与C重合，∴OB="OP" ，∠BOC=∠BOG=90°．∵PF⊥BG ，∠PFB=90°，∴∠GBO=90°—∠BGO，∠EPO=90°—∠BGO．∴∠GBO=∠EPO ．∴△BOG≌△POE（AAS）．（2）BF1PE2=．证明如下：如图，过P作PM//AC交BG于M，交BO于N，∴∠PNE=∠BOC=900，∠BPN=∠OCB．∵∠OBC=∠OCB =450，∴∠NBP=∠NPB．∴NB=NP．∵∠MBN=900—∠BMN ， ∠NPE=900—∠BMN ，∴∠MBN=∠NPE ． ∴△BMN ≌△PEN （ASA ）．∴BM=PE ．∵∠BPE=12∠ACB ，∠BPN=∠ACB ，∴∠BPF=∠MPF ． ∵PF ⊥BM ，∴∠BFP=∠MFP=900．又∵PF=PF ， ∴△BPF ≌△MPF （ASA ）．∴BF="MF" ，即BF=12BM ． ∴BF=12PE ， 即BF 1PE 2=． （3）如图，过P 作PM//AC 交BG 于点M ，交BO 于点N ，∴∠BPN=∠ACB=α，∠PNE=∠BOC=900．由（2）同理可得BF=12BM ， ∠MBN=∠EPN ． ∵∠BNM=∠PNE=900，∴△BMN ∽△PEN ．∴BM BNPE PN=． 在Rt △BNP 中，BN tan =PN α， ∴BM =tan PE α，即2BF=tan PEα． ∴BF 1=tan PE 2α． （1）由正方形的性质可由AAS 证得△BOG ≌△POE ．（2）过P 作PM//AC 交BG 于M ，交BO 于N ，通过ASA 证明△BMN ≌△PEN 得到BM=PE ，通过ASA 证明△BPF ≌△MPF 得到BF=MF ，即可得出BF 1PE 2=的结论． （3）过P 作PM//AC 交BG 于点M ，交BO 于点N ，同（2）证得BF=12BM ， ∠MBN=∠EPN ，从而可证得△BMN ∽△PEN ，由BM BN PE PN =和Rt △BNP 中BNtan =PNα即可求得BF 1=tan PE 2α．3．已知Rt △ABC 中，AB 是⊙O 的弦，斜边AC 交⊙O 于点D ，且AD=DC ，延长CB 交⊙O 于点E ．（1）图1的A、B、C、D、E五个点中，是否存在某两点间的距离等于线段CE的长？请说明理由；（2）如图2，过点E作⊙O的切线，交AC的延长线于点F．①若CF=CD时，求sin∠CAB的值；②若CF=aCD（a＞0）时，试猜想sin∠CAB的值．（用含a的代数式表示，直接写出结果）【答案】（1）AE=CE；（2）①；②．【解析】试题分析：（1）连接AE、DE，如图1，根据圆周角定理可得∠ADE=∠ABE=90°，由于AD=DC，根据垂直平分线的性质可得AE=CE；（2）连接AE、ED，如图2，由∠ABE=90°可得AE是⊙O的直径，根据切线的性质可得∠AEF=90°，从而可证到△ADE∽△AEF，然后运用相似三角形的性质可得=AD•AF．①当CF=CD时，可得，从而有EC=AE=CD，在Rt△DEC中运用三角函数可得sin∠CED=，根据圆周角定理可得∠CAB=∠DEC，即可求出sin∠CAB的值；②当CF=aCD（a＞0）时，同①即可解决问题．试题解析：（1）AE=CE．理由：连接AE、DE，如图1，∵∠ABC=90°，∴∠ABE=90，∴∠ADE=∠ABE=90°，∵AD=DC，∴AE=CE；（2）连接AE、ED，如图2，∵∠ABE=90°，∴AE是⊙O的直径，∵EF是⊙OO的切线，∴∠AEF=90°，∴∠ADE=∠AEF=90°，又∵∠DAE=∠EAF，∴△ADE∽△AEF，∴，∴=AD•AF．①当CF=CD时，AD=DC=CF，AF=3DC，∴=DC•3DC=，∴AE=DC，∵EC=AE，∴EC=DC，∴sin∠CAB=sin∠CED===；②当CF=aCD（a＞0）时，sin∠CAB=．∵CF=aCD，AD=DC，∴AF=AD+DC+CF=（a+2）CD，∴=DC•（a+2）DC=（a+2），∴AE=DC，∵EC=AE，∴EC=DC，∴sin∠CAB=sin∠CED==．考点：1．圆的综合题；2．探究型；3．存在型．4．如图，抛物线C1：y=（x+m）2（m为常数，m＞0），平移抛物线y=﹣x2，使其顶点D 在抛物线C1位于y轴右侧的图象上，得到抛物线C2．抛物线C2交x轴于A，B两点（点A 在点B的左侧），交y轴于点C，设点D的横坐标为a．（1）如图1，若m=．①当OC=2时，求抛物线C2的解析式；②是否存在a，使得线段BC上有一点P，满足点B与点C到直线OP的距离之和最大且AP=BP？若存在，求出a的值；若不存在，请说明理由；（2）如图2，当OB=2﹣m（0＜m＜）时，请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标（用含m的式子表示）．【答案】(1) ①y=﹣x2+x+2．②．（2）P1（﹣m，1），P2（﹣m，﹣3），P3（﹣﹣m，3），P4（3﹣m，3）．【解析】试题分析：（1）①首先写出平移后抛物线C2的解析式（含有未知数a），然后利用点C （0，2）在C2上，求出抛物线C2的解析式；②认真审题，题中条件“AP=BP”意味着点P在对称轴上，“点B与点C到直线OP的距离之和最大”意味着OP⊥BC．画出图形，如图1所示，利用三角函数（或相似），求出a的值；（2）解题要点有3个：i）判定△ABD为等边三角形；ii）理论依据是角平分线的性质，即角平分线上的点到角两边的距离相等；iii）满足条件的点有4个，即△ABD形内1个（内心），形外3个．不要漏解．试题解析：（1）当m=时，抛物线C1：y=（x+）2．∵抛物线C2的顶点D在抛物线C1上，且横坐标为a，∴D（a，（a+）2）．∴抛物线C2：y=﹣（x﹣a）2+（a+）2（I）．①∵OC=2，∴C（0，2）．∵点C在抛物线C2上，∴﹣（0﹣a）2+（a+）2=2，解得：a=，代入（I）式，得抛物线C2的解析式为：y=﹣x2+x+2．②在（I）式中，令y=0，即：﹣（x﹣a）2+（a+）2=0，解得x=2a+或x=﹣，∴B（2a+，0）；令x=0，得：y=a+，∴C（0，a+）．设直线BC的解析式为y=kx+b，则有：，解得，∴直线BC的解析式为：y=﹣x+（a+）．假设存在满足条件的a值．∵AP=BP，∴点P在AB的垂直平分线上，即点P在C2的对称轴上；∵点B与点C到直线OP的距离之和≤BC，只有OP⊥BC时等号成立，∴OP⊥BC．如图1所示，设C2对称轴x=a（a＞0）与BC交于点P，与x轴交于点E，则OP⊥BC，OE=a．∵点P在直线BC上，∴P（a，a+），PE=a+．∵tan∠EOP=tan∠BCO=，∴，解得：a=．∴存在a=，使得线段BC上有一点P，满足点B与点C到直线OP的距离之和最大且AP="BP"（3）∵抛物线C2的顶点D在抛物线C1上，且横坐标为a，∴D（a，（a+m）2）．∴抛物线C2：y=﹣（x﹣a）2+（a+m）2．令y=0，即﹣（x﹣a）2+（a+m）2=0，解得：x1=2a+m，x2=﹣m，∴B（2a+m，0）．∵OB=2﹣m，∴2a+m=2﹣m，∴a=﹣m．∴D（﹣m，3）．AB=OB+OA=2﹣m+m=2．如图2所示，设对称轴与x轴交于点E，则DE=3，BE=AB=，OE=OB﹣BE=﹣m．∵tan∠ABD=，∴∠ABD=60°．又∵AD=BD，∴△ABD为等边三角形．作∠ABD的平分线，交DE于点P1，则P1E=BE•tan30°=×=1，∴P1（﹣m，1）；在△ABD形外，依次作各个外角的平分线，它们相交于点P2、P3、P4．在Rt△BEP2中，P2E=BE•tan60°=•=3，∴P2（﹣m，﹣3）；易知△ADP3、△BDP4均为等边三角形，∴DP3=DP4=AB=2，且P3P4∥x轴．∴P3（﹣﹣m，3）、P4（3﹣m，3）．综上所述，到△ABD的三边所在直线的距离相等的所有点有4个，其坐标为：P1（﹣m，1），P2（﹣m，﹣3），P3（﹣﹣m，3），P4（3﹣m，3）．【考点】二次函数综合题．5．如图（1），已知正方形ABCD在直线MN的上方BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．（1）连接GD，求证：△ADG≌△ABE；（2）连接FC，观察并直接写出∠FCN的度数（不要写出解答过程）（3）如图（2），将图中正方形ABCD改为矩形ABCD，AB＝6，BC＝8，E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请求出tan∠FCN的值．若∠FCN的大小发生改变，请举例说明．【答案】（1）见解析；（2）∠FCN ＝45°，理由见解析；（3）当点E 由B 向C 运动时，∠FCN 的大小总保持不变，tan ∠FCN ＝43．理由见解析. 【解析】 【分析】（1）根据三角形判定方法进行证明即可．（2）作FH ⊥MN 于H ．先证△ABE ≌△EHF ，得到对应边相等，从而推出△CHF 是等腰直角三角形，∠FCH 的度数就可以求得了．（3）解法同（2），结合（1）（2）得：△EFH ≌△GAD ，△EFH ∽△ABE ，得出EH=AD=BC=8，由三角函数定义即可得出结论． 【详解】（1）证明：∵四边形ABCD 和四边形AEFG 是正方形， ∴AB ＝AD ，AE ＝AG ＝EF ，∠BAD ＝∠EAG ＝∠ADC ＝90°， ∴∠BAE +∠EAD ＝∠DAG +∠EAD ，∠ADG ＝90°＝∠ABE ， ∴∠BAE ＝∠DAG ， 在△ADG 和△ABE 中，ADG ABE DAG BAE AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ADG ≌△ABE （AAS ）． （2）解：∠FCN ＝45°，理由如下： 作FH ⊥MN 于H ，如图1所示：则∠EHF ＝90°＝∠ABE ， ∵∠AEF ＝∠ABE ＝90°，∴∠BAE +∠AEB ＝90°，∠FEH +∠AEB ＝90°， ∴∠FEH ＝∠BAE ，在△EFH 和△ABE 中，EHF ABE FEH BAE AE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△EFH ≌△ABE （AAS ）， ∴FH ＝BE ，EH ＝AB ＝BC ， ∴CH ＝BE ＝FH ， ∵∠FHC ＝90°， ∴∠FCN ＝45°．（3）当点E 由B 向C 运动时，∠FCN 的大小总保持不变，理由如下： 作FH ⊥MN 于H ，如图2所示：由已知可得∠EAG ＝∠BAD ＝∠AEF ＝90°，结合（1）（2）得：△EFH ≌△GAD ，△EFH ∽△ABE ， ∴EH ＝AD ＝BC ＝8， ∴CH ＝BE ， ∴EH FH FHAB BE CH==； 在Rt △FEH 中，tan ∠FCN ＝8463FH EH CH AB ===， ∴当点E 由B 向C 运动时，∠FCN 的大小总保持不变，tan ∠FCN ＝43． 【点睛】本题是四边形综合题目，考查了正方形，矩形的判定及全等三角形的判定方法等知识点的综合运用，其重点是通过证三角形全等或相似来得出线段的相等或成比例．6．如图，在平面直角坐标系xOy 中，抛物线y ＝﹣14x 2+bx +c 与直线y ＝12x ﹣3分别交x 轴、y 轴上的B 、C 两点，设该抛物线与x 轴的另一个交点为点A ，顶点为点D ，连接CD 交x 轴于点E ．（1）求该抛物线的表达式及点D 的坐标； （2）求∠DCB 的正切值；（3）如果点F 在y 轴上，且∠FBC ＝∠DBA +∠DCB ，求点F 的坐标．【答案】（1）21y 234x x =-+-，D （4，1）；（2）13；（3）点F 坐标为（0，1）或（0，﹣18）． 【解析】 【分析】 （1）y ＝12x ﹣3，令y ＝0，则x ＝6，令x ＝0，则y ＝﹣3，求出点B 、C 的坐标，将点B 、C 坐标代入抛物线y ＝﹣14x 2+bx+c ，即可求解； （2）求出则点E （3，0），EH ＝EB•sin ∠OBC ＝5，CE ＝32，则CH ＝5，即可求解；（3）分点F 在y 轴负半轴和在y 轴正半轴两种情况，分别求解即可． 【详解】 （1）y ＝12x ﹣3，令y ＝0，则x ＝6，令x ＝0，则y ＝﹣3， 则点B 、C 的坐标分别为（6，0）、（0，﹣3），则c ＝﹣3， 将点B 坐标代入抛物线y ＝﹣14x 2+bx ﹣3得：0＝﹣14×36+6b ﹣3，解得：b ＝2， 故抛物线的表达式为：y ＝﹣14x 2+2x ﹣3，令y ＝0，则x ＝6或2， 即点A （2，0），则点D （4，1）； （2）过点E 作EH ⊥BC 交于点H ，C 、D 的坐标分别为：（0，﹣3）、（4，1）， 直线CD 的表达式为：y ＝x ﹣3，则点E （3，0）， tan ∠OBC ＝3162OC OB ==，则sin ∠OBC 5，则EH ＝EB•sin ∠OBC 5CE＝32，则CH＝5，则tan∠DCB＝13 EHCH=；（3）点A、B、C、D、E的坐标分别为（2，0）、（6，0）、（0，﹣3）、（4，1）、（3，0），则BC＝35，∵OE＝OC，∴∠AEC＝45°，tan∠DBE＝164-＝12，故：∠DBE＝∠OBC，则∠FBC＝∠DBA+∠DCB＝∠AEC＝45°，①当点F在y轴负半轴时，过点F作FG⊥BG交BC的延长线与点G，则∠GFC＝∠OBC＝α，设：GF＝2m，则CG＝GFtanα＝m，∵∠CBF＝45°，∴BG＝GF，即：5＝2m，解得：m＝5CF22GF CG+5＝15，故点F（0，﹣18）；②当点F在y轴正半轴时，同理可得：点F（0，1）；故：点F坐标为（0，1）或（0，﹣18）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、解直角三角形等相关知识，其中（3），确定∠FBC ＝∠DBA+∠DCB ＝∠AEC ＝45°，是本题的突破口．7．已知AB 是⊙O 的直径，弦CD ⊥AB 于H ，过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ，切点为G ，连接AG 交CD 于K ． （1）如图1，求证：KE ＝GE ； （2）如图2，连接CABG ，若∠FGB ＝12∠ACH ，求证：CA ∥FE ； （3）如图3，在（2）的条件下，连接CG 交AB 于点N ，若sin E ＝35，AK ＝10，求CN 的长．【答案】（1）证明见解析；（2）△EAD 是等腰三角形．证明见解析；（3201013【解析】 试题分析：（1）连接OG ，则由已知易得∠OGE=∠AHK=90°，由OG=OA 可得∠AGO=∠OAG ，从而可得∠KGE=∠AKH=∠EKG ，这样即可得到KE=GE ；（2）设∠FGB=α，由AB 是直径可得∠AGB=90°，从而可得∠KGE=90°-α，结合GE=KE 可得∠EKG=90°-α，这样在△GKE 中可得∠E=2α，由∠FGB=12∠ACH 可得∠ACH=2α，这样可得∠E=∠ACH ，由此即可得到CA ∥EF ； （3）如下图2，作NP ⊥AC 于P ，由（2）可知∠ACH=∠E ，由此可得sinE=sin ∠ACH=35AH AC =，设AH=3a ，可得AC=5a ，CH=4a ，则tan ∠CAH=43CH AH =，由（2）中结论易得∠CAK=∠EGK=∠EKG=∠AKC ，从而可得CK=AC=5a ，由此可得HK=a ，tan ∠AKH=3AHHK=，10a ，结合10可得a=1，则AC=5；在四边形BGKH 中，由∠BHK=∠BKG=90°，可得∠ABG+∠HKG=180°，结合∠AKH+∠GKG=180°，∠ACG=∠ABG 可得∠ACG=∠AKH ， 在Rt △APN 中，由tan ∠CAH=43PN AP=，可设PN=12b ，AP=9b ，由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ，由此可得AC=AP+CP=13b =5，则可得b=513，由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析：（1）如图1，连接OG ．∵EF 切⊙O 于G ， ∴OG ⊥EF ，∴∠AGO+∠AGE=90°， ∵CD ⊥AB 于H ， ∴∠AHD=90°， ∴∠OAG=∠AKH=90°， ∵OA=OG ， ∴∠AGO=∠OAG ， ∴∠AGE=∠AKH ， ∵∠EKG=∠AKH ， ∴∠EKG=∠AGE ， ∴KE=GE ． （2）设∠FGB=α， ∵AB 是直径， ∴∠AGB=90°，∴∠AGE =∠EKG=90°﹣α， ∴∠E=180°﹣∠AGE ﹣∠EKG=2α，∵∠FGB=12∠ACH ， ∴∠ACH=2α， ∴∠ACH=∠E ， ∴CA ∥FE ．（3）作NP ⊥AC 于P ． ∵∠ACH=∠E ， ∴sin ∠E=sin ∠ACH=35AH AC =，设AH=3a ，AC=5a ， 则224AC CH a -=，tan ∠CAH=43CH AH =， ∵CA ∥FE ， ∴∠CAK=∠AGE ， ∵∠AGE=∠AKH ，∴∠CAK=∠AKH，∴AC=CK=5a，HK=CK﹣CH=4a，tan∠AKH=AHHK =3，AK=2210AH HK a+=，∵AK=10，∴1010a=，∴a=1．AC=5，∵∠BHD=∠AGB=90°，∴∠BHD+∠AGB=180°，在四边形BGKH中，∠BHD+∠HKG+∠AGB+∠ABG=360°，∴∠ABG+∠HKG=180°，∵∠AKH+∠HKG=180°，∴∠AKH=∠ABG，∵∠ACN=∠ABG，∴∠AKH=∠ACN，∴tan∠AKH=tan∠ACN=3，∵NP⊥AC于P，∴∠APN=∠CPN=90°，在Rt△APN中，tan∠CAH=43PNAP=，设PN=12b，则AP=9b，在Rt△CPN中，tan∠ACN=PNCP=3，∴CP=4b，∴AC=AP+CP=13b，∵AC=5，∴13b=5，∴b=513，∴CN=22PN CP+=410b⋅=2010 13．8．如图，AB为⊙O的直径，P是BA延长线上一点，CG是⊙O的弦∠PCA＝∠ABC，CG⊥AB，垂足为D(1)求证：PC是⊙O的切线；(2)求证：PA AD PC CD；(3)过点A作AE∥PC交⊙O于点E，交CD于点F，连接BE，若sin∠P＝35，CF＝5，求BE的长．【答案】（1）见解析；（2）BE=12．【解析】【分析】（1）连接OC，由PC切⊙O于点C，得到OC⊥PC，于是得到∠PCA+∠OCA=90°，由AB为⊙O的直径，得到∠ABC+∠OAC=90°，由于OC=OA，证得∠OCA=∠OAC，于是得到结论；（2）由AE∥PC，得到∠PCA=∠CAF根据垂径定理得到弧AC=弧AG，于是得到∠ACF=∠ABC，由于∠PCA=∠ABC，推出∠ACF=∠CAF，根据等腰三角形的性质得到CF=AF，在R t△AFD中，AF=5，sin∠FAD=35，求得FD=3，AD=4，CD=8，在R t△OCD中，设OC=r，根据勾股定理得到方程r2=（r-4）2+82，解得r=10，得到AB=2r=20，由于AB为⊙O的直径，得到∠AEB=90°，在R t△ABE中，由sin∠EAD=35，得到BEAB＝35，于是求得结论．【详解】（1）证明：连接OC，∵PC切⊙O于点C，∴OC⊥PC，∴∠PCO=90°，∴∠PCA+∠OCA=90°，∵AB为⊙O的直径，∴∠ACB=90°，∴∠ABC+∠OAC=90°，∵OC=OA，∴∠OCA=∠OAC，∴∠PCA=∠ABC；（2）解：∵AE∥PC，∴∠PCA=∠CAF，∵AB⊥CG，∴弧AC=弧AG，∴∠ACF=∠ABC，∵∠PCA=∠ABC，∴∠ACF=∠CAF，∴CF=AF，∵CF=5，∴AF=5，∵AE∥PC，∴∠FAD=∠P，∵sin∠P=35，∴sin∠FAD=35，在R t△AFD中，AF=5，sin∠FAD=35，∴FD=3，AD=4，∴CD=8，在R t△OCD中，设OC=r，∴r2=（r﹣4）2+82，∴r=10，∴AB=2r=20，∵AB为⊙O的直径，∴∠AEB=90°，在R t△ABE中，∵sin∠EAD=35，∴35BEAB，∵AB=20，∴BE=12．【点睛】本题考查切线的性质，锐角三角函数，圆周角定理，等腰三角形的性质，解题关键是连接OC构造直角三角形．9．我市在创建全国文明城市的过程中，某社区在甲楼的A处与E处之间悬挂了一副宣传条幅，在乙楼顶部C点测得条幅顶端A点的仰角为45°，条幅底端E点的俯角为30°，若甲、乙两楼之间的水平距离BD为12米，求条幅AE的长度．(结果保留根号)【答案】AE 的长为(123)+ 【解析】 【分析】在Rt ACF 中求AF 的长, 在Rt CEF 中求EF 的长,即可求解. 【详解】过点C 作CF AB ⊥于点F 由题知：四边形CDBF 为矩形12CF DB ∴==在Rt ACF 中，45ACF ∠=︒tan 1AFACF CF∴∠== 12AF ∴=在Rt CEF 中，30ECF ∠=︒ tan EFECF CF∴∠= 3123EF ∴=43EF ∴=1243AE AF EF ∴=+=+∴求得AE 的长为(1243+【点睛】本题考查了三角函数的实际应用,中等难度,作辅助线构造直角三角形是解题关键.10．已知：如图，在Rt △ABO 中，∠B =90°，∠OAB =30°，OA =3．以点O 为原点，斜边OA 所在直线为x 轴，建立平面直角坐标系，以点P （4，0）为圆心，PA 长为半径画圆，⊙P 与x 轴的另一交点为N ，点M 在⊙P 上，且满足∠MPN =60°．⊙P 以每秒1个单位长度的速度沿x 轴向左运动，设运动时间为ts ，解答下列问题： （发现）（1）MN 的长度为多少；（2）当t =2s 时，求扇形MPN （阴影部分）与Rt △ABO 重叠部分的面积．（探究）当⊙P 和△ABO 的边所在的直线相切时，求点P 的坐标．（拓展）当MN 与Rt △ABO 的边有两个交点时，请你直接写出t 的取值范围．【答案】【发现】（1）MN 的长度为π3；（23P 的坐标为10（，）；或230）或230（）；【拓展】t 的取值范围是23t ≤＜或45t ≤＜，理由见解析．【解析】 【分析】发现：（1）先确定出扇形半径，进而用弧长公式即可得出结论； （2）先求出PA =1，进而求出PQ ，即可用面积公式得出结论； 探究：分圆和直线AB 和直线OB 相切，利用三角函数即可得出结论；拓展：先找出MN 和直角三角形的两边有两个交点时的分界点，即可得出结论． 【详解】 [发现]（1）∵P （4，0），∴OP =4． ∵OA =3，∴AP =1，∴MN 的长度为6011803ππ⨯=． 故答案为3π； （2）设⊙P 半径为r ，则有r =4﹣3=1，当t =2时，如图1，点N 与点A 重合，∴PA =r =1，设MP 与AB 相交于点Q ．在Rt △ABO 中，∵∠OAB =30°，∠MPN =60°． ∵∠PQA =90°，∴PQ 12=PA 12=，∴AQ =AP ×cos30°3=∴S 重叠部分=S △APQ 12=PQ ×AQ 3= 即重叠部分的面积为38． [探究]①如图2，当⊙P 与直线AB 相切于点C 时，连接PC ，则有PC ⊥AB ，PC =r =1． ∵∠OAB =30°，∴AP =2，∴OP =OA ﹣AP =3﹣2=1； ∴点P 的坐标为（1，0）；②如图3，当⊙P 与直线OB 相切于点D 时，连接PD ，则有PD ⊥OB ，PD =r =1，∴PD ∥AB ，∴∠OPD =∠OAB =30°，∴cos ∠OPD PD OP =，∴OP 123303cos ==︒，∴点P 的坐标为（233，0）； ③如图4，当⊙P 与直线OB 相切于点E 时，连接PE ，则有PE ⊥OB ，同②可得：OP 233=； ∴点P 的坐标为（233-，0）；[拓展]t 的取值范围是2＜t ≤3，4≤t ＜5，理由：如图5，当点N 运动到与点A 重合时，MN 与Rt △ABO 的边有一个公共点，此时t =2； 当t ＞2，直到⊙P 运动到与AB 相切时，由探究①得：OP =1，∴t 411-==3，MN 与Rt △ABO 的边有两个公共点，∴2＜t ≤3．如图6，当⊙P 运动到PM 与OB 重合时，MN 与Rt △ABO 的边有两个公共点，此时t =4； 直到⊙P 运动到点N 与点O 重合时，MN 与Rt △ABO 的边有一个公共点，此时t =5； ∴4≤t ＜5，即：t 的取值范围是2＜t ≤3，4≤t ＜5．【点睛】本题是圆的综合题，主要考查了弧长公式，切线的性质，锐角三角函数，三角形面积公式，作出图形是解答本题的关键．。

2014届高考数学“得分题”训练05解析版命题报告：三角函数的性质周期性、单调性. 16随机事件的概率.17直线与平面垂直、点到平面的距离、等体积法一、选择题（每小题5分，共10小题）1．（2014届某某省某某市高中毕业年级第一次质量预测）已知集合{|2}A x x =>，{|}B x x m =<，且A B R =，那么m 的值可以是（ ）A ．0B ．1C ．2D ．3 【答案】D 【解析】∵{|}B x x m =<,且AB R =,∴2m >.2．（2014届某某省某某市重点中学高三12月月考）下列有关命题的说法正确的是（ ） A.命题“若12=x ，则1=x ”的否命题为“若12=x ，则1≠x ” B.命题“01,2<-+∈∃x x R x ”的否定是“01,2>-+∈∀x x R x ” C.命题“若y x =，则y x sin sin =”的逆否命题为假命题 D.若“p 或q ”为真命题，则p ，q 至少有一个为真命题3．（2014届某某市七校联盟高三上学期联考）函数f(x)=3x ++）（x -6lg 1的定义域是（ ）A ．{}|6x x > B. {}|36x x -<≤C ．{}|3x x >-D ． ｛x ｜-3≤x <6且x ≠5｝4．（2014届某某市杨浦区高三上学期学业质量调研）设锐角ABC ∆的三内角A 、B 、C 所对边的边长分别为a 、b 、c ，且1=a ，A B 2=,则b 的取值X 围为（ ）. A.()3,2 B.()3,1 C.()2,2 D.()2,05．（2014届某某某某重点中学高三上学期第三次月考）已知ABC ∆是边长为2的正三角形,B 为线段EF 的中点,且3=EF ,则AF AC AE AB ⋅+⋅的取值X 围是（ ） A.[]3,0 B.[]6,3 C. []9,6 D.[]9,3所以原式22AB BA BE AB BA BF BA BC BC BF =-⋅+-⋅-⋅+⋅4cos 4cos 2cos BA BE ABE BA BF ABF BC BF CBF=-⋅∠+-⋅∠-+⋅∠63(cos cos cos )ABE ABF CBF =-∠+∠+∠设ABE θ∠=，则ABF πθ∠=-.6．（2014届某某市十三校高三12月联考）如果a b c 、、满足c b a <<，且0ac <，那么下列选项不恒成立的是（ ）．（A ）ab ac > （B ）22cb ab < （C ）()0c b a -> （D ）()0ac a c -< 【答案】B 【解析】c a <且0ac <，故0,0c a <>，由不等式的性质知A ，C ，D 都恒成立，只有B 不恒成立，故选B ．7．（2014届某某稳派教育高三上学期强化训练）某几何体的三视图如图所示，则该几何体的体积为（ ）A.310π B. 320πC.π4D.π68．（2014届某某某某金台区高三11月会考）在如程序框图中，若0()x f x xe =，则输出的是（ ）A.2014xxe xe + B.2012xxe xe + C.2013xxe xe + D.2013xe x +9．（2014届某某省某某市某某五中高三12月月考）已知{}n a 为等差数列，{}n b 为等比数列，其公比1≠q 且),,2,1(0n i b i =>,若111111,b a b a ==，则（ ） A.66b a > B.66b a =C.66b a <D.66b a <或66b a > 【答案】A 【解析】 ∵11162a a a +=，6111111b bb a a ==，∴1111112a a a a +>，∴66ab >. 10．（2014届某某某某九中高三上学期第五次月考）若)1,2(-P 为圆25)1(22=+-y x 的弦AB 的中点，则直线AB 的方程（ ） A. 03=--y x B. 032=-+y x C. 01=-+y x D. 052=--y x二、填空题11．（2014届某某省某某市实验高中高三11月阶段考试）某社区有600个家庭，其中高收入家庭150户，中等收入家庭360户，低收入家庭90户，为了调查购买力的某项指标，用分层抽样的方法从中抽取一个容量为80的样本，则中等收入家庭应抽取的户数是.12．（2014届某某省某某一中高三上学期入学摸底）若(2)a i i b i -=-，其中,a b R ∈，i 是虚数单位，则复数a bi += 【答案】12i -+ 【解析】若(2)a i i b i -=-，则i b ai -=+2，所以2,1=-=b a ，于是i bi a 21+-=+.13．（2014届某某某某第一中学高三上学期第二次月考）曲线2-=x xy 在点（1，-1）处的切线方程为.14．（2014届某某阜宁中学高三上学期第三次调研测试）若对于给定的负实数k ，函数()k f x x=的图象上总存在点C ，使得以C 为圆心，1为半径的圆上有两上不同的点到原点的距离为2，则k 的取值X 围为.三、解答题15．（2014届某某省揭阳一中高三上学期第二次段考）函数R x Z k x k x x f ∈∈-++-=,,)2214cos()2cos()(π.（1）求)(x f 的周期；（2）)(x f 在),0[π上的减区间；（3）若=)(αf 5102，)2,0(πα∈，求)42tan(πα+的值.∴)42tan(πα+1731724117244tan 2tan 14tan2tan -=-+=-+=παπα.16．（2014届某某某某外国语学校高三12月月考）一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4。