下载文档原格式
高中数学复习讲义一、代数1.1 一元一次方程1.2 一元二次方程1.3 平面直角坐标系1.4 解析几何与向量1.5 指数与对数1.6 三角函数与三角恒等变换1.7 数列与数学归纳法二、几何2.1 平面与立体几何基本概念2.2 直线与角2.3 三角形与三角形的性质2.4 四边形与四边形的性质2.5 圆与圆的性质2.6 空间几何与立体几何三、概率与统计3.1 随机事件与概率的计算3.2 组合与排列3.3 抽样与统计四、数学思想方法4.1 推理与证明4.2 逻辑与谬误4.3 数学建模与解题策略五、应用题本讲义将针对高中数学涵盖的主要内容进行复习总结，旨在帮助大家全面复习数学知识，掌握解题方法和技巧，为高考做好充分准备。
一、代数1.1 一元一次方程一元一次方程是数学中最基础的方程形式之一，解一元一次方程需要掌握方程的基本性质和求解方法。
我们将重点讲解常见的一元一次方程类型，并提供解题思路和方法。
掌握一元一次方程的求解技巧对于解决实际问题具有重要意义。
1.2 一元二次方程一元二次方程在高中数学中起着重要的作用，解一元二次方程需要掌握配方法、因式分解法以及求根公式等知识点。
我们将介绍一元二次方程的基本概念和解法，并通过大量例题帮助大家提高解题能力。
1.3 平面直角坐标系平面直角坐标系是研究平面几何和解析几何的基础，了解坐标系的性质和坐标变换的规律对于解决几何问题至关重要。
我们将详细介绍直角坐标系的相关概念和性质，并结合实例进行讲解，帮助大家掌握平面直角坐标系的应用。
1.4 解析几何与向量解析几何是将代数与几何相结合的重要数学分支，研究空间中点、直线、平面等几何对象的解析表达和性质。
向量是解析几何中的重要工具，学习向量的表示方法和运算规律有助于解决几何问题。
我们将讲解解析几何基本概念和向量的数学性质，并通过练习题提高大家的解题能力。
1.5 指数与对数指数和对数是高中数学中重要的数学工具和运算方法，涉及到数学表达式的简化、方程的求解等。
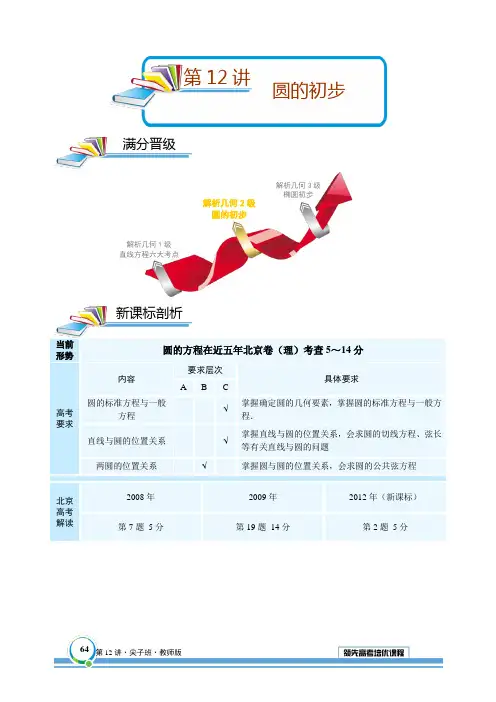
当前形势圆的方程在近五年北京卷（理）考查5～14分高考要求内容要求层次具体要求A B C圆的标准方程与一般方程√掌握确定圆的几何要素，掌握圆的标准方程与一般方程．直线与圆的位置关系√掌握直线与圆的位置关系，会求圆的切线方程、弦长等有关直线与圆的问题两圆的位置关系√掌握圆与圆的位置关系，会求圆的公共弦方程北京高考解读2008年2009年2012年（新课标）第7题5分第19题14分第2题5分新课标剖析满分晋级第12讲解析几何1级直线方程六大考点解析几何2级圆的初步解析几何3级椭圆初步圆的初步【教师备案】因为直线方程建议讲了4小时，所以本讲建议讲2小时考点1：圆的标准方程1. 圆的标准方程 ⑴以点()C a b ，为圆心，r 为半径的圆的方程：222()()x a y b r -+-= ⑵圆心在原点的圆的标准方程：222x y r +=【教师备案】⑴我们知道，平面内到一定点的距离等于定长的点的轨迹是圆，定点是圆心，定长是圆的半径．现在我们来求以()C a b ，为圆心，r 为半径的圆的方程．设()M x y ，是C e 上的任意一点．点M 在C e 上的条件是CM r =．也就是说，如果点M 在C e 上，则CM r =，反之，如果CM r =，则点M 在C e 上．由两点间的距离公式，所说条件可转化为方程表示：()()22x a y b r -+-=．两边平方，得()()222x a y b r -+-=①．显然，C e 上任意一点M 的坐标()x y ，适合方程①；如果平面上一点M 的坐标()x y ，适合方程①，可得CM r =，则点M 在C e 上．因此方程①是以点()C a b ，为圆心，r 为半径的圆的方程，叫做圆的标准知识切片知识点睛12.1圆的方程M COyxP (x, y )r Oy x方程．特别地，如果圆心在坐标原点，这时00a b ==，，圆的标准方程就是222x y r +=． ⑵圆的标准方程()()222x a y b r -+-=⇔圆心()a b ，，半径为r ，它体现了圆的几何性质，圆的标准方程直接给出了圆的圆心坐标和半径长，突出了确定一个圆的基本要素，因此， 有利于画出图形．⑶圆的标准方程中共有三个待定系数a b r ，，，只要确定出这三个量的值，圆的方程即被 确定．因此确定圆的方程需要三个独立的条件，其中圆心是圆的定位条件，半径是圆的 定形条件．⑷方程()()22x a y b t -+-=：①当0t >时，表示圆心为()C a b ，t ②当0t =时，表示一个点()C a b ，； ③当0t <时，不表示任何图形．2. 点与圆的位置关系圆的标准方程()()222x a y b r -+-=，圆心()A a b ，，半径r ， 若点()00M x y ，在圆上，则()()22200x a y b r -+-=； 若点()00M x y ，在圆外，则()()22200x a y b r -+->；若点()00M x y ，在圆内，则()()22200x a y b r -+-<；反之，也成立．【教师备案】判断点与圆的位置的方法是由两点间的距离公式，求出该点到圆心的距离，再与圆的半径比较大小即可．例：写出圆心为()23A -，，半径长等于5的圆的标准方程，并判断点()157M -，，()251M --是否在这个圆上，若不在这个圆上，是在圆内还是在圆外？【解析】 圆心为()23A -，，半径长等于5的圆的标准方程是()()222325x y -++=．把()157M -，的坐标代入上述方程中，有()()22527325-+-+=，即点1M 的坐标适合圆的方程，可知点1M 在这个圆上；把()251M -的坐标代入上述方程中，有()()225213134525--+-+=+，可知点2M 不在这个圆上，而在这个圆内．3. 确定圆的方法要求出圆的标准方程必须求出圆心和半径．确定圆的标准方程的主要方法是待定系数法，即列出a b r ，，的方程组，一般步骤为： ⑴根据题意，设所求的圆的标准方程()()222x a y b r -+-=；⑵根据已知条件，建立关于a b r ，，的方程组； ⑶解方程组，求出a b r ，，的值，并把它们代入所设的圆的方程中，就得到所求圆的方程． 条件 方程形式过原点 ()()()2222220x a y b a b a b -+-=++≠ 圆心在x 轴上 ()()2220x a y r r -+=≠圆心在y 轴上 ()()22220x y b r r +-=≠圆心在x 轴上且过原点()()2220x a y a a -+=≠圆心在y 轴上且过原点()()2220x y b b b +-=≠与x 轴相切 ()()()2220x a y b b b -+-=≠与y 轴相切 ()()()2220x a y b a a -+-=≠与两坐标轴都相切()()()2220x a y b a a b -+-==≠【例1】 圆的标准方程写出下列各圆的方程⑴经过点()63，，圆心为()22-，；⑵经过点()45A --，，()61B -，，且以线段AB 为直径．【解析】 ⑴所求圆的方程为()()222241x y -++=⑵所求圆的方程为()()221329x y -++=【备选】求以两直线1:5l x y -=，2:24l x y +=的交点为圆心，且与x 轴相切的圆的标准方程．【解析】 所求圆的标准方程为()()22324x y -++=．考点2：圆的一般方程1． 圆的一般方程220x y Dx Ey F ++++=，（2240D E F +->）说明：⑴2x 和2y 项的系数相等且都不为零；⑵没有xy 这样的二次项．⑶表示以,22D E ⎛⎫-- ⎪⎭为圆心，22142D E F +-为半径的圆．例：二元二次方程22232340x y x y +-++=是否表示圆．【解析】 ∵2x 和2y 的系数不相等，∴方程不表示圆．【教师备案】将圆的标准方程()()222x a y b r -+-=展开，得22222220x y ax by a b r +--++-=，由此可见，圆的方程具有如下形式：()220x y Dx Ey F ++++=*，其中D E F ，，为常数．那么，形如()*的方程是否都表示圆呢？将方程220x y Dx Ey F ++++=配方，得()222214224D E x y D E F ⎛⎫⎛⎫+++=+- ⎪ ⎪⎝⎭⎝⎭，与圆的标准方程比较，可知：经典精讲知识点睛①当2240D E F +->时，方程()*表示以22DE ⎛⎫-- ⎪⎝⎭，为圆心，22142D EF +-为半径的圆；②当2240D E F +-=时，方程()*只有一个解，表示一个点22DE ⎛⎫-- ⎪⎝⎭，；③当2240D E F +-<时，方程()*无实数解，它不表示任何图形．例：若220x y x y m +-+-=表示一个圆的方程，则m 的取值范围是（ ）A ．12m >-B ．12m -≥ C ．12m <- D ．2m >-【解析】 A2． 如何选用圆的方程圆的方程有标准方程和一般方程，求哪一种都需要三个独立条件，都要用到待定系数法，但要灵活选用圆的方程的形式，以便简化计算．一般来说．⑴如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径来列方程的问题一般采用圆的标准方程，再用待定系数法求出a b r ，，；⑵如果已知条件和圆心或半径都无直接关系，一般采用圆的一般方程，再利用待定系数法求出常数D E F ，，．例：⑴求经过两点()14A -，、()32B ，且圆心在y 轴上的圆的方程；⑵求过三点(11)A -，，(14)B ，，(42)C -，的圆的方程，并求这个圆的半径和圆心坐标． 【解析】 ⑴ 圆的方程是()22110x y +-=．⑵所求圆的方程为227320x y x y +--+=． 半径522r =，圆心7322⎛⎫⎪⎝⎭，【教师备案】老师可以配合知识点睛中的例子先讲圆的一般方程以及一般方程表示圆的条件，然后让学生做例2以及相应班次的学案；最后再根据知识点睛中的例子讲如何选用圆的方程，然后再做例3和相应班次的学案．【例2】 方程220x y Dx Ey F ++++=表示圆的条件判断下列方程是否表示圆，若是，求出圆心和半径⑴ 22104x y x +-+=；⑵ ()22200x y ax a ++=≠；⑶ 22210x y ay ++-=；【追问】若表示圆，则当圆的面积最小时，a 的值为多少？ ⑷ 22220160x y x +++=．经典精讲⑸ 224250x y mx y m ++-+=【解析】 解法一：⑴22102x y ⎛⎫-+= ⎪⎝⎭表示一个点，坐标为102⎛⎫⎪⎝⎭，；⑵()()2220x a y a a ++=≠表示圆，圆心()0a -，，半径r a =； ⑶()2221x y a a ++=+表示圆，圆心()0a -，，半径21r a =+； 【追问】当0a =时，圆的面积取最小值． ⑷()22221010160x y ++=-<，不表示任何图形． ⑸1m >或14m <时表示圆，圆心为()21m -，，半径为2451m m -+． 当114m ≤≤时，方程不表示圆．【备选】若直线530x y -+=经过圆2222104m x y mx y +-++-=的圆心，则m 等于（ ）A ．16-B ．16C ．0或16D ．0或16-【解析】 A【例3】求圆的一般方程⑴已知ABC △三边所在直线方程:60AB x -=，:280BC x y --=，:20CA x y +=，求此三 角形外接圆的方程．⑵求过原点及()11A ，且在x 轴上截得的线段长为3的圆的方程． 【解析】 ⑴222143002x y x y +-++=． ⑵所求圆的方程为22350x y x y ++-=或2230x y x y +-+=．考点3：直线与圆的位置关系1．直线与圆的位置关系：①直线与圆相交，有两个公共点； ②直线与圆相切，有一个公共点；知识点睛12.2直线（圆）与圆的位置关系③直线与圆相离，没有公共点．2．直线与圆的位置关系的判定有两种方法：①代数法：判断直线0Ax By C ++=和圆220x y Dx Ey F ++++=的位置关系，可将2200Ax By C x y Dx Ey F ++=⎧⎨++++=⎩消去y （或x ），得20mx nx p ++=（或20my ny p ++=）． 当0∆>时，直线与圆相交，有两个公共点； 当0∆=时，直线与圆相切，有一个公共点； 当0∆<时，直线与圆相离，无公共点．②几何法：已知直线0Ax By C ++=和圆()()222x a y b r -+-=，可用圆心到直线的距离22Aa Bb Cd A B++=+与r 的大小关系判断直线与圆的位置关系．当d r <时，直线与圆相交，有两个公共点； 当d r =时，直线与圆相切，有一个公共点； 当d r >时，直线与圆相离，无公共点；<教师备案>一般的，判定直线与圆的位置关系都用几何法，代数法在圆锥曲线才会常用。
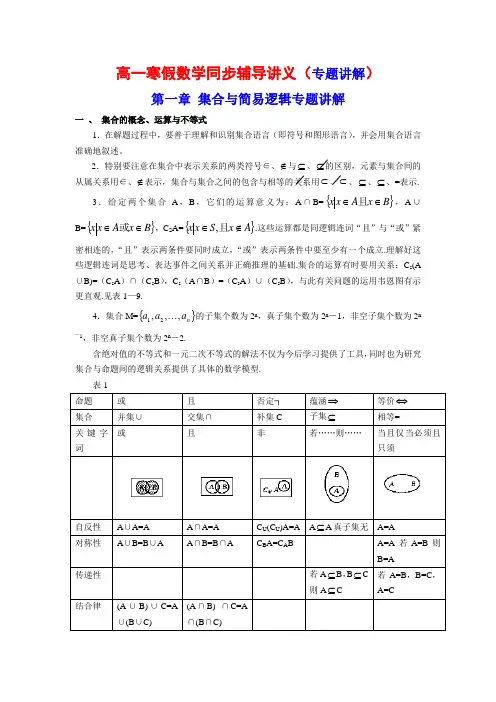
高一寒假数学同步辅导讲义（专题讲解）第一章 集合与简易逻辑专题讲解一 、 集合的概念、运算与不等式1．在解题过程中，要善于理解和识别集合语言（即符号和图形语言），并会用集合语言准确地叙述。
2．特别要注意在集合中表示关系的两类符号∈、∉与⊆、⊆的区别，元素与集合间的从属关系用∈、∉表示，集合与集合之间的包含与相等的关系用⊂、⊂、⊆、⊆、=表示.3．给定两个集合A ，B ，它们的运算意义为：A ∩B={}B x A x x ∈∈且，A ∪B={}B x A x x ∈∈或，C S A={}A x S x x ∉∈且,.这些运算都是同逻辑连词“且”与“或”紧密相连的，“且”表示两条件要同时成立，“或”表示两条件中要至少有一个成立.理解好这些逻辑连词是思考、表达事件之间关系并正确推理的基础.集合的运算有时要用关系：C s (A ∪B)=（C s A ）∩（C sB ），C s （A ∩B ）=（C s A ）∪（C s B ），与此有关问题的运用韦恩图有示更直观.见表1—9.4．集合M={}n a a a ,,,21 的子集个数为2n ，真子集个数为2n －1，非空子集个数为2n—1，非空真子集个数为2n －2.含绝对值的不等式和一元二次不等式的解法不仅为今后学习提供了工具，同时也为研究集合与命题间的逻辑关系提供了具体的数学模型.表1 命题 或 且 否定┐ 蕴涵⇒ 等价⇔ 集合 并集∪ 交集∩ 补集C 子集⊆ 相等=关键字词 或且非若……则……当且仅当必须且只须自反性 A ∪A=A A ∩A=A C U (C U )A=A A ⊆A 真子集无 A=A 对称性A ∪B=B ∪AA ∩B=B ∩AC B A=C A BA=A 若A=B 则B=A传递性若A ⊆B ，B ⊆C 则A ⊆C若A=B ，B=C ，A=C 结合律(A ∪B)∪C=A ∪(B ∪C)(A ∩B) ∩C=A ∩(B ∩C)【例1】 已知集合M=R x x y y ∈+=,12，N={}R x x y y ∈+=,1，则M ∩N=（ ） A ．（0，1）（1，2） B ．{})2,1(),1,0( C ．{}21==y y y 或 D ．{}1≥y y分析 集合M 、N 是用描述法表示的，元素是实数y 而不是实数对（x ，y ），因此M ，N 分别表示函数y=x 2+1（x ∈R ），y=x+1（x ∈R ）的值域，求M ∩N 即求两函数值域的交集.解 M={}R x x y y ∈+=,12={}1≥y y ，N={}R x x y y ∈+=,1={}R y y ∈. ∴M ∩N={}1≥y y ∩{}R y y ∈={}1≥y y ，故选D.说明（1）本题求M ∩N.经常发生解方程组⎩⎨⎧-=+=112x y x y 得⎩⎨⎧==10y x 或⎩⎨⎧==21y x 从而选B 错误，这是由于在集合概念的理解上，仅注意了构成集合元素的共同属性，而忽视了集合的元素是什么，事实上M ，N 的元素是数而不是点，因此M 、N 是数集而不是点集.（2）集合是由元素构成的，认识集合要从认识元素开始，要注意区分{}R x xy x ∈+=,12，{}R x x y y ∈+=,12，{}R x x y y x ∈+=,1),(2这三个集合是不同的.【例2】给出下面元素与集合或集合之间的关系：（1）0⊂{}0；（2）0∈{}0；（3）Φ∈{}Φ；（4）a ∈{}a ；（5）Φ={}0；（6）{}0∈Φ；（7）Φ∈{}0；（8）Φ⊂{}0，其中正确的是（ ）A ．（2）（3）（4）（8）B ．（1）（2）（4）（5）C ．（2）（3）（4）（6）D ．（2）（3）（4）（7） 分析 依次判断每个关系是否正确，同时用排除法筛选.解 （1）应为0∈{}0；（2）（3）（4）正确，排除B ，再看（6）（7）（8）哪个正确，由Φ是{}0的子集，因此（8）正确，故选A.说明 0与{}0只有一种关系：0∈{}0 ；R 与{}R ；Φ与{}0也只有一种关系：Φ⊂{}0. 【例3】 已知集合A={}R x x m x x ∈=+++,01)2(2，若A ∩R +=Φ，则实数m 的取值范围是__________.分析 从方程观点看，集合A 是关于x 的实系数一元二次方程x 2+(m+2)x+1=0的解集，而x=0不是方程的解，所以由A ∩R +=Φ可知该方程只有两个负根或无实数根，从而分别由判别式转化为关于m 的不等式，并解出m 的范围.解 由A ∩R +=Φ又方程x 2+(m+2)x+1=0无零根，所以该方程只有两个负根或无实数根，即⎩⎨⎧<+-≥-+=∆.0)2(04)2(2m m或△=(m+2)2－4＜0.解得m ≥0或－4＜m ＜0，即m ＞－4.说明 此题容易发生的错误是由A ∩R +=Φ只片面地推出方程只有两个负根（因为两根之积为1，因此方程无零根），而把A=Φ漏掉，因此要全面正确理解和识别集合语言.【例4】 已知集合A={}0232=+-x x x ，B={}012=-+-a ax x x ，且A ∪B=A ，则a 值为__________.分析 由A ∪B=A ⇔B ⊆A 而推出B 有四种可能，进而求出a 的值. 解 ∵A ∪B=A ， ∴B ⊆A ，∵A={}2,1，∴B=Φ或B={}1或B={}2或B={}2,1. 若B=Ø，则令△＜0得a ∈Ø；若B ={}1，则令△=0得a=2，此时1是方程的根；若B={}2，则令△=0得a=2，此时2不是方程的根.∴a ∈Ø ；若B={}2,1，则令△＞0得a ∈R 且a ≠2，把x=1代入方程得a ∈R ，把x=2代入方程得a=3，综上a 的值为2或3.说明 本题不能直接写出B=（），因为a （）可能等于1，与集合元素的互异性矛盾，另外还要考虑到集合B 有可能是空集，还有可能是单元素集的情况.【例5】 命题甲：方程x 2+mx+1=0有两个根异负根；命题乙：方程4x 2+4(m －2)x+1=0无实根，这两个命题有且只有一个成立，求m 的取值范围.分析 使命题甲成立的m 的集合为A ，使命题乙成立的m 的集合而为B ，有且只有一个命题成立是求A ∩C R B 与C R A ∩B 的并集.解 因使命题甲成立的条件是△1=m 2－4＞0，且－m ＜0，所以解得m ＞2，即集合A={}2>m m ；因使命题乙成立的条件是△2=16(m －2)2－16＜0，所以解得1＜m ＜3，即集合B={}31<<m m .若命题甲、乙有且只有一个成立，则m ∈A ∩C R B 或m ∈C R A ∩B ，而A ∩C R B={}2>m m ∩{}31≥≤m m m 或={}3≥m m ，C R A ∩B={}2>m m ∩{}31<<m m ={}21≤<m m ，所以综上所求m 的范围是{}321≥≤<m m m 或.说明（1）本题体现了集合语言、集合思想的重要作用；（2）用集合语言来表示m 的满园即准备又简明.二、 一元二次方程实根的分布【例1】关于x 的方程3x 2－5x+a=0，实数a 在什么范围内，一个根大于－2，而小于0，另一个根大于1，而小于3？解 由题意，a 应满足条件⎪⎪⎩⎪⎪⎨⎧>+⨯-⨯=<+-=<=>+-⨯--⨯=-03533)3(053)1(0)0(0)2(5)2(3)2(22a f a f a f a f 解得－12＜a ＜0.【例2】关于x 的方程2x 2+3x －5m=0，有两个小于1的实根，求实根m 的取值范围. 解 二次函数图像是开口向上的抛物线，对称轴x=－43，在x=1的左侧.这样抛物线与x 轴有两个交点的横坐标都小于1，所以应满足的条件是：⎩⎨⎧≥-=∆>-+=04090532)1(m m f 解得－409≤m ＜1. 【例3】关于x 的方程x 2―2tx+t 2―1=0的两个根介于―2和4之间，求实数t 的取值范围.解 由题意可知，t 需满足⎪⎪⎪⎩⎪⎪⎪⎨⎧<=-<->=--=∆>+-=>++=-42204)1(440158)4(034)2(2222t a b t t t t f t t f 解得 －1＜t ＜3.说明 讨论二次方程实根的分布，常有以下一些结论（设方程f(x)=ax 2+bx+c=0（a ＞0）两实根为x 1，x 2）：（1）若m ＜x 1＜n ＜p ＜x 2＜q ，则方程系数应同时满足下列不等式组：⎪⎪⎩⎪⎪⎨⎧>++=<++=<++=>+=0)(0)(0)(0)(2222c bq aq q f c bp ap p f c bn an n f c bm am m f 特别地，当方程f(x)=0有一正根，一负根，即x 1＜0，x 2＞0，则应用f(0)=c ＜0；若方程f(x)=0有一个根大于k ，一个根小于k ，则应有f(k)＜0.（2）若二次方程f(x)=0的两面根在区间（m ，n ）内，则应同时满足⎪⎪⎪⎩⎪⎪⎪⎨⎧<-<≥∆>>n a b m n f m f 200)(0)( 特别地，若f(x)=0两根都大于k 时，则有⎪⎪⎩⎪⎪⎨⎧>-≥∆>.2,0,0)(k ab k f三、 四种命题与充要条件1．所谓命题，是指可以判断其真假的陈述语句，一个陈述语句所叙述的事情符合事实，我们称它为真命题，反之，一个陈述语句所叙述的事情违反事实，我们称它为假命题.2．命题有四种形式，即原命题、逆命题、否命题、逆否命题，其中原命题与逆否命题是等价的，逆命题与否命题是等价的。
97期末考试试卷分析：高一下学期主要讲必修5和必修3，有的学校进度会比较快，讲一点必修2，对于必修2有的学校会讲空间几何体，有的学校会讲直线．学校在高一下学期期中考试之前会把必修5讲完，所以期中考试主要是进行模块考试（必修5），所以在期末考试的时候必修3是重点，会带着考一点必修2的知识．但学校考虑到是期末考试，要对这一学期的知识进行回顾，所以一般学校会分Ⅰ卷和Ⅱ卷，Ⅰ卷主要考必修3和必修2；Ⅱ卷主要考必修5．我们本讲主要是对必修3和必修2（也就是Ⅰ卷）进行复习． 考试内容分为三个部分：算法，概率与统计，直线与圆算法：主要考查四个方面，1、求输出结果；2、填判断框；3、求输入的值；4、写程序框图．前三个以选择题或填空题的形式出现，重点是1和2，在考试中肯定有，属于比较简单的题；写程序框图主要以解答题形式出现，在考试中不一定有． 概率与统计：主要有两个大方面，1、统计；2、概率．统计主要涉及到随机抽样、频率分布直方图、茎叶图、平均数和方差．其中随机抽样重点考察分层抽样，频率分布直方图重点考察已知直方图，求频率或其它相关的问题；茎叶图主要考察已知茎叶图，求平均数和方差；这部分主要以选择题或填空题的形式出现．概率主要涉及到基本事件、古典概型和几何概型．基本事件中重点考察对立事件与互斥事件以及概率加法公式，以选择题或填空题的形式出现；古典概型是期末考试的重点，以解答题的形式出现；几何概型以选择题或解答题的形式出现．最后可能还会有概率与统计的综合题，常以解答题的形式出现．直线与圆：主要考察两个大方面，1、直线方程；2、圆的方程．直线方程主要考察直线的斜率、直线方程、直线的位置关系、距离等问题，以选择题、填空题和解答题的形式出现；圆的方程主要考察圆的两个表示形式、直线与圆的位置关系，尤其是直线与圆相切和相交、圆与圆的位置关系等，也是以选择题、填空题和解答题的形式出现．2012年高一下学期期末各部分内容所占分值比（Ⅰ卷）第15讲 期末复习981．算法的特征：⑴有穷性：算法必须在执行有限步后结束，通常还理解为实际上能够容忍的合理限度； ⑵确定性：算法的每一个步骤必须有确定的含义；⑶可行性：组成算法的每个步骤和操作必须是相当基本的，原则上都是能精确地执行的； ⑷输入：有零个或多个输入： ⑸输出：有一个或多个输出．2．算法的三种基本逻辑结构：顺序结构、条件（分支）结构和循环结构．例：⑴已知直角三角形两直角边长为a ，b ，求斜边长c 的一个算法分下列三步：①计算c =②输入直角三角形两直角边长a ，b 的值；③输出斜边长c 的值．其中正确的顺序是（ ）A ．①②③B ．②③①C ．①③②D ．②①③ ⑵下列给出的赋值语句正确的是（ ）A ．3M =B ．21(1)(1)y x x x =-=+-C ．3M M =+D ．3x y +=⑶将两个数8a =，7b =交换使7a =，8b =，使用赋值语句正确的一组是（ ）知识切片知识点睛15.1算法99A ．a b =，b a =B ．c b =，b a =，a c =C ．b a =，a b =D ．a c =，c b =，b a = 【解析】⑴ D ；⑵ C ；⑶ B ． 3．《九章算术》是中国古代的数学专著，其中的“更相减损术”可以用来求两个数的最大公约数．以具体的例子来说明更相减损术求最大公约数的原理： 以求117和182的最大公约数为例： (117182)(11765)(6552)(5213)(1339)(1326)(1313)→→→→→→，，，，，，，， 每次操作后得到的两个数与前两个数的最大公约数相同，而且逐渐减少，故总能得到相等的两个数，即为所求的最大公约数．例：2183和1947的最大公约数是________．【解析】 59；4．秦九韶算法与其它算法在计算量上面的比较：1110()n n n n f x a x a x a x a --=++++， ⑴直接求和法：先计算各个单项式的值，再把它们相加，乘法次数为(1)(1)212n n n n ++-+++=，加法次数n ；⑵逐项求和法：先计算x 的各项幂的值，再分别相乘，计算幂值需要乘法1n -次，将幂值与多项式系数k a 相乘需要乘法n 次，故共需要乘法21n -次，加法n 次．此方法对直接求和法有所改进，但仍然比秦九韶算法计算量大很多． ⑶秦九韶算法：计算量仅为乘法n 次，加法n 次．例：用“秦九韶算法”求多项式5432()254367f x x x x x x =--+-+当5x =时的值时，需要进行乘法的次数______次，需要进行加法的次数是_______次． 【解析】 55，【例1】算法⑴如果如图⑴程序框图的输出结果为18-，那么在判断框①中表示的“条件”应该是（ ） A ．9i ≥ B ．9>i C ．8i ≥ D ．11>i⑵如图⑵程序框图箭头a 指向①处时，输出s =____________．箭头a 指向②处时，输出 s =___________．⑶下图⑶是计算123100=++++S 的程序框图 ① 判断其是否正确，若有错，请指出并改正； ② 求输出的S 的值．经典精讲100图⑴ 图⑵ 图⑶⑷某程序框图如图⑷所示，该程序运行后，输出的x 值为31，则a 等于 ．图⑷【解析】 ⑴ A⑵ 5；15．⑶ ① 不正确，判断框出的“是”与“否”写反了．② 5050S = ⑷1a =【备选】某次考试，满分100分，按规定x ≥80者为良好，6080<x ≤者为及格，小于60者不及格，写出算法，并画出当输入一个同学的成绩x 时，输出这个同学属于良好、及格还是不及格的程序框图． 【解析】 框图如右．1S ：输入一个同学的成绩x 2S ：若80x ≥，输出这个同学属于良好， 若80x <，执行3S 3S ：若6080x <≤，输出这个同学属于及格， 若60x <，执行4S 4S ：输出这个同学属于不及格 5S ：结束1011． 随机抽样：满足每个个体被抽到的机会是均等的抽样，共有三种经常采用的随机抽样方法：⑴简单随机抽样：从元素个数为N 的总体中不放回地抽取容量为n 的样本，如果每一次抽取时总体中的各个个体有相同的可能性被抽到，这种抽样方法叫做简单随机抽样．抽出办法：①抽签法：用纸片或小球分别标号后抽签的方法．②随机数表法：随机数表是使用计算器或计算机的应用程序生成随机数的功能生成的一张数表．表中每一位置出现各个数字的可能性相同．随机数表法是对样本进行编号后，按照一定的规律从随机数表中读数，并取出相应的样本的方法．简单随机抽样是最简单、最基本的抽样方法．⑵系统抽样：将总体分成均衡的若干部分，然后按照预先制定的规则，从每一部分抽取一个个体，得到所需要的样本的抽样方法．抽出办法：从元素个数为N 的总体中抽取容量为n 的样本，如果总体容量能被样本容量整除，设Nk n =，先对总体进行编号，号码从1到N ，再从数字1到k 中随机抽取一个数s 作为起始数，然后顺次抽取第2(1)s k s k s n k +++-，，，个数，这样就得到容量为n 的样本．如果总体容量不能被样本容量整除，可随机地从总体中剔除余数，然后再按系统抽样方法进行抽样．系统抽样适用于大规模的抽样调查，由于抽样间隔相等，又被称为等距抽样．⑶分层抽样：当总体有明显差别的几部分组成时，要反映总体情况，常采用分层抽样，使总体中各个个体按某种特征分成若干个互不重叠的几部分，每一部分叫做层，在各层中按层在总体中所占比例进行简单随机抽样，这种抽样方法叫做分层抽样．分层抽样的样本具有较强的代表性，而且各层抽样时，可灵活选用不同的抽样方法，应用广泛．例：⑴有20位同学，编号从1至20，现在从中抽取4人作问卷调查，用系统抽样方法确定所抽的编号为（ ）A ．5，8，11，14B ．2，6，10，14C ．2，4，6，8D ．5，10，15，20⑵ 某单位有职工100人，不到35岁的有45人，35到49岁的有25人，剩下的为50岁以上的人，用分层抽样抽取一个容量为20的样本，35到49年龄段抽取的人数是_______人．【解析】 ⑴D⑵ 5；【教师备案】本板块一共有4道例题，不建议老师把本板块全都复习完再做例题，老师可以先以上边的例给学生复习统计，然后让学生做例2．2．概率的古典定义：随机事件A 的概率定义为()P A =A 事件包含的基本事件数试验的基本事件总数．例：⑴某种彩票中奖概率为0.1%，某人连续买1000张彩票，下列说法正确的是（ ）A ．此人一定会中奖B ．此人一定不会中奖C ．每张彩票中奖的可能性都相等D ．最后买的几张彩票中奖的可能性大些 ⑵给出下列四种说法：①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件； ②“当x 为某一实数时可使20x <”是不可能事件；③“从100个灯泡中取出5个，5个都是次品”是随机事件；④从装有8个红球，6个白球的袋中任取2球，事件“至少有一个白球”和“都是红球”是两个对立知识点睛15.2概率与统计102事件．其中不正确的说法的个数是（ ）A ．0B ．1C ．2D ．3⑶投两颗均匀的大小相同的骰子“点数和为9”的概率是_______． 【解析】 ⑴C⑵A ⑶19【教师备案】做完统计的题后，老师就可以以上边的例给学生复习事件与古典概型，然后让学生做例3．3．几何概型事件A 理解为区域Ω的某一子区域A ，A 的概率只与子区域A 的几何度量（长度、面积或体积）成正比，而与A 的位置和形状无关，满足此条件的试验称为几何概型． 事件A 的概率定义为()AP A μμΩ=，其中μΩ表示区域Ω的几何度量，A μ表示区域A 的几何度量．例：任意取一实数([02π])x x ∈，，则1sin 2x >的概率为（ ） A ．14 B ．13C ．12D ．23【解析】 B【教师备案】做完事件与古典概型的题后，老师就可以以上边的例给学生复习几何概型，然后让学生做例4，最后再做一个概率与统计综合的题（例5）．【例2】统计⑴ 一企业生产不同型号的水泥19500袋，它们来自甲、乙、丙3条不同的生产线，为检查这 批水泥的质量，决定采用分层抽样的方法进行检测，已知甲，乙，丙三条生产线抽取的个 体数组成一个等差数列，则乙生产线生产了____________袋水泥． ⑵（2010北京理11文13） 从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图），由图中数据可知________a =．若要从身高在[)120130,，[)130140,，[]140150,三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[]140150,内的学生中选取的人数应为________．⑶ 甲乙两名运动员在某项测试中的8次成绩如茎叶图所示，1x ，2x 分别表示甲乙两名运动员这项测试成绩的平均数，1s ，2s 分别表示甲乙两名运动员这项测试成绩的标准差，则有（ ）A ．12>x x ，12<s sB ．12=x x ，12<s sC ．12=x x ，12=s sD ．12=x x ，12>s s【解析】 ⑴1950065003=经典精讲乙甲8722175531565432098103⑵ 0.030；3 ⑶ B【例3】 事件与古典概型⑴从装有2个红球和2个白球的口袋中任取两球，那么下列事件组中互斥事件的个数是（ ） ①至少有1个白球，都是白球； ②至少有1个白球，至少有1个红球； ③恰有1个白球，恰有2个白球； ④至少有1个白球，都是红球． A ．0 B ．1 C ．2 D ．3⑵某射手射击一次，击中10环、9环、8环的概率分别是0.24、0.28、0.19，则这名射手在一次射击中，击中的环数不够9环的概率是（ ）A ．0.29B ．0.71C ．0.52D ．0.48⑶在一次学生联欢会上，参加会的女同学比男同学多12人，从这些同学中随机挑选一人表演节目，若选到男同学的概率为920，则参加联欢会同学的人数为（ ）A ．54B ．66C ．108D ．120⑷已知关于x 的一元二次函数2()41()f x a x b x a b =-+∈R ，．设集合{}124P =，，，{}112Q =-，，，分别从集合P 和Q 中随机取一个数作为函数()f x 中的a 和b ，求函数()y f x =有且只有一个零点的概率．【解析】 ⑴C ；⑵D ⑶D ⑷概率为29． 【备选】双安商场举行购物抽奖促销活动，规定抽奖一次的规则为：每位顾客从装有编号为0123，，，四个相同小球的抽奖箱中，每次取出一球记下编号后再放回，连续取两次，若取出的两个小球号码相加之和等于6则中一等奖，等于5中二等奖，等于4或3中三等奖．其余情况规定为不中奖．⑴写出抽奖一次所有基本事件的全集；⑵求抽奖一次中奖的概率．【解析】 ⑴所有基本事件()()()()()()()(){0001020311101213Ω=，，，，，，，，，，，，，，，，()()()()()()()()}2220212333303132，，，，，，，，，，，，，，，⑵中奖的概率为58．【铺垫】⑴ 两根相距10米的木杆上系一根绳子，并在绳子上挂一盏灯，则灯与两端距离都大于2米的概率为__________．⑵ 一个游戏转盘上有四种颜色：红、黄、蓝、黑，并且它们所占面积的比为6:2:1:4，则指针停在红色或蓝色区域的概率为（ ）A ．413B ．613C ．713D ．1013 【解析】 ⑴ 35⑵ C【例4】 几何概型⑴已知x 是[]1010-，上的一个随机数，则使x 满足26160+-x x ≤的概率为_______． ⑵已知关于x 的一元二次函数2()41()f x ax bx a b =-+∈R ，．设点()a b ，是随机取自平面区域10424000x y x y +-⎧⎪>⎨⎪>⎩≤内的点，求函数()y f x =在区间(]1-∞，上是减函数的概率． ⑶已知直线y x b =+，[]0,4b ∈，则原点O）A ．12 B ．13 C ．14 D ．18⑷在正方体1111ABCD A B C D -表面随机取一点P （异于点1B ），则 点P 满足11PB AA ⊥的概率是________．【解析】 ⑴ 12；⑵概率为12．⑶ A⑷16【例5】概率与统计为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行抽样检查，测得身高情况的统计图如下：女生男生/cm/cm⑴ 估计该校男生的人数；⑵ 估计该校男生身高在170~185cm 之间的概率；【追问】估计该校学生身高在170~185cm 之间的概率；⑶ 从样本中身高在180~190cm 之间的男生中任选2人，求至少有1人身高在185~190cm 之间的概率．【解析】 ⑴ 全校男生大致为400人⑵3140． 【追问】12⑶至少1人在185~190之间的概率：35．【备选】一个袋中装有4个形状大小完全相同的小球，球的编号分别为1，2，3，4．⑴ 从袋中随机取两个球，求取出的球的编号之和等于5的概率．⑵ 先从袋中随机取一个球，该球的编号为m ，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n ，求2n m <+的概率．105【解析】 ⑴2163P ==． ⑵1316P =．1．平面直角坐标系中的基本公式：数轴上：21(,)d A B x x =-，其中12,x x 为数轴上的点,A B 的坐标；平面直角坐标系中：(,)d A B 1122(,)(,)A x y B x y ，． 2．直线的基本概念：直线的倾斜角α、斜率2121tan y y k x x α-==-、直线在x 轴和y 轴上的截距、直线的方程；例：⑴已知点()12P ，，()13Q -，，则直线PQ 的斜率是（ ） A ．2- B ．12 C ．12- D ．2 ⑵已知两点()23P -，、()32Q ，，直线20ax y ++=与线段PQ 相交，求a 的取值范围． 【解析】 ⑴C⑵4132a -≤≤．3．直线的方程：点斜式方程：00()y y k x x -=-； 斜截式方程：y kx b =+；两点式方程：11122121()y y x x x x y y x x --=≠--；截距式方程：1(0,0)x ya b a b+=≠≠；一般式方程：0(Ax By C A B ++=,不全为零)．例：⑴若直线l 通过点(10)，，且斜率是3，则直线l 的方程是________________．⑵经过两点(39)，、(11)-，的直线在x 轴上的截距为（ ）A ．32-B ．2C ．23-D ．23【解析】 ⑴330x y --=⑵A【教师备案】本板块一共有3道例题，也不建议老师把本板块全都复习完再做例题，老师可以结合直线的基本概念和直线方程中的例给学生复习直线的概念与方程，然后再让学生做例6．4．两条直线的位置关系：1111:0l A x B y C ++=，2222:0l A x B y C ++=， 相交12210A B A B ⇔-≠； 知识点睛15.3直线方程106平行12210A B A B ⇔-=且12210B C B C -≠； 重合12210A B A B ⇔-=且12210B C B C -=；垂直12120⇔+=A A B B ，在斜率12k k ，存在时121k k ⇔=-．例：⑴下列直线中，与直线320x y +-=垂直的是（ ）A ．320x y --=B ．320x y ++=C ．320x y --=D ．320x y ++= ⑵已知直线:220l x y +-=，则下列直线中，与l 平行的是（ ）A ．210x y +-=B ．210x y --=C ．210x y +-=D ．210x y --=⑶已知ABC △的三个顶点坐标为()()()102330A B C --，，，，，，则BC 边上的高所在的直线的方程为 ．【解析】 ⑴C⑵A⑶5350x y +-=5．点11()P x y ，到直线:0l Ax By C ++=的距离公式：d两平行线10Ax By C ++=与20Ax By C ++=之间的距离公式：d =例：已知()23P ，，直线l 的方程为3430x y +-=，则点P 到直线l 的距离为 【解析】 3【教师备案】在做完直线方程的题后，老师就可以结合直线的位置关系和点到直线的距离中的例给学生复习直线的位置关系和距离公式，然后再让学生做例7．例8是直线的应用，在直线方程六大考点中我们还讲了对称问题与最值问题，如果老师在讲义中讲了对称问题与最值问题，那在本讲就可以讲例8，如果老师没讲，那老师就可以跳过例8．【例6】 直线方程⑴ 已知0ab >，0ac <，则直线0ax by c ++=一定不经过第____象限．⑵ 设直线l的倾斜角是直线1y =+的倾斜角的12，且与y 轴的交点到x 轴的距离是3，则直线l 的方程是____________．⑶ 设A B ，是x 轴上的两点，点P 横坐标为2，且P A P B =，若直线PA 的方程为10x y -+=，则直线PB 的方程是__________．【解析】 ⑴ 三⑵3y =±⑶ 50x y +-=【例7】 直线的位置关系⑴ 已知过点()2A m -，，()4B m ，的直线与直线210x y +-=平行，则m =________； ⑵ 若直线830nx y ++=与直线210x ny +-=垂直，则n =________；经典精讲107 ⑶ 两点()10A ，，(3B 到直线l 的距离均等于1，则直线l 的方程为__________． 【解析】 ⑴ 8-；⑵ 0⑶20y -+-=20y --或10x +=或20x -=【例8】直线方程的应用⑴已知定点(01)A ，，点B 在直线0x y +=上运动，当线段AB 最短时，点B 的坐标是_______． ⑵直线l 经过点()32P ，且与x y ，轴正半轴交于A B ，两点，则当OAB △的面积最小时直线l 的方程是__________．⑶光线由点()32P ，射到直线:30l x y ++=上，经l 反射后过点()16Q ，， ①求反射光线所在直线的方程；【追问】求入射光线所在的直线方程．②求反射光线所在直线与坐标轴所围成的三角形的面积．【解析】 ⑴ 1122⎛⎫- ⎪⎝⎭， ⑵ 23120x y +-=⑶ ①240x y -+=【追问】210x y -+=②4【备选】已知直线1l 和2l 关于直线:2210l x y -+=对称，若1l 的方程为3210x y -+=，求2l 的方程．【解析】所求直线方程为4630x y -+=1．圆的方程标准方程：以点()C a b ，为圆心，r 为半径的圆的方程为：222()()x a y b r -+-=一般方程：220x y Dx Ey F ++++=，（2240D E F +->）例：过点()11A -，与()11B -，且圆心在直线20x y +-=上的圆的方程为（ ） A ．()()22314x y -++= B ．()()223124x y ++-=C ．()()22114x y +++=D ．()()22114x y -+-=【解析】 D2．直线与圆的位置关系如果直线到圆心的距离为d ，圆的半径为r ，那么：①若d r >，则直线与圆相离；②若d r =，直线与圆相切；③若d r <，则直线与圆相交．例：⑴ 过点(16)P -，且与圆22(3)(2)4x y ++-=相切的直线方程是____________．知识点睛15.4圆的方程108 ⑵ 过点(11)，的直线l 与圆224x y +=交于A B ，两点，若|AB l 的方程为（ ）A ．20x y +-=B ．210x y -+=C ．210x y --=D ．10x y --=【解析】 ⑴10x +=或34270x y -+=⑵ A3．圆与圆的位置关系设1O 的半径为1r ，2O 的半径为2r ，两圆的圆心距为d ，当12d r r >+时，两圆外离；当12d r r =+时，两圆外切； 当1212r r d r r -<<+时，两圆相交； 当12d r r =-时，两圆内切； 当12d r r <-时，两圆内含．【教师备案】本板块主要是圆的方程，因为在讲义中只有圆的初步一讲，圆涉及到的知识比较简单，所以老师可以一块给学生复习，复习完知识点后就可以让学生做例9，同样，如果老师在前边的讲义中没有讲圆的初步一讲，那老师可以不讲本板块．【例9】 圆的方程⑴由直线1y x =+上的点向圆22(3)(2)1x y -++=引切线，则切线长的最小值为（ ）A． BCD．⑵已知圆C 方程为()2215x y +-=，直线l 方程为：10mx y m -+-=．①求证：对m ∈R ，直线l 与圆C 总有两个不同交点；②若直线l 与圆C 交于A ，B两点，且AB =，求m 的值．【解析】 ⑴B⑵①当0m =时，直线l 为1y =，由题意可知直线l 与圆C 相交；当0m ≠时，由题意可知圆心为()01，， ∴圆心到直线的距离为()01d ===，，d <∴，∴直线与圆C 相交；∴对m ∈R ，直线l 与圆C 总有两个不同交点②m =或m =．经典精讲。
高一数学补充讲义6：函数的对称性一、基本结论：（一）单个函数本身具有的对称性：已知函数()y f x =，1、轴对称（1）若()()f x f x =-，则()f x 的图象关于0x =（y 轴）对称；（2）若(1)(1)f x f x +=-，则()f x 的图象关于直线1x =轴对称；（3）若()()f a x f a x +=-，则()f x 的图象关于直线x a =轴对称；（4）若()()f a x f b x +=-，则()f x 的图象关于直线2a b x +=轴对称；2、中心对称（5）若()()f x f x =--，则()f x 的图象关于点(0,0)对称；（6）若(1+)(1)f x f x =--，则()f x 的图象关于点(1,0)对称；（7）若()()f a x f a x +=--，则()f x 的图象关于点(,0)a 对称；（8）若()()2f a x f a x b ++-=，即()2()f a x b f a x +=--，则()f x 的图象关于点(,)a b 对称；对称性的证明例题：（1）求证：2()(1)f x x =-关于1x =对称；（2）求证：3()(1)2f x x =-+关于点(1,2)对称；（二）两个函数间的对称性：已知函数()y f x =，1、轴对称（1）函数()y f x =与函数()y f x =-关于直线0x =（y 轴）对称；（2）函数()y f x =与函数()y f x =-关于直线0y =（x 轴）对称；（3）函数(1)y f x =+与函数(1)y f x =-关于直线0x =（y 轴）对称；（4）函数()y f a x =+与函数()y f a x =-关于直线0x =（y 轴）对称；（5）函数()y f a x =+与函数()y f b x =-关于直线2b a x -=对称； （6）函数()y f x =与函数1()y fx -=关于直线y x =对称；（其中1()y f x -=为函数()y f x =的反函数）。
数学学科高一春季讲义一、本节知识【例1】 已知函数15()sin(2)264f x x π=++，（1）求()f x 的最小正周期及单调区间； （2）求()f x 的图像的对称轴和对称中心； （3）求()f x 的最值及取得最值时的x .【变式1】函数)22sin(π+=x y 的图像的一条对称轴方程是（ ）A.π45=x B.2π-=x C.8π=x D.4π=x 【变式2】函数()cos(3),f x x x R ϕ=+∈的图象关于原点中心对称，则ϕ=（ ） A.3πB.2k ππ+，k Z ∈C.,k k Z π∈D.2,2k k Z ππ-∈【变式3】给出下列命题：①函数5sin(2)2y x π=-是偶函数;②方程8x π=是函数5sin(2)4y x π=+的图象的一条对称轴方程; ③若α、β是第一象限角，且αβ>，则sin sin αβ>. 其中正确命题的序号是 .（填序号）【例2】求函数tan(3)4y x π=-的定义域、周期、单调区间。
【例3】函数3sin(3),[,]622y x x πππ=-∈-的单调递增区间是_________.【例4】函数1y x =-的值域为_______________. 【变式】若函数cos y a b x =-的最大值是32，最小值是12-，求函数4sin y a bx =-的最大值与最小值。
【例5】函数21,2y sinx sin x x R =+∈的值域是___________________. 【变式1】函数2()cos sin f x x x =+在区间[,]44ππ-上的值域是___________________. 【变式2】求函数),2.(1tan tan 2z k k x R x x x y ∈+≠∈++=ππ的值域。
【例6】函数sin 2sin y x x =-的值域为（ ） A. []3,1-- B. []1,3- C. []0,3 D. []3,0- 【例7】函数2sin 1sin 1x y x +=-的值域为_______________.【例8】下列函数中，不是奇函数的是（ ） A ．sin tan y x x =+ B ．tan 1y x x =- C ．sin tan 1cos x x y x -=+ D ．1tan lg 1tan xy x-=+【例9】设()f x 是定义在R 上且最小正周期为32π的函数，在某一周期内，cos2,0,()2sin ,0,x x f x x x ππ≤≤⎧-<⎪=⎨⎪<⎩ 则154f π⎛⎫- ⎪⎝⎭= .【变式】定义在R 上的函数()f x 既是偶函数又是周期函数，若()f x 的最小正周期是π，且当[0,]2x π∈时，()sin f x x =，则5()3f π的值为（ ）A. 12-B.C. D.12【例10】若函数()2cos(2)f x x ϕ=+对任意实数x 都有()()66f x f x ππ-=+．（1）求()6f π的值；（2）求ϕ的最小正值；（3）当ϕ取最小正值时，求()f x 在,63ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值．【例11】已知函数π()sin()(0,0,||)2f x A x A ωϕωϕ=+>><的图象在y 轴上的截距为1，它在y 轴右侧的第一个最大值点和最小值点分别为0(,2)x 和0(3π,2)x +-. （1）求()f x 的解析式；（2）用列表作图的方法画出函数()y f x =在长度为一个周期的闭区间上的图象.【例12】已知函数()sin ()3f x A x πϕ=+，x R ∈，0A >，02πϕ<<.()y f x =的部分图像如图所示，P 、Q 分别为该图像的最高点和最低点，点P 的坐标为(1,)A . （1）求()f x 的最小正周期及ϕ的值； （2）若点R 的坐标为(1,0)，23PRQ π∠=，求A 的值.【知识点二】1、函数x y sin =的图像变换得到)sin(ϕω+=x A y 的图像的步骤：2、图像变换①左右平移变换：()0>a )()(a x f y x f y +=−→−=； )()(a x f y x f y -=−→−= ②上下平移变换：()0>h h x f y x f y +=−→−=)()(； h x f y x f y -=−→−=)()( ③伸缩变换：()0>ω)()(x f y x f y ω=−→−=； ()0>A )()(x Af y x f y =−→−= ④对称变换：)()(x f y x f y -=−→−=； )()(x f y x f y -=−→−=； )()(x f y x f y --=−→−=⑤翻折变换：)()(x f y x f y =−→−=； )()(x f y x f y =−→−=【例1】下列函数中，既是区间02(,)π上的增函数，又是以π为周期的偶函数的是（ ）A ．y xtan x =B ．y |sin x|=C ．2y cos x =D ．y sin|x |= 【变式1】函数1|sin(3)|2y x =+的最小正周期是（ ） A ．2π B ．πC ．2πD ．4π【变式2】函数sin y x =的一个单调增区间是（ ） A.,44ππ⎛⎫- ⎪⎝⎭B.3,44ππ⎛⎫ ⎪⎝⎭C.3,2ππ⎛⎫ ⎪⎝⎭D.3,22ππ⎛⎫ ⎪⎝⎭【例2】把函数sin(2)4y x π=+的图像向左平移8π个单位长度，再将横坐标压缩到原来的12，所得函数的解析式为（ ） A ．sin 4y x = B ．cos4y x =C ．sin(4)8y x π=+D ．sin(4)32y x π=+【变式】为了得到函数πsin 23y x ⎛⎫=- ⎪⎝⎭的图像，只需把函数πsin 26y x ⎛⎫=+ ⎪⎝⎭的图像（ ）A ．向左平移π4个长度单位B ．向右平移π4个长度单位C ．向左平移π2个长度单位 D ．向右平移π2个长度单位 【例3】要得到cos(2)4y x π=-的图像，只需将sin 2y x =的图像（ ）A ．向左平移8π个单位 B ．向右平移8π个单位 C ．向左平移4π个单位D ．向右平移4π个单位【变式】要得到函数y x =的图象，只需将函数)4y x π=+的图象上所有的点的（ ）A ．横坐标缩短到原来的12倍（纵坐标不变）,再向左平行移动8π个单位长度 B ．横坐标缩短到原来的12倍（纵坐标不变）,再向左平行移动4π个单位长度 C ．横坐标伸长到原来的2倍（纵坐标不变）,再向左平行移动4π个单位长度 D ．横坐标伸长到原来的2倍（纵坐标不变）,再向左平行移动8π个单位长度【例4】已知函数()sin()f x A x ωϕ=+（0A >，0ω>，2πϕ<）的图象在y 轴上的截距为1，它在y 轴右侧的第一个最大值点和最小值点分别为()0,2x 和()03,2x π+-．（1）求()f x 的解析式；（2）将()y f x =图象上所有点的横坐标缩短到原来的13，（纵坐标不变），然后再将所得图象沿x 轴正方向平移3π个单位，得到函数()y g x =的图象．写出函数()y g x =的解析式并用“五点法”画出()y g x =在长度为一个周期的闭区间上的图象．【例5】已知函数()sin (,)4f x a x a b Z π⎛⎫=++∈ ⎪⎝⎭的图像过（0，1），且当0,2x π⎡⎤∈⎢⎥⎣⎦时，()f x的最大值为1．（1）求()f x 的解析式；（2）由()f x 的图象是否可以经过平移变换得到一个奇函数()y g x =的图象？若能，请写出变换过程；若不能，请说明理由．二、课堂检测1、设函数()sin(2)3f x x π=+，则下列结论正确的是（ ）A ．()f x 的图象关于直线3x π=对称 B ．()f x 的图象关于点(,0)4π对称C ．把()f x 的图象向左平移12π个单位，得到一个偶函数的图象 D ．()f x 的最小正周期为π，且在[0,]6π上为增函数2（1（2）要得到函数g (x )f (x ) （3）y ＝f (x )（4）y ＝f (x )在[0，2π] 其中正确命题的序号为________．3、设函数()sin(2),(0)f x x ϕπϕ=+-<<，()y f x =图像的一条对称轴是直线8x π=（1）求ϕ；（2）求函数()y f x =的单调增区间。
当前形势解不等式在近五年北京卷（理）考查5～10分高考 要求内容要求层次 具体要求A B C 含参不等式解法√运用不等式的性质熟练解决含参不等式以及恒成立问题解不等式的其它方法√理解二次函数、二次方程与二次函数图象之间的关系，并会从函数的角度解决不等式问题，考虑单调性和图象法．北京 高考 解读2009年 2010年（新课标）2012年（新课标） 2013年（新课标）第13题5分第1题5分 第7题5分第14题5分第8题5分<教师备案> 不等式的解法是高考中的必考内容，由于教学要求的变化，考查要求有所降低，直接考查主要以选择题，填空题为主，题目小巧灵活新颖；主要以导数解答题的形式出现，考查含参数不等式的解法．间接解法考查更多，往往与函数，导数，数列等内容结合，以求取值范围的设问方式呈现，有一定的难度和综合性．知识切片新课标剖析满分晋级第6讲常见不等式 通用解法不等式1级 不等式初步不等式2级 常见不等式通用解法不等式3级 均值不等式三大难点突破<教师备案> 在寒假班的时候解不等式部分我们重点讲了变形后转化为一元二次不等式，已知解的结构进而处理系数问题．我们在这里简单回顾一下．1、 解不等式：①2260x x --<； ②2210x x -->； ③1392x x +->；④()()222log 43log 211x x x +->-+．【解析】 ①不等式的解集为322⎛⎫- ⎪⎝⎭，．②不等式的解集为(()112-∞++∞，，③()30,log 2x ∈．④不等式解集为1,22⎛⎫⎪⎝⎭．2、 已知关于x 的不等式20x ax b -+<的解集为(14)，，求2a b +的值． 【解析】 214a b +=．3、 当不等式2230x px ++≤恰好只有一实数解时，实数p 的值为________．【解析】 ±4、 关于x 的不等式2432x ax>+的解集是非空集合()()22,m -，则am 的值等于_____．【解析】 386.1含参一元二次不等式寒假知识回顾考点1：解含参不等式对于含有参数的一元二次不等式，解法步骤总结如下： ①首先应判定二次项系数是否为零，分别加以讨论；②在二次项系数不为零的条件下，将二次项系数化为正的，讨论对应的二次方程是否有根，即讨论判别式的正负；③在有根的情况下进行因式分解或利用求根公式求出二次方程对应的根； ④比较两根的大小，分别得到参数的范围，写出解集． ⑤最后将可以合并的合并，并按参数的范围分别写出解集．<教师备案>含参数的一元二次不等式的解答是以后要学习的求导数的单调性的基础，在高考中是必考的，需要对参数进行各种分类讨论，不重不漏，遵循一定的原则，养成良好的分类习惯．【例1】 ⑴求关于x 的不等式210x ax ++>的解集．⑵求关于x 的不等式2(2)20x a x a -++>的解集． ⑶求关于x 的不等式22(1)40ax a x -++>的解集．【解析】 ⑴不等式的解集为a a ⎛⎛⎫-+-∞+∞⎪ ⎪⎝⎭⎝⎭． ⑵ 当2a >时，不等式的解集为： ()()2a -∞+∞，，； 当2a =时，不等式的解集为： (2)(2)-∞+∞，，； 当2a <时，不等式的解集为： ()()2a -∞+∞，，．⑶ 综上知：当0a =时，不等式的解集为(2)-∞，；当0a <时，不等式的解集为22a ⎛⎫⎪⎝⎭，；当01a <<时，不等式的解集为2(2)a ⎛⎫-∞+∞ ⎪⎝⎭，，；当1a =时，不等式的解集为(2)(2)-∞+∞，，； 当1a >时，不等式的解集为2(2)a ⎛⎫-∞+∞ ⎪⎝⎭，，．考点2：已知一元二次不等式解集求参数范围此类题型一般有两种处理方法：⑴ 由一元二次不等式的解集的形式考虑对应的二次函数的图象，把解集转换为二次函数的图象与x 轴的交点问题，进而转化为对应的关于参数的不等式，从而解出参数的范围．⑵ 我们把含参数的不等式看成一个含有两个变量的不等式．若通过整理，可以将这个不等式中的两个变量分别调整到不等号的两端，使之每一边仅含有一个变量，这个方法通常叫做分离参数．对于一个含参不等式，如果我们可以对它分离参数，那么我们不论知道哪一个变量的取值范围，去求另一个的范围都很容易了，因为我们要研究的都只是一个含有一个自变量的函数的值域问题． 此类问题的一部分具体处理方式我们在本讲第三板块讲解，全面的类型在高二导数部分和高三复习知识点睛经典精讲的时候会重点讲解．【例2】 ⑴已知1230a a a >>>，则使得2(1)1i a x -<(123)i =，，都成立的x 取值范围是（ ）A ．110a ⎛⎫ ⎪⎝⎭，B ．120a ⎛⎫ ⎪⎝⎭，C ．310a ⎛⎫ ⎪⎝⎭，D ．320a ⎛⎫ ⎪⎝⎭，⑵关于x 的不等式组()222022550x x x k x k ⎧-->⎪⎨+++<⎪⎩的解集中的整数恰好只有一个，则实数k 的取值范围为________．【解析】 ⑴ B⑵ [)(]3,23,4-【铺垫】要使满足关于x 的不等式2290x x a -+<（解集非空）的每一个x 至少满足不等式2430x x -+<和2680x x -+<中的一个，则实数a 的取值范围是 ． 【解析】 8178⎡⎫⎪⎢⎣⎭，；【例3】设不等式2220x ax a -++≤的解集为M ，如果[14]M ⊆，，求实数a 的取值范围．【追问】若将本题改为：若[14]M ⊆，，求a 的取值范围，【解析】a 的取值范围是1817⎛⎤- ⎥⎝⎦，． 【追问】a 的取值范围为[3,)+∞．考点3：解分式不等式1．对于含有分式的不等式解法思路：先将不等式整理为()()0f x g x >或()()0f x g x ≥，再化为整式不等式求解． ()()()()00f x f x g x g x >⇔>；()()()()()000f x g x f x g x g x ⎧⎪⇔⎨≠⎪⎩≥≥ 2．数轴标根法使用范围：对于能分解成一些一次因式的乘积或一次因式的商的不等式． 注意事项：每个一次因式中x 的系数都为正；对于高次因式先约去其次数．<教师备案>分式不等式以及很多非常规不等式，主要思路一般都是将不等式转化为整式不等式，然后经典精讲知识点睛6.2分式不等式、绝对值不等式与无理不等式进行因式分解或由求根公式，利用标根法得出解集．需要注意的是，转化时要等价，比如分母不能为0，根号下的式子要非负等等．标根法可以简单的举几个例子，比如求()()()()12340x x x x --++>的解集．【例4】 ⑴关于x 的不等式724x x x -+≥的解集为___________．⑵若10a +>，则不等式221x x ax x ---≥的解集为________．⑶已知不等式20ax bx c ++>的解集是{}|x x αβ<<，其中1βα>>，则不等式 ()220a ax bx c cx bx a++<++的解集是 ．【解析】 ⑴ 不等式的解集为()[],41,2-∞-．⑵ (](1)a -∞-+∞，， ⑶ 不等式的解集为11|x x x x βααβ⎧⎫><<<⎨⎬⎩⎭或或．【备选】求关于x 的不等式(1)1(1)2a x a x ->≠-的解集．【解析】 综上所述可知：当0a <时，原不等式的解集为221a a -⎛⎫⎪-⎝⎭，； 当0a =时，原不等式的解集为∅；当01a <<时，原不等式的解集为221a a -⎛⎫ ⎪-⎝⎭，；当1a >时，原不等式的解集为2(2)1a a -⎛⎫-∞+∞ ⎪-⎝⎭，，．考点4：解绝对值不等式对于含有绝对值的不等式，解题的思想如下：1．化去绝对值符号，转化为不含绝对值的不等式： ①()()()0f x a a a f x a <>⇔-<<； ②()()()0f x a a f x a >>⇔<-或()f x a >； ③()()()()()f x g x g x f x g x <⇔-<<； ④()()()()f x g x f x g x >⇔<-或()()f x g x >．2．构造绝对值函数，通过函数图象的位置关系转化，利用数形结合找到解集的形式，进而转化为方程去解出解集区间的端点．3．用零点分段去绝对值符号来求解．此时需要注意： 经典精讲知识点睛①区间端点处的值不能遗漏；②在各个区间上解出的结果应与本区间求交集； ③各区间上的解集并起来，才得原不等式的解集．<教师备案>解含绝对值符号的不等式，关键是去绝对值，可以分段讨论，可以平方，也可以用图象来处理，或者用绝对值的几何意义，总之就是将含绝对值不等式等价转化，但尽量不要让问题复杂化．【例5】 ⑴解下列不等式：①()()110x x +->；②2341x x x --<+；⑵若不等式34x b -<的解集中的整数有且仅有123，，，则b 的取值范围为 ． ⑶解关于x 的不等式：21x ax -<．【解析】 ⑴ ①不等式的解集为{}11x x x <≠-且．②原不等式解集为()3,5． ⑵ (57)，⑶ 综上所述：当0a <时，原不等式解集为⎝⎭；当0a =时，原不等式解集为∅；当0a >时，原不等式解集为⎛ ⎝⎭．【备选】若不等式43x x a -+-<的解集是空集，求实数a 的取值范围．【解析】1a ≤． <教师备案>对于形如x a x b m -+->或x a x b m -+-<（0m >为常数）的不等式，利用实数绝对值的几何意义，数形结合求解较简便．考点5：解无理不等式无理不等式往往需要转化为有理不等式组进行求解．常见类型及解法如下：()()()00g x g x f x ⎧<⎪>⇔⎨⎪⎩≥或()()()20g x f x g x ⎧⎪⎨>⎡⎤⎪⎣⎦⎩≥；()()()()()200f x g x g x f x g x ⎧⎪⎪⇔>⎨⎪<⎡⎤⎪⎣⎦⎩≥．<教师备案>重点是将无理不等式等价转化，需要注意的是根号下的式子要非负．知识点睛经典精讲【例6】 ⑴2x+； ⑵2x -； ⑶()x a a >-∈R ．【解析】 ⑴ 不等式的解集为[)1,+∞．⑵ 不等式解集为1,52⎡⎫⎪⎢⎣⎭．⑶ 综上所述，当0a <时，原不等式解集为(),0a ；当0a =时，原不等式解集为∅；当0a >时，原不等式解集为[),a a -．<教师备案>解决含有参数的不等式恒成立问题，一般都可以转化为一元二次不等式相关的问题，其处理方法大致有两种： ①整体分析法：将不等式问题转化为含参的一元二次函数的零点分布问题，再利用根的判别式或数形结合的思想，得到相关不等式，使问题得到解决； ②参数分离法：将参数分离出来，将恒成立问题转化为求函数最大值或最小值的问题．一般参数容易分离时，第②个方法比较容易；当参数不容易分离或分离后得到的函数太复杂时，再考虑用整体分析法，通过数形结合与分类讨论得到结果．还有一种不是很常用的方法，不等式含有两个变量时，可以灵活的将代数式看成其中任一个变量的函数，复杂程度往往有很大的区别．【例7】 ⑴已知210ax ax ++≥在R 上恒成立，则实数a 的取值范围是 ．⑵若不等式210x ax ++≥对于一切102x ⎛⎤∈ ⎥⎝⎦，恒成立，则a 的最小值是（ ）A ．0B ．2-C ．52- D ．3-【追问】若当[]3,2x ∈--时恒成立，则a 的取值范围为___________．⑶若[]13a ∈，，使得不等式2(2)20ax a x +-->恒成立，则实数x 的取值范围是_________．【解析】 ⑴ 04a ≤≤⑵ C【追问】52a ≤．⑶ 2x >或1x <-【挑战8分钟】① 已知220x ax a --<在()21--，上恒成立，求实数a 的取值范围．经典精讲经典精讲6.3恒成立问题② 若(]1x ∈-∞-，，()21390x x a a ++->恒成立，求实数a 的取值范围．【解析】 ① 解得43a -≤． ② 34a -<<．【备选】已知二次函数2()f x ax x =+，如果[0,1]x ∈时|()|1f x ≤，求实数a 的取值范围． 【解析】 20a -<≤． 【点评】 [0,1]x ∈时，()1f x ≤⇔max ()1f x ≤且min ()1f x ≤．max ()max (0)(1)f x f f =，，于是有(0)1f ≤且(1)1f ≤，解得20a -≤≤；min ()f x 需要讨论对称轴12x a=-是否在区间[01]，上，得到一些不等式，解得结果． 这是一种整体考虑的思想，解析中是参数分离的思想．设函数2()1f x x =-，对任意32x ⎡⎫∈+∞⎪⎢⎣⎭，，24()(1)4()x f m f x f x f m m ⎛⎫--+ ⎪⎝⎭≤恒成立，则实数m 的取值范围是 ． 【解析】3⎛⎡⎫-∞-+∞ ⎪⎢ ⎪⎝⎦⎣⎭，，．【演练1】已知集合{}12M x x x =-∈R ≤，，511P xx x ⎧⎫=∈⎨⎬+⎩⎭Z ≥，，则M P ∩等于（ ） A ．{}03x x x <∈Z ≤， B ．{}3x x x ∈Z 0≤≤，C ．{}1x x x -∈Z ≤≤0，D ．{}10x x x -<∈Z ≤，【解析】 B【演练2】在R 上定义运算⊗：(1)x y x y ⊗=-．若不等式()()1x a x a -⊗+<对任意实数x 成立，则（ ）A ．11a -<<B ．02a <<C ．1322a -<<D ．3122a -<<【解析】 C【演练3】当()12x ∈，时，不等式240x mx ++<恒成立，则m 的取值范围是 ． 【解析】 5m -≤【演练4】设m ∈R ，求关于x 的不等式22230m x mx +-<的解集． 【解析】 ∴当0m =时，原不等式的解集为R ；当0m >时，原不等式的解集为31m m ⎛⎫- ⎪⎝⎭，；实战演练当0m <时，原不等式的解集为13mm ⎛⎫- ⎪⎝⎭，．【演练5】（2010山东省聊城一中高三模拟）已知关于x 的不等式22221463x kx kx x ++<++的解集为R ，而关于x 的不等式2(2)0kx k x k --+≤的解集为∅，求实数k 的取值范围．【解析】 k 的取值范围为13k <<．（全国高中数学联赛江苏赛区初赛13）+对于任意正实数x ，y 成立，求k 的取值范围．【解析】 显然0k >．∴2222(2)(21)(1)0k x y k x k y +⇒--+-≤≥对于x ，0y >恒成立．令0t =，则得222()(21)2(1)0f t k t t k =--+-≥对一切0t >恒成立． 当2210k -≤时，不等式不可能恒成立，故2210k ->．此时当2121t k =-时，()f t 取得最小值4222222221223(23)121212121k k k k k k k k k ---+-==----． 当2210k ->且2230k -≥，即k且当232k =时，即12t =，40x y =>时，等号成立．∴k ⎫∈+∞⎪⎪⎣⎭．大千世界。
