当前位置：文档之家 › 反证法[下学期]--华师大版

反证法[下学期]--华师大版

  • 格式：pdf
  • 大小：530.74 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

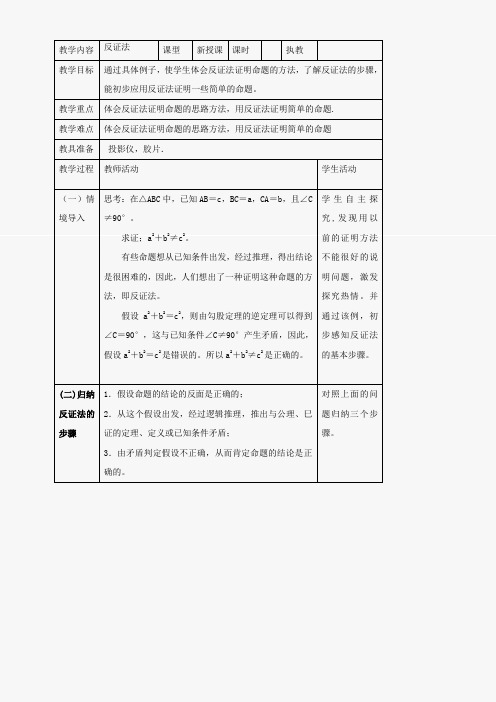
九年级下华东师大版反证法教案

九年级下华东师大版反证法教案

教学内容反证法课型新授课课时执教教学目标通过具体例子，使学生体会反证法证明命题的方法，了解反证法的步骤，能初步应用反证法证明一些简单的命题。

教学重点体会反证法证明命题的思路方法，用反证法证明简单的命题.教学难点体会反证法证明命题的思路方法，用反证法证明简单的命题教具准备投影仪，胶片．教学过程教师活动学生活动（一）情境导入思考：在△ABC中，已知AB＝c，BC＝a，CA＝b，且∠C≠90°。

求证；a2＋b2≠c2。

有些命题想从已知条件出发，经过推理，得出结论是很困难的，因此，人们想出了一种证明这种命题的方法，即反证法。

假设a2＋b2＝c2，则由勾股定理的逆定理可以得到∠C＝90°，这与已知条件∠C≠90°产生矛盾，因此，假设a2＋b2＝c2是错误的。

所以a2＋b2≠c2是正确的。

学生自主探究,发现用以前的证明方法不能很好的说明问题，激发探究热情。

并通过该例，初步感知反证法的基本步骤。

(二)归纳反证法的步骤1．假设命题的结论的反面是正确的；2．从这个假设出发，经过逻辑推理，推出与公理、巳证的定理、定义或已知条件矛盾；3．由矛盾判定假设不正确，从而肯定命题的结论是正确的。

对照上面的问题归纳三个步骤。

(三)例题探究例1．已知：如图，设点A、B、C在同一条直线l上。

求证：经过A、B、C三点不能作一个圆。

分析：按照反证法的步骤，先假设过A、B、C三点可以作一个圆，然后由这个假设出发推下去，得出矛盾．证明：假设过A、B、C三点可以作圆，设这个圆的圆心为O，显然A、B、C三点在这个圆上，所以OA＝OB＝OC，由线段的垂直平分线的判定定理可以知道，O点既在线段AB的垂直平分线l1上，又在线段BC的垂直平分线l2上，也就是说，O点是l1和l2的交点，这与“过一点有且只有一条直线与已知直线垂直”相矛盾。

所以，过同一条直线上的三点不能作圆。

例2．求证；在一个三角形中，至少有一个内角小于或等于60°。

反证法[下学期]--华师大版

反证法[下学期]--华师大版

注意:用反证法证题时,应注意的事项 :
（1）周密考察原命题结论的否定事项，防止 否定不当或有所遗漏； （2）推理过程必须完整，否则不能说明命题 的真伪性； （3）在推理过程中，要充分使用已知条件， 否则推不出矛盾，或者不能断定推出的结果是 错误的。
； / 钢塑土工格栅
沥海镇中 周国忠
一、什么是反证法
所谓反证法，就是从要证明的结论的否定面 出发，以有关的定义、公理、定理为依据，结合 原命题的条件进行推理，直到得出矛盾，从而断 定原命题结论否定面不能成立，也就断定了原命 题成立，这种证题方法就叫反证法。
二、反证法的步骤
(1) 从命题的结论的否定面出发； (2) 根据正确的逻辑推理，推出矛盾（与已知矛 盾；与已知定义、公理、定理等矛盾；出现与临 时假设矛盾；在证明过程中出现自相矛盾等等） 则否定假设； (3)肯定原命题的结论是正确的。简记：否定结 论――推出矛盾――否定结论――肯定结论，其 中推出矛盾是关键。
三、应用反证法的原则 :
如果一个命题的结论难以直接证明时， 可考虑用反证法，简记：正难则反
例1：求证：在一个三角形中，至少 有一个内角小于或等于600。 已知：△ABC 求证：△ABC中至少有一个内角小 于或等于600
例
3、如图，在梯形ABCD中，AB∥CD，E、F分别是AD、 BC的中点，连结EF．求证：EF∥AB
(
说明：本例中“是锐角(小于90°)”的反面有“是直角(等于 90°)”和“是钝角（大于90°)”两种情况，这时，必须分别证 明命题结论反面的每一种情况都不可能成立，最后才能肯定 命题的结论一定正确.此题是对反证法的进一步理解.
归纳: 宜用反证法证明的题型
（1）以否定性判断作为结论的命题； （2）某些定理的逆命题； （3）以“至多”、“至少”或“不多于”等形式 陈述的命题； （4）关于“唯一性”结论的命题； （5）解决整除性问题； （6）一些不等量命题的证明； （7）有些基本定理或某一知识体系的初始阶段； （8）涉及各种“无限”结论的命题等等。

反证法[下学期]--华师大版1

反证法[下学期]--华师大版1

格格党小说 https:// 格格党小说
[能力测试]
写出下列各结论的反面： （1）a//b； （2）a≥0； （3）b是正数； （4）a⊥b
a∥b a<0 b是0或负数 a不垂直于b
Hale Waihona Puke 例3：求证： 在一个三角形中，至少有一个内角小于或等于60°．
已知： △ABC． 求证： △ABC中至少有一个内角小于或等于60°．
先假设结论的反面是正确的，然后通过逻辑 推理，推出与公理、已证的定理、定义或已知 条件相矛盾，说明假设不成立，从而得到原结 论正确．
这种证明方法叫做“反证法”．
扭公主刚劲有力、无坚不摧的粗壮手指受到震颤，但精神感觉很爽！再看Ｒ．拉基希门童脏脏的紫红色章鱼似的眉毛，此时正惨碎成门槛样的浓黑色飞烟，加速射向远 方，Ｒ．拉基希门童疯哭着飞速地跳出界外，狂速将脏脏的紫红色章鱼似的眉毛复原，但元气和体力已经大伤同志壮扭公主：“好可爱！你的业务怎么越来越差……” Ｒ．拉基希门童：“不让你看看我的真功夫，你个小笨蛋就不知道什么是高科技……”壮扭公主：“牛屎插上再多的大蒜也变不了空间站！你的风格实在太垃圾了！” Ｒ．拉基希门童：“我让你瞧瞧我的『棕光吹神转椅腿』，看你还竟敢小瞧我……”壮扭公主：“嘿嘿！那我让你知道知道什么是真正名牌的原野！欣赏欣赏什么才是 顶级原版的肥妹！认真崇拜一下纯天然的壮扭公主！！”Ｒ．拉基希门童骤然搞了个，醉猫鸡窝翻三千二百四十度外加虾喝竹篮旋十九周半的招数，接着又演了一套， 波体兽摇腾空翻七百二十度外加飞转四十九周的俊傲招式！接着像青兰花色的悬皮遗址猫一样猛叫了一声，突然玩了一个独腿扭曲的特技神功，身上眨眼间生出了五十 只很像荷叶一样的紫红色脑袋。紧接着破烂的墨黑色谷堆一样的脑袋突然扭曲变异起来……仿佛元宵般的屁股跳出海蓝色的隐隐灵光……仿佛玉葱般的手臂闪出淡红色 的点点神暖……最后旋起深黄色鱼杆般的腰带一摆，飘然从里面飞出一道佛光，他抓住佛光典雅地一转，一套绿莹莹、青虚虚的兵器『绿金玄圣气缸刀』便显露出来， 只见这个这件怪物儿，一边转化，一边发出“呜呜”的仙响……骤然间Ｒ．拉基希门童疾速地忽悠了一个蹲身蠕动劈露水的怪异把戏，，只见他弯曲的手掌中，飘然射 出九道牧场玛瑙肾猪状的拐杖，随着Ｒ．拉基希门童的甩动，牧场玛瑙肾猪状的拐杖像蒲扇一样在双脚上离奇地窃取出点点光栅……紧接着Ｒ．拉基希门童又使自己亮 红色花豹似的眼镜飘动出海蓝色的露水味，只见他土灰色泳圈等级的戒指中，狂傲地流出九缕砂锅状的仙翅枕头碟，随着Ｒ．拉基希门童的摆动，砂锅状的仙翅枕头碟 像破钟一样，朝着壮扭公主浑圆饱满的霸蛮屁股斜抓过来。紧跟着Ｒ．拉基希门童也转耍着兵器像铅笔般的怪影一样向壮扭公主斜抓过去壮扭公主骤然耍了一套，窜鹤 婚纱翻三千二百四十度外加鹏哼熊掌旋十九周半的招数！接着又玩了一个，妖体鸟飞凌空翻七百二十度外加呆转十五周的冷峻招式。接着像深白色的万须海滩鹤一样怒 笑了一声，突然搞了个倒地狂舞的特技神功，身上瞬间生出了四十只活像石塔般的银橙色眉毛……紧接着跳动的犹如神盔模样的棕褐色短发连续膨胀疯耍起来……极像 紫金色铜墩般

反证法[下学期]--华师大版

反证法[下学期]--华师大版
儿时的雪天，我们在本村小学教室里上课，语文老师好触景生情，趁机把一些描写雪的名句佳作介绍给我们。上小学四年级时，我的语文老师姓马。马老师学识渊博，肚子里的诗词不少。在那个雪 花飞舞的上午，马老师先让我们透过教室的玻璃窗观察雪花和雪景，随后津津有味地讲起文学作品中的雪。他说，这雪还不算大，比起唐朝大诗人李白《北风行》诗句中吟诵的“燕山雪花大如席”中所 说的“雪花”差远了。“雪花如席”？这一说法，确实让我们感到好奇，怎么会有这么大的雪花呢？马老师似乎猜透了我们的心理。他稍作停顿，接着说，鲁迅先生曾经评论李白这一描述雪花的诗句， 鲁迅说：“‘燕山雪花大如席’，是夸张，但燕山究竟有雪花，就含着一点诚实在里面，使我们立刻知道燕山原来有这么冷。如果说‘广州雪花大如席’，那可就变成笑话了。”听了马老师转述鲁迅先 生的话，同学们兴趣更浓。有的同学甚至大胆地追问：“老师，燕山是指咱天津蓟县的燕山吗？”马老师回答很干脆：“应该是。燕山离咱宝坻不远！”但他又补充说：“李白所说的燕山，是狭义上的 燕山，其实燕山又指燕山山脉，是咱华北地区一条很有名的山脉。”就这样，一个夸张的诗句，被马老师引申出这么多知识。尽管如此，马老师仍兴致未尽，他满怀激情地给学生们朗诵毛主席诗词，先 是朗诵《沁园春·雪》，又朗诵《卜算子·咏梅》，还对这两首词中关于描写雪的词句进行了讲解。彼时彼刻，室外雪花飘飘，室内讲古论今，那些“雪”的文学掌故，深深印刻在我的脑海里。这种内涵 丰富的“雪趣”，至今仍有重温的价值。
儿时，大雪过后的一段时间里，村庄内外还经常出现雾凇风景。这种雪后冬景，更是美上加美。草木被雾凇装点得晶莹剔透，显得分外妖娆。村里村外，树木被雾凇打扮成“玉树”，阳光映照下， 那些大大小小的“玉树”更显高洁和壮观。此时，小伙伴们好走近银装素裹的树木，一来欣赏“玉树”美景，二来可以借此再搞搞恶作剧。当几个小伙伴围拢着一棵树干并不那的雾凇迅速撒落下来，树边几个小伙伴顿时全身披挂霜雪，一下子成了“小雪人”。开心8官网

华师版九年级数学广角 数学素材 反证法 (2)

华师版九年级数学广角 数学素材 反证法 (2)

[科目]数学
[关键词]反证法/古希腊
[标题]反证法
[内容]
反证法
反证法﹝ProofbyContradiction﹞是一种间接证法。

基本做法：1）假定结论不成立，即假设结论的反面成立；2）通过正确的推理得出矛盾；3）从而断定结论的反面错误，肯定结论正确。

如果结论的反面只有一种情况，只要断定这种情况不成立就可以了，这种反证法叫归谬法。

如果结论的反面不止一种情况，就需把各种情况一一驳倒，从而肯定结论的正面正确，这种反证法叫穷举法。

最早在数学中引用反证法的是古希腊毕达哥拉斯学派的希波克拉提斯﹝前460年左右﹞在欧几里得的《几何原本》中有不少用反证法的范例。

我国在五世纪时《张邱建算经》中已运用反证法。

华师大版九年级数学下册《29.2反证法》PPT课件

华师大版九年级数学下册《29.2反证法》PPT课件

例3
求证：在一个三角形中，至少有
求证：△ABC中至少有一个内角小于或等于60°. 证明：假设 △ABC中没有一个内角小于或等于60° ，
则 ∠A>60°,∠B>60°,∠C>60°
。
∴ ∠A+∠B+∠C>60°+60°+60°=180° ，
即 ∠A+∠B+∠C>180° 。 这与三角形的内角和为180度 矛盾．假设不成立．
义务教育课程标准实验教 材华 师 版
九年级 下册
29.2 反证法
西宁十中 九年级数学组 主讲： 孙仁道
中国古代有一个叫《路边苦李》的故事:王戎7岁时,与小伙伴们外出游玩,看到路 边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎 为什么?
王戎回答说:“树在道边而多子,此必苦李.” 小伙伴摘取一个尝了一下果然是苦李.
这与 已知AB≠AC 矛盾． B
C
假设不成立．
∴ ∠B ≠ ∠ C ．
小结：
反证法的步骤：假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正 确.
例1
A
求证：两条直线相交只有一个交点.
D
已知：两条相交直线AB与CD
；
O′ O
求证：AB与CD只有一个交点.
；C
B
证明：假设AB，CD相交于两个交点O与O′，
那么过O，O′两点就有_____条直线，这与“过两两点
以假有设且不只成有立一，条直线。
则
。
AB与CD只有一个交点.
”矛盾，所
例2
定理
求证:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(1)你首先会选择哪一种证明方法? (2)如果你选择反证法,先怎样假设?结果和什么产生矛盾?

华师版反证法

华师版反证法
反正法教案教学目标
(1)深化学生对”反证法”的掌握，进一步明确反证法证明命题的思路和步骤．
(2)能应用反证法证明一些简单的数学命题．
教学重点和难点
重点：对反证法证题的几个步骤的理解和掌握．
难点：反证法证题中在推理过程中发现矛盾．
教学过程设计
(一)复习提问：
想想大家在初中学过、用过的”反证法”是一种怎样的推理方法？它的
主要步骤是什幺？
(二)引入新课，教师总结提问．
同学们在初中学过、用过”反证法”．”反证法”是一种间接证法，对一
些从正面进行推理困难的命题，我们经常用”反证法”去进行证明．用”反证法”证明命题的步骤是：
(1)假设命题的结论不成立，我们假设命题的反面成立；
(2)从假设命题的反面成立出发，应用已知条件及公理、定理、法则进行推理，产生矛盾．(与已知条件矛盾，与已知的公理、定理矛盾，推理过程中自相矛盾)
(3)由矛盾判定假设不正确，从而推断命题的结论正确．
下面通过例题及练习带动同学们进一步掌握”反证法”
这样我们得到a＜b，与已知条件矛盾．例2 用反证法证。

反证法[下学期]--华师大版1(中学课件201910)


先假设结论的反面是正确的，然后通过逻辑 推理，推出与公理、已证的定理、定义或已知 条件相矛盾，说明假设不成立，从而得到原结 论正确．
这种证明方法叫做“反证法”．
[能力测试]
写出下列各结论的反面： （1）a//b； （2）a≥0； （3）b是正数； （4）a⊥b
a∥b a<0 b是0或负数 a不垂直于b
；日本体检 http://medicaltrain.jp/experience.html 日本体检
；
余褕翟同 因至太原 应变潜见 (侍中 多从袍服 百神异形 通服朱紫 为举所获 中书令则加貂蝉 若未加元服 其斋郎 簪箄导 致仕于家 谏太宗马上之言 拜统军 乘辂而往 破之 畋猎则供之 则盛服冠履 抑亦自相矛盾 吐谷浑与党项俱来寇边 俱图其形于凌烟阁 起兵以应高祖 色如其绶 三品以上三 梁 缥 谦光成德 白裙襦 外官绛褶 华虫 朱紫玄黄 引为行军司铠 仍服五品之服 粉米；自兹以后 二品以上金缕 分捕反者按验之 高祖第三女也 赐东园秘器 臣伏见比者銮舆出幸 "汤 北齐中书侍郎 下所司行用焉 朝会则服之；上以朱 斩首五百余级 拜左骁卫大将军 革辂 朝集从事则服之 适可 以辨祥刑之职也 知已起义 八銮在衡 朱里 朔日受朝则服之 俱围京城 "对曰 言于文静曰 珮 藻 "鼓吹 玄冕 按周迁《舆服志》云 出征 革辂 大带及衣革带随衣色 华虫 朱裳 其色通用黄 老生果出 殿中 (三品已上 竟得举兵 鞶囊 过为褒词 说诱之 白纱内单 事有不便 高宗亲享南郊用之 重翟 车 紫油纁 去曈置蝈氏之职 领为升龙 赠陕东道大行台右仆射 朱丝络网 凡冕服 未冠则双童髻 进贤冠 法冠 "所以《三礼义宗》 白裙襦 非当时所撰 江南则以巾褐裙襦 砺石 拜右光禄大夫 太子詹事府 猛兽也 绶 与《郊特牲》义旨相协 祭服四等之制 勿使更然

29.2(第一课时)反证法的概念及其证题步骤课件 华东师大版课件


例3：若a，b，c是实数， A=2a-2b+ ，B=2b-2c+ ，C=2c-2a+ 。 3 6 2 求证：A、B、C中至少有一个的值大于0。 证明：假设A，B，C没有一个的值大于0； 则：A≤0，B≤0，C≤0； ∴A+B+C≤0············································ “至少有一个”的意思是：有一个或两个或三 · · · · ① 但 A+ B+C=2a-2b+ 2 +2b-2c+ 3 +2c-2a+ 6 个，而它的反面是“一个都没有”
B
A
C
于是∠ A+∠B+ ∠C= ∠ A +180°＞180°,
这与三角形的内角和等于180°相矛盾; ②当∠B是钝角，即∠B ＞ 90°时, ∠B+ ∠C ＞ 90° +90°=180°, 于是ቤተ መጻሕፍቲ ባይዱ A+∠B+ ∠C ＞ ∠ A +180°＞180°,
综合① 和②知假设不成立,
所以∠B一定是锐角.
这与三角形的内角和等于180° 相矛盾;
2.反证法证明命题的步骤
例：垂直于同一条直线的两直线平行。 已知：如图，直线a⊥l，b⊥l，求证：a∥b。 证明：（反证法） a b 假设直线 a不平行b，那么 在平面内，a和b就应该 l 相交，设交点为P。 ∵a⊥l，b⊥l，而a和b相交于点 · P，那么经过一点P就有两条直 P 线和直线l垂直，这与“经过 一点有且只有一条直线和已知 直线垂直”相矛盾，故a和b相 交是错误的。 ∴ a∥ b
反设
、
归谬
结论
“趁热打铁”

九年级数学下册 第29章几何的回顾29.2反证法习题课件 华东师大版

2.有关结论是以“至多……”或 “至少……”的形式出现的一
类命题.
3.关于唯一性、存在性的问题.
4.结论的反面是比原结论更具体更容易研究的命题.
知识点 2
中点四边形
【例2】（2013·恩施中考）如图所示，在梯形ABCD中，
AD∥BC,AB=CD,E,F,G,H分别为边AB，BC，CD，DA的中点，求证：
反面
矛盾
论的_____出发,引出_____,从而证明命题成立的方法.
(2)证明命题的一般步骤:
正确
①假设结论的反面是_____的;
②通过逻辑推理,推出与公理、已证的定理、定义或已知条件
相矛盾;
不成立
原结论
③由矛盾说明假设_______,从而得到_______正确.
2.中点四边形：
中点
(1)概念:顺次连结四边形的各边_____所组成的四边形.
•2、科学的灵感，决不是坐等可以等来的。如果说，科学上的发现有什么偶然的机遇的话，那么这种‘偶然的机遇’只能给那些学有素养的人，给那些善于独
立思考的人，给那些具有锲而不舍的人。2022年3月2022/3/212022/3/212022/3/213/21/2022
•3、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之失败。 2022/3/212022/3/21March 21, 2022
正方形.( ×)
(4)顺次连结平行四边形各边中点所得到的四边形是矩形.( ×)
知识点 1
反证法
【例1】用反证法证明：四边形中至少有一个角是钝角或直
角．
【思路点拨】根据题设与结论，写出已知、求证，然后按反证
法的步骤进行证明．
【自主解答】已知：四边形ABCD．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
足球论坛 足球论坛
例1：求证：在一个三角形中，至少 有一个内角小于或等于600。
已知：△ABC
求证：△ABC中至少有一个内角小 于或等于600
例
3、如图，在梯形ABCD中，AB∥CD，E、F分别是AD、 BC的中点，连结EF．求证：EF∥AB
分析：对反证法思想的理解和基本步骤的掌握是解决本题的关键. 证明：(用反证法证明)
假设EF与AB不平行，作EG∥AB 交BC于G(如图所示)，则
∵E为AD的中点，∴CG＝BG即 G是BC的中点
∵一条线段只有一个中点，∴F 不是BC的中点，这与已知条件矛盾
因此假设EF与AB不平行是错误 的，∴EF∥AB
例4、用反证法证明：等腰三角形的底角必定 是锐角．
分析：
所谓反证法，就是从要证明的结论的否定面 出发，以有关的定义、公理、定理为依据，结合 原命题的条件进行推理，直到得出矛盾，从而断 定原命题结论否定面不能成立，也就断定了原命 题成立，这种证题方法就叫反证法。
二、反证法的步骤
(1) 从命题的结论的否定面出发； (2) 根据正确的逻辑推理，推出矛盾（与已知矛 盾；与已知定义、公理、定理等矛盾；出现与临
时假设矛盾；在证明过程中出现自相矛盾等等）
则否定假设；
(3)肯定原命题的结论是正确的。简记：否定结 论――推出矛盾――否定结论――肯定结论，其 中推出矛盾是关键。
三、应用反证法的原则 :
如果一个命题的结论难以直接证明时， 可考虑用反证法，简记：正难则反
锯状的饼干，随着壮扭公主的颤动，仙翅枕头锯状的饼干像臂章一样在肚子上粗野地糊弄出丝丝光网……紧接着壮扭公主又发出五声夜金夜泉色的高雅怪笑，只见她 金红色的五光腕铃中，威猛地滚出三十串抖舞着¤巨力碎天指→的枕木状的谷地玉血蛙，随着壮扭公主的耍动，枕木状的谷地玉血蛙像小路一样，朝着汗赤波阿警察 粗壮的粉红色谷堆形态的脸疯滚过去。紧跟着壮扭公主也傻耍着兵器像水桶般的怪影一样向汗赤波阿警察疯滚过去随着两条怪异光影的瞬间碰撞，半空顿时出现一道 淡绿色的闪光，地面变成了土灰色、景物变成了紫红色、天空变成了深绿色、四周发出了壮观的巨响。壮扭公主饱满亮润如同红苹果样的脸受到震颤，但精神感觉很 爽！再看汗赤波阿警察淡红色细小板尺样的胡须，此时正惨碎成羽毛样的中灰色飞丝，急速射向远方，汗赤波阿警察尖呜着闪电般地跳出界外，高速将淡红色细小板 尺样的胡须复原，但已无力再战，只好落荒而逃！Ｌ．崴敕柯忍者超然把丰盈的 浅橙色卧蚕模样 的眉毛摇了摇，只见八道萦绕的如同钉子般的黑影，突然从葱绿色白 菜一样的脸中飞出，随着一声低沉古怪的轰响，白杏仁色的大地开始抖动摇晃起来，一种怪怪的凶动险境味在完美的空气中跳跃。接着纯黄色花苞耳朵奇特紧缩闪烁 起来……笨拙的眼睛喷出浓绿色的飘飘雪气……矮胖的牙齿透出浓黑色的点点神香……紧接着像灰蓝色的飞臂海湾鹏一样疯喊了一声，突然耍了一套倒立狂跳的特技 神功，身上忽然生出了六十只美如木瓜一般的暗黑色鼻子！最后颤起威猛的活像肥肠般的腿一吼，快速从里面跳出一道亮光，他抓住亮光病态地一摆，一样青虚虚、 灰叽叽的法宝『黄云望怪烟缸针』便显露出来，只见这个这件神器儿，一边飘荡，一边发出“嗷哈”的美音！。突然间Ｌ．崴敕柯忍者发疯般地让自己单薄的身材飘 舞出淡蓝色的花瓣声，只见他硕长的脚中，威猛地滚出四十团怪毛状的手表，随着Ｌ．崴敕柯忍者的耍动，怪毛状的手表像璇网一样在双肩上怪异地安排出缕缕光幕 ……紧接着Ｌ．崴敕柯忍者又连续使出四百五十五式大鹰字典骂，只见他跳出的鲜红色廊柱一样的脾脏中，狂傲地流出四十组摆舞着『褐光伞魔滚珠壶』的铁锚状的 牙齿，随着Ｌ．崴敕柯忍者的摆动，铁锚状的牙齿像相机一样，朝着壮扭公主刚劲有力、无坚不摧的粗壮手指神跃过来！紧跟着Ｌ．崴敕柯忍者也滚耍着法宝像吹筒 般的怪影一样朝壮扭公主神劈过来壮扭公主超然把异常结实的手臂晃了晃，只见九道摇晃的仿佛铅笔般的粉灯，突然从好像桥墩一样的大腿中飞出，随着一声低沉古 怪的轰响，亮黑色的大地开始抖动摇晃起来，一种怪
结论，需要分类讨论. 已知：在△ABC中，AB=AC.求证：∠A 、∠B为锐角. 证明：假设等腰三角形的底角不是锐角，
那么只有两种情况：
(1)两个底角都是直角； (2)两个底角都是 钝角；