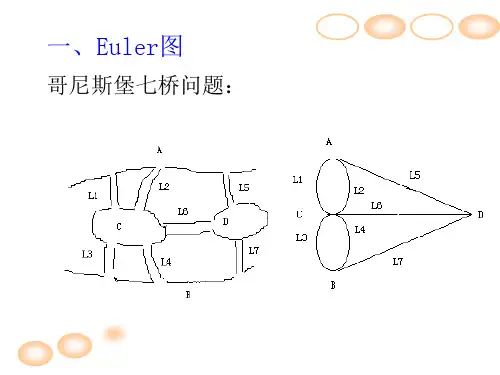
第二节 欧拉图

欧拉图--欧拉通路离散学过欧拉图的⼀些知识今天遇到⼀个题，挺有趣的。

⾸先，欧拉图，是指能从任意⼀点，不重复经过所有边能回到起点的图便是欧拉图。

这个路也叫欧拉回路。

次之，欧拉通路，任意⼀点，不重复经过所有边，不回到起点。

这个路叫欧拉通路。

记得书上的分析是从出⼊度来分析的，对于⽆向图，⼀点的度即是该点连接的边数。

对于有向图，就分为出度和⼊度。

欧拉回路：⽆向图中，所有点都是偶度点，存在欧拉回路。

有向图中，所有点的出度等于⼊度，存在欧拉回路。

欧拉通路：⽆向图中，满⾜有且仅有0或1对奇度点，即存在欧拉通路（奇度点分别为起点和终点）。

有向图中，满⾜有且仅有0或1对点的出⼊度差值为1，即存在欧拉通路（⾃然，出度多的那个是起点，⼊度多的那个是终点）。

那么，对代码来说，这也很容易实现，但是但是但是！我wa了很多次错误点：1.⼤写字母的ascll码⽐⼩写字母ascll码⼤。

2.这题是欧拉通路，没注意奇度点的先后性，也就是，如果有奇度点，得从奇度点开始遍历，⽽不是直接从⼩到⼤找第⼀个有度的字母，也就是得遍历两次找起点。

3.有重复边的存在，不能简单矩阵存图。

4.这题有重复字母，a->a这种也有，遇到⼀组数据如下6aabbccabbccaaabbcca这组数据顺序遍历输出会编程aabbca，少⼀个c，这是bfs遍历的问题，也即存在最后连不起来的情况。

另外，对于dfs也要注意⼀个地⽅，就是需要结束时去存答案，⽽不是开始遍历前存答案。

但是为什么：这样逆序输出从⼩到⼤dfs搜索的答案能保证最后的答案还是字典序最⼩的？这个问题还不是很明⽩，暂留⼀问吧。

5.连通性问题（虽然这题没出到这种数据，但是也确实是⼀个wa点）最后就贴上上述题的代码吧。

#include<iostream>#include<cstring>#include<cstdlib>#include<vector>#include<queue>#include<cmath>#include<map>#include<algorithm>using namespace std;#define N 202#define mt(x) memset(x,0,sizeof x) typedef long long ll;void cn(ll x){cout<<x<<endl;}void cs(string x){cout<<x<<endl;} vector<int>vc[N];int n;int vis[N][N],c;char ans[N];int edge[N];void add(int x,int y){vc[x].push_back(y);vc[y].push_back(x);vis[x][y]++;vis[y][x]++;edge[x]++;edge[y]++;}void find(int x){for(int i='A';i<='z';++i){if(vis[x][i]){vis[x][i]--;vis[i][x]--;find(i);}}ans[c++]=x;}bool pd(){int cnt=0,t=0;for(int i='A';i<='z';++i)if(edge[i]%2){cnt++;if(!t)t=i;}if(!t){for(int i='A';i<='z';++i)if(edge[i]){t=i;break;}}if(cnt&&cnt!=2)return false;find(t);return true;}void PR(){while(c)cout<<ans[--c];cout<<endl;}void solve(){cin>>n;mt(edge);for(int i=0;i<n;++i){string s;cin>>s;add(s[0],s[1]);}if(!pd()||c!=n+1)cs("No Solution"); else PR();}int main(){ios::sync_with_stdio(false);cin.tie(0);solve();return0;}。

七年级上册数学第六单元知识点七年级上册数学第六单元学习的内容是关于欧拉图的知识。

欧拉图起源于18世纪，是图论中的一种基本概念。

在这一单元中，我们将学习欧拉图的基础概念、性质及其应用，并掌握欧拉图的构造方法。

一、欧拉图的基础概念欧拉图是指一种特殊的图，这种图包含了所有节点都能够连通（即是连通图）且每个节点的度数都是偶数的图。

欧拉图有两种形式：欧拉回路和欧拉通路。

欧拉回路：在一张图中，如果从一个节点出发，恰好经过所有的边，且最后回到原始节点，那么这张图就包含欧拉回路。

欧拉通路：在一张图中，如果存在一条路径可以经过所有边，但是不需要回到原始节点，那么这张图就包含欧拉通路。

二、欧拉图的性质欧拉图的性质有如下几点：1、欧拉回路存在的判断条件：该图所有节点的度数都是偶数。

2、欧拉通路存在的判断条件：该图有且仅有两个奇度数节点（度数为奇数的节点）（或者无奇度数节点）。

3、若一张无向图中存在欧拉回路或欧拉通路，则一定是连通图。

三、欧拉图的构造方法1、欧拉回路的构造方法：每次从一个节点出发遍历该节点所连边中没有被遍历过的边。

一直遍历下去，直到回到起点。

2、欧拉通路的构造方法：选择一个奇度数节点作为起点，从该节点开始遍历该节点所连边中没有被遍历过的边。

当无法再走下去的时候，进入另一个未遍历到的奇数度节点继续遍历。

一直遍历下去，直到所有边都被遍历过为止。

四、欧拉图在实际应用中的意义欧拉图的2个重要性质：所有节点的度数都是偶数或者只有2个奇度数节点，意味着欧拉图是很有规律的。

因此，在我们的现实世界中很多事物都可以用欧拉图来表示。

例如，在城市规划中，欧拉回路可以表示为一个完美的环路，有可能在一个城市中形成一个中心广场。

在网络优化方面，欧拉图可以用来控制数据的流动，以实现更好的性能。

在实际应用中，学习欧拉图可以使我们更好地理解和分析问题，从而提高解决问题的能力。

五、总结欧拉图是图论中的基本概念，主要包括欧拉回路和欧拉通路。

欧拉图（离散数学）
定义
欧拉回路：通过图中每条边⼀次且仅⼀次，并且过每⼀顶点的回路。

欧拉图：具有欧拉回路的图。

欧拉通路：通过图中每条边⼀次且仅⼀次，并且过每⼀顶点的通路。

半欧拉图：具有欧拉通路⽽⽆欧拉回路的图。

连通：图中从⼀个顶点到达另⼀顶点，若存在⾄少⼀条路径，则称这两个顶点是连通着的。

连通图：⽆向图中，如果任意两个顶点之间都能够连通，则称此⽆向图为连通图。

判断
⽆向图 G 有欧拉通路：图连通，G 中奇度顶点的数⽬为2（分别为欧拉通路的两个端点）。

⽆向图 G 是欧拉回路：图连通，G 中每个顶点都是偶度顶点。

有向图 G 有欧拉通路：图连通，G 中除两个顶点外（起点与终点），其余顶点的⼊度都等于出度。

其中起点的⼊度⽐出度⼩1，终点的⼊度⽐出度⼤1。

有向图 G 有欧拉回路：图连通，G 中所有顶点的⼊度等于出度。