高二数学推理与证明

推理与证明对于数学的学习，应具备“能力”，其中本章的“推理与证明”就是一种重要的“逻辑思维”能力形式．通过本章的复习，要有着扎实的推理、论证能力，以增强对问题的敏锐的观察，深刻的理解、领悟能力．一．推理部分1．知识结构：2．和情推理：归纳推理与类比推理统称为和情推理．①归纳推理：由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或有个别事实概括出一般结论的推理，称为归纳推理．②类比推理：由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理称为类比推理．③定义特点；归纳推理是由特殊到一般、由部分到整体的推理；而类比推理是由特殊到特殊的推理；都能由已知推测、猜想未知，从而推理结论．但是结论的可靠性有待证明．例如：已知2()53f n n n =-+-，可以(1)10f =>，(2)30,f =>(3)30,(4)10f f =>=>，于是推出：对入任何n N *∈，都有()0f n >；而这个结论是错误的，显然有当5n =时，(5)30f =-<．因此，归纳法得到的结论有待证明．例如：“在平面内与同一条直线垂直的两条直线平行”；类比线与线得到：“在空间与同一条直线垂直的两条直线平行“；显然此结论是错误的”．类比线与面得到：在空间与同一个平面垂直的两个平面平行；显然此结论是错误的．④推理过程：从具体问题出发 观察、分析、比较、联想 归纳、类比 猜想．3．演绎推理：从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为演绎推理（逻辑推理）．①定义特点：演绎推理是由一般到特殊的推理；②数学应用：演绎推理是数学中证明的基本推理形式；推理模式：“三段论”：ⅰ大前提：已知的一般原理（M 是P ）；ⅱ小前提：所研究的特殊情况（S 是M ）；ⅲ结论：由一般原理对特殊情况作出判断（S 是P ）；集合简述：ⅰ大前提：x ∈M 且x 具有性质P ；ⅱ小前提：y ∈S 且S ⊆M ；ⅲ结论： y 也具有性质P ；例题1．若定义在区间D 上的函数()f x 对于D 上的n 个值12,,n x x x ，总满足[]12121()()()()n n x x x f x f x f x f n n ++++++≤，称函数()f x 为D 上的凸函数；现已知()sin f x x =在(0,)π上是凸函数，则ABC ∆中，sin sin sin A B C ++的最大值是 ．解答：由[]12121()()()()n n x x x f x f x f x f n n ++++++≤（大前提）因为()sin f x x =在(0,)π上是凸函数 （小前提）得()()()3()3A B C f A f B f C f ++++≤ （结论）即sin sin sin 3sin 3A B C π++≤=因此，sin sin sin A B C ++的最大值是2 注：此题是一典型的演绎推理“三段论”题型4.和情推理与演绎推理的关系：①和情推理是由特殊到一般的推理，演绎推理是由一般到特殊的推理；②它们又是相辅相成的，前者是后者的前提，后者论证前者的可靠性；例2．设()2x x a a f x -+=，()2x xa a g x --=（其中0a >且1a ≠） （1）5＝2＋3请你推测(5)g 能否用(2),(3),(2),(3)f f g g 来表示；（2）如果（1）中获得了一个结论，请你推测能否将其推广.解答:（1）由(3)(2)(3)(2)f g g f +＝332a a -+222a a --＋332a a --222a a -+ ＝552a a -- 又(5)g ＝552a a -- 因此，(5)g ＝(3)(2)(3)(2)f g g f +（2）由(5)g ＝(3)(2)(3)(2)f g g f +即(23)g +＝(3)(2)(3)(2)f g g f +于是推测()g x y +＝()()()()f x g y g x f y + 证明：因为：()2x x a a f x -+=，()2x xa a g x --=（大前提） 所以()g x y +＝2x y x ya a ++-， ()g y ＝2y y a a --，()f y ＝2y ya a -+，（小前提及结论） 所以()()()()f x g y g x f y +＝2x x a a -+2y y a a --＋2x x a a --2y ya a -+ ＝2x y x ya a ++-＝()g x y + 解题评注：此题是一典型的由特殊到一般的推理，构造(23)g +＝(3)(2)(3)(2)f g g f +是此题的一大难点，要经过观察、分析、比较、联想而得到；从而归纳推出一般结论()g x y +＝()()()()f x g y g x f y +．二．证明部分1．知识结构2．综合法与分析法①综合法；利用已知条件和某些数学定义、公理、定理等出发，经过一系列推理论证，推导出所要证明的结论成立．②分析法：从要证明的结论出发逐步寻求使它成立的充分条件，直至把要证明的结论归结为判别一个明显成立的条件为止．③综合应用：在解决问题时，经常把综合法与分析法和起来使用；使用分析法寻找成立的条件，再用综合法写出证明过程．例3．已知：0a b >>，求证：22()()828a b a b a b ab a b-+-<-< 证明：因为0a b >> 所以22()()828a b a b a b ab a b-+-<< ⇔222()()()44a b a b a b a b--<< ⇔|22a b a b<< ⇔2a b a b a b<< ⇔121b a a b < ⇔1b a a b<又由已知0a b >>1b a a b<<成立． 由于以上分析步步等价，因此步步可逆．故结论成立．解题评注：(1)以上解答采用恒等变形，其实质从上往下属于分析法，反之属于综合法．(2)1b a a b<,(0a b >>)是结论成立的充要条件,当然找到了结论成立的充分条件就可以了.例4.求证抛物线22(0)y px p =>，以过焦点的弦为直径的圆必与2p x =-相切. 证明：（如图）作AA ／、BB ／垂直准线，取AB 的中点M ，作MM ／垂直准线. 要证明以AB 为直径的圆与准线相切只需证｜MM ／｜＝12｜AB ｜ 由抛物线的定义：｜AA ／｜＝｜AF ｜，｜BB ／｜＝｜BF ｜所以｜AB ｜＝｜AA ／｜＋｜BB ／｜因此只需证｜MM ／｜＝12（｜AA ／｜＋｜BB ／｜） 根据梯形的中位线定理可知上式是成立的. 所以以过焦点的弦为直径的圆必与2p x =-相切. 以上解法同学们不难以综合法作出解答.解题评注:分析法是从结论出发寻找证题思路的一种重要的思维方法,特别是题设和结论相结合,即综合法与分析法相结合,可使很多较为复杂的问题得到解决.3.数学归纳法一般地，证明一个与正整数ｎ有关的命题的步骤如下：（1）（归纳奠基）证明当ｎ取第一个值ｎ0时命题成立；（2）（归纳递推）假设ｎ＝k （0(,)k n k n ≥∈*时命题成立，证明当1n k =+ 时命题也成立。

高二数学推理与证明试题答案及解析1.下列推理合理的是（）A．是增函数，则B．因为，则C．为锐角三角形，则D．直线，则【答案】C【解析】根据题意，由于是增函数，则或者f’(x)=0在个别点成立，故错误对于B，因为，则显然不成立，对于D直线，则，可能斜率都不存在，故错误，故选C.【考点】推理与证明点评：主要是考查了合情推理的运用，属于基础题。

2.对命题“正三角形的内切圆切于三边的中点”可类比猜想出：正四面体的内切球切于四面都为正三角形的什么位置？（）A．正三角形的顶点B．正三角形的中心C．正三角形各边的中点D．无法确定【答案】B【解析】根据题意，由于命题“正三角形的内切圆切于三边的中点”可类比猜想出：正四面体的内切球切于四面都为正三角形的中心，故可知答案为B.【考点】类比推理点评：主要是考查了类比推理的运用，属于基础题。

3.对大于或等于2的自然数的次方幂有如下分解方式：根据上述分解规律，若的分解中最小的数是73，则的值为 .【答案】9【解析】根据题意，可知，，，，那么可知的分解中最小的数是73，那么可知m的值为9.故答案为9.【考点】归纳推理点评：主要是考查了归纳推理的运用，属于基础题。

4.观察式子：1＋<，1＋＋<，1＋＋＋<，，则可归纳出一般式子为() A．1＋＋＋＋<(n≥2)B．1＋＋＋＋<(n≥2)C．1＋＋＋＋<(n≥2)D．1＋＋＋＋<(n≥2)【答案】C【解析】根据题意，由于观察式子：1＋<，1＋＋<，1＋＋＋<，左边是n 个自然数平方的倒数和，右边是项数分之项数的二倍减去1，那么可得到，推广到一般1＋＋＋＋<(n≥2)，故选C.【考点】归纳推理点评：主要是考查了归纳推理的基本运用，属于基础题。

5.在平面上，若两个正三角形的边长比为，则它们的面积比为，类似地，在空间中若两个正四面体的棱长比为，则它们的体积比为____________。

第二章推理与证明知识点：1、归纳推理把从个别事实中推演出一般性结论的推理,称为归纳推理(简称归纳).简言之,归纳推理是由部分到整体、由特殊到一般的推理。

归纳推理的一般步骤：•通过观察个别情况发现某些相同的性质；•从已知的相同性质中推出一个明确表述的一般命题（猜想）；•证明（视题目要求，可有可无）.2、类比推理由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理称为类比推理（简称类比）．简言之，类比推理是由特殊到特殊的推理.类比推理的一般步骤：•找出两类对象之间可以确切表述的相似特征；•用一类对象的已知特征去推测另一类对象的特征，从而得出一个猜想；•检验猜想。

3、合情推理归纳推理和类比推理都是根据已有的事实，经过观察、分析、比较、联想，再进行归纳、类比，然后提出猜想的推理.归纳推理和类比推理统称为合情推理，通俗地说，合情推理是指“合乎情理”的推理.4、演绎推理从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为演绎推理．简言之，演绎推理是由一般到特殊的推理.演绎推理的一般模式———“三段论”，包括⑴大前提-----已知的一般原理；⑵小前提-----所研究的特殊情况；⑶结论-----据一般原理，对特殊情况做出的判断．5、直接证明与间接证明⑴综合法：利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明的结论成立.要点：顺推证法；由因导果.⑵分析法：从要证明的结论出发，逐步寻找使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止.要点：逆推证法；执果索因.⑶反证法：一般地，假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明了原命题成立.的证明方法.它是一种间接的证明方法.反证法法证明一个命题的一般步骤：(1)（反设）假设命题的结论不成立；(2)（推理）根据假设进行推理,直到导出矛盾为止；(3)（归谬）断言假设不成立；(4)（结论）肯定原命题的结论成立.6、数学归纳法数学归纳法是证明关于正整数n的命题的一种方法.用数学归纳法证明命题的步骤;（1）（归纳奠基）证明当n 取第一个值*00()n n N ∈时命题成立；（2）（归纳递推）假设*0(,)n k k n k N =≥∈时命题成立，推证当1n k =+时命题也成立.只要完成了这两个步骤，就可以断定命题对从0n 开始的所有正整数n 都成立. 考点：无第三章 数系的扩充与复数的引入知识点：一:复数的概念(1) 复数:形如(,)a bi a R b R +∈∈的数叫做复数，a 和b 分别叫它的实部和虚部.(2) 分类:复数(,)a bi a R b R +∈∈中,当0b =,就是实数; 0b ≠,叫做虚数;当0,0a b =≠时,叫做纯虚数.(3) 复数相等:如果两个复数实部相等且虚部相等就说这两个复数相等.(4) 共轭复数:当两个复数实部相等,虚部互为相反数时,这两个复数互为共轭复数.(5) 复平面:建立直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴，y 轴除去原点的部分叫做虚轴。

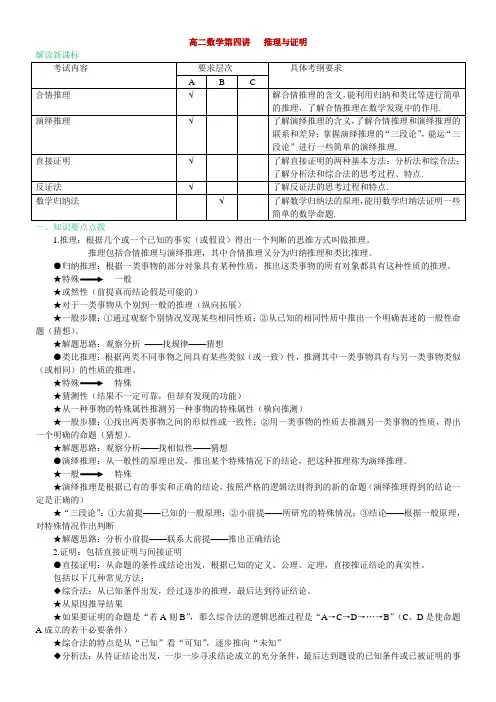
高二数学第四讲推理与证明解读新课标一、知识要点点拨1.推理：根据几个或一个已知的事实（或假设）得出一个判断的思维方式叫做推理。

推理包括合情推理与演绎推理，其中合情推理又分为归纳推理和类比推理。

●归纳推理：根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理。

★特殊一般★或然性（前提真而结论假是可能的）★对于一类事物从个别到一般的推理（纵向拓展）★一般步骤：①通过观察个别情况发现某些相同性质；②从已知的相同性质中推出一个明确表述的一般性命题（猜想）。

★解题思路：观察分析——找规律——猜想●类比推理：根据两类不同事物之间具有某些类似（或一致）性，推测其中一类事物具有与另一类事物类似（或相同）的性质的推理。

★特殊特殊★猜测性（结果不一定可靠，但却有发现的功能）★从一种事物的特殊属性推测另一种事物的特殊属性（横向推测）★一般步骤：①找出两类事物之间的形似性或一致性；②用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）。

★解题思路：观察分析——找相似性——猜想●演绎推理：从一般性的原理出发，推出某个特殊情况下的结论，把这种推理称为演绎推理。

★一般特殊★演绎推理是根据已有的事实和正确的结论，按照严格的逻辑法则得到的新的命题（演绎推理得到的结论一定是正确的）★“三段论”：①大前提——已知的一般原理；②小前提——所研究的特殊情况；③结论——根据一般原理，对特殊情况作出判断★解题思路：分析小前提——联系大前提——推出正确结论2.证明：包括直接证明与间接证明●直接证明：从命题的条件或结论出发，根据已知的定义、公理、定理，直接推证结论的真实性。

包括以下几种常见方法：◆综合法：从已知条件出发，经过逐步的推理，最后达到待证结论。

★从原因推导结果★如果要证明的命题是“若A则B”，那么综合法的逻辑思维过程是“A→C→D→…→B”（C、D是使命题A成立的若干必要条件）实。

★从结果追溯原因★如果要证明的命题是“若A 则B ”，那么分析法的逻辑思维过程是“B ←D ←C ←…←A ”（C 、D 是使B 成立的若干充分条件）★分析法的特点是执果索因，从“未知”看“需知”，逐步靠拢“已知”综合法与分析法的联系：运用综合法叙述推理过程，简明扼要，条理清楚，但是，前进的道路往往不止一条，所以每逢歧路，选择甚难，有时从条件出发，想不到从何处入手才有效，而分析法执果索因，寻根容易，便于思考。

高二推理与证明知识点推理和证明是高中数学中的重要内容之一，它们不仅是数学思维的核心，也是培养学生逻辑思维和分析能力的有效方式。

在高二阶段，学生需要掌握一定的推理和证明的知识点，下面将介绍其中的几个重要内容。

一、命题与命题联结词在推理与证明中，命题是基础概念。

命题是陈述性的句子，要么是真的，要么是假的。

命题可以使用命题联结词进行逻辑联结，常见的命题联结词有“与”、“或”、“非”等。

例如，p与q的合取命题可以表示为p∧q，表示p并且q同时为真；p或q的析取命题可以表示为p∨q，表示p或q至少有一个为真；非p的命题可以表示为¬p，表示p的否定。

二、条件与充分必要条件条件是推理与证明中常用的一种命题形式，它具有“如果...，那么...”的形式。

其中，前件称为充分条件，后件称为必要条件。

例如，若p，则q，表示p是q的充分必要条件。

在证明中，我们通常需要探究条件的真假关系并进行推理推导。

三、直接证明直接证明是常用的证明方法之一。

它通过运用已知条件和数学推理，按照一定的逻辑思路来证明命题的真实性。

直接证明的基本框架是：先假设命题为真，然后基于这一假设，利用数学定理、定义、公理等进行推导，最终得出结论，证明命题是真的。

在直接证明过程中，需要严密的逻辑推理和合理的论证步骤。

四、间接证明间接证明也是常用的证明方法之一，它通过假设命题的否定形式为真，然后通过推理推导推出一个矛盾的结论，从而得出原命题为真的结论。

间接证明通常运用反证法，即假设命题不成立，然后通过推理推导出一个与已知条件矛盾的结论，从而否定了假设，证明了原命题的真实性。

五、反证法反证法是一种特殊的间接证明方法，它通过假设命题的否定形式为真，然后推导出一个明显的矛盾结论，从而否定了假设，得出原命题为真的结论。

反证法常用于证明某些数论命题，其中典型的例子就是证明“根号2是无理数”。

反证法的关键在于找到一个能够导致矛盾结论的假设，从而否定假设，证明原命题的真实性。

推理与证明(推荐时间：50分钟)一、选择题1．(2010·山东)观察(x 2)′＝2x ，(x 4)′＝4x 3，(cos x )′＝－sin x ，由归纳推理可得：若定义在R 上的函数f (x )满足f (－x )＝f (x )，记g (x )为f (x )的导函数，则g (－x )等于( )A ．f (x )B ．－f (x )C ．g (x )D ．－g (x )2．已知数列{a n }的前n 项和S n ＝n 2a n (n ≥2)，而a 1＝1，通过计算a 2，a 3，a 4，猜想a n 等于( )A.2(n ＋1)2B.2n (n ＋1)C.22n －1D.22n －13．用反证法证明命题：若整数系数一元二次方程ax 2＋bx ＋c ＝0 (a ≠0)有有理根，那么a ，b ，c 中至少有一个是偶数时，下列假设中正确的是( )A ．假设a ，b ，c 都是偶数B ．假设a ，b ，c 都不是偶数C ．假设a ，b ，c 至多有一个是偶数D ．假设a ，b ，c 至多有两个是偶数4．(2011·江西)观察下列各式：72＝49,73＝343,74＝2 401，…，则72 011的末两位数字为( )A ．01B ．43C ．07D ．495．定义一种运算“*”：对于自然数n 满足以下运算性质：（ⅰ）1*1=1,(ⅱ)( n +1)*1= n *1+1,则n *1等于（ ）A ．nB ．n ＋1C ．n －1D ．n 26．已知数列{a n }中，a n ∈(0，12)，a n ＋1＝38＋12·a 2n，则数列{a n }是( ) A ．单调递增数列B ．单调递减数列C ．摆动数列D ．先递增后递减数列二、填空题7．(2011·北京)设A (0,0)，B (4,0)，C (t ＋4,3)，D (t,3) (t ∈R )．记N (t )为平行四边形ABCD 内部(不含边界)的整点的个数，其中整点是指横、纵坐标都是整数的点，则N (0)＝________；N (t )的所有可能取值为________．8．(2011·山东)设函数f (x )＝x x ＋2(x >0)，观察： f 1(x )＝f (x )＝x x ＋2， f 2(x )＝f (f 1(x ))＝x 3x ＋4， f 3(x )＝f (f 2(x ))＝x 7x ＋8， f 4(x )＝f (f 3(x ))＝x 15x ＋16， ……根据以上事实，由归纳推理可得：当n ∈N *且n ≥2时，f n (x )＝f (f n －1(x ))＝________.9．若数列{a n }的通项公式a n ＝1(n ＋1)2，记f (n )＝2(1－a 1)·(1－a 2)…(1－a n )，试通过计算f (1)，f (2)，f (3)的值，推测出f (n )＝________.10．在公比为4的等比数列{b n }中，若T n 是数列{b n }的前n 项积，则有T 20T 10，T 30T 20，T 40T 30仍成等比数列，且公比为4100；类比上述结论，在公差为3的等差数列{a n }中，若S n 是{a n }的前n 项和，则有________________________也成等差数列，该等差数列的公差为________．三、解答题11．在数列{a n }中，a 1＝1，当n ≥2时，其前n 项和S 满足S 2n ＝a n ⎝⎛⎭⎫S n －12. (1)求1S 2，1S 3，1S 4，…，并求1S n(不需证明)； (2)求数列{a n }的通项公式.12.观察下列三角形数表假设第n 行的第二个数为a n (n ≥2，n ∈N *)，(1)依次写出第六行的所有6个数字；(2)归纳出a n ＋1与a n 的关系式并求出a n 的通项公式．13．已知数列{a n }中，a 4＝28，且满足a n ＋1＋a n －1a n ＋1－a n ＋1＝n . (1)求a 1，a 2，a 3；(2)猜想{a n }的通项公式并证明．答案1．D 2．B 3．B 4．B 5．A 6．A7．6 6,7,8 8.x (2n －1)x ＋2n 9.n ＋2n ＋1 10．S 20－S 10，S 30－S 20，S 40－S 30300 11．解 (1)当n ≥2时，由a n ＝S n －S n －1和S 2n ＝a n ⎝⎛⎭⎫S n －12，得S 22＝(S 2－S 1)⎝⎛⎭⎫S 2－12，得1S 2＝1＋2S 1S 1＝2＋11＝3，由S 23＝(S 3－S 2)⎝⎛⎭⎫S 3－12，得1S 3＝2＋1S 2＝5，由S 24＝(S 4－S 3)⎝⎛⎭⎫S 4－12，得1S 4＝2＋1S 3＝7，…由S 2n ＝(S n －S n －1)⎝⎛⎭⎫S n －12，得1S n ＝2＋1S n －1＝2n －1.(2)由(1)知，S n ＝12n －1，当n ≥2时，a n ＝S n －S n －1＝12n －1－12n －3＝－2(2n －1)(2n －3)，显然，a 1＝1不符合上述表达式，所以数列{a n }的通项公式为a n ＝⎩⎨⎧ 1，n ＝1，－2(2n －1)(2n －3)，n ≥2.12．解 (1)第六行的所有6个数字分别是6,16,25,25,16,6.(2)依题意a n ＋1＝a n ＋n (n ≥2)，a 2＝2，a n ＝a 2＋(a 3－a 2)＋(a 4－a 3)＋…＋(a n －a n －1)＝2＋2＋3＋…＋(n －1)＝2＋(n －2)(n ＋1)2， 所以a n ＝12n 2－12n ＋1(n ≥2)． 13．解 (1)a n ＋1＋a n －1a n ＋1－a n ＋1＝n . 当n ＝3时，a 4＋a 3－1a 4－a 3＋1＝3. ∵a 4＝28，∴a 3＝15；当n ＝2时，a 3＋a 2－1a 3－a 2＋1＝2. ∵a 3＝15，∴a 2＝6；当n ＝1时，a 2＋a 1－1a 2－a 1＋1＝1. ∵a 2＝6，∴a 1＝1.(2)猜想a n ＝n (2n －1)．①当n ＝1时，a 1＝1，而a 1＝1×(2×1－1)＝1，等式成立． ②假设当n ＝k 时，等式成立， 即a k ＝k (2k －1)．则当n ＝k ＋1时，a k ＋1＋a k －1a k ＋1－a k ＋1＝k ，a k ＋1＋k (2k －1)－1a k ＋1－k (2k －1)＋1＝k ， 整理，得(1－k )a k ＋1＝－2k 3－k 2＋2k ＋1 ＝(2k ＋1)(1－k 2)，a k ＋1＝(1＋k )(2k ＋1)＝(k ＋1)[2(k ＋1)－1]， 等式也成立．综合①②可知，n ∈N *时，等式成立．。

人教版高二数学教材的数学推理与证明数学是一门理性思维的学科，而数学推理与证明则是培养学生逻辑思维能力和创造力的关键。

作为人教版高二数学教材的重要内容，数学推理与证明不仅为学生提供了解题的思路和方法，还通过各种题型和例题，引导学生从观察、猜想、证明三个阶段，逐步提高他们的证明能力。

本文将从几个方面介绍人教版高二数学教材中关于数学推理与证明的内容，并总结其教学特点和意义。

一、数学推理与证明在数学教材中的位置人教版高二数学教材将数学推理与证明作为数学教学的重点和难点内容之一，并在各章节中设置了专门的篇章来介绍和讲解。

数学推理与证明从几何学、代数学等不同角度进行，覆盖了高二数学教学的几个重要领域。

通过数学推理与证明的学习，学生能够更好地理解和运用所学的数学知识，提高数学思维能力和解题能力。

二、数学推理与证明的教学内容1. 几何推理与证明：人教版高二数学教材中的几何部分，重点介绍了几何知识的推理与证明。

学生通过学习几何定理和性质，从观察实例出发，逐步形成猜测和推理的能力。

同时，教材提供了大量的例题和习题，引导学生进行几何证明，培养他们的证明能力。

2. 代数推理与证明：除了几何推理与证明，人教版高二数学教材还涉及了代数推理与证明。

通过学习代数方程、不等式、函数等内容，培养学生的代数推理与证明能力。

同时，教材还提供了丰富的例题和实践题，帮助学生运用代数推理与证明解决实际问题。

3. 综合推理与证明：在数学学习中，很多问题需要进行多学科的综合推理与证明。

人教版高二数学教材中，通过真实场景、实际问题等方式，引导学生进行数学知识的综合运用和推理证明，培养他们的综合思维和解决问题的能力。

三、数学推理与证明的教学特点1. 逐步推进：人教版高二数学教材的数学推理与证明教学，从简单到复杂，从易到难，逐步推进。

通过例题和习题的设置，让学生在观察、猜想、证明的过程中，逐渐提高他们的证明能力。

2. 强调思维方法：在数学推理与证明的教学过程中，人教版高二数学教材注重培养学生的思维方法。

《推理与证明》要点解读一、合情推理与演绎推理要点解读1.合情推理合情推理是根据实验和实践的结果、个人的经验和直觉，已有的事实和正确的结论(定义、定理、公理、定理等)，推测出某些结果的推理方式.其中，归纳推理和类比推理是最常见的合情推理.(1)归纳推理:根据一类事物中部分事物具有某种属性,推断该类事物中每一个事物都有这种属性,我们将这种推理方式称为归纳推理.剖析:①利用归纳推理得到的结论不一定正确.如果归纳的个别情况越多,越具有代表性,那么推广的一般性命题也就越可靠.②归纳推理的一般模式:S1具有P,S2具有P,…,S n具有P(S1,S2,…,S n是A类事件的对象),则A类事件具有P.③归纳推理的一般步骤:首先,观察特例发现某些相似性(特例的共性或一般规律);然后,把这种相似性推广为一个明确表述的一般性命题（猜想）.(2)类比推理:根据一类对象的其他特征,推断另一类对象也具有类似的其他特征,我们把这种推理过程称为类比推理.剖析: ①与归纳推理类似, 类比推理所得结论也不一定为真.如果类比的相似性越多,相似性之间越相关,那么类比得到的结论也就越可靠．②类比推理的思维过程:观察、比较→联想、类推→猜测新的结论.③类比推理的一般步骤：首先,找出两类事物之间的相似性或一致性;然后,用一类事物的性质去推测另一类事物的性质,得出一个明确的命题（猜想）．④归纳推理与类比推理的对比:归纳推理是从特殊到一般的思想方法,类比推理是由此及彼和由彼及此的联想方法;归纳和类比都离不开观察、分析、对比、联想,许多数学知识都是通过归纳与类比发掘出来的;归纳和类比均不能做为严格的证明工具.2.演绎推理演绎推理是根据已知的事实和正确的结论,按照严格的逻辑法则得到新结论的推理过程.剖析:①从思维过程的指向看，演绎推理是以某一类事物的一般判断为前提,而作出关于该类事物中某一具体对象的判断的思维形式,因此它是从一般到特殊的推理.②演绎推理是数学证明的基本推理形式,也是公理化体系所采用的推理形式,因此它可以做为严格的证明工具.3.合情推理与演绎推理的比较(1)从推理形式上看:归纳推理是由部分到整体、个别到一般的推理; 类比推理是两类事物特征之间的推理,是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理.(2)从所得结论上看:合情推理的结论不一定正确,有待进一步证明;而演绎推理在大前提、小前提和推理形式都正确的前提下,得到的结论一定正确.(3)从数学角度看:合情推理发现证明思路;演绎推理证明结论.(4)联系:合情推理与演绎推理是相辅相成的,前者是后者的前提,后者论证前者的可靠性．二、合情推理与演绎推理典例剖析例 1 已知113,1(1,2,)n n n a a a a n +=-==,n A 表示数列{}n a 的前n 项之积,则2011A = .分析:要求{}n a 的前n 项之积，应首先明确数列{}n a 的通项,而由题设直接求通项比较困难,故可考虑计算出{}n a 的前几项，从中寻找规律，从而进一步猜想、归纳出通项n a解:由13,a =112a a a -=1,得223a =;由2231,a a a -=得31;2a =- 由3341a a a -=,得43a =.通过观察、分析、归纳猜想知{}n a 是周期为3的数列,所以由归纳推理得 67020091231()3A a a a a =⋅=.点评:归纳推理的关键是发现规律,此时切忌凭空想象，而应一步一步地进行分析，通过观察、分析前几个已知或易得出的特殊现象(如数列的前几项)，找出规律性,即可归纳出相相应的结论.例 2 到圆心距离相等的两条弦的弦长相等，类比上述性质,在球中相应的特性为 .分析:本题是平面图形与空间图形的类比,只要搞懂圆的圆心与弦应与球的哪两个量类比，答案便跃然纸上.解:分析圆(球)的定义是在平面内(在空间中)到一定点的距离等于定长的点的集合,圆(球)是中心对称图形,对称中心是圆(球)心,故由圆心联想到球心.圆心和弦的中点的连线垂直于弦,球心和截面圆心的连线垂直于截面,故由圆的弦联想到球的截面圆.通过联想、类比可得:到球心距离相等的两个截面圆面积相等.点评:类比推理主要涉及两个模型:一个是已知的、熟悉的模型,另一个是需要我们建立的新模型,为导出新模型,必须抓住已知模型的本质特征，分析与新模型在性质上的相似性，同时关注其差异性，进而作出正确的类比迁移.三、直接证明与间接证明要点解读在前面我们已经知道合情推理和演绎推理都是根据某些已知判断来确定一个新的判断的思维过程.其中演绎推理在大前提小前提都正确的情况下所得的结论一定正确，而合情推理（归纳、类比等）所猜测得到的结论不一定正确，必须通过逻辑（演绎）推理的方式加以证明.下面继续研究两类基本的证明方法———直接证明与间接证明.1.综合法和分析法是直接证明中最基本的两种证法，也是证明数学问题时最常用的思维方式.（1）综合法：利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明的结论成立的证明方法.又叫顺推证法或由因导果法.其推理方式可用框图表示为：其中P表示已知条件、已有的定义、公理、定理等，Q表示所要证明的结论，12Q Q，，表示中间结论．综合法常用的表达格式为：P∵，1Q∴；又∵，2Q∴；，nQ∴；又∵，Q∴．（2）分析法：从要证明的结论出发，对其进行分析和转化，逐步寻求使它成立的充分条件，直到最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止的证明方法.又叫逆推证法或执果索因法.其推理方式可用框图表示为：其中Q表示要证明的结论，1230Q Q Q Q，，，，分别表示使12nQ Q Q Q，，，，成立的充分条件，Q表示最后寻求到的一个明显成立的条件．分析法常用的表达格式为：要证Q，只需证1Q，只需证2Q，，只需证Q，由于Q显然成立，所以Q成立．综合法、分析法都是直接利用已知条件或定义、公理、定理等与所要证明的结论之间的关系推导出所要证明的结论或寻求出使它成立的充分条件，故均属于直接证法.2.反证法是间接证明的一种基本方法.对于某些看来明显成立而又不便知道根据什么去推导（综合法），甚至难于寻求到使之成立的充分条件（分析法）的“疑难”证明题，一般地，可在假设原命题不成立的前提下，经过正确的逻辑推理，最后得出矛盾，因此说明假设错误，从而证明了原命题成立.这种证明方法叫做反证法.简易逻辑部分中四种命题间的关系领悟得好的同学不难悟出反证法的原理不外乎“互为逆否命题的两个命题真假一致”，即：“P Q⇒”⇔“Q P⌝⇒⌝”．用反证法证题的格式一般为：假设Q不成立，若()Q⌝，，则p⌝，这与已知P（定义、公理、定理等）相矛盾，∴假设()Q⌝不成立，Q∴成立．1．综合法的每一步都是三段论（或其简略形式），大前提一定要正确，否则证明易出错.2.使用分析法时一定要注意对所要证明的结论是以“分析”的语气对待的，因而证明格式上应体现出“分析”探讨性（“要证…，只需证…”），而非直接肯定结论.四、直接证明与间接证明典型例题例3求证3725+<．错证：3725+<∵，22(37)(25)+<∴，1022120+<∴，215<∴，2125<∴，显然原不等式成立．错因：对分析法的原理不理解，以至于将所要证明的结论当成已知条件来用了.正：只需将“∵”改为“要证”，“∴”改为“只需证”.3.综合法和分析法往往不是单一地使用的，而是结合兼用的，特别是较为复杂的证明（教科书99P例3）.一般是先用综合法由已知条件P推出一个中间结论M，再用分析法探求，发现M正是使所要证结论Q成立的充分条件.证明过程用框图1表示；或者先用分析法寻求出使所要证明的结论Q成立的充分条件M，再用综合法由已知条件P推出M.证明过程用框图2表示.或例4 教科书中对99P例3的证法是先综合后分析，证明过程如框图１的形式；我们还可以改用框图2的形式，先分析后综合来证.证明：要证22221tan1tan1tan2(1tan)αβαβ--=++，只需证22222222sinsin11coscossin sin121cos cosβαβααβαβ--=⎛⎫++⎪⎝⎭，即证22221cos sin(cos sin)2ααββ-=-即证22112sin(12sin)2αβ-=-，即证224sin2sin1αβ-=③．另一方面，因为2(sin cos)2sin cos1θθθθ+-=，所以将已知中的①②代入上式，即得224sin2sin1αβ-=与③相同，于是问题得证．4.综合法与分析法当所用的证据相同时形式上是互逆的，因此往往可以互相改写，但须注意二者表达格式的迥异.5.反证法也经常与综合法或分析法结合使用.例5=只需证22≠，即证105，即证2125≠，而该式显然成立，≠不成等差数列．=2125≠∵，5≠，10∴，即3720+≠，即2≠，≠不成等差数列．。