五年级数学表面积和体积计算
- 格式:pdf
- 大小:670.50 KB
- 文档页数:8

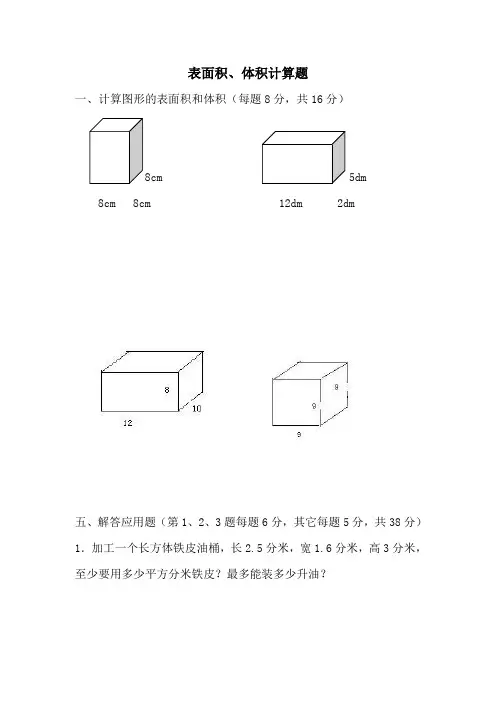
表面积、体积计算题
一、计算图形的表面积和体积(每题8分,共16分)
8cm 8cm 12dm 2dm
五、解答应用题(第1、2、3题每题6分,其它每题5分,共38分)1.加工一个长方体铁皮油桶,长2.5分米,宽1.6分米,高3分米,至少要用多少平方分米铁皮?最多能装多少升油?
2.学校要挖一个长方形状沙坑,长4米,宽2米,深0.4米,它占地多少平方米?需要挖出多少立方米的黄沙?
3.做一个棱长是6分米的正方形无盖鱼缸,需要玻璃多少平方分米?它的容积是多少升?
4.把一块棱长8厘米的正方体钢坯,锻造成长3.2分米,宽1分米的长方体钢板,这钢板有多厚?(损耗不计)
5.一个长方体机油桶,长8分米,宽2分米,高6分米.如果每升机油重720克,可装机油多少千克?
6.在一个长20m,宽8m,深1.6m的长方体蓄水池的底面和四周贴瓷砖,瓷砖是边长为2dm的正方形,贴完共需瓷砖多少块?
7.一个底面长和宽都是2分米的长方体玻璃容器,里面装有5升水,将一个铁球浸没在水中,这时水深 1.5分米。
这个铁球的体积是多少?。

体积与表面积的关系体积与表面积是几何学中的两个重要概念,它们在数学和物理学等领域中具有广泛的应用。
本文将探讨体积与表面积之间的关系,并分析其中的数学原理和物理应用。
一、体积的定义与计算公式体积是三维物体所占据的空间大小。
对于规则几何体,我们可以使用特定的公式来计算其体积:1. 正方体和长方体的体积公式:正方体的体积公式为V = a³,其中a表示正方体的边长。
长方体的体积公式为V = l × w × h,其中l、w和h分别表示长方体的长、宽和高。
2. 圆柱体和圆锥体的体积公式:圆柱体的体积公式为V = πr²h,其中r表示底面半径,h表示高度。
圆锥体的体积公式为V = (1/3)πr²h,其中r表示底面半径,h表示高度。
3. 球体的体积公式:球体的体积公式为V = (4/3)πr³,其中r表示球体的半径。
二、表面积的定义与计算公式表面积是三维物体外部所占据的面积大小。
同样地,对于规则几何体,我们可以使用特定的公式来计算其表面积:1. 正方体和长方体的表面积公式:正方体的表面积公式为A = 6a²,其中a表示正方体的边长。
长方体的表面积公式为A = 2lw + 2lh + 2wh,其中l、w和h分别表示长方体的长、宽和高。
2. 圆柱体和圆锥体的表面积公式:圆柱体的表面积公式为A = 2πr² + 2πrh,其中r表示底面半径,h表示高度。
圆锥体的表面积公式为A = πr² + πrl,其中r表示底面半径,l表示斜高线(母线)的长度。
3. 球体的表面积公式:球体的表面积公式为A = 4πr²,其中r表示球体的半径。
三、体积与表面积的关系体积和表面积之间存在一定的关系,特别是对于某些几何体而言。
以立方体为例,我们可以观察到体积和表面积之间的关系:对于边长为a的正方体来说,它的体积和表面积分别为V = a³、A = 6a²。

长方形的体积和表面积公式长方形是一种常见的几何形状,具有独特的性质和特征。
在数学中,长方形的体积和表面积是两个重要的指标,可以用来描述长方形的大小和几何特征。
我们来看一下长方形的体积公式。
体积是一个物体所占据的空间大小,对于长方形来说,它的体积可以通过长、宽和高来计算。
长方形的体积公式为:体积 = 长× 宽× 高。
其中,长方形的长代表长方形的一条边的长度,宽代表另一条边的长度,高则是长方形的高度。
通过这个公式,我们可以计算出长方形所占据的空间大小。
接下来,我们来看一下长方形的表面积公式。
表面积是一个物体外部所占据的空间大小,对于长方形来说,它的表面积可以通过长和宽来计算。
长方形的表面积公式为:表面积= 2 × (长× 宽 + 长× 高+ 宽× 高)。
其中,长方形的长和宽分别代表长方形的两条边的长度,高则是长方形的高度。
通过这个公式,我们可以计算出长方形外部所占据的空间大小。
长方形的体积和表面积公式是非常有用的,在很多实际问题中都可以应用到。
举个例子,假设我们有一个长方形的盒子,我们要知道这个盒子能够容纳多少东西,我们就可以通过计算盒子的体积来得到答案。
同样地,如果我们想要包裹这个盒子的表面需要多少纸张,我们可以通过计算盒子的表面积来得到答案。
除了计算长方形的体积和表面积,我们还可以利用这些公式来解决一些相关问题。
比如,如果我们知道长方形的体积和其中两个边的长度,我们可以通过这个信息来计算第三条边的长度。
这可以通过将体积公式稍作变形得到。
类似地,如果我们知道长方形的表面积和其中两个边的长度,我们也可以通过这个信息来计算第三条边的长度。
这可以通过将表面积公式稍作变形得到。
总结起来,长方形的体积和表面积公式是非常有用的数学工具,可以用来描述长方形的大小和几何特征。
通过这些公式,我们可以计算长方形所占据的空间大小,解决一些相关问题。
在实际应用中,我们可以利用这些公式来计算容器的容量、包装材料的需求量等等。


小学的各种数学公式之体积和表面积小学的各种数学公式之体积和表面积三角形的面积=底×高÷2。
公式s=a×h÷2正方形的面积=边长×边长公式s=a2长方形的面积=长×宽公式s=a×b平行四边形的面积=底×高公式s=a×h梯形的面积=(上底+下底)×高÷2公式s=(a+b)h÷2内角和:三角形的内角和=180度。
长方体的表面积=(长×宽+长×高+宽×高)×2公式:s=(a×b+a×c+b×c)×2正方体的表面积=棱长×棱长×6公式:s=6a2长方体的体积=长×宽×高公式:v=abh长方体(或正方体)的体积=底面积×高公式:v=abh正方体的体积=棱长×棱长×棱长公式:v=a3圆的周长=直径×π公式:l=πd=2πr圆的面积=半径×半径×π公式:s=πr2圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:s=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:s=ch+2s=ch+2πr2圆柱的体积:圆柱的体积等于底面积乘高。
公式:v=sh圆锥的体积=1/3底面×积高。
公式:v=1/3sh小学的各种数学公式之算术1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:a+b=b+a3、乘法交换律:a×b=b×a4、乘法结合律:a×b×c=a×(b×c)5、乘法分配律:a×b+a×c=a×b+c6、除法的性质:a÷b÷c=a÷(b×c)7、除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。

体积和表面积的关系与运算一、体积与表面积的定义1.体积:物体所占空间的大小。
2.表面积:物体表面的总面积。
二、体积与表面积的计算公式1.立方体的体积公式:V = a³(a为立方体的边长)2.立方体的表面积公式:S = 6a²三、体积与表面积的运算关系1.体积与边长的关系:体积随边长的增加而增加。
2.表面积与边长的关系:表面积随边长的增加而增加。
四、体积与表面积的单位1.体积的单位:立方米(m³)、立方分米(dm³)、立方厘米(cm³)等。
2.表面积的单位:平方米(m²)、平方分米(dm²)、平方厘米(cm²)等。
五、体积与表面积的换算1.1立方米(m³)= 1000立方分米(dm³)2.1立方米(m³)= 1000000立方厘米(cm³)3.1平方米(m²)= 100平方分米(dm²)4.1平方米(m²)= 10000平方厘米(cm²)六、常见几何体的体积与表面积公式1.圆柱体的体积公式:V = πr²h(r为圆柱的底面半径,h为圆柱的高)2.圆柱体的表面积公式:S = 2πrh + 2πr²3.圆锥体的体积公式:V = (1/3)πr²h(r为圆锥的底面半径,h为圆锥的高)4.圆锥体的表面积公式:S = πr² + πrl(l为圆锥的母线长)5.球的体积公式:V = (4/3)πr³(r为球的半径)6.球的表面积公式:S = 4πr²七、体积与表面积的实际应用1.计算物体的体积和表面积,以便了解物体的大小和形状。
2.在制作和包装物体时,计算体积和表面积,以节省材料和空间。
3.在建筑设计中,计算建筑物的体积和表面积,以确定建筑材料的需求量和建筑物的外观。
八、体积与表面积的拓展1.立体图形的体积和表面积的计算。

五年级下册数学关于体积,表面积横截面积1.一个长方体的铁皮水箱,长和宽都是2.5dm,深6dm。
做这样一个水箱,至少需要铁皮多少平方分米?(水箱有盖)2.一个长方体罐头盒,底面长13cm、宽7cm,高8.5cm。
如果在盒的四周贴上商标纸(上、下面不贴),这张商标纸的面积至少多少平方厘米?3.五年级同学向贫困地区捐款。
小刚把一个长50cm、宽40cm、高24cm的长方体纸箱各面都贴上了红纸作为捐款箱,除去上面捐款口的面积为350c㎡。
至少需要多少平方分米的红纸?4.一个长方体包裹,它的长、宽、高分别是4dm、3dm、2dm。
如果实际用纸是表面积的1.4倍,包装这个包裹至少要用多少平方分米的包装纸?5.一个房间长6m、宽3.5m、高3m,门窗面积是8㎡。
现在要把这个房间的四壁和顶面粉刷水泥漆。
如果每平方米需要水泥漆0.4kg,一共需要多少千克水泥漆?6.一个机器零件(如下图),要在它的前后两个面涂上红色防锈漆,其他漏出的面(底面不涂)涂上灰色防锈漆,涂红色防锈漆和灰色防锈漆的面积各是多少?7.一块正方体木料的棱长是40cm。
这块木料的表面积是多少平方厘米?8.求体积:修路队要给一段长150m、宽20m的水泥路面铺一层5cm厚的沥青,一共需要沥青多少立方米?9.一块正方体木料的棱长是40cm。
这块木料的体积是多少立方厘米?10.爸爸买回一块长方体形状的面包,面包长3dm、宽8cm、高5cm。
爸爸想把它平均分成5个长方体形状的小面包给五人,每个人分到面包的体积是多少立方厘米?11.王大爷家要用砖砌一段长20m、宽25cm、高2.8m的院墙。
如果每立方米用砖500块,砌这段院墙一共要用多少块砖?。

长方体和正方体的表面积、体积[教学内容]:五年级下册第三单元“长方体和正方体的表面积、体积”[教学目标]:知识技能:会解决有关长方体、正方体表面积体积计算的实际问题。
数学思考:1、通过探究、观察、比较等方法,进一步培养和提高灵活运用公式的能力及计算能力。
2、通过探究长方体和正方体表面积的变化关系,培养学生分析、解决问题的能力,以及良好的思维品质。
3、培养学生初步的空间观念、逻辑思维能力、动手操作能力。
问题思考:1、尝试从日常生活中发现并提出有关长方体和立方体表面积的数学问题,并加以解决。
2、经历与他人合作交流解决问题的过程,尝试解释自己的思考过程。
情感态度:通过用讨论、交流等学习方式,增强合作意识,提高学习能力。
[教学重点和难点]:教学重点:会解决有关长方体、正方体表面积体积计算的实际问题。
教学难点:提高灵活运用公式的能力及计算能力。
[教学准备]:12块棱长是1分米的正方体木块第一课时教学过程:和同学们再来重温一下幼儿园的活动,玩一回搭积木,只不过这一次要用我们学过的知识来解决搭积木中遇到的问题。
二、教学新课出示例题,教学 例1:第一组的小伙伴们拿出12块棱长是1分米的正方体木块,问大家:“用这12块棱长是1分米的正方体木块可以摆成多少种不同的长方体?表面积最大是多少?最小是多少?” 教师拿出12块棱长是1分米的正方体木块 谈话: 佳一数学班强调的是协作学习,现在请大家在小组内用课前准备好的学具摆一摆,看看有多少种摆法? 2、小组合作,一个同学摆,另一个同学画图做记录。
完成下表:分组汇报,摆的结果。
出示解析:(展示四种情况)1×12 2×6 3×4 2×3×2 3、分组讨论:表面积最大是多少?最小是多少?你发现什么规律? 4、分组汇报(尽可能多找学生的发言)。
下一步出示:图形长(分米) 宽(分米) 高(分米)表面积(平方分米)学生动手操作,合作交流生:最大:12×1×4+1×1×2=50(平方分米)学生讨论发言。

完整版)五年级下册数学表面积和体积练习题1、计算长方体钢材重量:长2米,横截面是边长为5厘米的正方形,每立方分米钢重7.8千克。
首先计算出长方体的体积为2m × 0.05m × 0.05m = 0.005立方米,然后将体积乘以钢的密度7.8千克/立方分米,得到钢材重量为0.005 × 7.8 =0.039千克。
2、一个棱长为5分米的正方体鱼缸,里面装满水,将水倒入一个底面积为48平方分米,高为6分米的长方体鱼缸里,求水深。
首先计算出正方体鱼缸的体积为0.05m × 0.05m ×0.05m = 0.立方米,然后将体积乘以水的密度1千克/立方分米,得到水的质量为0. × 1000 = 0.125千克。
将水倒入长方体鱼缸后,长方体鱼缸的底面积为48平方分米,高度为6分米,因此长方体鱼缸的体积为0.48立方米。
根据相似三角形的性质,可以得出两个鱼缸中水深的比例为5:12,因此水深为6分米 ×5/12 = 2.5分米。
3、将一块棱长为8厘米的正方体钢坯锻造成长16厘米,宽5厘米的长方体钢板,求钢板的厚度。
由于锻造过程中损耗不计,因此钢坯的体积等于钢板的体积。
钢坯的体积为0.008立方米,钢板的体积为0.016m × 0.05m × h,其中h为钢板的厚度。
将两式相等,解得h=0.16厘米。
4、一个长方形铁皮长30cm,宽25cm,从四个角各切掉一个长为5cm的正方形,然后做成一个无盖的盒子,求铁皮的面积和盒子的容积。
首先计算出四个正方形的面积为4 ×0.05m × 0.05m = 0.01平方米,然后将这个面积从原来的长方形铁皮面积中减去,得到剩余的面积为0.75平方米。
这个面积即为盒子的表面积。
盒子的容积为(30cm-2×5cm)×(25cm-2×5cm)×5cm=2500立方厘米=0.0025立方米。

五年级数学表面积和体积的题一、题目。
1. 一个正方体的棱长为5厘米,求它的表面积和体积。
- 解析:- 正方体表面积公式为S = 6a^2(a为棱长),这里a = 5厘米,所以表面积S=6×5^2=6×25 = 150平方厘米。
- 正方体体积公式为V=a^3,所以体积V = 5^3=125立方厘米。
2. 一个长方体,长为8厘米,宽为6厘米,高为4厘米,求它的表面积和体积。
- 解析:- 长方体表面积公式S=(ab + ah+bh)×2(a为长,b为宽,h为高),这里a = 8厘米,b = 6厘米,h = 4厘米。
则S=(8×6 + 8×4+6×4)×2=(48 + 32+24)×2=(80 + 24)×2 = 104×2=208平方厘米。
- 长方体体积公式V=abh,所以体积V=8×6×4 = 192立方厘米。
3. 一个正方体的表面积是216平方厘米,求它的棱长和体积。
- 解析:- 设正方体棱长为a,由正方体表面积公式S = 6a^2,已知S = 216平方厘米,则6a^2=216,a^2=36,解得a = 6厘米。
- 正方体体积公式V=a^3,所以体积V = 6^3=216立方厘米。
4. 一个长方体的体积是360立方厘米,长是10厘米,宽是6厘米,求它的高和表面积。
- 解析:- 由长方体体积公式V = abh,已知V = 360立方厘米,a = 10厘米,b = 6厘米,则h=(V)/(ab)=(360)/(10×6)=6厘米。
- 长方体表面积公式S=(ab + ah+bh)×2=(10×6+10×6 + 6×6)×2=(60+60 + 36)×2=(120+36)×2 = 156×2 = 312平方厘米。
体积与表面积的计算知识点总结在数学和物理学中,体积和表面积是基础的计算概念。
体积是指一个物体所占据的空间大小,而表面积则描述了物体外部的相对大小。
这两个概念在科学和实际生活中都具有重要的应用。
本文将总结体积与表面积的计算知识点,以帮助读者更好地理解和运用这些概念。
一、体积的计算体积的计算方法因不同几何体而异。
下面将根据常见几何体的形状介绍其体积的计算方法。
1. 立方体与长方体立方体和长方体是最基本的几何体,它们的体积计算非常简单。
立方体的体积等于边长的立方,公式为V = a³,其中V表示体积,a表示边长。
而长方体的体积则是长度、宽度和高度的乘积,公式为V = l ×w × h,其中l、w和h分别表示长度、宽度和高度。
2. 圆柱体圆柱体的体积计算需要利用底面积和高度。
底面积可通过圆的面积公式计算得出,即A = πr²,其中π为圆周率,r为底面半径。
再将底面积乘以高度h,即可得到圆柱体的体积,公式为V = A × h = πr²h。
3. 圆锥体与圆柱体类似,圆锥体的体积计算也需要利用到底面积和高度。
底面积仍然为A = πr²,而圆锥体的体积等于底面积乘以高度再除以3,公式为V = A × h / 3 = πr²h / 3。
4. 球体球体的体积计算相对复杂一些。
球体的体积等于4/3乘以π与半径r 的立方的乘积,公式为V = (4/3) × πr³。
这个公式是由球的表面积公式导出的。
二、表面积的计算与体积类似,不同几何体的表面积计算方法也不同。
下面将介绍几种常见几何体的表面积计算方法。
1. 立方体与长方体立方体和长方体的表面积计算比较简单,可以根据各个面的尺寸进行求和。
立方体的表面积等于6倍的边长的平方,公式为A = 6a²,其中A表示表面积,a表示边长。
而长方体的表面积等于2倍的长×宽加上2倍的长×高加上2倍的宽×高,公式为A = 2lw + 2lh + 2wh,其中l、w和h分别表示长度、宽度和高度。
完整版)小学生五年级表面积体积计算应用题1、计算长方体铁皮烟囱的表面积:2.5dm x 2m x 2 +1.6dm x 2m x 2 +2.5dm x 1.6dm x 2 = 22.4平方分米。
2、计算沙坑的体积:4m x 2m x 0.4m = 3.2立方米。
需要填满沙坑,所以需要3.2立方米的黄沙。
3、根据体积不变的原则,计算钢板的体积:8cm x 8cm x 8cm = 512立方厘米。
将其转化为长方体钢板的体积:16cm x5cm x h = 512立方厘米,解得h=16cm。
所以钢板的厚度是16cm。
4、计算机油桶的容积:8dm x 2dm x 6dm = 96升。
所以可以装96升 x 0.72千克/升 = 69.12千克机油。
5、计算纸盒的容积:12cm x 4cm x 5cm = 240立方厘米。
小立方体的容积为2cm x 2cm x 2cm = 8立方厘米。
所以最多可以容纳240立方厘米/8立方厘米 = 30个小立方体。
6、正方体水箱的容积为4dm x 4dm x 4dm = 64立方分米。
将其倒入长方体水箱中,长8dm,宽2.5dm,高h,容积为8dm x 2.5dm x h = 20立方分米。
解得h=3.2dm,所以水深为3.2dm。
7、计算底面边长:24cm/4 = 6cm。
底面面积为6cm x 6cm = 36平方厘米。
所以体积为36平方厘米 x 10cm = 360立方厘米。
8、计算铺地的面积:60m x 40m = 2400平方米。
所以可以铺240立方米/2400平方米 = 0.1米 = 10厘米厚的土。
9、(1)计算玻璃鱼缸的表面积:2 x 12dm x 5dm + 2 x12dm x 6dm + 2 x 5dm x 6dm = 312平方分米。
所以制作这个玻璃鱼缸至少需要312平方分米的玻璃。
(2)计算水的体积:12dm x 5dm x (6dm-1dm) = 240立方分米。
长方体的棱长和=(长+宽+高)x4正方体的棱长和=棱长x12长方体的表面积=(长x宽+长x高+宽x高)x2正方体的表面积=棱长x棱长x6长方体的体积=长x宽x高正方体的体积=棱长x棱长x棱长长方体的体积(正方体的体积)=底面积×高三角形的面积=底x高÷21、一个面的面积是36平方米的正方体,它所有的棱长的和是多少厘米?2、用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?3.天天游泳池,长25米,宽10米,深米,在游泳池的四周和池底砌瓷砖,如果瓷砖的边长是1分米的正方形,那么至少需要这种瓷砖多少块?4、把棱长12厘米的正方体切割成棱长是3厘米的小正方体,可以切割成多少块?5、把一个棱长15分米的正方体木块,平均分成三个长方体后,木块的表面积增加多少方厘米?6、一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是多少平方厘米?1、制做一个无盖的长方体鱼缸,长米,宽米,高米,制做这样一个鱼缸至少需要玻璃多少平方米?2、一块长米,宽6分米,厚3分米的长方体木块,可以截出多少块棱长为3分米的正方体?3、一个长方体,如果高增加3厘米,就成为一个正方体。
这时表面积比原来增加了96平方厘米。
原来的长方体的体积是多少立方厘米?4、把一个棱长6分米的正方体钢锭熔铸成一个长方体钢锭,这个长方体长9分米,宽4分米,求这个长方体钢锭高多少分米?5、一节烟囱长1米,口径是一个正方形,边长是2分米,做6个这样的烟囱要多少平方米的铁皮?1、一个长方体的棱长总和是80厘米,长10厘米,宽是7厘米。
高是多少厘米?表面积?2、一个长方体的长是10厘米,宽是8厘米,高是2厘米,这个长方体的棱长之和是多少厘米?表面积是多少?体积是多少?3、一根长96厘米的铁丝围成一个正方体,这个正方体的棱长是多少厘米?表面积?4、学校要修长50米,宽42米,的长方形操场。
小学五年级数学几何图形周长、面积、体积计算公式大全长方形、正方形的周长和面积公式:长方形的周长=(长+宽)×2 C=(a+b)×2正方形的周长=边长×4 C=4a长方形的面积=长×宽S=ab正方形的面积=边长×边长S=a·a= a2三角形、平行四边形、梯形的面积公式:三角形的面积=底×高÷2 S=ah÷2平行四边形的面积=底×高S=ah梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2圆的周长和面积公式:圆的周长=直径×π公式:L=πd=2πr圆的面积=半径×半径×π公式:S=πr2圆柱的侧面积和表面积公式:圆柱的侧面积:圆柱的侧面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2圆柱圆锥的体积公式:圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
公式:V=1/3Sh分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
分数的乘法则:用分子的积做分子,用分母的积做分母。
分数的除法则:除以一个数等于乘以这个数的倒数。
一、周长公式1. 长方形的周长=(长宽)×22. 正方形的周长=边长×43. (重点)圆的周长=圆周率×直径= 2×圆周率×半径二、面积公式1. 长方形的面积=长×宽2. 正方形的面积=边长×边长3. 三角形的面积=底×高÷24. 平行四边形的面积=底×高5. 梯形的面积=(上底下底)×高÷26. (重点)圆的面积=圆周率×半径27. (重点)圆柱的侧面积:圆柱的侧面积等于底面的周长乘高。
体积和表面积的计算及应用一、体积的计算1.体积的定义:物体所占空间的大小叫做物体的体积。
2.体积的单位:立方米(m³)、立方分米(dm³)、立方厘米(cm³)等。
3.常见几何体的体积公式:–立方体:V = a³(a为边长)–长方体:V = lwh(l为长,w为宽,h为高)–正方体:V = a³(a为边长)–圆柱体:V = πr²h(r为底面半径,h为高)–圆锥体:V = 1/3πr²h(r为底面半径,h为高)4.体积的计算在生活中的应用:如计算物体的容量、容积等。
二、表面积的计算1.表面积的定义:物体所有面的总面积叫做物体的表面积。
2.表面积的单位:平方米(m²)、平方分米(dm²)、平方厘米(cm²)等。
3.常见几何体的表面积公式:–立方体:S = 6a²(a为边长)–长方体:S = 2lw + 2lh + 2wh(l为长,w为宽,h为高)–正方体:S = 6a²(a为边长)–圆柱体:S = 2πrh + 2πr²(r为底面半径,h为高)–圆锥体:S = πr² + πrl(r为底面半径,l为斜高)4.表面积的计算在生活中的应用:如计算物体的表面积、制作物体的包装等。
三、体积和表面积的应用1.计算物体的体积和表面积,可以了解物体的空间大小和外表形状。
2.在生活中,计算物体的体积和表面积,可以帮助我们更好地利用空间,提高生活和工作效率。
3.体积和表面积的计算,可以帮助我们解决一些实际问题,如制作物体模型、设计建筑物的结构等。
4.体积和表面积的计算,是数学在实际生活中的重要应用,有助于培养学生的空间想象能力和实际应用能力。
以上就是关于体积和表面积的计算及应用的知识点总结,希望对你有所帮助。
在学习过程中,要注意理论联系实际,提高自己的空间想象能力和实际应用能力。