长方形和正方形的面积和周长的复习
- 格式:doc
- 大小:66.50 KB
- 文档页数:4

小学三年级长方形和正方形周长面积知识点一、知识的回顾1.物体的表面或封闭图形的大小,就是他们的面积。
2.比较两个图形面积的大小,要用统一的面积单位来测量。
3.常用的面积单位有平方厘米、平方分米、平方米。
4.常用的长度单位有厘米、分米、米。
5.边长1厘米的正方形面积是1平方厘米。
6.边长1分米的正方形面积是1平方分米。
7.边长1米的正方形面积是1平方米。
8.长方形的面积=长×宽正方形的面积=边长×边长9.长方形的周长=(长+宽)×2正方形的周长=边长×4正方形的边长=周长÷4 10.相邻的两个常用的长度单位间的进率是10。
11.相邻的两个常用的面积单位间的进率是100。
12.1平方米=100平方分米;1平方分米=100平方厘米;注:面积和周长是不能相比较的。
二、基础练习1、在()里填上“>”“<”或“=”。
19平方米()230平方厘米340平方分米()35平方米500平方分米()5平方米40平方米()400平方厘米70平方分米()7平方米500平方厘米()60平方分米80平方分米()1平方米3600平方厘米()360平方米2、400平方分米=()平方米5平方分米=()平方厘米300平方厘米=()平方分米300米=()分米420分米=()米24平方米=()平方厘米3平方米=()平方分米=()平方厘米三、应用题计算1、一个长方形的周长是64米,宽为8米,它的长是多少米?它的面积是多少平方米?2、一根铁丝长80厘米,做成一个正方形的铁丝框,它的面积是多少厘米?3、人行道长180米,宽3米,要在上面铺石砖,如果每铺9平方米需要6元,铺完这条人行道一共需要多少钱?。

1、长方形的面积=【】,正方形的面积=【】长方形的周长=【】,正方形周长=【】正方形的边长=【】长方形长=【 2个】长方形的宽= 【 2个】2、用一根铁丝或绳子做成长方形或者正方形【】相同,【】不同,【】的面积大。
3、一根40厘米的铁丝做成正方形,面积是【】4、周长16米的正方形,面积是【】5、长方形里做最大的正方形,【】是正方形的边长6、长15米,宽8米的长方形做成一个最大的正方形,正方形的面积是【】,剩下的面积是【】,剩下图形的周长【】7、用小正方形摆出不同的形状,【】一样,【】不一样8、用11个边长1分米小正方体摆出不重叠的形状,面积都是【】。
9、两个长方形的周长相等,面积【】10、两个长方形的面积相等,周长【】11、两个正方形的面积相等,周长【】12、两个正方形的周长相等,面积【】13、至少【】个小正方形能拼成一个大正方形。
14、边长5米的正方形,边长增加2米,面积增加【】平方米15、周长一样的长方形和正方形【】的面积大16、一辆清洁车平均每分钟行驶100米,扫过的路面的宽是3米,清洁车行驶8分钟,扫过的面积是【】17、一面镜子长3米,宽2米,这块镜子有多大?如果给镜子镶上边框,边框的长是多少?18、一块菜地,长15米,宽4米,要给菜地围篱笆,需要多长?如果每平方米种5棵花,这块地能种多少棵花?19、长方形果园长20米,宽3米,如果每5平方米种一棵树,一共种多少棵树?20、边长4米的正方形,周长和面积一样大【判断对错原因】边长10分米的正方形,周长4米【判断对错原因】21、【】正方形面积是1平方厘米【】正方形面积是1平方分米【】正方形面积是1平方米22、纽扣的面积是2 【】,成人一个手掌的面积1【】一张报纸的面积是35【】,黑板面积3【】教室门高2 【】,电脑屏幕的面积【】百元钞票的面积120【】小明家的新房130 【】大楼高30【】小红的身高140【】23、12〖16个、18个〗个小正方体能摆成【】个不同的长方体,方法是【】24、长50米宽30米的长方形菜地中有一个边长8米的正方形,菜地的面积是【】25、足球场长95米,宽60米,小明跑了两圈能跑多少米?26、一根铁丝做成长方形长是11cm,宽是7cm,把它改成一个正方形,正方形的面积是多少?27、菊花园长24米,宽20米,每平方米种8棵菊花,一共可以种多少课菊花?如果每5平方米施肥一千克,一共要多少千克肥料?28、一块正方形的菜园,有一面靠墙,用24米的篱笆围起来,这块菜地的边长是多少?面积是多少?29、一块长方形菜地,一面靠墙,长是22米,三面用40米的篱笆围了起来。

长方形和正方形的面积和周长长方形和正方形是几何学中常见的两类四边形。
它们的面积和周长是计算其重要属性的基本公式。
本文将重点介绍长方形和正方形的面积和周长的计算方法,并探讨它们在实际生活中的应用。
一、长方形的面积和周长长方形是一种具有四个直角的四边形,相邻的两条边长度不相等。
为了计算长方形的面积和周长,我们需要知道其两条相邻边的长度。
1. 长方形的面积长方形的面积是指该图形所围成的区域的大小。
面积的计算公式为:面积 = 长 ×宽。
例如,如果长方形的长为5米,宽为3米,那么它的面积可以计算为:5 × 3 = 15平方米。
因此,该长方形的面积为15平方米。
2. 长方形的周长长方形的周长是指长方形的四条边的总长度。
周长的计算公式为:周长 = 2 × (长 + 宽)。
继续以前述长方形为例,长方形的长为5米,宽为3米,那么它的周长可以计算为:2 ×(5 + 3) = 16米。
因此,该长方形的周长为16米。
二、正方形的面积和周长正方形是一种具有四个直角且四条边长度相等的四边形。
为了计算正方形的面积和周长,我们只需要知道其一条边的长度。
1. 正方形的面积正方形的面积是指该图形所围成的区域的大小。
面积的计算公式为:面积 = 边长 ×边长,也可以简写为面积 = 边长^2。
例如,如果正方形的边长为4厘米,那么它的面积可以计算为:4 ×4 = 16平方厘米。
因此,该正方形的面积为16平方厘米。
2. 正方形的周长正方形的周长是指正方形的四条边的总长度。
周长的计算公式为:周长 = 边长 × 4,即周长等于边长的四倍。
继续以前述正方形为例,正方形的边长为4厘米,那么它的周长可以计算为:4 × 4 = 16厘米。
因此,该正方形的周长为16厘米。
三、长方形和正方形的应用长方形和正方形的面积和周长在日常生活和工作中有广泛的应用。
以下是一些例子:1. 房屋面积和周长计算在房屋建设和装修过程中,长方形和正方形的面积和周长的计算经常被用来确定墙壁、地板和天花板的面积,从而确定装修材料的用量。
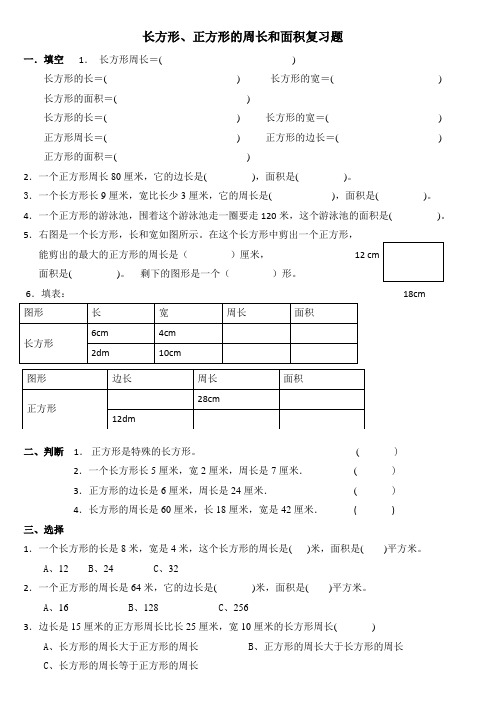
长方形、正方形的周长和面积复习题一.填空1.长方形周长=()长方形的长=() 长方形的宽=() 长方形的面积=()长方形的长=() 长方形的宽=() 正方形周长=() 正方形的边长=() 正方形的面积=()2.一个正方形周长80厘米,它的边长是(),面积是()。
3.一个长方形长9厘米,宽比长少3厘米,它的周长是(),面积是()。
4.一个正方形的游泳池,围着这个游泳池走一圈要走120米,这个游泳池的面积是()。
5.右图是一个长方形,长和宽如图所示。
在这个长方形中剪出一个正方形,能剪出的最大的正方形的周长是()厘米,面积是()。
剩下的图形是一个()形。
6.填表:18cm二、判断1.正方形是特殊的长方形。
( )2.一个长方形长5厘米,宽2厘米,周长是7厘米.( )3.正方形的边长是6厘米,周长是24厘米.( )4.长方形的周长是60厘米,长18厘米,宽是42厘米.()三、选择1.一个长方形的长是8米,宽是4米,这个长方形的周长是()米,面积是()平方米。
A、12B、24C、322.一个正方形的周长是64米,它的边长是()米,面积是()平方米。
A、16B、128C、2563.边长是15厘米的正方形周长比长25厘米,宽10厘米的长方形周长()4、一个正方形剪成2个长方形后,两个长方形的周长和()原来正方形的周长。
A、相等B、大于C、小于四.计算下面图形的周长和面积12cm 10dm五、解决问题1.一块长方形菜地,长18米,宽9米,一面靠墙(如下图),其它三面墙围上竹篱笆。
竹篱笆长多少米?菜地的面积时多少平方米?2.一个长方形操场,长是100米,宽40米,这个操场的面积是多少平方米?围着这个操场跑两圈,要跑多少米?3.一段长60厘米的铁丝围成一个最大的正方形,这个正方形的边长是多少厘米?面积时多少平方厘米?4.一个长方形和一个正方形的周长相等.长方形的长为12米,宽为8米,那么正方形的面积是多少平方米?5.长方形的长16分米,长是宽的2倍,周长是多少分米?6.把两个完全相同的长方形拼在一起,原来长方形的长是4厘米,宽是2厘米。

长方形和正方形的面积与周长知识点长方形和正方形是几何学中常见的两种形状,它们有不同的特点和性质。
本文将详细介绍长方形和正方形的面积与周长的计算方法以及相关知识点。
1. 长方形的面积与周长长方形是指拥有两对相等且平行的边的四边形。
其中,相邻边长度不同的称为长和宽,长和宽的度量单位一致。
长方形的面积即为长乘以宽,周长则是长和宽的两倍之和。
设长方形的长为L,宽为W,则长方形的面积S为 S = L * W,周长P为 P = 2 * (L + W)。
这是长方形面积与周长的基本计算公式。
2. 正方形的面积与周长正方形是一种特殊的长方形,它的四条边长度相等且每个角都为直角。
正方形的边长通常用a表示。
正方形的面积即为边长的平方,周长则是边长的四倍。
设正方形的边长为a,则正方形的面积S为S = a^2,周长P为P = 4a。
这是正方形面积与周长的基本计算公式。
3. 长方形和正方形的性质比较长方形和正方形面积与周长的计算方法不同,下面将对它们的性质进行比较。
(1)面积比较:相同周长下,正方形的面积最大。
这是因为正方形的四条边长度相等,而长方形的两条边可以有不同的长度,因此,给定周长情况下,正方形的边长最大,面积最大。
(2)周长比较:相同面积下,正方形的周长最小。
这是因为正方形的边长相等,而长方形的两条边可以有不同的长度,给定面积情况下,正方形的边长最小,周长最小。
综上所述,长方形和正方形在面积与周长上有不同的特点和计算方法。
在实际应用中,我们常常需要根据给定的条件计算长方形或正方形的面积和周长,以便解决相关问题。
例如,假设一块土地的形状是长方形,已知它的周长为40米,我们可以利用周长的计算方法求出长为10米。
如果要计算这块土地的面积,可以利用面积的计算方法得到100平方米。
又如,假设一块地的形状是正方形,已知它的面积为64平方米,我们可以利用面积的计算方法求出边长为8米。
如果要计算这块地的周长,可以利用周长的计算方法得到32米。

苏教版三年级数学上册第三单元
《长方形和正方形》知识整理及典型练习
一、长方形和正方形的特征
二、什么是周长
沿着封闭..
图形的边线,从起点到起点的长度。
三、长方形和正方形周长计算的方法
1、计算下面图形的周长
注意:计算长方形的周长一般用第一种方法。
四、长方形的长或宽的求法,正方形边长的求法
1. 长方形的长宽和等于周长的一半。
长方形的周长÷2=长宽和(1条长和1条宽的长度)
长方形的长=周长÷2—宽 长方形的宽=周长÷2—长 2. 正方形的边长=周长÷4
五、长方形和正方形的画法
正方形有4个直角,有4条边,四条边都相等
1、长方形的画法
你能在方格纸上画出周长是20厘米的长方形或正方形吗?能画出不同的长方形吗?(每个小方格的边长表示1厘米)
2、正方形的画法
在方格纸上画周长20厘米的正方形
六、典型练习
1. 2. 3.
4.
5.
6.
10.用两个相同的长方形拼成了一个正方形,已知
正方形的周长是40厘米,每个长方形的周长是多
少厘米?
11把两个相同的长方形拼成了一个正方形,周长
减少了40厘米,每个长方形的周长是多少厘米?。
面积:( )平方厘米周长:()平方厘米周长:( )平方厘米面积:()平方厘米 三下《长方形和正方形的面积》单元复习题班级 姓名【复习准备】1.长方形的周长、面积计算公式:长方形的周长=(长+宽)×2 ; 长方形的面积=长×宽变形公式:长=周长÷2-宽 或 宽=周长÷2-长长=长方形的面积÷宽 或 宽=长方形的面积÷长2.正方形的周长、面积计算公式:正方形的周长=边长×4 ; 正方形的面积=边长×边长 变形公式:边长=正方形的周长÷4【复习例题】例1:(1)下图中每个小方格表示1平方厘米,你能说出每个图形的面积是多少平方厘米吗?(2)用面积为1平方厘米的正方形拼成下面的图形,它们的面积各是多少?它们的周长呢?例3:一个长方形游泳池,长25米,宽10米。
(1) 这个游泳池的占地面积是多少平方米?(2) 如果沿着池口走一圈,那么一共要走多少米?例4:一台压路机,每分钟前进15米,压过的宽度是2米。
压路机工作半小时可以压路面多少平方米?例5:将一个边长是12米的正方形花坛改造成一个长方形花坛,如果面积不变,改造后长方形花坛的宽是9米,那么改造后长方形花坛的长是多少米?例6:下图中每个小方格表示1平方厘米。
(1)在图中画一个面积是16平方厘米的正方形。
(2)再画一个与上述正方形面积相等的长方形。
(3)计算该长方形的周长。
例7:用24米长的篱笆(全部用完)一面靠墙围了一个正方形菜地,这块菜地的面积是多少平方米?也就是多少平方分米?(先画出草图,再列式计算)例8:一间客厅,用边长为6分米的正方形瓷砖铺地,需要50块。
(1)这间客厅的地面面积是多少平方分米?合多少平方米?(2)如果改用边长为3分米的地砖来铺,那么一共需要多少块地砖?例9:一个长方形的长是11厘米,宽是4厘米。
现要在这个长方形中剪最大的正方形。
(1)求剪得的最大正方形的面积是多少平方厘米?(2)最多能剪几个这样的正方形?(先在图中画一画,再回答)(3)把所有能剪的最大正方形都剪下后,剩下图形的面积是多少平方厘米?【复习练习】一.填空题。
长⽅形和正⽅形的⾯积知识归纳长⽅形和正⽅形的⾯积知识归纳1、⽐较两个图形⾯积的⼤⼩,要⽤统⼀的⾯积单位来测量。
2、常⽤的⾯积单位有平⽅厘⽶,平⽅分⽶、平⽅⽶。
填写⾯积单位可有三个参照物:⼤拇指指甲盖⼤约1平⽅厘⽶,成⼈⼿掌⾯积⼤约1平⽅分⽶,4个⼩朋友⼿拉⼿围成⼀个正⽅形⼤约1平⽅⽶。
3、边长1厘⽶的正⽅形⾯积是1平⽅厘⽶;边长1分⽶的正⽅形⾯积是1平⽅分⽶;边长1⽶的正⽅形⾯积是1平⽅⽶。
4、长⽅形:长⽅形的⾯积=长×宽长⽅形的周长=(长+宽)×2已知⾯积求长:长=长⽅形⾯积÷宽已知周长求长:长=长⽅形周长÷2-宽已知⾯积求宽:宽=长⽅形⾯积÷长已知周长求:宽=长⽅形周长÷2-长正⽅形:正⽅形的⾯积=边长×边长正⽅形的周长=边长×4已知⾯积求边长:边长=正⽅形⾯积÷边长已知周长求边长:边长=正⽅形周长÷45、相邻的两个常⽤的长度单位间的进率是10;相邻的两个常⽤的⾯积单位间的进率是100。
1平⽅⽶=100平⽅分⽶ 1平⽅分⽶=100平⽅厘⽶6、⾯积相等的长⽅形,周长不⼀定相等;周长相等的长⽅形,⾯积不⼀定相等。
注:⾯积和周长是不能相⽐较的;7、能正确进⾏⾯积单位间的换算:单位换算歌单位转换仔细瞧:低化⾼来很简单,除以进率记⼼间;⾼化低来并不难,乘进率时想周全。
8、铺地砖问题:①先算出所铺地⾯的总⾯积;②计算出每块地砖的⾯积;③将这两个⾯积统⼀成相同的⾯积单位;④地砖的总块数=所铺地⾯的总⾯积÷每块地砖的⾯积.9、刷墙的(有的中间有⿊板、窗户等):求要⽤到的⾯积等于⼤⾯积减去⼩⾯积10、⾯积相等的长⽅形、正⽅形中,长⽅形的周长最长;周长相等的长⽅形、正⽅形中,正⽅形⾯积最⼤。
长方形和正方形的面积和周长的复习
教学目标:
1、能熟练地进行长方形和正方形的面积和周长计算,比较灵活第运用长方形和正方形的面积和周长知识进行相关的变式练习的解答。
2、能根据具体的问题情境,选择相应的数学方法进行探究、实践,发现并解决问题。
3、通过举例、观察、发现等数学活动,把抽象的问题具体化,进而解决问题,促进思维的发展。
4、通过数学活动,让学生体验数学方法的妙处,树立学习数学的信心,激发学习数学的热情。
教学过程: 一、基础部分
1、引入:闭眼想象,一个点先向正北方移动,再向正东方移动,再向正南方移动,最后向正西方移动,回到原来的起点。
你想到了一个什么图形? 预设:长方形、正方形。
(想象是空间感培养的前提,通过想象学生脑中出现了长方形,这样为课堂教学铺平道路。
)
2、基础梳理。
(1)出示问题,自主解决。
① 多媒体演示,这就是你们想象的长方形。
你能求长方形的面积 和周长。
(不给出长和宽的长度)
预设:图中没有告诉长和宽的长度,没法计算。
师:那就是说解决这道题的必要信息不具备,计算长方形的周长和面积的必要条件是要知道长和宽的长度。
(复习课中的知识梳理的途径有很多,关键是唤起学生内心深处对知识与学法的回忆及整理。
让学生顿悟求周长的必要条件。
) ② 如右图:现在能求它的周长和面积了吗? 生独立计算,说出计算方法和依据和结果。
板书:长方形的周长=(长+宽)×2
(6+4)×2=20(厘米)
长方形的面积=长×宽 6×4=24(平方厘米)
(2)关联问题,自主探索。
如果在这个长方形中剪去一个最大的正方形,(你觉得该怎么剪?同桌讨论) ①正方形的周长和面积分别是多少? ②剩余部分的周长和面积分别是多少?
(学生先自主解答问题,同桌讨论,然后汇报交流。
)
问:在长方形中剪去最大的正方形,你是怎么做的?首先要确定什么?怎样计算? 生汇报,师板书:
正方形的周长=边长×4 4×4=16(厘米)
正方形面积=边长×边长 4×4=16(平方厘米)
剩余部分的周长: 先求宽,6-4=2(厘米) 周长:(4+2)×2=12(厘米) 6×2=12(厘米) (6+4) ×2=20(厘米)
4厘米
6厘米
面积:4×2=8(平方厘米)6×4—4×4=8(平方厘米)
(周长和面积是本节课学习的重点,教学中采取边练习边梳理的方式,既可以唤起学生的记忆,又巩固所学知识。
)
(3)对比观察,引发思考。
从上述周长和面积的结果中我们可以知道,在一个长方形中剪去一最大的正方形,面积减少了,剩余的周长可能有减少,也可能不变。
(复习课让学生主动参与到教学中,在探索中不断让思维走向深刻,本环节没有沿袭传统以练习训练的整理知识分的复习形式,而是一问题为载体,以探索的形式来验证数学思考,以达到解决问题的目的)
二、探索部分
第一层次:
1、问题引领,以探促练。
出示问题:如果从一个长方形中剪去一部分(长方形或正方形)后,你认为剩余部分的周长和原长方形周长相比,会有几种情况?
(1)独立思考。
(2)用画图的方式把你的想法表示出来。
(3)把你的想法和同桌交流讨论。
(学生探索后展示汇报)
预设:
①和原来的周长相等。
沿长方形的角剪去一部分(长方形或正方形)“破一角”
板书:周长不变———破一角
②比原来的周长长。
沿着长方形一条边剪去一部分(长方形或正方形)。
“破一边”
板书:周长增加———破一边。
③比原来的周长短。
(充分给予学生动手实践的机会,以此来说明自己的结论,这其实就是学生“悟”问题的过程,使学生的数学思考越来越深刻。
)
2、策略梳理,练习跟进。
(1)媒体出示,系统感知。
①长方形的面积减少,剩余部分的周长不变。
②长方形的面积减少,剩余部分的周长变大。
③长方形的面积减少,剩余部分的周长变小。
④长方形的面积减少,剩余部分的周长不变。
(数学知识的学习总是从零散到系统的过程,这个过程需要借助辨析,观察、概括与整理等活动。
本环节让学生先独立思考交流汇报,在通过媒体演示,进一步引导学生梳理解题策略,为学习质量的提升成为可能)
(2)练习反馈,整体跟进。
说一说:如果要计算下列图形的周长,至少需要量出几条边的长度?
第二层次:
1、 问题驱动,以例悟道。
出示:
6×4=24(平方厘米) 如果长方形的面积相等,那么他们的周长一定相等吗? 生思考回答:不一定。
请举例说明.
(长方形的面积相等,周长是否相等或存在什么规律性联系呢?破解这个结论性问题,需要教师引领学生“退”到简单处发现规律,所以列举法不失为一条捷径。
) 2、列举说明,验证结论。
(1)学生自主列举。
汇报。
(2)观察发现。
从上面的例子中,你发现了什么?
A 面积相同,周长是不一样的。
B 长和宽越接近,周长越小。
如果长方形和正方形的面积相等,那么谁的周长较小?
(归纳推理是学阶段主要的数学思想,符合儿童的认知规律。
这个环节先让学生列举,然后进行观察、发现规律,让学生经历变与不变的归纳过程,促进学生的思维的发展。
) 第三层次:
1、动手操作,探寻规律。
出示
你能在格子图中画出周长和这个长方形一样的长方形吗?画好后计算出它们的面积,从中你有发现了什么呢? 4厘米
6厘米4厘米6厘米
2、观察发现,总结规律。
(1)引导观察,发现内在联系。
(2)出示结论,揭示规律。
长方形和正方形和周长相等,正方形的面积大。
(用图形和数据来说明数学问题比较直观形象,学生容易接受。
尤其是这样规律性问题的探索与巩固,用以探带练的方式进行复习,容易激发学生的求知欲,对问题的认识会更深刻。
)3、概括总结,学法梳理。
当我们在学习中遇到一些结论性或规律性的问题时,有些淡忘了,该怎么办呢?
举例说明。
总结:我们可以通过“列举—观察---发现---- 结论”这样的途径来解决一些问题。
(学法形成需要引领经历与梳理的过程,让学生经历学法应用过程,最后进行一次集中整理,为学法形成起画龙点睛的作用。
)
4、实践练习,学法迁移。
(1)出示问题:把一个长方形剪成三个完全一样的正方形后,周长和比原来增加了20厘米。
原来长方形的面积是多少平方厘米?
(2)用一根铁丝围成一个边长为6厘米的正方形,如果把这根铁丝围成一个边长为8厘米的长方形,这个长方形的面积是多少平方厘米?
(2)一个正方形被平分成三个形状和大小一样的长方形,其中一个长方形的周长是24厘米,那么原来正方形的面积是多少平方厘米?。