两独立样本t检验

两独立样本T检验
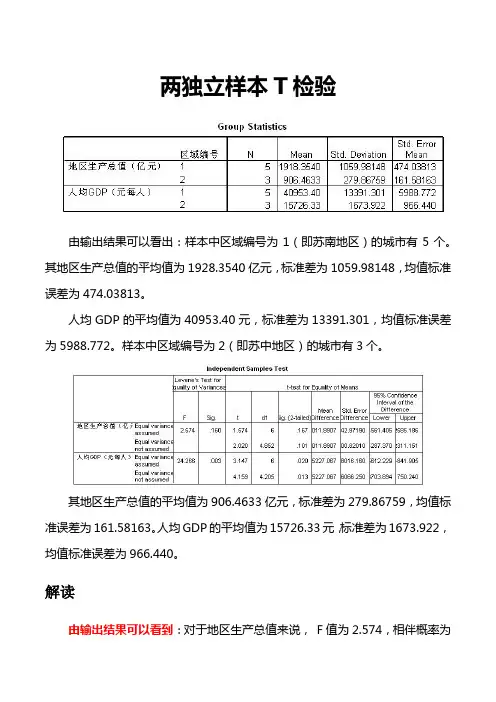
由输出结果可以看出：样本中区域编号为1（即苏南地区）的城市有5个。

其地区生产总值的平均值为1928.3540亿元，标准差为1059.98148，均值标准误差为474.03813。

人均GDP的平均值为40953.40元，标准差为13391.301，均值标准误差为5988.772。

样本中区域编号为2（即苏中地区）的城市有3个。

其地区生产总值的平均值为906.4633亿元，标准差为279.86759，均值标准误差为161.58163。

人均GDP的平均值为15726.33元，标准差为1673.922，均值标准误差为966.440。

解读
由输出结果可以看到：对于地区生产总值来说，F值为2.574，相伴概率为
0.160，大于显著性水平0.05，不能拒绝方差相等的假设，可以认为苏南和苏中的地区生产总值方差无显著差异；然后看方差相等时T检验的结果，T统计量的相伴概率为0.167，大于显著性水平0.05，不能拒绝T检验的零假设，也就是说，苏南和苏中两个地区城市生产总值平均值不存在显著差异。

另外从样本的均值差的95%置信区间看，区间跨0，这也说明两个地区生城市生产总值的平均值无显著差异。

对于人均GDP来说，F值为24.266，相伴概率为0.003，小于显著性水平0.05，拒绝方差相等的假设，可以认为苏南和苏中地区城市人均GDP方差存在显著差异；然后看方差不相等时T检验的结果，T统计量的相伴概率为0.013小于显著性水平0.05，拒绝T检验的零假设，也就是说，苏南和苏中两个地区城市人均GDP平均值存在显著差异。

另外从样本的均值差的95%置信区间看，区间没有跨0，这也说明两个地区城市人均GDP平均值存在显著差异。

两样本t检验计算公式1.对于两个独立样本的t检验：t=(x1-x2)/√(s1^2/n1+s2^2/n2)其中t表示t值；x1和x2分别表示两个样本的均值；s1和s2分别表示两个样本的标准差；n1和n2分别表示两个样本的样本容量。

2.对于两个相关样本的t检验：t = (x1 - x2) / (sdiff / √n)其中t表示t值；x1和x2分别表示两个样本的均值差；sdiff表示两个样本的均值差的标准差；n表示样本容量。

接下来，我们将具体介绍两个不同情况下的两样本t检验计算过程。

一、独立样本t检验计算过程：1.收集两个样本的数据并计算样本均值和样本标准差；2.计算两个样本的样本容量；3.计算两个样本的方差；4.根据计算得到的数据，带入公式计算t值；5.查表或使用统计软件计算得到的t值对应的P值；6.对比P值与设定的显著性水平（通常为0.05），如果P值小于显著性水平，则可以拒绝原假设，即认为样本均值存在显著差异；反之，接受原假设，即认为样本均值不存在显著差异。

二、相关样本t检验计算过程：1.收集两个样本的相关数据并计算样本均值差；2.计算样本均值差的标准差；3.计算样本容量；4.根据计算得到的数据，带入公式计算t值；5.查表或使用统计软件计算得到的t值对应的P值；6.对比P值与设定的显著性水平（通常为0.05），如果P值小于显著性水平，则可以拒绝原假设，即认为样本均值存在显著差异；反之，接受原假设，即认为样本均值不存在显著差异。

需要注意的是，在进行两样本t检验前，需要满足以下前提条件：1.数据来自正态分布的总体；2.数据具有相同的方差；3.对于独立样本t检验，两个样本之间应相互独立；4.对于相关样本t检验，两个样本之间应具有相关性。

总结起来，两样本t检验是一种比较两个样本均值是否有显著差异的统计方法，通过计算t值和P值来进行假设检验。

根据计算得到的P值是否小于设定的显著性水平，判断两个样本的均值是否存在显著差异。

独立样本t检验原理
独立样本t检验是用于比较两个独立样本平均值差异是否显著
的统计方法。

根据中心极限定理，当样本容量大于30时，样
本平均值的抽样分布近似为正态分布。

独立样本t检验的原理
是基于此，计算两个样本平均值的差别和标准误差，进而得到
t值，并与t分布的临界值比较，判断两个样本平均值是否有
显著差异。

具体步骤如下：
1. 提出假设：设两个样本均值分别为μ1和μ2，零假设为H0：μ1=μ2，备择假设为Ha：μ1≠μ2。

2. 计算样本平均值差异：分别计算两个样本的平均值和标准差，计算两个样本平均值的差异。

3. 计算标准误差：通过两个样本的方差和样本大小计算标准误差。

4. 计算t值：用两个样本平均值的差异除以标准误差，得到t 值。

5. 比较t值：根据自由度和显著性水平查表得到t分布的临界值，将计算出的t值与临界值进行比较，如果t值小于临界值，则不能拒绝零假设，否则拒绝零假设，接受备择假设，认为两个样本的平均值存在显著差异。

第六章 假设检验基础三、两独立样本资料的t 检验概述n两独立样本的t 检验抽样：从同一对象群，随机抽取两组，各接受不同处理 或者从两个对象群，各随机抽取一组，接受相同处理 数据：两独立样本的资料目的：检验两个总体均数是否相等假定：两个总体均服从正态分布，方差相等（方差齐性）例 1 某医师要观察两种药物对原发性高血压的疗效，将诊断 为Ⅱ期高血压的 20名患者随机分为两组 （两组患者基线时血 压之间的差别没有统计学意义）;一组用卡托普利治疗，另一组用尼莫地平治疗; 3 个月后观察 舒张压下降的幅度（mm Hg）结果如下:卡托普利组（X1）：12 17 13 8 4 10 9 12 10 7尼莫地平组（X2）：11 8 12 13 9 10 8 0 7 16试比较两药平均降压效果有无差异。

经检验, 两组舒张压下降值均服从正态分布、方差齐性。

) ,( N ~ X ), , ( N ~ X 22 2 2 1 1 s m s m 1. 建立检验假设，确定检验水准H 0： 2 1 m m = , 或 0 2 1 = -m m H 1： 2 1 m m ¹ , 或 0 2 1 ¹ -m ma =0.05) n , ( N ~ X 12 1 1 sm ， ) n ,( N X 222 2 s m ~ ， )n n , ( N X X 2212 2 1 2 1 s s m m + - - ~ 检验统计量为： )11 ( 21 2 2 1 n n S X X t c+ - =2. 计算统计量2c S 是利用两样本联合估计的方差，22 2112212 (1)(1) 2cn S n S S n n -+- =+- 已知，当 H 0 成立时，统计量服从自由度 2 2 1 - + = n n n 的 t 分布。

例 1： 2) 1 ( ) 1 ( 2 1 2 22 2 1 1 2- + - + - =n n S n S n S c52. 15 210 10 27 . 4 ) 1 10 ( 58 . 3 ) 1 10 ( 22 = - + ´ - + ´ - = =+ - = ) 1 1 ( 21 2 21 n n S X X t c 454 . 0 ) 10 1 10 1 ( 52 . 15 40. 9 20 . 10 = + ´ - 3. 确定 P 值，作出推断按照a =0.05的水准，t 0.05/2,18=2.101；t=0.454< t 0.05/2,18，P >0.5，不拒绝 H 0, 差异无统计学意义；两样本所属总体方差不等怎么办？近似 t 检验（Satterthwaite近似法）例 2 为比较特殊饮食与药物治疗改善血清胆固醇 （mmol/L） 的效果，将 24名志愿者随机分成两组，每组 12人，甲组为 特殊饮食组，乙组为药物治疗组。

两独立样本T检验目的：利用来自两个总体的独立样本，推断两个总体的均值是否存在显著差异。

检验前提：样本来自的总体应服从或近似服从正态分布；两样本相互独立，样本数可以不等。

两独立样本T检验的基本步骤：提出假设原假设H_0：μ_1-μ_2=0备择假设H_1：μ_1-μ_2≠0建立检验统计量如果两样本来自的总体分别服从N(μ_1,σ_1^2 )和N(μ_2,σ_2^2 )，则两样本均值差(x_1 ) ?-x ?_2应服从均值为μ_1-μ_2、方差为σ_12^2的正态分布。

第一种情况：当两总体方差未知且相等时，采用合并的方差作为两个总体方差的估计，为：s^2=((n_1-1) s_1^2+(n_2-1) s_2^2)/(n_1+n_2-2)则两样本均值差的估计方差为：σ_12^2=s^2 (1/n_1 +1/n_2 )构建的两独立样本T检验的统计量为：t= ((x_1 ) ?-x ?_2)/√(s^2 (1/n_1 +1/n_2 ) )此时，T统计量服从自由度为n_1+n_2-2个自由度的t分布。

第二种情况：当两总体方差未知且不相等时，两样本均值差的估计方差为：σ_12^2=(s_1^2)/n_1 +(s_2^2)/n_2构建的两独立样本T检验的统计量为：t= ((x_1 ) ?-x ?_2)/√((s_1^2)/n_1 +(s_2^2)/n_2 )此时，T统计量服从修正自由度的t分布，自由度为：f= ((s_1^2)/n_1 +(s_2^2)/n_2 )^2/(((s_1^2)/n_1 )^2/n_1 +((s_2^2)/n_2 )^2/n_2 )可见，两总体方差是否相等是决定t统计量的关键。

所以在进行T检验之前，要先检验两总体方差是否相等。

SPSS中使用方差齐性检验（Levene F检验）判断两样本方差是否相等近而间接推断两总体方差是否有显著差异。

三、计算检验统计量的观测值和p值将样本数据代入，计算出t统计量的观测值和对应的概率p值。

操作方法
01
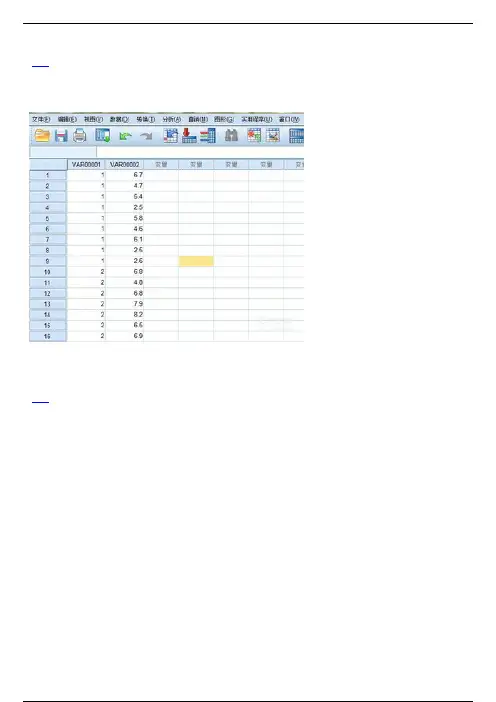
首先需要输入数据，t检验数据的输入格式为区别为一列，数值为一列。

02
接下是做正态性检验。

首先需要拆分文件，对两组数据分别做检验。

即数据——拆分文件
03
然后点一下比较组，把组别调入分组方式这里，再点击确定。

这样就拆分完毕了。

04
继续点分析——非参数检验——旧对话框——1-样本K-S
05
这样就弹出了正态性检验的对话框，将需要分析的数值调入右边的框框，然后勾选上下方检验分布的第一个，正态（也写为常规，一般默认已经勾上），然后点击确定（数值调入右边后，确定键变为可用）
06
查看结果，第一组的正态性检验P=0.798，第二组为P=0.835，可认为近似正态分布。

07
接着取消拆分。

数据——拆分文件，在跳出来的框框中点一下第一个（分组所有组），然后点确定
08
然后点分析——比较均值——独立样本t检验
09
将组别调入分组变量，数值调入检验变量
10
接着点一下分组变量下方的定义组，在弹出来的框框中输入组别1、2，再点继续——确定
11
结果出来了。

第一个表格是两组数据的例数、均值、标准差和均数的标准误。

第二个表格前部是方差齐性检验，可看到P=0.141＞0.05，具有方差齐性，
然后t检验的P值为0.007，可认为差异有统计学意义。

独立样本t检验的前提条件
独立样本t检验是一种用于比较两组独立样本均值差异的统计
方法。

在进行独立样本t检验之前，需要满足以下前提条件：
1. 样本来自于正态分布总体。

2. 两组样本方差相等，或两组样本方差差异不大。

3. 两组样本之间独立，即两组样本中的观测值之间没有相关性。

如果以上前提条件不满足，则可能会导致检验结果的误差和失真。

在进行独立样本t检验之前，应该对数据进行正态性检验和方差齐性检验，以确保数据符合前提条件。

如果数据不符合前提条件，则可以考虑其他的非参数检验方法。

- 1 -。

两独立样本t检验在统计学的领域中，两独立样本 t 检验是一种常用且重要的分析方法。

它帮助我们比较两个独立组之间的均值差异，从而得出有价值的结论。

想象一下这样的场景，我们想知道男性和女性在某项能力测试中的平均得分是否有差异，或者不同地区的学生在某学科的平均成绩是否不同。

这时候，两独立样本 t 检验就派上用场了。

两独立样本 t 检验的基本前提是，这两个样本是相互独立的，也就是说一个样本中的观察值不会影响另一个样本中的观察值。

而且，样本数据应该来自于正态分布的总体。

为了更好地理解这个检验，我们先来看看它的数学原理。

两独立样本 t 检验的核心是计算 t 值。

t 值的计算公式看起来可能有点复杂，但其实背后的逻辑并不难。

它主要是比较两个样本均值的差异与两个样本的标准差和样本量之间的关系。

假设我们有两个样本，分别为样本 A 和样本 B。

样本 A 的均值为｀X₁` ，标准差为｀S₁` ，样本量为｀n₁` ；样本 B 的均值为｀X₂` ，标准差为｀S₂` ，样本量为｀n₂` 。

那么 t 值的计算公式就是：＼t ＝＼frac{X₁X₂}｛＼sqrt{＼frac{S₁²}｛n₁} ＋＼frac{S₂²}｛n₂}｝｝＼计算出 t 值后，我们就可以根据自由度（通常为｀n₁＋ n₂ 2` ）和给定的显著性水平（比如常见的 005），在 t 分布表中查找对应的临界值。

如果计算得到的 t 值大于临界值，我们就可以拒绝原假设，认为两个样本的均值存在显著差异；反之，如果 t 值小于临界值，我们就不能拒绝原假设，认为两个样本的均值没有显著差异。

接下来，我们通过一个实际的例子来看看两独立样本 t 检验是如何应用的。

假设我们想研究一种新的教学方法对学生数学成绩的影响。

我们随机选取了两个班级，一个班级采用传统教学方法（称为A 班），另一个班级采用新的教学方法（称为 B 班）。

在学期结束后，我们对两个班级的学生进行了数学考试，并记录了他们的成绩。

在SPSS中利用均数和标准差做两独立样本t检验在SPSS中利用均数和标准差做两独立样本t检验统计学中的t检验是一种经典的假设检验方法，广泛应用于研究中两个独立样本的均值是否存在显著差异。

而SPSS （Statistical Package for the Social Sciences）是一款能够进行统计数据分析的专业软件，它提供了方便快捷进行t检验的功能。

本文将详细介绍在SPSS中如何通过均数和标准差进行两独立样本t检验。

首先，我们需要准备两组独立的样本数据。

假设我们正在研究两种不同疗法对患者疼痛程度的影响，我们随机选择了100名患者，将他们分为两组，分别接受疗法A和疗法B，然后记录他们的疼痛程度数据。

接下来，我们打开SPSS软件，并导入我们准备好的数据。

在菜单栏中选择“文件（File）”，然后选择“导入（Import）”，再选择“数据（Data）”。

然后我们选择我们的数据文件，并点击“打开（Open）”按钮，我们的数据将会被导入到SPSS中。

在导入数据后，我们需要检查数据的质量和健康程度。

我们可以使用SPSS的描述性统计功能，来获取样本的均值和标准差。

首先，选择菜单栏中的“分析（Analyse）”，然后选择“描述统计（Descriptive Statistics）”，再选择“统计（Statistics）”。

在弹出的对话框中勾选“平均值（Mean）”和“标准差（Standard Deviation）”，然后点击“确定（OK）”按钮。

SPSS将会生成两组样本的均值和标准差信息。

在获得两组样本的均值和标准差之后，我们可以进行两独立样本t检验来检验两组样本均值是否存在显著差异。

可以使用SPSS的独立样本t检验功能来进行分析。

选择菜单栏中的“分析（Analyse）”，然后选择“比较手段（Compare Means）”，再选择“独立样本t检验（Independent-Samples T Test）”。

在弹出的对话框中，选择我们的两组样本数据，点击“变量（Variables）”按钮，将我们的自变量和因变量添加到列表中。

两独立样本T检验SPSS操作详解以下是步骤详解：1.打开SPSS软件，并导入数据文件。

在“文件”菜单中选择“打开”选项，浏览并选择你的数据文件，并点击“打开”。

数据文件需要包含两组要比较的两个变量。

2.选择菜单中的“分析”选项，然后选择“比较均值”子选项，再选择“独立样本T检验”。

3.在弹出的独立样本T检验对话框中，将你要比较的两个变量移动到变量框中。

其中一个变量移动到“依赖变量”框中，另一个变量移动到“提取组变量”框中。

4.点击“定义组”按钮，在出现的对话框中输入两个组的编号，并点击“添加”按钮。

然后关闭“定义组”对话框。

5.在独立样本T检验对话框中，确定其他参数，如显著性水平（默认为0.05）和描述统计量选项。

6.点击“确定”按钮运行分析。

SPSS将计算出两组的均值、标准差、样本大小等统计量，并给出T值、自由度和显著性水平。

7.分析结果将显示在输出窗口的“独立样本T检验”表中。

主要关注的结果包括均值差异、T值、自由度和显著性水平。

8.可以根据需要导出分析结果。

在输出窗口中选择你感兴趣的表格或图表，然后在菜单中选择“文件”选项，再选择“另存为”选项，将分析结果保存为你想要的格式。

需要注意的是，在进行两独立样本T检验之前，要确保数据满足T检验的假设：两组样本是独立的、来自正态分布总体和方差齐性。

如不满足这些假设，可以考虑使用非参数检验或进行数据转换。

此外，对于SPSS软件的具体操作细节可能会因软件版本而有些差异，但基本的步骤和参数设置是相同的。

以上就是两独立样本T检验SPSS操作的详解。

通过SPSS软件进行数据分析可以更方便地得到结果，并为研究者提供科学依据。

独立样本t检验的前提条件
独立样本t检验是一种常用的统计方法，主要用于比较两组独立样本的均值是否有显著差异。

在进行独立样本t检验时，需要满足以下前提条件：
1.样本独立性。

即两组样本之间相互独立，互不影响。

如果两组样本之间存在相关性，就不能使用独立样本t检验。

2.正态分布性。

两组样本的数据应该服从正态分布。

可以通过直方图或正态概率图来检验数据是否符合正态分布。

3.方差齐性。

两组样本的方差应该相等，即方差齐性。

可以使用Levene检验或Bartlett检验来检验方差是否齐性。

如果以上前提条件没有得到满足，就不能使用独立样本t检验。

在这种情况下，可以考虑使用非参数检验方法，如Mann-Whitney U检验等。

- 1 -。

两独立样本T检验-SPSS步骤详解
1）首先确认是否为相互独立，没有任何关系的两组数据（如何确认）。

2）确定样本量：
（1）样本量N≥30，默认为大样本（有的要求为N≥50）进行方差齐性分析，方差齐采用两独立样本T检验，方差不齐采用秩和检验。

（2）如样本量N<30，为小样本，首先应进行各组资料正态性分布分析，如为正态分布，进行方差分析，方差齐，进行独立样本T检验，方差不齐，采用秩和检验；
如为非正态分布，采用秩和检验。

3）如确定应采用两独立样本T检验，则按照以下步骤进行分析，以两组患者收缩压水平为例，首先在SPSS“变量视图”（variable view）中对变量进行命名，可修改变量类型，定义变量宽度（即数字长度）等
随后调整到“数据视图（data view）”，录入数据
随后在上方菜单栏“分析（Analyze）”找到“比较均值（Compare Means）”，找到“独立
样本T检验（Independent Sample T Test）”，得到以下对话框：
将变量收缩压选入“检验变量”，分组情况选入“分组变量”，点击“定义组”，得到以下对话框：
定义组1为“1”，定义组2为“2”，点击继续，并点击“独立样本T检验”对话框（即上一对话框）中的“确定”，得到以下数据：
1组均值±标准差为126.25±12.45，2组均值±标准差为168.75±16.25
一般不确定数据方向，应检测双尾P值（Sig-two tail）=0.000，P<0.05,组间差异有统计学意义。

当确定2组数据一定大于1组时（即数据方向一定），可选用单尾P值，否则选用双尾P值。

两独立样本t检验与两配对样本t检验的异同在统计学中，t检验是一种用于比较两个样本均值是否有显著差异的常用方法。

在实际应用中，我们通常会遇到两种常见的t检验方法，即两独立样本t检验和两配对样本t检验。

本文将详细介绍这两种方法的异同点。

一、两独立样本t检验两独立样本t检验用于比较两个独立样本的均值是否有差异。

通常情况下，我们希望了解两个样本是否来自于同一总体分布。

1. 假设检验：- 零假设（H0）：两个样本的均值相等。

- 备择假设（H1）：两个样本的均值不相等。

2. 检验统计量：两独立样本t检验的检验统计量为：t = (x1 - x2) / sqrt(S1^2 / n1 + S2^2 / n2)其中，x1和x2分别为两个样本的均值，S1和S2分别为两个样本的标准差，n1和n2分别为两个样本的观测值个数。

3. 确定拒绝域：根据显著性水平（α）和自由度（df）来确定拒绝域。

在两独立样本t检验中，自由度为 df = n1 + n2 - 2。

根据给定的显著性水平和自由度，我们可以在t分布表中找到对应的临界值。

4. 检验决策：如果计算得到的检验统计量t的绝对值大于临界值，我们就可以拒绝零假设。

否则，我们接受零假设，认为两个样本的均值相等。

二、两配对样本t检验两配对样本t检验用于比较相对于同一组观测对象（配对样本）的两个相关变量之间的均值差异。

它适用于进行前后观测、对照实验等研究。

1. 假设检验：- 零假设（H0）：配对样本的均值差等于0。

- 备择假设（H1）：配对样本的均值差不等于0。

2. 检验统计量：两配对样本t检验的检验统计量为：t = (x d - μd) / (sd / sqrt(n))其中，x d为配对样本均值差的平均值，μd为期望的均值差（通常为0），sd为样本均值差的标准差，n为样本容量。

3. 确定拒绝域：与两独立样本t检验相似，根据显著性水平和自由度来确定拒绝域。

在两配对样本t检验中，自由度为 df = n - 1。