下载文档原格式
例题
比较两批电子器材的电阻，随机抽取的样本测量电阻如题表2所示，试比较两批电子器材的电阻是否相同？（提示：需考虑方差齐性问题）
分析步骤：
单击工具栏“分析”——>单击“比较均值”——>单击“单因素ANOVA检验”——>因变量列表置为电阻——>因子置为类别——>选项——>选中方差齐性检验
图1 单因素ANOVA检验
图2 统计
单击工具栏“分析”——>单击“比较均值”——>单击“独立样本T检验”——>检验变量置为电阻——>单击定义组——>填入A批、B批——>单击“确定”
图3 独立样本T检验结果展示：
表4：独立样本检验
结果分析：
假设A,B两批电阻相互独立且均服从正态分布。
H0：u1-u2＝0，两批电阻器材的电阻相同
H1：u1-u2≠0，两批电阻器材的电阻不相同
1、查看表4莱文方差等同性检验（levene），假定等方差（显著性为0.435>0.05，代表方差是齐性的），我们看第一行数据。
t检验结果显示，t=1.648，v=12，P=0.125>0.05，按照检验水准，接受H0，拒绝H1，故两批电阻器材的电阻相同。
2、查看表4莱文方差等同性检验（levene），不假定等方差，我们看第二行数据。
t’检验结果显示，t=1.648，v=10.671，P=0.129>0.05，按照检验水准，接受H0，拒绝H1，故两批电阻器材的电阻相同。
在统计学中，我们往往从样本的特性推知随机变量总体的特性。
但由于总体中个体之间存在差异，样本的统计量和总体的参数之间往往会有误差。
因此，均值不相等的样本未必来自不同分布的总体，而均值相等的样本未必来自有相同分布的总体。
也就是说，如何从样本均值的差异推知总体的差异，这就是均值比较的内容。
SPSS提供了均值比较过程，在主菜单栏单击“Analyze”菜单下的“Compare Means”项，该项下有5个过程，如图4-1。
平均数比较Means过程用于统计分组变量的的基本统计量。
这些基本统计量包括：均值（Mean）、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。
Means过程还可以列出方差表和线性检验结果。
[例子]调查了棉铃虫百株卵量在暴雨前后的数量变化，统计暴雨前和暴雨后的统计量，其数据如下：暴雨前 110 115 133 133 128 108 110 110 140 104 160 120 120暴雨后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”文件中。
1）准备分析数据在数据编辑窗口输入分析的数据，如图4-2所示。
或者打开需要分析的数据文件“DATA4-1.SAV”。
图4-2 数据窗口2）启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。
出现对话框如图4-3。
图4-3 Means设置窗口3）设置分析变量从左边的变量列表中选中“百株卵量”变量后，点击变量选择右拉按钮，该变量就进入到因子变量列表“Dependent List:”框里，用户可以从左边变量列表里选择一个或多个变量进行统计。
从左边的变量列表中选中“调查时候”变量，点击“Independent List”框左边的右拉按钮，该变量就进入分组变量“IndependentList”框里，用户可以从左边变量列表里选择一个或多个分组变量。
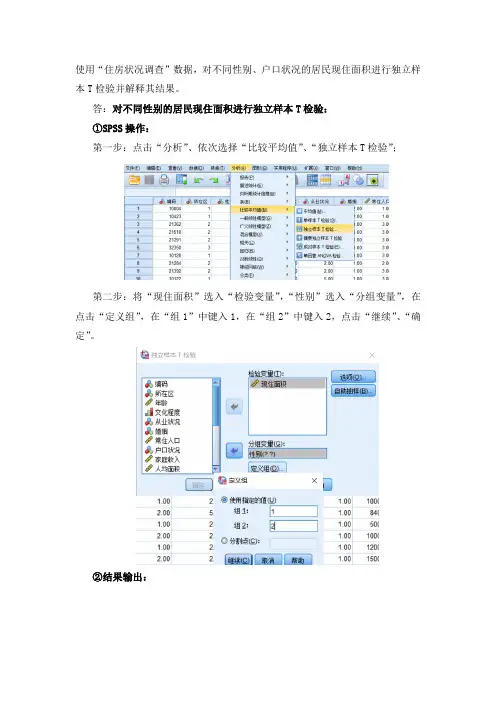
使用“住房状况调查”数据，对不同性别、户口状况的居民现住面积进行独立样本T检验并解释其结果。
答：对不同性别的居民现住面积进行独立样本T检验：①SPSS操作：第一步：点击“分析”、依次选择“比较平均值”、“独立样本T检验”；第二步：将“现住面积”选入“检验变量”，“性别”选入“分组变量”，在点击“定义组”，在“组1”中键入1，在“组2”中键入2，点击“继续”、“确定”。
②结果输出：③结果解读：先用F检验对不同性别的居民现住面积的方差是否向相等加以验证，然后利用t检验对不同性别的居民现住面积的均值是否存在差异进行检验。
从独立样本检验输出图中可以看到：F统计量为1.598，p值为0.206，在显著性水平0.05下，p值大于0.05，不拒绝原假设，即认为不同性别的居民现住面积的方差相等，没有差别。
由于不同性别的居民现住面积的方差没有差别，t检验将看假定等方差一栏。
t统计量为2.982，p值为0.003，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同性别的居民现住面积的均值有显著性差异。
对不同户口状况的居民现住面积进行独立样本T检验：④SPSS操作：第一步：点击“分析”、依次选择“比较平均值”、“独立样本T检验”；第二步：将“现住面积”选入“检验变量”，“户口状况”选入“分组变量”，在点击“定义组”，在“组1”中键入1，在“组2”中键入2，点击“继续”、“确定”。
⑤结果输出：⑥结果解读：先用F检验对不同户口状况的居民现住面积的方差是否向相等加以验证，然后利用t检验对不同户口状况的居民现住面积的均值是否存在差异进行检验。
从独立样本检验输出图中可以看到：F统计量为5.966，p值为0.015，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同户口状况的居民现住面积的方差存在显著差异。
由于不同户口状况的居民现住面积的方差存在显著差异，t检验将看不假定等方差一栏。
t统计量为3.314，p值为0.001，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同户口状况的居民现住面积的均值有显著性差异。
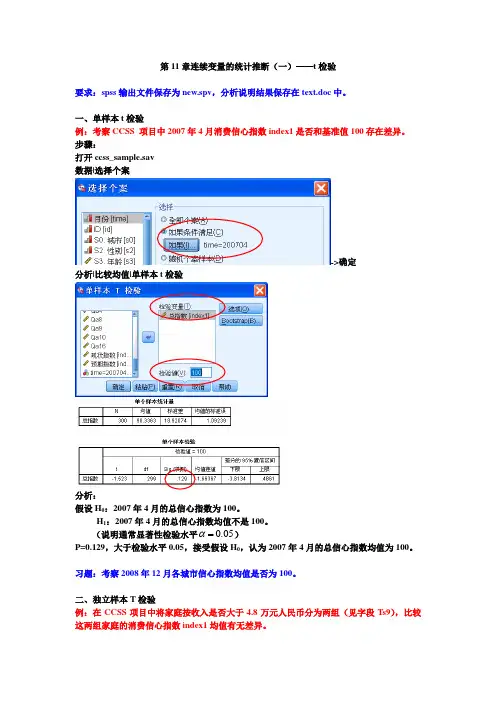
第11章连续变量的统计推断（一）——t 检验要求：spss 输出文件保存为new.spv ，分析说明结果保存在text.doc 中。
一、单样本t 检验例：考察CCSS 项目中2007年4月消费信心指数index1是否和基准值100存在差异。
步骤：打开ccss_sample.sav 数据|选择个案->确定分析|比较均值|单样本t 检验分析：假设H 0：2007年4月的总信心指数为100。
H 1：2007年4月的总信心指数均值不是100。
（说明通常显著性检验水平05.0=α）P=0.129，大于检验水平0.05，接受假设H 0，认为2007年4月的总信心指数均值为100。
习题：考察2008年12月各城市信心指数均值是否为100。
二、独立样本T 检验例：在CCSS 项目中将家庭按收入是否大于4.8万元人民币分为两组（见字段Ts9），比较这两组家庭的消费信心指数index1均值有无差异。
步骤：说明：由于上题选择部分记录，而本题对所有记录分析，所以先要选择全部记录。
数据|选择个案|全部个案|确定分析|均值检验|独立样本T检验分析：Levene方差齐性检验，p=0.027，小于0.05，认为两个样本所在总体的方差不齐。
假设H0：两个家庭收入级别在总指数上没有差异。
H1：两个家庭收入级别在总指数上有差别。
选用假设方差不相等的t检验结果，p=0.000，小于0.05，拒绝H0，认为两个家庭收入级别在总指数上有差异。
习题：在CCSS项目中，以2007年4月的数据为例，分析不同家庭收入等级（Ts9）的信心指数index1均值有无差异。
三、配对设计样本均数的比较例：用某药治疗10名高血压病人，对每一个病人治疗前后的舒张压（mmHg）进行了测试，问该药有无降压作用。
数据ptest1.sav步骤：2、配对t检验分析|均值比较|配对样本T检验分析：假设H0：同一病人治疗前后的舒张压没有差异。
H1：同一病人治疗前后的舒张压有差异。
一、问题与数据某班级老师拟比较该班级本次考试中，男生和女生的考试成绩是否有差异，该班级男生和女生各有20名同学，变量名记录为gender，分别赋值为1和2，考试成绩变量名记录为score，部分数据如图1。
图1 部分数据二、对问题分析研究者拟分析两组数据均值是否有差异，即判断男生和女生的成绩是否有差异。
针对这种情况，我们可以使用独立样本t检验，但需要先满足6项假设：假设1：观测变量为连续变量，如本研究中的成绩为连续变量。
假设2：观测变量可分为2组，如本研究中分为男生和女生。
假设3：观测值之间相互独立，如本研究中各位研究对象的信息都是独立的，不存在相互干扰。
假设4：观测变量不存在显著的异常值。
假设5：观测变量在各组内接近正态分布。
假设6：两组的观测变量的方差相等。
假设1-3取决于研究设计和数据类型，本研究数据符合假设1-3。
那么应该如何检验假设4-6，并进行独立样本t检验呢？三、SPSS操作假设4和假设5可通过以下方式检验。
假设6的检验结果可在结果解释部分查看。
3.1 检验假设4：观测变量不存在显著的异常值在主界面点击Analyze→Descriptive Statistics→Explore，弹出Explore对话框，如图2。
在对话框中将score变量放入Dependent List栏，并将gender变量放入 Factor List栏。
图2 Explore点击Plots，取消对Descriptive栏内 Stem-and-leaf选项的选择，并点击Normality plots with tests选项，点击Continue→OK。
如图3。
图3 Explore: Plots 经上述操作，SPSS输出箱式图。
如图4。
图4 箱式图SPSS中，数据点与箱子边缘的距离大于1.5倍箱身长度，则定义为异常值，以圆点（°）表示；与箱子边缘的距离大于3倍箱身长度，则定义为极端值，以星号（*）表示。
圆点或星号附近的数值是SPSS系统的自动编码（Data View窗口中最左侧蓝色一列中的编码）。
SPSS-比较均值-独立样本T检验案例解析2011-08-26 14:55在使用SPSS进行单样本T检验时，很多人都会问，如果数据不符合正太分布，那还能够进行T检验吗？而大样本，我们一般会认为它是符合正太分布的，在鈡型图看来，正太分布，基本左右是对称的，一般具备两个参数，数学期望和标准方差，即：N(p, Q)如果你的样本数非常少，一般需要进行正太分布检验，检验的方法网上很多，我就不说了下面以“雄性老鼠和雌性老鼠分别注射了某种毒素，经过观察分析，进行随机取样，查看最终老鼠是否活着。
问题：很多人认为，雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多？我们将通过进行统计分析来认证这个假设是否成立。
下面进行参数设置：a 代表：雄性老鼠b代表：雌性老鼠tim 代表：生存时间，即指经过多长时间后，去查看结果0 代表：结果死亡1 代表：结果活着随机抽取的样本，如下所示：打开SPSS- 分析---检验均值---独立样本T检验，如下图所示：将你要分析的变量，移入右边的框内，再将你要进行分组的变量移入“分组变量”框内，“组别group（）里面的两个参数，不能够随意设置，必须要跟样本里面的数字一致点击确定后，分析结果，如下所示：从组统计量可以看出，雄性老鼠的存活下来的均值为0.73，但是雌性老鼠存活下来的均值为1.00，很明显，雌性老是存活下来的个数明显比雄性老鼠多，但是一般我们不看这个结果，为什么？因为样本不够大，如果将样本升至10000个？也许这个均值将会发生变化，不具备统计学意义，我们一般只看独立样本检验的结果。
独立样本检验，提供了两种方法：levene检验和均值T检验两种方法Levene检验主要用来检验原假设条件是否成立，（即：假设方差相等和方差不相等两种情况）如果SIG>0.05，证明假设成立，不能够拒绝原假设，如果SIG<0.05，证明假设不成立，拒绝原假设。
进行levene检验结果判断是第一步，从上图，可以看出 sig<0.05 方差相等的假设不成立，所以看第二行，方差不相等的情况sig=0.082>0.05 即说明 P 值大于显著性水平，不应该拒绝原假设：即指：雌性老鼠和雄性老鼠在注射毒液后，存活下来的个数没有显著的差异本次分析的结果，不支持，很多人认为的：雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多的结论。
SPSS-比较均值-独立样本T检验案例解析
2011-08-26 14:55
在使用SPSS进行单样本T检验时，很多人都会问，如果数据不符合正太分布，那还能够进行T检验吗？而大样本，我们一般会认为它是符合正太分布的，在鈡型图看来，正太分布，基本左右是对称的，一般具备两个参数，数学期望和标准方差，即：N(p, Q)
如果你的样本数非常少，一般需要进行正太分布检验，检验的方法网上很多，我就不说了
下面以“雄性老鼠和雌性老鼠分别注射了某种毒素，经过观察分析，进行随机取样，查看最终老鼠是否活着。
问题：很多人认为，雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多？
我们将通过进行统计分析来认证这个假设是否成立。
下面进行参数设置：a 代表：雄性老鼠
b代表：雌性老鼠
tim 代表：生存时间，即指经过多长时间后，去查看结果
0 代表：结果死亡
1 代表：结果活着
随机抽取的样本，如下所示：
打开SPSS- 分析---检验均值---独立样本T检验，如下图所示：
将你要分析的变量，移入右边的框内，再将你要进行分组的变量移入“分组变量”框内，“组别group（）里面的两个参数，不能够随意设置，必须要跟样本里面的数字一致
点击确定后，分析结果，如下所示：
从组统计量可以看出，雄性老鼠的存活下来的均值为0.73，但是雌性老鼠存活下来的均值为1.00，很明显，雌性老是存活下来的个数明显比雄性老鼠多，但是一般我们不看这个结果，为什么？因为样本不够大，如果将样本升至10000个？也许这个均值将会发生变化，不具备统计学意义，
我们一般只看独立样本检验的结果。
独立样本检验，提供了两种方法：levene检验和均值T检验两种方法
Levene检验主要用来检验原假设条件是否成立，（即：假设方差相等和方差不相等两种情况）如果SIG>0.05，证明假设成立，不能够拒绝原假设，如果
SIG<0.05，证明假设不成立，拒绝原假设。
进行levene检验结果判断是第一步，从上图，可以看出 sig<0.05 方差相等的假设不成立，所以看第二行，方差不相等的情况
sig=0.082>0.05 即说明 P 值大于显著性水平，不应该拒绝原假设：即指：雌性老鼠和雄性老鼠在注射毒液后，存活下来的个数没有显著的差异
本次分析的结果，不支持，很多人认为的：雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多的结论。
其实方差不相等，并不代表不符合正太分布，也不能够说有显著的差异，方差不相同，说明曲线的偏离程度不同而已。
