下载文档原格式
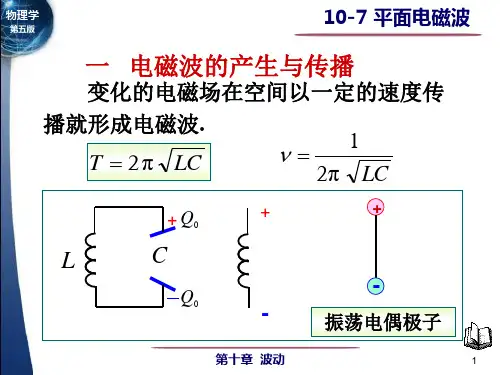
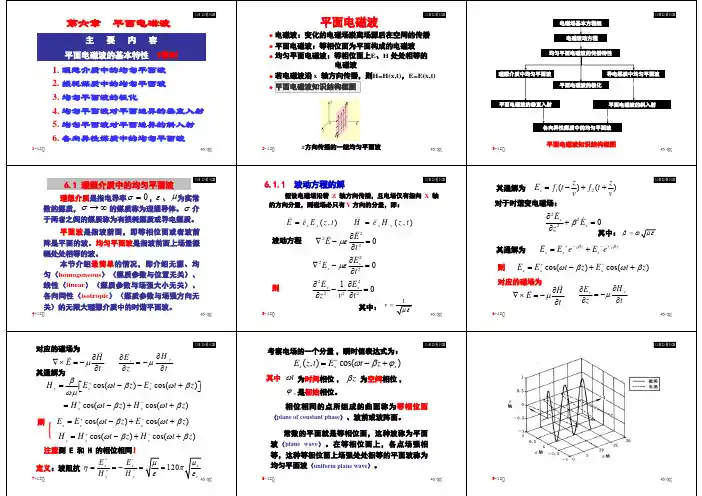
第六章主平面电磁波要 内 容 9学时平面电磁波电磁波：变化的电磁场脱离场源后在空间的传播 平面电磁波：等相位面为平面构成的电磁波 均匀平面电磁波：等相位面上E、H 处处相等的 电磁波 若电磁波沿 x 轴方向传播，则H=H(x,t)，E=E(x,t) 平面电磁波知识结构框图电磁场基本方程组 电磁波动方程 均匀平面电磁波的传播特性平面电磁波的基本特性1. 理想介质中的均匀平面波 2. 损耗媒质中的均匀平面波 3. 均匀平面波的极化 4. 均匀平面波对平面边界的垂直入射 5. 均匀平面波对平面边界的斜入射 6. 各向异性媒质中的均匀平面波1-120 2-120理想介质中均匀平面波 平面电磁波的极化导电媒质中均匀平面波平面电磁波的垂直入射平面电磁波的斜入射各向异性媒质中的均匀平面波x方向传播的一组均匀平面波3-120平面电磁波知识结构框图数的媒质， σ → ∞ 的媒质称为理想导体。
σ 介 于两者之间的媒质称为有损耗媒质或导电媒质。
6.1 理想介质中的均匀平面波 理想介质是指电导率 σ = 0 ，ε 、 μ 为实常6.1.1波动方程的解其通解为假设电磁场沿着 Z 轴方向传播，且电场仅有指向 X 轴 的方向分量，则磁场必只有 Y 方向的分量，即：z z E x = f1 (t − ) + f 2 (t + ) v v ∂ 2 Ex + β 2 Ex = 0 ∂z 2对于时谐变电磁场：E = ex E x ( z, t )波动方程H = ey H y (z,t)其通解为 则平面波是指波前面，即等相位面或者波前 阵是平面的波。
均匀平面波是指波前面上场量振 幅处处相等的波。
本节介绍最简单的情况，即介绍无源、均 匀（homogeneous）（媒质参数与位置无关）、 线性（linear）（媒质参数与场强大小无关）、 各向同性（isotropic）（媒质参数与场强方向无 关）的无限大理想介质中的时谐平面波。
4-120 5-120则∂E 2 =0 ∂t 2 ∂E 2 ∇ 2 E x − με 2x = 0 ∂t 2 ∂ E x 1 ∂E x2 − =0 ∂z 2 v 2 ∂t 2 ∇ 2 E − με其中： v =其中： β = ω μ εEx = Ex + e− jβ z + Ex − e+ jβ zE x = E x+ cos(ω t − β z ) + E x− cos(ω t + β z )对应的磁场为1∇ × E = −μ6-120με∂H ∂t∂H y ∂E x = −μ ∂z ∂t对应的磁场为∇ × E = −μ其通解为∂H ∂t∂H y ∂E x = −μ ∂z ∂t考察电场的一个分量 ，瞬时值表达式为：Ex ( z, t ) = Ex+ cos(ωt − β z + ϕx )其中Hy =β ⎡ E + cos(ω t − β z ) − E x− cos(ω t + β z ) ⎤ ⎦ ωμ ⎣ xωt 为时间相位 ， β z 为空间相位 ， ϕ x 是初始相位。
第八章 平面电磁波8-1 导出非均匀的各向同性线性媒质中，正弦电磁场应该知足的波动方程及亥姆霍兹方程。
解 非均匀的各向同性线性媒质中，正弦电磁场应该知足的麦克斯韦方程如下：⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇)(),()(0),()(),()(),(),()(),(),(r r E r r H r r H r r E r E r r J r H ρεμμεt t t t t t t t t ， 别离对上面两式的两边再取旋度，利用矢量公式A A A 2)(∇-⋅∇∇=⨯∇⨯∇，得⎪⎪⎭⎫ ⎝⎛∇⋅-∇+∂∂+∂∂⨯∇=∂∂-∇)()(),(),(),()(),()(),()()(),(222r r r E r r J r r H r r E r r r E εερμμμεt t t t t t t t t⎪⎪⎭⎫ ⎝⎛∇⋅∇-∂∂⨯∇-⨯-∇=∂∂-∇μμεμε)(),(),()(),(),()()(),(222r r H r E r r J r H r r r H t t t t t t t则相应的亥姆霍兹方程为⎪⎪⎭⎫⎝⎛∇⋅-∇++⨯∇=+∇)()()()()()(j )()(j )()()()(22r r r E r r J r r H r r E r r r E εερωμμωμεω⎪⎪⎭⎫ ⎝⎛∇⋅∇-⨯∇-⨯-∇=+∇μμεωμεω)()()()(j )()()()()(22r r H r E r r J r H r r r H8-2 设真空中0=z 平面上散布的表面电流t J s x s sin 0ωe J =，试求空间电场强度、磁场强度及能流密度。
解 0=z 平面上散布的表面电流将产生向z +和z -方向传播的两个平面波，设z > 0区域中的电场和磁场别离为)(1z,t E ，)(1z,t H ，传播方向为z +；而z < 0区域中的场强为)(2z,t E 和)(2z,t H ，传播方向为z -。
