7电磁场与电磁波-第七章(上)图片
- 格式:ppt
- 大小:2.14 MB
- 文档页数:73






第7章 导行电磁波前面我们讨论了电磁波在无界空间的传播以及电磁波对平面分界面的反射与透射现象。
在这一章中我们将讨论电磁波在有界空间的传播,即导波系统中的电磁波。
所谓导波系统是指引导电磁波沿一定方向传播的装置,被引导的电磁波称为导行波。
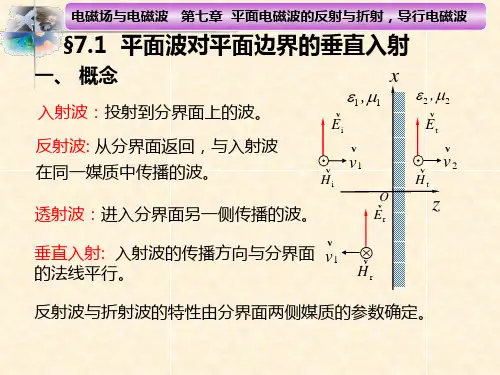
常见的导波系统有规则金属波导(如矩形波导、圆波导)、传输线(如平行双线、同轴线)和表面波波导(如微带线),图7.0.1给出了一些常见的导波系统。
导波系统中电磁波的传输问题属于电磁场边值问题,即在给定边界条件下解电磁波动方程,这时我们可以得到导波系统中的电磁场分布和电磁波的传播特性。
在这一章中,将用该方法讨论矩形波导、圆波导和同轴线中的电磁波传播问题以及谐振腔中的场分布及相关参数。
然而,当边界比较复杂时,用这种方法得到解析解就很困难,这时如果是双导体(或多导体)导波系统且传播的电磁波频率不太高,就可以引入分布参数,用“电路”中的电压和电流等效前面波导中的电场和磁场,这种方法称为“等效传输线”法。
这一章我们还将用该方法讨论平行双线和同轴线中波的传播特性。
7.1导行电磁波概论任意截面的均匀导波系统如图7.1.1所示。
为讨论简单又不失一般性,可作如下假设: (1)波导的横截面沿z 方向是均匀的,即导波内的电场和磁场分布只与坐标x ,y 有关,与坐标z 无关。
(2)构成波导壁的导体是理想导体,即σ=∞。
(3)波导内填充的媒质为理想介质,即0σ=,且各向同性。
(4)所讨论的区域内没有源分布,即0ρ=0=J 。
a 矩形波导b 圆柱形波导c 同轴线传输线d 双线传输线e 微带线图7.0.1 常见的几种导波系统(5)波导内的电磁场是时谐场,角频率为ω。
设波导中电磁波沿+z 方向传播,对于角频率为ω的时谐场,由假设条件(1)和(2)可将其电磁场量表示为()()()(),,,,,,,z z x y z x y e x y z x y e γγ--==E E H H (7.1.1)式中γ称为传播常数,表征导波系统中电磁场的传播特性。


第7章 导行电磁波1、 求内外导体直径分别为0.25cm 和 0.75cm 空气同轴线的特性阻抗; 在此同轴线内外导体之间填充聚四氟乙烯( 2.1r ε=),求其特性阻抗与300MHz 时的波长。
解:空气同轴线的特性阻抗00.7560ln60ln =65.9170.25b Z a ==Ω 聚四氟乙烯同轴线:00.75=41.404ln345.487 0.25b Z a ===Ω80.69v m f λ==== 2、在设计均匀传输线时,用聚乙烯(εr =2.25)作电介质,忽略损耗⑴ 对于300Ω的双线传输线,若导线的半径为0.6mm ,线间距应选取为多少?⑵ 对于75Ω的同轴线,若内导体的半径为0.6mm ,外导体的内半径应选取为多少? 解:⑴ 双线传输线,令d 为导线半径,D 为线间距,则0110 ln , ln1 300 ln3.75, 25.5D L C D d dDZ dDD mm dμπεππ=====∴== ⑵ 同轴线,令a 为内导体半径,b 为外导体内半径,则0112 ln , 2lnb L C b a aμπεπ==01 ln 752 ln1.875, 3.91bZ abb mm aπ===∴==3、设无耗线的特性阻抗为100Ω, 负载阻抗为5050j -Ω, 试求:终端反射系数L Γ驻波比VSWR 及距负载0.15λ处的输入阻抗in Z 。
解:005050100112505010035L L L Z Z j j j Z Z j j ---++Γ===-=-+-+-1 2.6181L L S+Γ===-Γ()()000250501000.15100210050500.15L in L j j tan Z jZ tan d Z d Z Z jZ tan d j j tan πλβλπβλλ⎛⎫-+⨯ ⎪+⎝⎭==⨯+⎛⎫+-⨯ ⎪⎝⎭43.55 +34.16j =4、一特性阻抗为50Ω、长2m 的无耗线工作于频率200MHz ,终端阻抗为4030j +Ω,求其输入阻抗in Z 。

第七章 时变电磁场重点和难点通过位移电流的引入,导出全电流定律,说明时变电场可以产生时变磁场。
详细讲解麦克斯韦方程的积分形式和微分形式,说明时变电磁场是有旋有散的,时变电场的方向与时变磁场的方向处处相互垂直,以及麦克斯韦对于人类文明和进步的伟大贡献。
讲解时变电磁场的边界条件时,应与静态场进行比较,尤其要介绍理想导电体的边界条件。
讲解位函数时,应强调罗伦兹条件的重要性。
详细讲解位函数解的物理意义,强调没有滞后效应就不可能有辐射。
指出位函数的积分解仅适用于均匀线性各向同性的媒质。
能量密度容易理解,着重讲解能流密度矢量。
时变电磁场的惟一性定理证明可以略去,但是其物理意义及其重要性必须介绍。
讲解正弦电磁场的复矢量表示方法时,应强调仅适用于频率相同的场量之间的运算。
此外,还应指出该教材使用的时间因子是e j ω t ,而不是e -i ωt 。
对于复能流密度矢量,应着重介绍其实部和虚部的物理意义,以及电场和磁场之间的相位差对于复能流密度矢量的影响。
重要公式位移电流密度:td ∂∂=DJ 全电流连续性原理:0d )( =⋅+⎰SS J J d 0)(=+⋅∇d J J全电流定律:S DJ l H d )(d ⋅∂∂+=⋅⎰⎰SlttD J H ∂∂+=⨯∇ 麦克斯韦方程:积分形式:S DJ l H d )(d ⋅∂∂+=⋅⎰⎰SltS Bl E d d ⋅∂∂-=⋅⎰⎰S l t0d =⋅⎰SS B q S=⋅⎰ d S D微分形式: t ∂∂+=⨯∇D J H t∂∂-=⨯∇B E 0=⋅∇B ρ=⋅∇D电荷守恒原理:V tSV d d ⎰⎰∂∂-=⋅ρS J t∂∂-=⋅∇ρJ 媒质特性方程: E D ε=H B μ=J E J '+= σ一般边界条件:1,0)(12=-⨯E E e n ,式中n e 为由媒质①指向媒质②的边界法向单位矢量。
对于各向同性的线性媒质,221 1εεttD D =2,0)(12=-⋅B B e n 。