电机学电子教材
- 格式:doc
- 大小:400.50 KB
- 文档页数:6

第六章同步电机 (272)6.1 概述 (272)6.1.1 同步电机的结构型式 (272)6.1.2 同步电机的励磁方式 (278)6.1.3 同步电机的冷却方式 (278)6.1.4 同步电机的额定值 (278)6.2 同步电机的运行原理 (279)6.2.1 同步发电机的空载运行 (279)6.2.2 同步电机的电枢反应 (282)6.2.3 隐极同步发电机的负载运行 (286)6.2.4 凸极同步发电机的负载运行 (291)6.3 同步发电机的运行特性 (295)6.3.1 同步发电机的运行特性 (296)6.3.2 特性曲线在参数计算中的应用 (299)6.3.3 同步发电机稳态参数的测定 (306)6.4 同步发电机的并联运行 (307)6.4.1 投入并联的条件和方法 (308)6.4.2 功率和转矩平衡方程 (311)6.4.3 功角特性 (312)6.4.4 有功功率调节与静态稳定 (314)6.4.5 无功功率调节和V形曲线 (318)6.5 同步电动机和调相机 (319)6.5.1 基本电磁关系 (319)6.5.2 无功功率调节 (322)6.5.3 起动与调速 (323)6.5.4 调相机 (326)6.6 同步发电机的不对称运行 (327)6.6.1 相序阻抗和等效电路 (327)6.6.2 不对称稳态短路 (330)6.6.3 负序和零序参数测定 (334)6.6.4 不对称运行的影响 (336)6.7 同步电机的突然短路 (337)6.7.1 超导回路磁链守恒原理 (337)6.7.2 三相突然短路过程中的基本电磁关系 (338)6.7.3 同步电机的瞬态参数 (343)6.7.4 突然短路电流及其衰减时间常数 (347)6.7.5 突然短路对电机的影响 (351)6.8 特殊用途的同步电机 (352)6.8.1 磁阻同步电动机 (352)6.8.2 磁滞同步电动机 (354)6.8.3 反应式步进电动机 (356)习题 (358)电机学第六章同步电机272第六章同步电机同步电机是交流电机的一种。


第四节交流磁路中的激磁电流和磁通、电磁感应定律?i的波形会产在交流铁心磁路中,由于铁心磁化曲线的非线性,激磁电流和主磁通m生畸变。
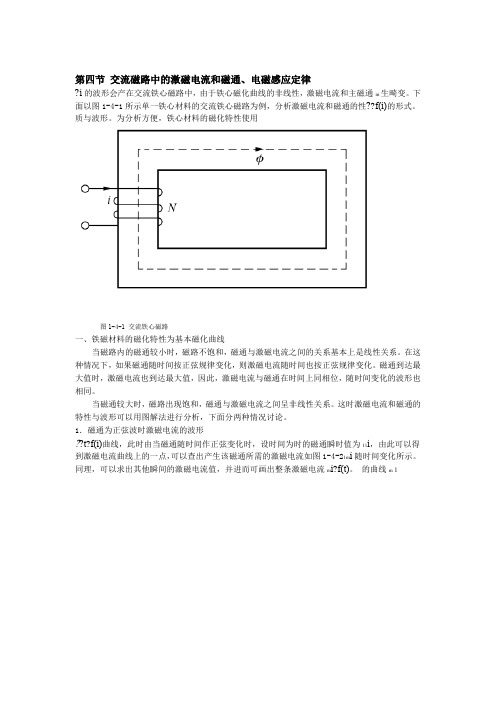
下面以图1-4-1所示单一铁心材料的交流铁心磁路为例,分析激磁电流和磁通的性??f(i)的形式。
质与波形。
为分析方便,铁心材料的磁化特性使用图1-4-1 交流铁心磁路一、铁磁材料的磁化特性为基本磁化曲线当磁路内的磁通较小时,磁路不饱和,磁通与激磁电流之间的关系基本上是线性关系。
在这种情况下,如果磁通随时间按正弦规律变化,则激磁电流随时间也按正弦规律变化。
磁通到达最大值时,激磁电流也到达最大值,因此,激磁电流与磁通在时间上同相位,随时间变化的波形也相同。
当磁通较大时,磁路出现饱和,磁通与激磁电流之间呈非线性关系。
这时激磁电流和磁通的特性与波形可以用图解法进行分析,下面分两种情况讨论。
1.磁通为正弦波时激磁电流的波形??t?f(i)曲线,此时由当磁通随时间作正弦变化时,设时间为时的磁通瞬时值为11i,由此可以得到激磁电流曲线上的一点,可以查出产生该磁通所需的激磁电流如图1-4-21m i随时间变化所示。
同理,可以求出其他瞬间的激磁电流值,并进而可画出整条激磁电流m i?f(t)。
的曲线m 11-4-2 磁通为正弦波时磁路饱和对电流波形的影响图)电流波形分解)电流波形;(b(a可以看出,当磁通随时间正弦变化且磁路饱和时,由于磁路的非线性,激1-4-2 分析图磁电流波形发生畸变,成为尖顶波。
如果将激磁电流波形进行分解,除了基波外,还包含有i的波形尖顶越严重,谐其他奇次谐波,其中以三次谐波为最大。
磁路越饱和,激磁电流m?i的相位相波也越显著。
但无论激磁电流波形尖顶有多严重,它的基波相位始终与磁通m同。
.激磁电流为正弦波时磁通的波形2?i随时间随时间作正弦变化时,利用上述的作图法,同样可以求出磁通当激磁电流m?)t?f(所示。
,如图变化的曲线1-4-3 2激磁电流为正弦波时磁路饱和对磁通波形的影响图1-4-3)磁通波形分解(b(a)磁通波形;i随时间正弦变化且磁路饱和时,磁通的波形也1-4-3可以看出,当激磁电流分析图m发生畸变,成为平顶波。

第四节 交流磁路中的激磁电流和磁通、电磁感应定律
在交流铁心磁路中,由于铁心磁化曲线的非线性,激磁电流m i 和主磁通φ的波形会产生畸变。
下面以图1-4-1所示单一铁心材料的交流铁心磁路为例,分析激磁电流和磁通的性质与波形。
为分析方便,铁心材料的磁化特性使用)(i f =φ的形式。
图1-4-1 交流铁心磁路
一、铁磁材料的磁化特性为基本磁化曲线
当磁路内的磁通较小时,磁路不饱和,磁通与激磁电流之间的关系基本上是线性关系。
在这种情况下,如果磁通随时间按正弦规律变化,则激磁电流随时间也按正弦规律变化。
磁通到达最大值时,激磁电流也到达最大值,因此,激磁电流与磁通在时间上同相位,随时间变化的波形也相同。
当磁通较大时,磁路出现饱和,磁通与激磁电流之间呈非线性关系。
这时激磁电流和磁通的特性与波形可以用图解法进行分析,下面分两种情况讨论。
1.磁通为正弦波时激磁电流的波形
当磁通随时间作正弦变化时,设时间为1t 时的磁通瞬时值为1φ,此时由)(i f =φ曲线可以查出产生该磁通所需的激磁电流1m i ,由此可以得到激磁电流曲线上的一点,如图1-4-2所示。
同理,可以求出其他瞬间的激磁电流值,并进而可画出整条激磁电流m i 随时间变化的曲线)(m t f i =。
图1-4-2 磁通为正弦波时磁路饱和对电流波形的影响
(a )电流波形;(b )电流波形分解
分析图1-4-2可以看出,当磁通随时间正弦变化且磁路饱和时,由于磁路的非线性,激磁电流波形发生畸变,成为尖顶波。
如果将激磁电流波形进行分解,除了基波外,还包含有其他奇次谐波,其中以三次谐波为最大。
磁路越饱和,激磁电流m i 的波形尖顶越严重,谐波也越显著。
但无论激磁电流m i 波形尖顶有多严重,它的基波相位始终与磁通φ的相位相同。
2.激磁电流为正弦波时磁通的波形
当激磁电流m i 随时间作正弦变化时,利用上述的作图法,同样可以求出磁通φ随时间变化的曲线)(t f =φ,如图1-4-3所示。
图1-4-3 激磁电流为正弦波时磁路饱和对磁通波形的影响
(a )磁通波形;(b )磁通波形分解
分析图1-4-3可以看出,当激磁电流m i 随时间正弦变化且磁路饱和时,磁通的波形也发生畸变,成为平顶波。
如果将磁通波形进行分解,除了基波外,亦包含有其他奇次谐波,其中也以三次谐波为最大。
磁路越饱和,磁通φ的波形平顶越严重,谐波也越显著。
但无论波形平顶有多严重,它的基波相位始终与激磁电流m i 的相位相同。
综上分析可知:激磁电流和磁通的波形是否畸变,决定于磁路是否饱和。
磁路不饱和时,磁化曲线基本上是线性的,两者的波形非常接近。
磁路饱和后,磁化曲线呈非线性,磁通与激磁电流的波形不同。
磁通为正弦波时激磁电流畸变成尖顶波;激磁电流为正弦波时磁通畸变成平顶波。
但无论是尖顶波还是平顶波,如果将其进行分解,主要成分都是基波和三次谐波。
磁通基波和激磁电流基波的相位始终相同,与磁路是否饱和以及饱和程度无关。
二、铁磁材料的磁化特性为磁滞回线
考虑磁滞现象时,铁磁材料的磁化特性为磁滞回线。
当磁通为正弦波时,通过磁滞回线,利用图解法求取激磁电流i m =f (t )的曲线,如图1-4-4所示。
可以看出,当磁通φ为正弦波时,激磁电流m i 为非正弦波。
把m i 分解成两个分量,即Fe μm i i i +=。
其中μi 分量为和φ同相位的尖顶波,与忽略磁滞现象、只考虑饱和时图1-4-2中的尖顶波完全一致;或者说,μi 是不考虑磁路有磁滞现象时的激磁电流,与基本磁化曲线相对应,称为磁化电流。
另一分量Fe i 波形近似为正弦波,相位超前于磁通φ90°、幅值为I c (与H c 相对应)。
Fe i 是反映磁滞损耗和涡流损耗的有功电流,e h Fe i i i +=,h i 是由于考虑了磁滞现象才存在的,称为磁滞损耗电流,不计磁滞现象,h i 为零。
交流磁路中除了磁滞损耗外,同时还有涡流损耗。
e i 称为涡流损耗电流。
由于h i 和e i 都反映了磁路中的铁耗,因此把它们合在一起,称为铁耗电流,
用Fe i 表示。
在各种变压器和电机中,由于铁心选用的都是较好的软磁性材料,同时又采用叠片方式,因此铁耗很小。
激磁电流中铁耗电流要比磁化电流μi 小得多。
图1-4-4 磁滞现象对激磁电流波形的影响
(a )电流波形;(b )电流波形分解
综合上述分析可知:
(1)激励产生磁通φ的电流是磁化电流μi ,它的基波与磁通φ波形同相位。
由于磁路的非线性,μi 与磁通φ的波形不一样。
当φ为正弦波时,μi 为尖顶波;当μi 为正弦波时,φ为平顶波。
(2)铁心中具有磁滞和涡流损耗。
激磁电流中除了磁化电流外,同时还存在铁心损耗电流,铁心损耗电流接近于正弦波,其相位超前于磁通90°。
(3)激磁电流是磁化电流和铁心损耗电流的合成,即m Fe i i i μ=+。
由于变压器和电机的铁心损耗很小,所以Fe i 很小,通常仅为m i 的10%左右,因此激磁电流m i 主要由μi 决定。
三、电磁感应定律
电磁感应定律描述的是磁变生电的电磁感应现象,于1831年由法拉第提出,又称法拉第电磁感应定律。
它指出,交变的磁场会产生电场,并在导体中感应电动势。
如图1-4-5所示,当规定感应电动势正方向与磁通的正方向符合右手螺旋关系时,则感应电动势与磁通对时间的变化率的负值成正比,即
t
Ψt N e d d d d -=-=φ (1-4-1) 式中:e 为回路中的感应电动势;N 为绕组匝数;φ为通过该回路面积的磁通;ψ为交链
回路的磁链,它表示N 匝线圈所匝链的总磁链,φψN =。
图1-4-5 电磁感应 根据法拉第定律可以导出,当磁场恒定,而导体在磁场中运动时,如图1-4-6(a )所示,导体中的感应电动势可表示为
⎰
⋅⨯=l B v d )(e (1-4-2) 式中:B 为磁感应强度;l 为导体的长度;v 为导体的运动速度。
感应电动势的方向可用图1-4-6(b )所示的右手定则确定。
图1-4-6 感应电动势与右手定则
(a )感应电动势;(b )右手定则
若磁场方向、导体长度方向和导体运动方向三者相互垂直时,式(1-4-2)简化为
Blv e = (1-4-3)
式(1-4--3)适用于计算恒定、均匀磁场中运动导体的切割电动势,是法拉第电磁感应定律的另一种有约束条件的表示形式, 在电机学中经常使用。
四、毕奥-萨伐尔电磁力定律
磁场最基本的特性是对场域中的载流导体有力的作用,电磁力定律是描述电与磁之间相互作用产生力的基本定律。
如图1-4-7(a )所示,取有效长度为l 的导体,导体中流过的电流为i ,导体所处的磁场为B ,则导体所受的作用力f 可表示为
⎰
⨯=B l f d i (1-4-4) 式中:l d 为导体ab 上的长度微元。
若磁场均匀且与导体相互垂直,则式(1-4-4)可简化为
Bil f = (1-4-5) 电磁力的方向可用左手定则判定,如图1-4-7(b )所示。
图1-4-7 电磁力和左手定则
(a)电磁力;(b)左手定则
五、能量守恒原理
能量守恒原理是物理学中的基本原理。
该原理可表述为:在质量不变的物理系统内,能量是守恒的,即能量不会凭空产生,亦不会凭空消灭,仅能变换其存在形式。
在电机中,能量转换包括四种能量形式,即电能、机械能、磁场储能和热能。
根据能量守恒原理,对于电动机,其能量关系为
电源输入的电能=磁场储能的增量+转换为热能的能量损耗+机械能输出
对于发电机,其能量关系为
机械能输入=磁场储能的增量+转换为热能的能量损耗+电能输出
转换为热能的能量主要包括三部分:导体中的电流在电阻中引起的电气损耗(亦称铜耗);消耗于轴承摩擦及通风中的机械损耗;电机内的磁场在铁心中产生的磁滞损耗和涡流损耗。
这些能量均转换为热能,并且是一种不可逆的过程,也就是说这部分能量很难或根本不可能再转换为电能或机械能。