第20次课 尺寸链计算的基本公式
- 格式:doc
- 大小:81.00 KB
- 文档页数:4

公差尺寸链计算公式
1.基准尺寸的确定:
在公差尺寸链的计算中,首先需要确定一个基准尺寸,作为其他尺寸的参考。
一般选择与工艺要求相符的零件尺寸作为基准尺寸。
2.公差分配:
公差分配是指根据装配要求和功能要求,按照一定比例将总公差分配到各个零件尺寸上。
公差分配的原则包括:
-公差应按照装配要求和功能要求进行分布,确保装配精度和功能要求的满足。
-尺寸公差应该从初始尺寸向装配间隙依次增大,以确保装配的顺利进行。
-公差应尽量少,以减少成本和缩小尺寸偏差。
在进行公差分配时,一般需要考虑以下几个因素:
-零件功能要求:根据零件在装配中的具体功能、运动和受力情况,确定其尺寸公差的分配。
-装配方式:根据零件的装配方式,如插入、相对位置等,确定其尺寸公差的分配。
-零件尺寸和材料:根据零件的尺寸和材料特性,确定其尺寸公差的分配。
3.最小公差计算:
最小公差是保证装配精度的关键要素,通常根据装配要求和功能要求
向下确定。
最小公差的计算需要考虑以下几个因素:
-装配要求:根据装配的要求和设定的公差限制,确定所需的最小公差。
-装配间隙:根据装配时需要的间隙和松动度,确定所需的最小公差。
-功能要求:根据零件在装配中的具体功能和使用要求,确定最小公差。
以上是公差尺寸链计算的基本原理和步骤。
实际应用中,还需要考虑
诸如公差合理化、商标公差等的因素,以确保设计的合理性和可靠性。
公
差尺寸链计算是一项复杂的工作,需要根据具体情况进行合理的分析和计算,以满足产品的装配和使用要求。

工艺尺寸链计算的基本公式
1.尺寸链总公差计算式
总公差=设计尺寸+最大便宜-最小公差
其中,设计尺寸是产品设计的理论尺寸,最大便宜是指允许的最大超
出设计尺寸的尺寸偏差,最小公差是指允许的最小尺寸偏差。
2.累积公差计算式
累积公差=√(Σ(公差1^2+公差2^2+公差3^2+...+公差n^2))
其中,Σ表示总和,公差1、公差2、公差3...公差n是从设计到加
工过程中每个环节的公差。
3.公差分配计算式
公差分配=(设计尺寸-加工尺寸)/加工余量
其中,设计尺寸是产品设计的理论尺寸,加工尺寸是实际加工得到的
尺寸,加工余量是指设计尺寸与加工尺寸之间的差值。
4.合并公差计算式
合并公差=√(公差1^2+公差2^2)
其中,公差1和公差2是两个相互独立的公差。
5.组合公差计算式
组合公差=(公差1^2+公差2^2+公差3^2+...+公差n^2)^0.5
其中,公差1、公差2、公差3...公差n是不同特征尺寸的尺寸公差。
除了这些基本公式外,还有一些特殊情况下的公式可供使用,如配合
公差的计算、紧配合公差的计算等。
需要注意的是,工艺尺寸链的计算是一个复杂的过程,需要考虑到产
品的设计要求、加工工艺的要求、材料的特性等多个因素。
公式只是工艺
尺寸链计算的一部分,实际使用中还需结合具体情况进行综合计算和分析。


第20次课尺⼨链计算的基本公式式中,—尺⼨链中第j个组成环的标准偏差。
如果各组成环的实际尺⼨都为正态分布,并且分布范围与公差带宽度⼀致,分布中⼼与公差带中⼼重合,见图8-8,则封闭环的实际尺⼨也服从正态分布,各环公差与标准偏差关系如下T0 = 6σ0T j= 6将以上两式代⼊(8-9)式,得(8—10) (8—10)式表明:封闭环公差等于所有组成环公差的⽅和根。
由图8-8可见,各组成环的中间偏差为其上、下偏差的平均值。
封闭环的中间偏差?0与组成环的中间偏差?j分别为0 =j =各组成环的中⼼尺⼨为极限尺⼨的平均值。
封闭环的中间尺⼨A0中为封闭环的基本尺⼨与其中间偏差之和:A0中 = A0+ ?0 (8-11) 组成环中间尺⼨A j中为组成环的基本尺⼨与中间偏差之和:A j中 = A j+ ?j(8-12)(8-4)和(8-5)式相加后取平均值可得-13) 即:封闭环中间尺⼨等于所有增环的中间尺⼨之和减去所有减环的中间尺⼨之和。
将上述公式整理得:(8-14) 即:封闭环中间偏差等于所有增环的中间偏差之和减去所有减环的中间偏差之和。
如果组成环的实际尺⼨不服从正态分布,⽽是其它分布,或者组成环分布中⼼偏离公差带中⼼,那么本节所述公式应加以修正,详见有关书籍。
⽤⼤数互换法解尺⼨链的步骤基本上与极值法相同。
但在计算封闭环和组成环的上、下偏差时,要先算出它们的中间偏差。
,B2=70 0 -0.03,B0 = 四、例题:在上节课图所⽰的齿轮轴装配图中:B1=100+0.140.02—0.20,求垫⽚轴向尺⼨B3为多少?列式计算∵ B0max = B1max - (B2min + B3min)∴ B3min = B1max - B2min – B0max=100.14-69.97-0.2= 29.97mm同理:B3max = B1min- B2max- B0min= 100- 70-0.02= 29.98 mm。



工艺尺寸链计算的基本公式来源:作者:发布时间:2007-08-03工艺尺寸链的计算方法有两种:极值法和概率法。
目前生产中多采用极值法计算,下面仅介绍极值法计算的基本公式,概率法将在装配尺寸链中介绍。
图 3-82 为尺寸链中各种尺寸和偏差的关系,表 3-18 列出了尺寸链计算中所用的符号。
1 .封闭环基本尺寸式中 n ——增环数目;m ——组成环数目。
2 .封闭环的中间偏差式中Δ0——封闭环中间偏差;——第 i 组成增环的中间偏差 ;——第 i 组成减环的中间偏差。
中间偏差是指上偏差与下偏差的平均值:3 .封闭环公差4 .封闭环极限偏差上偏差下偏差5 .封闭环极限尺寸最大极限尺寸 A 0max=A 0+ES 0 ( 3-27 )最小极限尺寸 A 0min=A 0+EI 0 ( 3-28 )6 .组成环平均公差7 .组成环极限偏差上偏差下偏差8 .组成环极限尺寸最大极限尺寸 A imax=A i+ES I ( 3-32 )最小极限尺寸 A imin=A i+EI I ( 3-33 )工序尺寸及公差的确定方法及示例工序尺寸及其公差的确定与加工余量大小,工序尺寸标注方法及定位基准的选择和变换有密切的关系。
下面阐述几种常见情况的工序尺寸及其公差的确定方法。
(一)从同一基准对同一表面多次加工时工序尺寸及公差的确定属于这种情况的有内外圆柱面和某些平面加工,计算时只需考虑各工序的余量和该种加工方法所能达到的经济精度,其计算顺序是从最后一道工序开始向前推算,计算步骤为:1 .确定各工序余量和毛坯总余量。
2 .确定各工序尺寸公差及表面粗糙度。
最终工序尺寸公差等于设计公差,表面粗糙度为设计表面粗糙度。
其它工序公差和表面粗糙度按此工序加工方法的经济精度和经济粗糙度确定。
3 .求工序基本尺寸。
从零件图的设计尺寸开始,一直往前推算到毛坯尺寸,某工序基本尺寸等于后道工序基本尺寸加上或减去后道工序余量。
4 .标注工序尺寸公差。

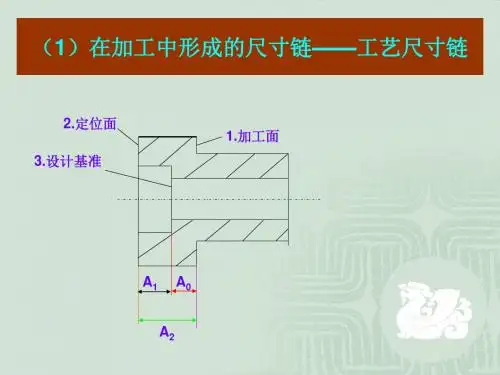
一、尺寸链及尺寸链计算公式1、尺寸链的定义在工件加工和机器装配过程中,由相互联系的尺寸,按一定顺序排列成的封闭尺寸组,称为尺寸链。
尺寸链示例2、工艺尺寸链的组成环:工艺尺寸链中的每一个尺寸称为尺寸链的环。
工艺尺寸链由一系列的环组成。
环又分为:(1)封闭环(终结环):在加工过程中间接获得的尺寸,称为封闭环。
在图b所示尺寸链中,A0是间接得到的尺寸,它就是图b所示尺寸链的封闭环。
(2)组成环:在加工过程中直接获得的尺寸,称为组成环。
尺寸链中A1与A2都是通过加工直接得到的尺寸,A1、A2都是尺寸链的组成环。
1)增环:在尺寸链中,自身增大或减小,会使封闭环随之增大或减小的组成环,称为增环。
表示增环字母上面用--> 表示。
2)减环:在尺寸链中,自身增大或减小,会使封闭环反而随之减小或增大的组成环,称为减环。
表示减环字母上面用<-- 表示。
3)怎样确定增减环:用箭头方法确定,即凡是箭头方向与封闭环箭头方向相反的组成环为增环,相同的组成环为减环。
在图b所示尺寸链中,A1是增环,A2是减环。
4)传递系数ξi:表示组成环对封闭环影响大小的系数。
即组成环在封闭环上引起的变动量对组成环本身变动量之比。
对直线尺寸链而言,增环的ξi=1,减环的ξi=-1。
3.尺寸链的分类4.尺寸链的计算尺寸链计算有正计算、反计算和中间计算等三种类型。
已知组成环求封闭环的计算方式称作正计算;已知封闭环求各组成环称作反计算;已知封闭环及部分组成环,求其余的一个或几个组成环,称为中间计算。
尺寸链计算有极值法与统计法(或概率法)两种。
用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的。
用统计法解尺寸链则是运用概率论理论来求解封闭环尺寸与组成环尺寸之间关系的。
5.极值法解尺寸链的计算公式(4)封闭环的中间偏差(5)封闭环公差(6)组成环中间偏差Δi=(ES i+EI i)/2(7)封闭环极限尺寸(8)封闭环极限偏差6.竖式计算法口诀:封闭环和增环的基本尺寸和上下偏差照抄;减环基本尺寸变号;减环上下偏差对调且变号。

尺寸链的计算之答禄夫天创作一、尺寸链的基本术语:1.尺寸链——在机器装配或零件加工过程中,由相互连接的尺寸形成封闭的尺寸组,称为尺寸链。
如下图间隙A0与其它五个尺寸连接成的封闭尺寸组,形成尺寸链。
2.环——列入尺寸链中的每一个尺寸称为环。
如上图中的A0、A1、A2、A3、A4、A5都是环。
长度环用大写斜体拉丁字母A,B,C……暗示;角度环用小写斜体希腊字母α,β等暗示。
3.封闭环——尺寸链中在装配过程或加工过程后自然形成的一尺寸,称为封闭环。
如上图中A0。
封闭环的下角标“0”暗示。
4.组成环——尺寸链中对封闭环有影响的全部尺寸,称为组成环。
如上图中A1、A2、A3、A4、A5。
组成环的下角标用阿拉伯数字暗示。
5.增环——尺寸链中某一类组成环,由于该类组成环的变动引起封闭环同向变动,该组成环为增环。
如上图中的A3。
6.减环——尺寸链中某一类组成环,由于该类组成环的变动引起封闭环的反向变动,该类组成环为减环。
如上图中的A1、A2、A4、A5。
7.抵偿环——尺寸链中预先选定某一组成环,可以通过改变其大小或位置,使封闭环达到规定的要求,该组成环为抵偿环。
如下图中的L2。
二、尺寸链的形成为分析与计算尺寸链的方便,通常按尺寸链的几何特征,功能要求,误差性质及环的相互关系与相互位置等分歧观点,对尺寸链加以分类,得出尺寸链的分歧形式。
1.长度尺寸链与角度尺寸链①长度尺寸链——全部环为长度尺寸的尺寸链,如图1 ②角度尺寸链——全部环为角度尺寸的尺寸链,如图32.装配尺寸链,零件尺寸链与工艺尺寸链①装配尺寸链——全部组成环为分歧零件设计尺寸所形成的尺寸链,如图4②零件尺寸链——全部组成环为同一零件设计尺寸所形成的尺寸链,如图5③工艺尺寸链——全部组成环为同一零件工艺尺寸所形成的尺寸链,如图6。
工艺尺寸指工艺尺寸,定位尺寸与基准尺寸等。
装配尺寸链与零件尺寸链统称为设计尺寸链。
3.基本尺寸链与派生尺寸链①基本尺寸链——全部组成环皆直接影响封闭环的尺寸链,如图7中尺寸链β。

尺寸链的计算方法
尺寸链是指产品设计、制造、装配和质量控制过程中的一种重要工具,它可以
帮助我们更好地理解产品的尺寸要求,保证产品的质量和性能。
在实际工程中,尺寸链的计算方法是非常关键的,下面我们将详细介绍尺寸链的计算方法。
首先,我们需要明确尺寸链的定义。
尺寸链是指产品各零部件之间的尺寸关系,包括公差、配合、间隙等内容。
在产品设计阶段,我们需要根据产品的功能要求和制造工艺来确定尺寸链,以保证产品的装配性和性能。
其次,尺寸链的计算方法主要包括以下几个步骤,确定尺寸链的起始尺寸、确
定尺寸链的公差、计算尺寸链的累积公差、分析尺寸链的影响。
首先,我们需要根据产品的功能要求和装配工艺确定尺寸链的起始尺寸,即各零部件的基准尺寸。
然后,根据国家标准或行业标准确定各零部件的公差,包括尺寸公差、形位公差等。
接下来,我们需要计算尺寸链的累积公差,即各零部件在装配过程中的尺寸偏差累积值。
最后,我们需要分析尺寸链对产品性能和装配性的影响,以确定是否满足产品设计要求。
在实际工程中,尺寸链的计算方法需要结合产品的具体情况和制造工艺来进行。
我们需要根据产品的功能要求和装配工艺来确定尺寸链的起始尺寸和公差,同时考虑产品的材料特性和加工工艺,以保证产品的质量和性能。
总之,尺寸链的计算方法是产品设计和制造过程中的重要内容,它可以帮助我
们更好地理解产品的尺寸要求,保证产品的质量和性能。
在实际工程中,我们需要根据产品的具体情况和制造工艺来确定尺寸链,以保证产品的装配性和性能。
希望本文对您有所帮助,谢谢阅读!。
关于尺寸链的简单计算方法之一:坚式法。
1、先确定尺寸链中的组成:增环、减环、封闭环,并画出尺寸链图。
(有一定的难度)
2、根据以下三点把相关的数据填入下表:
a、增环的尺寸及偏差不变,照抄入表格内
b、减环的尺寸及偏差要变号,并上下偏差对调,填入相应表格内。
(此步最重要)
c、封闭环等于增减环尺寸、偏差的代数和。
例如,右图是一个定位套零件,图中已标注了A0及A1的尺寸及偏差,若直接按此图来加工时,A0尺寸不便直接测量,但可通过加工便于测量的尺寸A2来间接保证A0的尺寸。
分析可知A1为增环,A2为减环,A0为封闭环,并画出尺寸链图。
分别
25-X=10,可解得X=15
0-b=0.1,可解得b=-0.1
-0.05-a=-0.1,可解得a=0.05
即尺寸A2=15
此方法可用于计算增环、减环、封闭环的尺寸及其及偏差。
相关概念:
1、封闭环是指尺寸链中在加工或装配过程中最后形成的一环,它的大小是由组成环间接保证的。
如A0。
2、组成环,它包括增环、减环。
a、增环若该环的变动将会引起封闭环的同向变动(同向变动是指该环增大时封闭环也增大,该环减小时封闭环也减小)
b、减环若该环的变动将会引起封闭环的反向变动(反向变动是指该环增大时封闭环减小,该环减小时封闭环增大)
A0
A1
A2
X
a
b
1.零件图
2.尺寸链图
+0.05
-0.1
3.最后可得出便于加工的图PDF created with pdfFactory Pro trial version 。
式中,—尺寸链中第j个组成环的标准偏差。
如果各组成环的实际尺寸都为正态分布,并且分布范围与公差带宽度一致,分布中心与公差带中心重合,见图8-8,则封闭环的实际尺寸也服从正态分布,各环公差与标准偏差关系如下
T0 = 6σ0
T j= 6
将以上两式代入(8-9)式,得
(8—10) (8—10)式表明:封闭环公差等于所有组成环公差的方和根。
由图8-8可见,各组成环的中间偏差为其上、下偏差的平均值。
封闭环的中间偏差∆0与组成环的中间偏差∆j分别为
∆0 =
∆j =
各组成环的中心尺寸为极限尺寸的平均值。
封闭环的中间尺寸A0中为封闭环的基本尺寸与其中间偏差之和:
A0中 = A0+ ∆0 (8-11) 组成环中间尺寸A j中为组成环的基本尺寸与中间偏差之和:
A j中 = A j+ ∆j(8-12)
(8-4)和(8-5)式相加后取平均值可得
-13) 即:封闭环中间尺寸等于所有增环的中间尺寸之和减去所有减环的中间尺寸之和。
将上述公式整理得:
(8-14) 即:封闭环中间偏差等于所有增环的中间偏差之和减去所有减环的中间偏差之和。
如果组成环的实际尺寸不服从正态分布,而是其它分布,或者组成环分布中心偏离公差带中心,那么本节所述公式应加以修正,详见有关书籍。
用大数互换法解尺寸链的步骤基本上与极值法相同。
但在计算封闭环和组成环的上、下偏差时,要先算出它们的中间偏差。
,B2=70 0 -0.03,B0 = 四、例题:在上节课图所示的齿轮轴装配图中:B1=100+0.14
0.02—0.20,求垫片轴向尺寸B3为多少?
列式计算
∵ B0max = B1max - (B2min + B3min)
∴ B3min = B1max - B2min – B0max
=100.14-69.97-0.2
= 29.97mm
同理:B3max = B1min- B2max- B0min
= 100- 70-0.02
= 29.98 mm。
结论:垫片轴向尺寸B3为 30-0.02
-0.03。