2020年中考复习专题2相似三角形存在性问题

中考压轴题相似三角形存在性问题数学因运动而充满活力，数学因变化而精彩纷呈．动态题是近年来中考的的一个热点问题，以运动的观点探究几何图形的变化规律问题，称之为动态几何问题，随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题，就其运动对象而言，有点动、线动、面动三大类，就其运动形式而言，有轴对称（翻折）、平移、旋转（中心对称、滚动）等，就问题类型而言，有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等．解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况．以动态几何问题为基架而精心设计的考题，可谓璀璨夺目、精彩四射．动态几何形成的存在性问题是动态几何中的基本类型，包括等腰（边）三角形存在问题；直角三角形存在问题；平行四边形存在问题；矩形、菱形、正方形存在问题；梯形存在问题；全等三角形存在问题；相似三角形存在问题；其它存在问题等．本专题原创编写动点形成的全等、相似三角形存在性问题模拟题．在中考压轴题中，线面动形成的全等、相似三角形存在性问题的重点和难点在于应用数形结合的思想准确地进行分类．原创模拟预测题1．已知，如图①，在▱ABCD 中，AB=3cm ，BC=5cm ，AC ⊥AB ，△ACD 沿AC 的方向匀速平移得到△PNM ，速度为1cm/s ；同时，点Q 从点C 出发，沿CB 方向匀速移动，速度为1cm/s ，当△PNM 停止平移时，点Q 也停止移动，如图②，设移动时间为t （s ）（0＜t ＜4），连接PQ ，MQ ，MC ，解答下列问题：（1）当t 为何值时，PQ ∥MN ？（2）设△QMC 的面积为y （cm2），求y 与x 之间的函数关系式；（3）是否存在某一时刻t ，使S △QMC ：S 四边形ABQP=1：4？若存在，求出t 的值；若不存在，请说明理由．（4）是否存在某一时刻t ，使PQ ⊥MQ ？若存在，求出t 的值；若不存在，请说明理由．【答案】（1）920=t ；（2）236105y t t =-+（0＜t ＜4）；（3）t=2；（4）23=t ． 【解析】 试题分析：（1）根据勾股定理求出AC ，根据PQ ∥AB ，得出CB CQ CA CP =，544t t =-，求解即可；（2）过点P 作PD ⊥BC 于D ，根据△CPD ∽△CBA ，得出453t PD -=，求出PD=1235t -，再根据S △QMC=S △QPC ，得出y=S △QMC=12QC•PD ，再代入计算即可； （3）根据S △QMC ：S 四边形ABQP=1：4，得出S △QPC ：S △ABC=1：5，代入得出（236105t t -+）：6=1：5，再计算即可； （4）根据PQ ⊥MQ 得出△PDQ ∽△MQP ，得出2PQ =MP•DQ ，根据勾股定理得出22PD DQ +=MP•DQ ，再分别代入得出59165)5916()5312(22t t t -⨯=-+-，求出t 即可．（4）若PQ ⊥MQ ，则∠PQM=∠PDQ ，∵∠MPQ=∠PQD ，∴△PDQ ∽△MQP ，∴DQ PQ PQ PM =，∴2PQ =MP•DQ ，∴22PD DQ +=MP•DQ ，∵CD=1645t -，∴DQ=CD ﹣CQ=1645t t --=1695t -，∴59165)5916()5312(22t t t -⨯=-+-，∴整理得0322=-t t ，解得10t =（舍去），232t =，∴23=t 时，PQ ⊥MQ ．考点：相似形综合题；动点型；存在型；综合题；压轴题．原创模拟预测题2．如图1，在△ABC 中，∠C=90°，点D 在AC 上，且CD ＞DA ，DA=2，点P ，Q 同时从点D 出发，以相同的速度分别沿射线DC 、射线DA 运动，过点Q 作AC 的垂线段QR，使QR=PQ，连接PR，当点Q到达点A时，点P，Q同时停止运动．设PQ=x，△PQR与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中087x<≤，87x m<≤时，函数的解析式不同）．（1）填空：n的值为；（2）求S关于x的函数关系式，并写出x的取值范围．【答案】（1）3249；（2）228(0)7256328(4)412545457xx x xxS<≤-+⎧⎪⎪=⎨-<≤⎪⎪⎩．【解析】试题分析：（1）当x=78时，△PQR与△ABC重叠部分的面积就是△PQR的面积，然后根据PQ=78，QR=PQ，求出n的值是多少即可．（2）首先根据S关于x的函数图象，可得S关于x的函数表达式有两种情况：①当87x<≤时，求出S关于x的函数关系式，判断出当点Q点运动到点A时，x=2AD=4，据此求出m=4；②当847x<≤时，S关于x的函数关系式即可．试题解析：（1）如图1，当x=78时，△PQR与△ABC重叠部分的面积就是△PQR的面积，∵PQ=78，QR=PQ，∴QR=78，∴n=S=21(287)⨯=3249；综上，可得：228 (0)7256328(4)412545457xx x xxS<≤-+⎧⎪⎪=⎨-<≤⎪⎪⎩．考点：动点问题的函数图象；动点型；分类讨论；分段函数；综合题；压轴题．原创模拟预测题3．如图，在平面直角坐标系中，抛物线23y ax bx=++x轴交于A（﹣3，0），B（1，0）两点．与y轴交于点C，点D与点C关于抛物线的对称轴对称．（1）求抛物线的解析式，并直接写出点D 的坐标；（2）如图1，点P 从点A 出发，以每秒1个单位长度的速度沿A→B 匀速运动，到达点B 时停止运动．以AP 为边作等边△APQ （点Q 在x 轴上方），设点P 在运动过程中，△APQ 与四边形AOCD 重叠部分的面积为S ，点P 的运动时间为t 秒，求S 与t 之间的函数关系式；（3）如图2，连接AC ，在第二象限内存在点M ，使得以M 、O 、A 为顶点的三角形与△AOC 相似．请直接写出所有符合条件的点M 坐标．【答案】（1）2323333y x x =--+ D （﹣2，3）；（2）223 (02)3 3 (23)3113 3 (34)2t t t t t ≤≤-<≤⎪+<≤⎪⎩；（3）M （﹣3，3或（﹣3，33或（94-，33）或（34-，33）． 【解析】试题分析：（1）把A 、B 的坐标代入即可求得函数解析式即可，由点D 与C 对称求得点D 坐标即可；（2）由特殊角的三角函数值得出∠DAP=60°，则点Q 一直在直线AD 上运动，分别探讨当点P 在线段AO 上；点Q 在AD 的延长线上，点P 在线段OB 上以及点Q 在AD 的延长线上，点P 在线段OB 上时的重叠面积，利用三角形的面积计算公式求得答案即可；（3）由于3OA=3，OA ⊥OC ，则△OAC 是含30°的直角三角形，分两种情况探讨：当△AMO 以∠AMO 为直角的直角三角形时；当△AMO 以∠OAM 为直角的直角三角形时；得出答案即可．试题解析：（1）∵抛物线23y ax bx =++经过A （﹣3，0），B （1，0）两点，∴933030a b a b ⎧-+=⎪⎨++=⎪⎩，解得：33233a b ⎧=-⎪⎪⎨⎪=-⎪⎩，∴抛物线解析式为2323333y x x =--+则D 点坐标为（﹣2，3）；②当2＜t≤3时，如图：此时点Q 在AD 的延长线上，点P 在OA 上，设QP 与DC 交于点H ，∵DC ∥AP ，∴∠QDH=∠QAP=∠QHD=∠QPA=60°，∴△QDH 是等边三角形，∴S=S △QAP ﹣S △QDH ，∵QA=t ，∴S △QAP=234t ，∵QD=t ﹣2，∴S △QDH=232)4t -，∴S=2233(2)44t --33t③当3＜t≤4时，如图：此时点Q在AD的延长线上，点P在线段OB上，设QP与DC交于点E，与OC交于点F，过点Q作AP的垂涎，垂足为G，∵OP=t﹣3，∠FPO=60°，∴OF=OP•tan60°=3（t﹣3），∴S△FOP=132⨯t﹣3）（t﹣3）=23(3)t-，∵S=S△QAP﹣S△QDE﹣S△FOP，S△QAP﹣S△QDE=33t-．∴2333(3)2t t---=23114332t t-+-．综上所述，S与t之间的函数关系式为S=223(02)3 3 (23)31143 3 (34)2t tt tt t t⎧≤≤⎪⎪⎪-<≤⎨⎪-+-<≤⎪⎩；（3）∵OC=3，OA=3，OA⊥OC，则△OAC是含30°的直角三角形．①当△AMO以∠AMO为直角的直角三角形时；如图：过点M2作AO的垂线，垂足为N，∵∠M2AO=30°，AO=3，∴M2O=32，又∵∠OM2N=M2AO=30°，∴ON=12OM2=34，M2N=3ON=33，∴M2的坐标为（34-，33），同理可得M1的坐标为（94-，33）；②当△AMO以∠OAM为直角的直角三角形时；如图：∵以M、O、A为顶点的三角形与△OAC相似，∴OAAM3AMOA3OA=3，∴3或AM=33AM⊥OA，且点M在第二象限，∴点M的坐标为（﹣33）或（﹣3，33．综上所述，符合条件的点M的所有可能的坐标为（﹣3，3），（﹣3，33，（94-，33），（34-，33）．考点：二次函数综合题；相似三角形综合题；分段函数；分类讨论；动点型；相似三角形的判定；综合题；压轴题．。

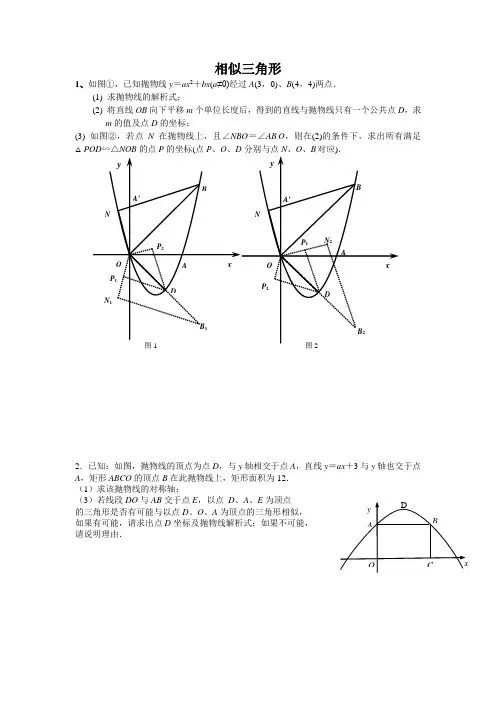
相似三角形1、如图①，已知抛物线y ＝ax 2＋bx (a ≠0)经过A (3，0)、B (4，4)两点．(1) 求抛物线的解析式；(2) 将直线OB 向下平移m 个单位长度后，得到的直线与抛物线只有一个公共点D ，求m 的值及点D 的坐标；(3) 如图②，若点N 在抛物线上，且∠NBO ＝∠AB O ，则在(2)的条件下，求出所有满足△B2．已知：如图，抛物线的顶点为点D ，与y 轴相交于点A ，直线y ＝ax ＋3与y 轴也交于点A ，矩形ABCO 的顶点B 在此抛物线上，矩形面积为12． （1）求该抛物线的对称轴；（3）若线段DO 与AB 交于点E ，以点 D 、A 、E 为顶点的三角形是否有可能与以点D 、O 、A 为顶点的三角形相似，如果有可能，请求出点D 坐标及抛物线解析式；如果不可能， 请说明理由．3、如图，直线AB 交x 轴于点B （4，0），交y 轴于点A （0，4），直线DM ⊥x 轴正半轴于点M ，交线段AB 于点C ，DM=6，连接DA ，∠DAC=90°． （1）直接写出直线AB 的解析式； （2）求点D 的坐标；（3）若点P 是线段MB 上的动点，过点P 作x 轴的垂线，交AB 于点F ，交过O 、D 、B 三点的抛物线于点E ，连接CE ．是否存在点P ，使△BPF 与△FCE 相似？若存在，请求出点P 的坐标；若不存在，请说明理由．3．如图，已知点A (-2，4) 和点B (1，0)都在抛物线22y mx mx n =++上．（1）求m 、n ；（2）向右平移上述抛物线，记平移后点A 的对应点为A ′，点B 的对应点为B ′，若四边形 A A ′B ′B 为菱形，求平移后抛物线的表达式； （3）记平移后抛物线的对称轴与直线AB ′ 的 交点为点C ，试在x 轴上找点D ，使得以点 B ′、C 、D 为顶点的三角形与ABC △相似．1、解：(1) ∵ 抛物线y ＝ax 2＋bx (a ≠0)经过点A (3，0)、B (4，4)．∴⎨⎧9a ＋3b ＝016a ＋4b ＝4，解得：⎨⎧a ＝1b ＝－3．∴ 抛物线的解析式是y ＝x 2－3x ．(2) 设直线OB 的解析式为y ＝k 1x ，由点B (4，4)，得：4＝4k 1，解得k 1＝1．∴ 直线OB 的解析式为y ＝x ．∴ 直线OB 向下平移m 个单位长度后的解析式为：y ＝x －m ．∵ 点D 在抛物线y ＝x 2－3x 上．∴ 可设D (x ，x 2－3x )．又点D 在直线y ＝x －m 上，∴ x 2－3x ＝x －m ，即x 2－4x ＋m ＝0．∵ 抛物线与直线只有一个公共点，∴ △＝16－4m ＝0，解得：m ＝4． 此时x 1＝x 2＝2，y ＝x 2－3x ＝－2，∴ D 点坐标为(2，－2)．(3) ∵ 直线OB 的解析式为y ＝x ，且A (3，0)，∴ 点A 关于直线OB 的对称点A'的坐标是(0，3)．设直线A'B 的解析式为y ＝k 2x ＋3，过点B (4，4)，∴ 4k 2＋3＝4，解得：k 2＝14．∴ 直线A'B 的解析式是y ＝14x ＋3．∵ ∠NBO ＝∠ABO ，∴ 点N 在直线A'B 上，∴ 设点N (n ，14n ＋3)，又点N 在抛物线y ＝x 2－3x 上， ∴ 14n ＋3＝n 2－3n ， 解得：n 1＝－34，n 2＝4(不合题意，会去)，∴ 点N 的坐标为(－34，4516)．方法一：如图1，将△NOB 沿x 轴翻折，得到△N 1OB 1，则N 1(－34，－4516)，B 1(4，－4)，∴ O 、D 、B 1都在直线y ＝－x 上．∵ △P 1OD ∽△NOB ，∴ △P 1OD ∽△N 1OB 1，∴ OP 1ON 1＝OD OB 1＝12，∴ 点P 1的坐标为(－38，－4532)．将△OP 1D 沿直线y ＝－x 翻折，可得另一个满足条件的点P 2(4532，38)．综上所述，点P 的坐标是(－38，－4532)或(4532，38)．方法二：如图2，将△NOB 绕原点顺时针旋转90°，得到△N 2OB 2，则N 2(4516，34)，B 2(4，－4)， ∴ O 、D 、B 2都在直线y ＝－x 上．∵ △P 1OD ∽△NOB ，∴ △P 1OD ∽△N 2OB 2，∴ OP 1ON 2＝OD OB 2＝12，∴ 点P 1的坐标为(4532，38)．将△OP 1D 沿直线y ＝－x 翻折，可得另一个满足条件的点P 2(－38，－4532)．综上所述，点P 的坐标是(－38，－4532)或(4532，38)．点坐标． ，解得，所以，直线，所以，抛物线解析式为4将E （x ，x ）代入抛物线y=﹣x （x ﹣4）中，得x=﹣x （x ﹣4），解得x=0或，，则PE=MC=2，将E （x ，2）代入抛物线y=﹣x （x ﹣4）中，得2=﹣x （x ﹣4），x=，）或（的形状，如图1，在平面直角坐标系xOy 中，顶点为M 的抛物线y ＝ax 2＋bx （a ＞0）经过点A 和x 轴正半轴上的点B ，AO ＝BO ＝2，∠AOB ＝120°．（1）求这条抛物线的表达式；（2）连结OM ，求∠AOM 的大小；（3）如果点C 在x 轴上，且△ABC 与△AOM 相似，求点C 的坐标．如图1，已知抛物线的方程C 1：1(2)()y x x m m =-+- (m ＞0)与x 轴交于点B 、C ，与y 轴交于点E ，且点B 在点C 的左侧．（1）若抛物线C 1过点M (2, 2)，求实数m 的值； （2）在（1）的条件下，求△BCE 的面积；（3）在（1）的条件下，在抛物线的对称轴上找一点H ，使得BH ＋EH 最小，求出点H 的坐标；（4）在第四象限内，抛物线C 1上是否存在点F ，使得以点B 、C 、F 为顶点的三角形与△BCE 相似？若存在，求m 的值；若不存在，请说明理由．。

相似三角形的存在性问题解题策略专题攻略相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验，如例题1、2、3、4．应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等，如例题6．应用判定定理3解题不多见，如例题5，根据三边对应成比例列连比式解方程(组)．例题解析例❶如图1-1,抛物线y=1x2-3x+4与X轴交于A、B两点(A点在B点左侧),与y轴交于点C.动82直线EF(EF//x轴)从点C开始，以每秒1个单位的速度沿y轴负方向平移，且分别交y轴、线段BC于E、F两点，动点P同时从点B出发，在线段0B上以每秒2个单位的速度向原点0运动.是否存在t,使得△匕卩卩与厶ABC相似.若存在，试求出t的值；若不存在，请说明理由.图1-1【解析】ABP卩与厶ABC有公共角ZB，那么我们梳理两个三角形中夹ZB的两条边.△ABC是确定的.由y=x2-x+4，可得A(4,0)、B(&0)、C(0,4).782于是得到BA=4,BC=4*5.还可得到C E=C0=1.EF OB2△BPF中，BP=21,那么BF的长用含t的式子表示出来，问题就解决了. 在RtAEFC中，CE=t,EF=21,所以CF=^5t.因此BF=处5-呂二*；5(4-1).于是根据两边对应成比例，分两种情况列方程BABP ①当—时，BCBF42t44_—.解得t—（如图1-2）. 4冒55（4-1）3BABF ②当—时，BCBP4—〔5（4-1）.解得1—20（如图1-3）. 4f5217得顶点M(1,-图1-2 图1-3例❷如图2-1,在平面直角坐标系中，顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,ZAOB=120°.(1)这条抛【解析】AABC与AAOM中相等的一组角在哪里呢?本题由简到难，层层深入.第(1)题求出抛物线的解析式，得到顶点M的坐标，为第(2)题求ZAOM的大小作铺垫；求得了ZAOM的大小，第(3)题暗示了要在△ABC中寻找与ZAOM相等的角.(1)如图2-2,过点A作AH丄y轴，垂足为H.容易得到A(-1,3).再由A(-1,J3)、B(2,0)两点，可求得抛物线的解析式为y二辜x2-睾x.⑵由y吕x2一斗x召(x-1)2-斗,v33(3)由A (-1,\：'3)、B(2,0),可得ZABO=30°. 因此当点C 在点B 右侧时，ZABC=ZA0M=150°. 所以△ABC 与AAOM 相似，存在两种情况：① 当燮=_°A 仝时，BC =BA ==2.此时C(4,0)(如图2-3).BCOM J3弋3 BC OA —② 当==时，BC =x/3BA =\3x 2\；3=6.此时C (8,0)(如图2-4).BAOM图2-3.图2-4例❸如图3-1,抛物线y=ax 2+bx —3与x 轴交于A(l,0)、B(3,0)两点，与y 轴交于点D,顶点为C.(1)求此抛物线的解析式；(2)在x 轴下方的抛物线上是否存在点M,过M 作MN 丄x 轴于点N,使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，求出点M 的坐标；若不存在，请说明理由.图3-1【解析】AAMN 是直角三角形，因此必须先证明△BCD 是直角三角形.一般情况下，根据直角边对应成比例分两种情况列方程.所以 tan ZBOM=.所以ZBOM=30。

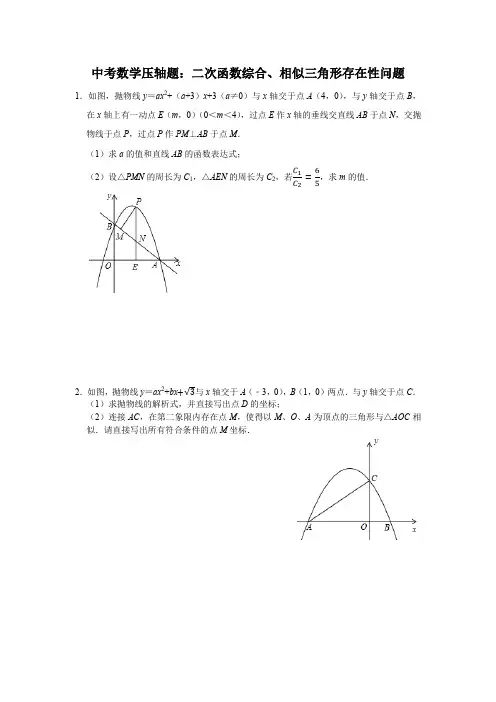
中考数学压轴题：二次函数综合、相似三角形存在性问题1．如图，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若C1C2=65，求m的值．2．如图，抛物线y＝ax2+bx+√3与x轴交于A（﹣3，0），B（1，0）两点．与y轴交于点C．（1）求抛物线的解析式，并直接写出点D的坐标；（2）连接AC，在第二象限内存在点M，使得以M、O、A为顶点的三角形与△AOC相似．请直接写出所有符合条件的点M坐标．3．如图，二次函数y＝ax2+bx﹣3的图象与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．该抛物线的顶点为M．（1）求该抛物线的解析式；（2）判断△BCM的形状，并说明理由；（3）探究坐标轴上是否存在点P，使得以点P、A、C为顶点的三角形与△BCM相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．4．如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y＝x﹣2交于B，C两点．（1）求抛物线的解析式及点C的坐标；（2）求证：△ABC是直角三角形；（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．5．如图，抛物线y＝ax2+bx﹣1（a≠0）经过A（﹣1，0），B（2，0）两点，与y轴交于点C．（1）求抛物线的解析式及顶点D的坐标；（2）点P在抛物线的对称轴上，当△ACP的周长最小时，求出点P的坐标；（3）点N在抛物线上，点M在抛物线的对称轴上，是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似？若存在，请求出所有符合条件的点N的坐标；若不存在，请说明理由．6．如图，已知抛物线y=13x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．（1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP 的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．7．如图，已知抛物线与x轴交于A（﹣1，0），B（4，0），与y轴交于C（0，﹣2）．（1）求抛物线的解析式；（2）D是C关于x轴的对称点，P是抛物线上的一点，当△PBD与△AOC相似时，求符合条件的P点的坐标．8．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（4，0）两点，与y轴相交于点C，连接BC，点P为抛物线上一动点，过点P作x轴的垂线l，交直线BC于点G，交x轴于点E．（1）求抛物线的表达式；（2）当P位于y轴右边的抛物线上运动时，过点C作CF⊥直线l，F为垂足，当点P 运动到何处时，以P，C，F为顶点的三角形与△OBC相似？并求出此时点P的坐标；9．如图，已知二次函数y ＝﹣x 2+bx +c （b ，c 为常数）的图象经过点A （3，1），点C （0，4），顶点为点M ，过点A 作AB ∥x 轴，交y 轴于点D ，交该二次函数图象于点B ，连接BC ．（1）求该二次函数的解析式及点M 的坐标；（2）点P 是直线AC 上的动点，若点P ，点C ，点M 所构成的三角形与△BCD 相似，请直接写出所有点P 的坐标．10．如图，抛物线y ＝ax 2+bx 经过两点A （﹣1，1），B （2，2）．过点B 作BC ∥x 轴，交抛物线于点C ，交y 轴于点D ．（1）求此抛物线对应的函数表达式及点C 的坐标；（2）若抛物线上存在点M ，使得△BCM 的面积为72，求出点M 的坐标； （3）连接OA 、OB 、OC 、AC ，在坐标平面内，求使得△AOC 与△OBN 相似（边OA 与边OB 对应）的点N 的坐标．11．如图1，抛物线y＝ax2+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．（1）求抛物线的解析式，并写出其顶点B的坐标；（2）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．。

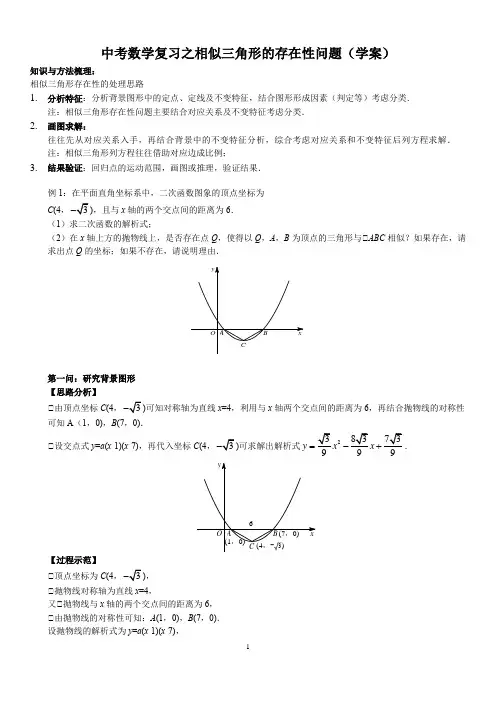
中考数学复习之相似三角形的存在性问题（学案）知识与方法梳理：相似三角形存在性的处理思路1. 分析特征：分析背景图形中的定点、定线及不变特征，结合图形形成因素（判定等）考虑分类．注：相似三角形存在性问题主要结合对应关系及不变特征考虑分类．2. 画图求解：往往先从对应关系入手，再结合背景中的不变特征分析，综合考虑对应关系和不变特征后列方程求解． 注：相似三角形列方程往往借助对应边成比例；3. 结果验证：回归点的运动范围，画图或推理，验证结果．例1：在平面直角坐标系中，二次函数图象的顶点坐标为 C (4，，且与x 轴的两个交点间的距离为6． （1）求二次函数的解析式；（2）在x 轴上方的抛物线上，是否存在点Q ，使得以Q ，A ，B 为顶点的三角形与△ABC 相似？如果存在，请求出点Q 的坐标；如果不存在，请说明理由．第一问：研究背景图形 【思路分析】△由顶点坐标C (4，)可知对称轴为直线x =4，利用与x 轴两个交点间的距离为6，再结合抛物线的对称性可知A （1，0)，B (7，0)．△设交点式y =a (x -1)(x -7)，再代入坐标C (4，可求解出解析式2y x =-+．【过程示范】△顶点坐标为C (4，)， △抛物线对称轴为直线x =4，又△抛物线与x 轴的两个交点间的距离为6， △由抛物线的对称性可知：A (1，0)，B (7，0)． 设抛物线的解析式为y =a (x -1)(x -7)，将C (4，)代入可得，a = △所求解析式为2y x x =． 第二问：相似三角形的存在性 【思路分析】相似三角形存在性问题也是在存在性问题的框架下进行的：△分析特征：先研究定点、动点，其中A 、B 、C 为定点，点Q 为抛物线上的动点；进一步研究此△ABC ，发现其中AC=BC ；构造辅助线：CD 垂直于x 轴，能够计算出△BAC =30°，△ACB =30°；再考虑研究△QAB ，固定线段为AB ，并且由于点Q 在x 轴上方的抛物线上，所以△QAB 为钝角（填“钝角”或“直角”）三角形．△画图求解：先考虑点Q 在抛物线对称轴右侧的情况，此时△ABQ 为钝角，要想使△ABC 与△ABQ 相似，则需要△ABQ =120°，且AB=BQ ．求解时，可根据△ABQ =120°，AB =BQ =6来求出Q 点坐标．同理，考虑点Q 在抛物线对称轴左侧时的情况．△结果验证：考虑点Q 还要在抛物线上，将点Q 代入抛物线解析式验证． 【过程示范】存在点Q 使得△QAB 与△ABC 相似．由抛物线对称性可知，AC =BC ，过点C 作CD △x 轴于D ， 则AD =3，CD在Rt△ACD 中，tan△DAC，△△BAC =△ABC =30°，△ACB =120°． △当△ACB △△ABQ 1时， △ABQ 1=120°且BQ 1=AB =6． 过点Q 1作Q 1E △x 轴，垂足为E ， 则在Rt△BQ 1E 中，BQ 1=6，△Q 1BE =60°， △Q 1E =BQ 1·sin60°=62⨯=BE =3， △E (10，0)，Q 1(10，． 当x =10时，y= △点Q 1在抛物线上．△由抛物线的对称性可知，还存在AQ 2=AB ， 此时△Q 2AB △△ACB ，点Q 2的坐标为(-2，． 综上，Q 1(10，，Q 2(-2，．练习题1. 如图，抛物线2110833y x x =-+-经过A ，B ，C 三点，BC △OB ，AB =BC ，过点C 作CD ⊥x 轴于点D ．点M是直线AB 上方的抛物线上一动点，作MN ⊥x 轴于点N ，若△AMN 与△ACD 相似，则点M 的坐标为_____________________________．OB CDAxy2. 如图，已知抛物线234y x bx c =++与坐标轴交于A ，B ，C 三点，点A 的坐标为(1，0)，过点C 的直线334y x t=-与x 轴交于点Q ，点P 是线段BC 上的一个动点，过P 作PH △OB 于点H ．若PB 5t ，且0＜t ＜1．（1）点C 的坐标是____________，b _______，c ______． （2）求线段QH 的长（用含t 的代数式表示）．（3）依点P 的变化，是否存在t 的值，使以P ，H ，Q 为顶点的三角形与△COQ 相似？若存在，求出所有符合条件的t 值；若不存在，说明理由．A BCOHP QxyyxO CB A3. 如图，抛物线213222y x x =-++与x 轴交于A ，B 两点，与y 轴交于点C ，点D (1，m )在抛物线上，直线y =-x -1与抛物线交于A ，E 两点，点P 在x 轴上，且位于点B 的左侧，若以P ，B ，D 为顶点的三角形与△ABE 相似，则点P 的坐标为__________________________________．4. 如图，已知抛物线过点A (0，6)，B (2，0)，C (7，52)．（1）求抛物线的解析式．（2）若D 是抛物线的顶点，E 是抛物线的对称轴与直线AC 的交点，F 与E 关于D 对称．求证：△CFE =△AFE ． （3）在y 轴上是否存在这样的点P ，使△AFP 与△FDC 相似？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．5.如图，抛物线y=ax2+bx经过两点A(-1，1)，B(2，2)．过点B作BC△x轴，交抛物线于点C，交y轴于点D．连接OA，OB，OC，AC，点N在坐标平面内，且△AOC与△OBN相似（边OA与边OB对应），则点N的坐标为_____________________________________．6.如图，抛物线y=-x2+4与x轴交于A，B两点，与y轴交于点C，连接AC．点P是第一象限内抛物线上的一个动点，过点P作x轴的垂线，垂足为D．是否存在以P，O，D为顶点的三角形与△OAC相似？若存在，请求出点P的坐标；若不存在，请说明理由．7.如图，已知抛物线y=x2-1与x轴交于A，B两点，与y轴交于点C，过点A作AP△CB交抛物线于点P．（1）求A，B，C三点的坐标．（2）在x轴上方的抛物线上是否存在一点M，过点M作MG△x轴于点G，使以A，M，G为顶点的三角形与△PCA 相似？若存在，请求出点M的坐标；若不存在，请说明理由．8.如图，抛物线y=ax2+b与x轴交于点A，B，且点A的坐标为(1，0)，与y轴交于点C(0，1)．（1）求抛物线的解析式，并求出点B的坐标．（2）过点B作BD△CA交抛物线于点D，在x轴上点A的左侧是否存在点P，使以P，A，C为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由．9. 如图，抛物线经过A (4，0)，B (1，0)，C (0，-2)三点．（1）求抛物线的解析式．（2）P 是抛物线上一动点，过点P 作PM △x 轴，垂足为M ，是否存在点P ，使得以A ，P ，M 为顶点的三角形与△OAC 相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由．参考答案1. 2. （1）(0，-3)，，-3；（2）；（3）存在，或． 3. 4. （1）；（3）． 5. N 1(3，4)，N 2(4，3)，N 3(-2，-1)，N 4(-1，-2)6.存在，1P ，2(12P --+．7.（1）A (-1，0)，B (1，0)，C (0，-1)；（2）存在，M 1(-2，3)，M 2(4，15)，347()39M ，． 1257111()()2424M M -，，，94-148 0218 4 12t t QH t t ⎧-<<⎪⎪=⎨⎪-<<⎪⎩（）（）73225321121322(0)(0)75P P -，，，21462y x x =-+1241(0)(02)2P P --，，，8.（1）y =-x 2+1，B (-1，0)；（2）存在，11(0)3P ，，P 2(-2，0)． 9.（1）215222y x x =-+-；（2）存在，P 1(0，-2)，P 2(-3，-14)，P 3(2，1)，P 4(5，-2)．。

中考数学压轴题分析：相似三角形的存在性问题几何图形的存在性问题是中考常见的问题。

本文内容选自2020年广东省中考数学压轴题，考查相似三角形的存在性问题，难度不小。

一个三角形形状大小确定，另外一个三角形有两个动点。

具体请看下面内容。

【中考真题】（2020·广东）如图，抛物线与轴交于，两点，点，分别位于原点的左、右两侧，，过点的直线与轴正半轴和抛物线的交点分别为，，．（1）求，的值；（2）求直线的函数解析式；（3）点在抛物线的对称轴上且在轴下方，点在射线上．当与相似时，请直接写出所有满足条件的点的坐标．【分析】题（1）利用待定系数法求解析式，根据BO=3AO=3，得出点，点坐标，代入求抛物线解析式。

题（2）求BD的解析式，需要确定点D的坐标。

由于题目已知BC与CD的比例关系，可以考虑过点D作x轴的垂线，得到一个A字型的相似，求出点D的横坐标，代入二次函数的解析式，然后即可得到结论。

当然，如果先设直线BD的解析式为y=kx－3k，联立二次函数的解析式，得到一元二次方程的两根x1与x2的关系即可求出k的值。

题（3）中需要确定与△ABD相似的△BPQ。

由于A、B、D三点的位置的固定的，坐标也是确定的。

那么形状与大小就确定了。

先求出3边长度，且易得∠BAD为钝角。

而∠PBQ不可能为钝角，所以只需要分两种情况讨论即可：①点B与点B对应；②点B与点D对应。

两种情况中边的比例又有两种情况，因此分为4种情况讨论。

设PQ的坐标，然后根据比例关系得出结论。

【答案】解：（1），点，点，抛物线解析式为：，，；（2）如图1，过点作于，，，，，，，点横坐标为，点坐标为，，设直线的函数解析式为：，由题意可得：，解得：，直线的函数解析式为；（3）点，点，点，，，，，对称轴为直线，直线与轴交于点，点，，，，如图2，过点作于，，，，，如图，设对称轴与轴的交点为，即点，若，，，，，当，，，点，；当，，，点，；若，，，当，，，点，；当，，，点，；综上所述：满足条件的点的坐标为，或，或，或，．。

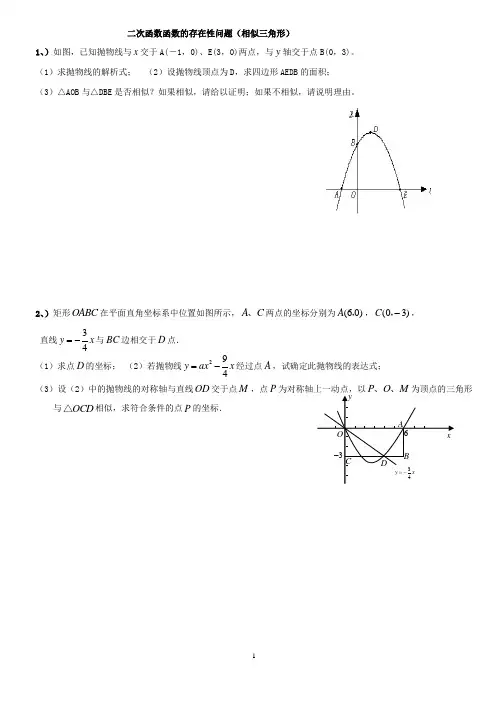
二次函数函数的存在性问题（相似三角形）1、）如图，已知抛物线与x 交于A(－1，0)、E(3，0)两点，与y 轴交于点B(0，3)。

（1）求抛物线的解析式； （2）设抛物线顶点为D ，求四边形AEDB 的面积； （3）△AOB 与△DBE 是否相似？如果相似，请给以证明；如果不相似，请说明理由。

2、）矩形OABC 在平面直角坐标系中位置如图所示，A C 、两点的坐标分别为(60)A ，，(03)C -，， 直线34y x =-与BC 边相交于D 点． （1）求点D 的坐标； （2）若抛物线294y ax x =-经过点A ，试确定此抛物线的表达式； （3）设（2）中的抛物线的对称轴与直线OD 交于点M ，点P 为对称轴上一动点，以P O M 、、为顶点的三角形与OCD △相似，求符合条件的点P 的坐标．3、）如图，已知抛物线y ＝34x 2＋bx ＋c 与坐标轴交于A 、B 、C 三点， A 点的坐标为（－1，0）过点C 的直线y ＝34tx －3与x 轴交于点Q ，点P 是线段BC 上的一个动点，过P 作PH⊥OB 于点H ．若PB ＝5t ， 且0＜t ＜1．（1）填空：点C 的坐标是_ _，b ＝ _，c ＝_ _；（2）求线段QH 的长（用含t 的式子表示）；（3）依点P 的变化，是否存在t 的值，使以P 、H 、Q 为顶点的三角形与△COQ 相似？若存在，求出所有t 的值；若不存在，说明理由．4、）已知，如图1，过点()01E -，作平行于x 轴的直线l ，抛物线214y x =上的两点A B 、的横坐标分别为-1和4，直线AB 交y 轴于点F ，过点A B 、分别作直线l 的垂线，垂足分别为点C 、D ，连接CF DF 、． （1）求点A B F 、、的坐标； （2）求证：CF DF ⊥； （3）点P 是抛物线214y x =对称轴右侧图象上的一动点，过点P 作PQ PO ⊥交x 轴于点Q ，是否存在点P 使得OPQ △与CDF △相似？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．5、如图，抛物线经过(40)(10)(02)A B C -，，，，，三点．（1）求出抛物线的解析式；（2）P 是抛物线上一动点，过P 作PM x ⊥轴，垂足为M ，是否存在P 点，使得以A ，P ，M 为顶点的三角形与OAC △相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由； （3）在直线AC 上方的抛物线上有一点D ，使得DCA △的面积最大，求出点D 的坐标．6、）如图，ABCD 在平面直角坐标系中，6AD =，若OA 、OB 的长是关于x 的一元二次方程27120x x -+=的两个根，且OA OB >．（1）求sin ABC ∠的值． （2）若E 为x 轴上的点，且163AOE S =△，求经过D 、E 两点的直线的解析式，并判断AOE △与DAO △是否相似？（3）若点M 在平面直角坐标系内，则在直线AB 上是否存在点F ，使以A 、C 、F 、M 为顶点的四边形为菱形？若存在，请直接写出F 点的坐标；若不存在，请说明理由．答案1、（09贵州安顺）解：（1） ∵抛物线与y 轴交于点（0，3），∴设抛物线解析式为)0(32≠++=a bx ax y (1′) 根据题意，得⎩⎨⎧=++=+-033903b a b a ，解得⎩⎨⎧=-=21b a∴抛物线的解析式为322++-=x x y (5′) (2)由顶点坐标公式得顶点坐标为（1，4） 设对称轴与x 轴的交点为F∴四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯=9（3）相似如图，==∴====∴2220BD BE +=, 220DE = 即： 222BD BE DE +=,所以BDE ∆是直角三角形 ∴90AOB DBE ∠=∠=︒,且AO BO BD BE ==∴AOB ∆∽DBE ∆ 2、（09青海）解：（1）点D 的坐标为(43)-，．（2）抛物线的表达式为23984y x x =-． （3）抛物线的对称轴与x 轴的交点1P 符合条件． ∵OA CB ∥， ∴1POM CDO ∠=∠． ∵190OPM DCO ∠=∠=°， ∴1Rt Rt POM CDO △∽△． ∵抛物线的对称轴3x =， ∴点1P 的坐标为1(30)P ，． 过点O 作OD 的垂线交抛物线的对称轴于点2P ． ∵对称轴平行于y 轴， ∴2P MO DOC ∠=∠．∵290POM DCO ∠=∠=°， ∴21Rt Rt P M O DOC △∽△∴点2P 也符合条件，2OP M ODC ∠=∠． ∴121390PO CO P PO DCO ==∠=∠=，°， ∴21Rt Rt P PO DCO △≌△． ∴124PP CD ==．∵点2P 在第一象限，∴点2P 的坐标为2P (34)，， ∴符合条件的点P 有两个，分别是1(30)P ，，2P (34)，3、（09广西钦州） 解：（1）（0，－3），b ＝－94，c ＝－3． （2）由（1），得y ＝34x 2－94x －3，它与x 轴交于A ，B 两点，得B （4，0）． ∴OB ＝4，又∵OC ＝3，∴BC ＝5． 由题意，得△B HP ∽△BOC ，∵OC ∶OB ∶BC ＝3∶4∶5 ， ∴HP ∶HB ∶BP ＝3∶4∶5 ， ∵PB ＝5t ，∴HB ＝4t ，HP ＝3t ． ∴OH ＝OB －HB ＝4－4t ． 由y ＝34tx －3与x 轴交于点Q ，得Q （4t ，0）． ∴OQ ＝4t ． ①当H 在Q 、B 之间时， QH ＝OH －OQ ＝（4－4t ）－4t ＝4－8t ． ②当H 在O 、Q 之间时，QH ＝OQ －OH ＝4t －（4－4t ）＝8t －4． 综合①，②得QH ＝｜4－8t ｜；（3）存在t 的值，使以P 、H 、Q 为顶点的三角形与△COQ 相似． ①当H 在Q 、B 之间时，QH ＝4－8t ， 若△QHP ∽△COQ ，则QH ∶CO ＝HP ∶OQ ，得483t -＝34tt， ∴t ＝732． 若△PHQ ∽△COQ ，则PH ∶CO ＝HQ ∶OQ ，得33t ＝484t t -，即t 2＋2t －1＝0．∴t 11，t 21（舍去）．②当H 在O 、Q 之间时，QH ＝8t －4．若△QHP ∽△COQ ，则QH ∶CO ＝HP ∶OQ ， 得843t -＝34t t ，∴t ＝2532．若△PHQ ∽△COQ ，则PH ∶CO ＝HQ ∶OQ ， 得33t ＝844t t -，即t 2－2t ＋1＝0．∴t 1＝t 2＝1（舍去）．综上所述，存在t 的值，t 11，t 2＝732，t 3＝2532．4、（09福建莆田）（1）解:方法一，如图1，当1x =-时,14y =；当4x =时,4y = ∴1A ⎛⎫- ⎪⎝⎭1，4 ()44B ， 设直线AB 的解析式为y kx b =+则1444k b k b ⎧-+=⎪⎨⎪+=⎩ 解得341k b ⎧=⎪⎨⎪=⎩∴直线AB 的解析式为314y x =+ ，当0x =时,1y = ()01F ∴， 方法二:求A B 、两点坐标同方法一,如图2,作FG BD ⊥,AH BD ⊥,垂足分别为G 、H ,交y 轴于点N ,则四边形FOMG 和四边形NOMH 均为矩形,设FO x =图3BGF BHA △∽△ BG FG BH AH ∴= 441544x -∴=-解得1x = ()0F ∴，1(2)证明：方法一：在Rt CEF △中，1,2CE EF == 22222125CF CE EF ∴=+=+=CF ∴在Rt DEF △中，42DE EF ==， 222224220DF DE EF ∴=+=+= DF ∴=由（1）得()()1141C D ---，，，， 5CD ∴=， 22525CD ∴== 222CF DF CD ∴+=90CFD ∴∠=° ∴CF DF ⊥方法二：由 （1）知5544AF AC ===，AF AC ∴= 同理：BF BD = ACF AFC ∴∠=∠AC EF ∥ ACF CFO ∴∠=∠ AFC CFO ∴∠=∠ 同理：BFD OFD ∠=∠ 90CFD OFC OFD ∴∠=∠+∠=° 即CF DF ⊥（3）存在. 如图3，作PM x ⊥轴，垂足为点M 又PQ OP ⊥ Rt Rt OPM OQP ∴△∽△ PM OMPQ OP∴= PQ PM OP OM ∴= 设()2104P x x x ⎛⎫> ⎪⎝⎭，，则214PM x OM x ==，①当RtRt QPO CFD △∽△时，12PQ CF OP DF === 21142xPM OM x ∴== 解得2x = ()121P ∴， ②当Rt Rt OPQ CFD △∽△时，2PQ DF OP CF === 2142xPM OM x ∴==解得8x = ()2816P ∴， 综上，存在点()121P ，、()2816P ，使得OPQ △与CDF △相似.（图2）5、（09山东临沂）解：（1）该抛物线过点(02)C -，，∴可设该抛物线的解析式为22y ax bx =+-．将(40)A ，，(10)B ，代入，得1642020a b a b .+-=⎧⎨+-=⎩，解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩，∴此抛物线的解析式为215222y x x =-+-．（2）存在．如图，设P 点的横坐标为m ， 则P 点的纵坐标为215222m m -+-， 当14m <<时， 4AM m =-，215222PM m m =-+-． 又90COA PMA ∠=∠=°， ∴①当21AM AO PM OC ==时， APM ACO △∽△， 即21542222m m m ⎛⎫-=-+- ⎪⎝⎭． 解得1224m m ==，（舍去），(21)P ∴，．②当12AM OC PM OA ==时，APM CAO △∽△，即2152(4)222m m m -=-+-． 解得14m =，25m =（均不合题意，舍去） ∴当14m <<时，(21)P ，． 类似地可求出当4m >时，(52)P -，． 当1m <时，(314)P --，． 综上所述，符合条件的点P 为(21)，或(52)-，或(314)--，． （3）如图，设D 点的横坐标为(04)t t <<，则D 点的纵坐标为215222t t -+-． 过D 作y 轴的平行线交AC 于E ． 由题意可求得直线AC 的解析式为122y x =-．E ∴点的坐标为122t t ⎛⎫- ⎪⎝⎭，． 2215112222222DE t t t t t ⎛⎫∴=-+---=-+ ⎪⎝⎭．22211244(2)422DAC S t t t t t ⎛⎫∴=⨯-+⨯=-+=--+ ⎪⎝⎭△．∴当2t =时，DAC △面积最大．(21)D ∴，． 6、（09牡丹江）（1）解27120x x -+=得1243x x ==，，OA OB >， 43OA OB ∴==，在Rt AOB △中，由勾股定理有5AB = 4sin 5OA ABC AB ∴∠== （2）∵点E 在x 轴上，163AOES =△ 11623AO OE ∴⨯= 83OE ∴= 880033E E ⎛⎫⎛⎫∴- ⎪ ⎪⎝⎭⎝⎭，或， 由已知可知D （6，4） 设DE y kx b =+，当803E ⎛⎫⎪⎝⎭，时有46803k b k b =+⎧⎪⎨=+⎪⎩解得65165k b ⎧=⎪⎪⎨⎪=-⎪⎩∴61655DEy x =- 同理803E ⎛⎫- ⎪⎝⎭，时，6161313DE y x =+ 在AOE △中，89043AOE OA OE ∠===°，， 在AOD △中，9046OAD OA OD ∠===°，， OE OAOA OD= AOE DAO ∴△∽△ （3）满足条件的点有四个123475224244(38)(30)1472525F F F F ⎛⎫⎛⎫----- ⎪ ⎪⎝⎭⎝⎭，；，；，；，。

专题二 相似三角形的存在性问题解相似三角形的存在问题，一般分为三个步骤：第一步寻找分类标准，第二步列方程，第三步解方程并验根.难点在于寻找分类标准，寻找恰当的分类标准，可以使得解的个数不重复不遗漏，也可以使得列方程和解方程又好又快.一般情况下，寻找一组相等的角，然后根据对应边成比例，分成两种情况列方程.1.如图，抛物线213482y x x =-+与x 轴交于A 、B 两点（A 点在B 点左侧），与y 轴交于点C.动直线EF （EF//x 轴）从点C 出发，以每秒1个单位长度的速度沿y 轴负方向平移，且分别交y 轴、线段BC 于点E 、F 两点，动点P 同时从点B 出发，在线段OB 上以每秒2个单位长度的速度向原点O 运动.是否存在t 值，使得△BPF 与△ABC 相似？若存在，试求出t 的值；若不存在，请说明理由.2.如图，在平面直角坐标系xOy 中，抛物线21b 2y x x c =-++,经过点A(1,3)、B(0,1) 1.求抛物线的表达式及其顶点坐标；2.经过点A 作x 轴的平行线交抛物线于另一点C.在y 轴上取一点P ，使△ABP 与△ABC 相似，求满足条件的所有P 点坐标.3.如图，△ABC 中,AB=5，AC=3，cos ∠A=310.点D 在AB 边上（点D 不与点A 、点B 重合），作DE//BC 交AC 于点E.在BC 边上是否存在点F ，使△ABC 与三角形EF 相似？若存在，请求出线段BF 的长；若不存在，请说明理由.4.如图，抛物线23y ax bx =+-与x 轴交于点A(1,0)、B(3,0)两点，与y 轴交于点D ，顶点为C.（1）求此抛物线的解析式；（2）在x 轴下方的抛物线上是否存在点M ，过M 作MN ⊥x 轴于点N ，使以A 、N 、M 为顶点的三角形与△BCD 相似？若存在，求出点M 的坐标；若不存在，请说明理由.5.如图，抛物线2(0)y ax c a =+≠与y 轴交于点A ，与x 轴交于点B 、C 两点（点C 在x 轴正半轴上），△ABC 为等腰直角三角形，且面积为4.现将抛物线沿BA 方向平移，平移后的抛物线国电C 时，与x 轴的另一个交点为E ，其顶点为F ，对称与x 轴的交点为H.（1）求a c 、的值；（2）连接OF,试判断△OEF 是否为等腰三角形，并说明理由；（3）现将一足够大的三角板的直角顶点Q 放在射线AF 或射线HF 上，一直角边始终过点E ，另一直角边与y 轴相交于点P.是否存在这样的点Q ，使以点P 、Q 、E 为顶点的△POE 全等？若存在，求出点Q 的坐标；若不存在，请说明理由.6.在平面直角坐标系中，一个二次函数的图像经过A(1,0)、B(3,0)两点.（1）写出这个二次函数图像的对称轴；（2）设这个二次函数图像的顶点为D ，与y 轴交于点C ，它的对称轴与x 轴交于点E ，连接AC 、DE 和DB.当△AOC 与△DEB 相似时，求这个二次函数的解析式.7.如图，点O 为据新华社ABCD 的对称中心，AB=10cm ，BC=12cm.点E 、F 、G 分别从A 、B 、C 三点同时出发，沿矩形的边按逆时针方向匀速运动.点E 的运动速度为每秒1cm ，点F的运动速度为3cm 每秒，点G 的运动速度为每秒1.5cm.当点F 到达C 时，三个点随之停止运动.在运动过程中，△EBF 关于直线EF 的对称图形是△EB 'F.设点E 、F 、G 运动时间为t 秒.（1）当t= 秒时，四边形'EBFB 为正方形；（2）若以点E 、B 、F 为顶点的三角形与以点F 、C 、G 为顶点的三角形相似，求t 值.（3）是否存在实数t ，使得点'B 与点O 重合？若存在，求出t 值；若不存在，请说明理由.8.如图，二次函数2(0)y ax bx a =+≠的图像经过点A(1,4)，对称轴是直线x=-32，线段AD 平行于x 轴，交抛物线雨点D.在y 轴上取一点C （0,2），直线AC 交抛物线与点B ，连接OA 、OB 、OD 、BD.（1）求该二次函数的解析式；（2）求点B 的坐标和坐标平面内使△EOD △AOB 得点E 的坐标；（3）设点F 是BD 的中点，点P 是线段DO 上的动点，为PD 为何值时，将△BPF 沿边PF 翻折，是△BPE 与△DPF 重叠部分的面积是△BDP 面积的14. 9.如图，在平面直角坐标系中，直线L1过点A （1,0）且与y 轴平行，直线L2过点B （0,2）且与x 轴平行，直线L1与L2相交于点P.点E 为直线L2上一点，反比例函数(0)k y k x =>的图像过点E 且与直线L1相交于点F.（1）若点E 与点P 重合，求k 值；（2）连接OE 、OF 、EF ，若k>2，且△OEF 的面积为△PEF 的面积的2倍，去点E 的坐标；（3）是否存在点E 及y 轴上的点M ，使得以M 、E 、F 为顶点的三角形与△PEF 全等？若存在，求出点E 的坐标；若不存在，请说明理由.10.如图，在△ABC 中，AB=AC=BC=8.⊙A 的半径为2，动点P 从点B 出发沿BC 方向以每秒1个单位长度的速度向点C 运动，以点P 为圆心，以PB 为半径作⊙P ，设点P 的运动的时间为t.（1）当⊙P 与直线AC 相切时，求t 值；（2）当⊙P 与⊙A 相切时，求t 值；（3）延长BA 交⊙A 于点D ，连接AP 交⊙A 于点E ，连接DE 并延长交BC 于点F.当△ABP 与△FBD 相似时，求t 值.11.如图，在平面直角坐标系中，A 点坐标为（8,0），B 点坐标为（0,6），点C 是x 轴上的一点，沿直线BC 翻折，点O 正好落在AB 边上的点D 处.（1）去点C 的坐标；（2）设直线CD 与y 轴交于点E ，求点E 的坐标；（3）点P 在直线AB 上，直线CP 与y 轴交于点F ，如果△ACP 与△BPF 相似，求直线CP 的解析式.。

相似三角形的存在性问题解题策略专题攻略相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验，如例题1、2、3、4．应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等，如例题6．应用判定定理3解题不多见，如例题5，根据三边对应成比例列连比式解方程（组）． 例题解析例1、 如图1-1，抛物线213482y x x =-+与x 轴交于A 、B 两点（A 点在B 点左侧），与y 轴交于点C ．动直线EF （EF //x 轴）从点C 开始，以每秒1个单位的速度沿y 轴负方向平移，且分别交y 轴、线段BC 于E 、F 两点，动点P 同时从点B 出发，在线段OB 上以每秒2个单位的速度向原点O 运动．是否存在t ，使得△BPF 与△ABC 相似．若存在，试求出t 的值；若不存在，请说明理由．图1-1【解析】△BPF 与△ABC 有公共角∠B ，那么我们梳理两个三角形中夹∠B 的两条边．△ABC 是确定的．由213482y x x =-+，可得A (4, 0)、B (8, 0)、C (0, 4)．于是得到BA ＝4，BC ＝12CE CO EF OB ==． △BPF 中，BP ＝2t ，那么BF 的长用含t 的式子表示出来，问题就解决了．在Rt △EFC 中，CE ＝t ，EF ＝2t ，所以CF ．因此)BF t ==-．于是根据两边对应成比例，分两种情况列方程： ①当BA BPBC BF ==43t =（如图1-2）．②当BA BFBC BP ==207t =（如图1-3）．图1-2 图1-3 例2、 如图2-1，在平面直角坐标系中，顶点为M 的抛物线y ＝ax 2＋bx （a ＞0）经过点A 和x 轴正半轴上的点B ，AO ＝BO ＝2，∠AOB ＝120°．（1）求这条抛物线的解析式；（2）连结O M ，求∠AOM 的大小；（3）如果点C 在x 轴上，且△ABC 与△AOM 相似，求点C 的坐标．图2-1【解析】△ABC 与△AOM 中相等的一组角在哪里呢？本题由简到难，层层深入．第（1）题求出抛物线的解析式，得到顶点M 的坐标，为第（2）题求∠AOM 的大小作铺垫；求得了∠AOM 的大小，第（3）题暗示了要在△ABC 中寻找与∠AOM 相等的角．（1）如图2-2，过点A 作AH ⊥y 轴，垂足为H ．容易得到A (1-．再由A (1-、B (2,0)两点，可求得抛物线的解析式为2y x x =．（2）由221)y x x ==-，得顶点M (1,．所以tan BOM ∠=．所以∠BOM ＝30°．所以∠AOM ＝150°．图2-2（3）由A (1-、B (2,0)，可得∠ABO ＝30°．因此当点C 在点B 右侧时，∠ABC ＝∠AOM ＝150°．所以△ABC 与△AOM 相似，存在两种情况：①当BA OABC OM ==时，2BC ==．此时C (4,0)（如图2-3）．②当BC OA BA OM ==时，6BC ==．此时C (8,0)（如图2-4）．图2-3 图2-4例3、 如图3-1，抛物线y ＝ax 2＋bx －3与x 轴交于A (1, 0)、B (3, 0)两点，与y 轴交于点D ，顶点为C ．（1）求此抛物线的解析式；（2）在x 轴下方的抛物线上是否存在点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，求出点M 的坐标；若不存在，请说明理由．图3-1【解析】△AMN 是直角三角形，因此必须先证明△BCD 是直角三角形．一般情况下，根据直角边对应成比例分两种情况列方程．（1）抛物线的解析式为y ＝－x 2＋4x －3．（2）由y ＝－x 2＋4x －3＝－(x －2)2＋1，得D (0,－3)，C (2, 1)．如图3-2，由B (3, 0)、D (0,－3)、C (2, 1)，可知∠CBO ＝45°，∠DBO ＝45°．所以∠CBD ＝90°，且13BC BD ==．图3-2 图3-3 图3-4设点M 、N 的横坐标为x ，那么NM ＝－y M ，而NA 的长要分N 在A 的右边或左边两种情况，因此列方程要“两次分类”：当N 在A 右侧时，NA ＝x －1，分两种情况列方程： ①当3NA BD NM BC ==时，13(1)(3)x x x -=--．解得103x =．此时M 107(,)39-（如图3-3）． ②当13NA BC NM BD ==时，11(1)(3)3x x x -=--．解得x ＝6．此时M (6,－15)（如图3-5）． 当N 在A 左侧时，NA ＝1－x ，也要分两种情况列方程： ①当3NA BD NM BC ==时，13(1)(3)x x x -=--．解得83x =＞1，不符合题意（如图3-4）． ②当13NA BC NM BD ==时，11(1)(3)3x x x -=--．解得x ＝0，此时M (0,－3)（如图3-6）．图3-5 图3-6例4、 如图4-1，在平面直角坐标系中，A (8,0)，B (0,6)，点C 在x 轴上，BC 平分∠OBA ．点P 在直线AB 上，直线CP 与y 轴交于点F ，如果△ACP 与△BPF 相似，求直线CP 的解析式．图4-1【解析】首先求得点C (3,0)．△ACP 与△BPF 中，相等的角在哪里啊？①如图4-2，当点P 在线段AB 上时，△ACP 与△BPF 中，∠APC 与∠BPF 是邻补角，如果这两个邻补角一个是锐角，一个是钝角，两个三角形怎么可能相似呢？因此CP 与AB 是垂直的．可以求得F (0,－4)，于是直线CF (CP )为443y x =-． ②如图4-3，当点P 在AB 的延长线上时，△ACP 与△BPF 有公共角∠P ．于是∠OFC ＝∠PFB ＝∠A ，可以求得F (0, 4)，因此直线CF (CP )为443y x =-+． ③如图4-4，当点P 在BA 的延长线上时，∠B 与∠PCA 不可能相等．在△AOB 中，根据大边对大角，∠B ＞∠BAO ；∠BAO 又是△PCA 的一个外角，∠BAO ＞∠PCA ．图4-2 图4-3 图4-4例5、 如图5-1，二次函数y ＝x 2＋3x 的图象经过点A (1,a )，线段AD 平行于x 轴，交抛物线于点D ．在y 轴上取一点C (0, 2)，直线AC 交抛物线于点B ，连结OA 、OB 、OD 、BD ．求坐标平面内使△EOD ∽△AOB 的点E 的坐标；图5-1【解法一】点A 、D 、B 都是确定的，可以求得A (1, 4)，D (－4, 4)，B (－2,－2)．所以AO =，BO =，AB =DO =△EOD ∽△AOB ，对应边已经确定，因此我们可以根据判定定理3列方程． 由EO OD DE AO OB BA ===EO =DE = 设点E 的坐标为(x , y )，根据EO 2＝68，DE 2＝180，列方程组222268,(4)(4)180.x y x y ⎧+=⎪⎨++-=⎪⎩解得118,2,x y =⎧⎨=-⎩ 222,8,x y =⎧⎨=-⎩ 所以点E 的坐标为(8,－2)或(－2, 8)．上面的解题过程是“盲解”，我们并不明白两个三角形的位置关系．【解法二】如图5-2，△AOB 是确定的，△AOB 与△EOD 有公共点O ，OB ∶OD ＝1∶2，∠BOD ＝90°．如果△EOD ∽△AOB ，我们可以把△AOB 绕着点O 顺时针旋转，使得点B ′落在OD 上，此时旋转角为90°，点B ′恰好落在OD 的中点．按照这个运动规则，点A (1, 4) 绕着点O 顺时针旋转90°，得到点A ′(4,－1)，点A ′是线段OE 的中点，因此点E 的坐标为(8,－2)．如图5-3，点E (8,－2)关于直线OD （即直线y ＝－x ）对称的点为E ′(2,－8)．图5-2 图5-3例6、 如图6-1，在△ABC 中，AB ＝AC ＝BC ＝8．⊙A 的半径为2，动点P 从点B 出发沿BC 方向以每秒1个单位的速度向点C 运动．延长BA 交⊙A 于点D ，连结AP 交⊙A 于点E ，连结DE 并延长交BC 于点F ．设点P 运动的时间为t 秒，当△ABP 与△FBD 相似时，求t 的值．图6-1【解析】△ABC 是等腰直角三角形，⊙A 是确定的，先按照题意把图形补充完整． 如图6-2，容易发现△ABP 与△FBD 有公共角∠B ，如果根据对应边成比例列方程BA BDBP BF =或BA BF BP BD=，其中BA ＝BP ＝t ，BD ＝2，但是用含t 的式子表示BF 困难重重啊！图6-2 图6-3 图6-4我们另起炉灶，按照判定定理1来解决．△ABP 与△FBD 有公共角∠B ，我们以∠D 为分类标准，分两种情况讨论它们相似： 第一种情况，如图6-3，∠BAP ＝∠D 是不可能的，这是因为∠BAP 是等腰三角形ADE 的外角，∠BAP ＝2∠D ．第二种情况，如图6-4，当∠BP A ＝∠D 时，在△ABP 中，由于∠BAP ＝2∠D ＝2∠BP A ， 因此45°＋3∠BP A ＝180°．解得∠BP A ＝45°．此时△ABP 是等腰直角三角形，P 与C 重合，所以t ＝8．解答这道题目，如果选取点P 的3个不同位置，按照题意画图，可以帮助我们探究．在讨论第二种情况∠BP A ＝∠D 时，我们容易被已知图6-1给定的点P 的位置所误导，以为图6-2中“锐角∠D ”与“钝角∠BP A ”不可能相等．。

培优讲义——相似三角形的存在性问题
常见方法一：先寻找一组等角，再分两种情况讨论另外两组对应角相等；
常见方法二：寻找一组等角，分两种情况列比例方程，解方程并检验。

1、如图，在直角坐标系中，已知点(2,0)A ，(0,4)B ，(1,0)C ，在坐标轴上找到点
D ，使△AOB 与△DOC 相似，求出D 点的坐标，并说明理由．
2、如下图，在矩形ABCD 中，AB=12 cm ，BC=6 cm ．点P 沿AB 边从点A 开始向点B 以2 cm/s 的速度移动；点Q 沿DA 边从点D 开始向点A 以1 cm/s 的速度移动．如果P 、Q 同时出发，用t （s ）表示移动的时间（0≤t≤6）那么：
（1）当t 为何值时，△QAP 为等腰直角三角形？
（2）求四边形QAPC 的面积，提出一个与计算结果有关的结论；
（3）当t 为何值时，以点Q 、A 、P 为顶点的三角形与△ABC 相似？
3、如图，在平面直角坐标系中，A (8,0)，B (0,6)，点C 在x 轴上，BC 平分∠OBA ．点P 在
直线AB 上，直线CP 与y 轴交于点F ，如果△ACP 与△BPF 相似，求直线CP 的解析式．
26、（13分）如图，正方形ABCD 边长为10cm ，P 是BC 上的任意一点（不含端点B 、C ），连结AP ，过点P 作PE ⊥PA 交CD 于点E ．（1）求证：△ABP ∽△PCE ；
（2）当P 在BC 上运动时，对应的点E 也随之在CD 上运动，设CP x =，DE y =，求y 与x 的函数关系式及y 的取值范围。

（3）在线段BC 上，是否存在不同于P 的点Q ，使得QA ⊥QE ？若存在，求线段BQ 与BP 之间的数量关系；若不存在，请说明理由。

（备用图）。