最新13.1算术平方根教案优质课

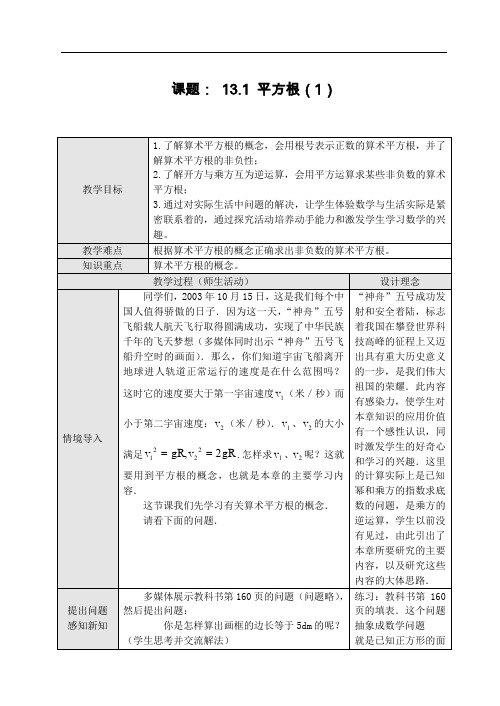
13.1 平方根（1）大连世纪中学关丽娜一、内容和内容解析1．内容算术平方根的概念和求法．2．内容解析《平方根》是人教版八年级上第十三章实数第一节内容，隶属于“数与代数”领域。

本章的主要内容是平方根、立方根的概念和求法，实数的有关概念和运算.通过本章的学习，学生对数的认识就由有理数扩大到实数范围.本章虽内容不多，篇幅不大，但在中学数学中占有重要的地位，本章的内容不仅是后面学习二次根式、一元二次方程以及解三角形等知识的基础，也为学习高中数学中的不等式、函数以及解析几何的大部分知识做好准备。

本节重点结合实际问题情景认识算术平方根、平方根的意义，能够对算术平方根进行符号表示，能够利用概念的本质探获求算术平方根、平方根的方法，理解算术平方根、平方根的性质。

本节共三课时，本课为第一课时，从学生熟悉的正方形面积与边长之间的关系入手将问题1概括为“已知一个数的平方，求这个数”的新问题，从而给出算术平方根的概念，并对概念进行辨析理解、巩固和运用，通过探究活动，利用数形结合的思想直观感受2的大小，通过对实际生活中问题的解决，让学生体验新概念的产生是实际生活和科技发展的需要。

通过对这一节课的学习，既可以让学生了解算术平方根的概念，会用符号表示正数的算术平方根，并了解算术平方根的非负性，又可以渗透化归思想（将求算术平方根的运算转化为求幂底数的运算）将为学生以后学习平方根奠定基础；同时这一节也是联系数学与生活的桥梁。

基于以上分析，可以确定本课的教学重点是：弄清算术平方根的概念，初步感受无理数.二、目标和目标解析1．目标（1）了解算术平方根的概念，并了解算术平方根的双重非负性；（2）会用符号表示任意非负数的算术平方根，建立初步的数感和符号感（3）通过几个类似问题，能抽象出数学问题，发展抽象思维．2．目标解析达成目标（1）的标志是：会用平方运算求某些非负数的算术平方根，并能对概念进行准确的辨析．达成目标（2）的标志是学生会求用文字和符号两种语言描述的算术平方根，并会用符号表示。

13.1平方根（第一课时）
◆随堂检测
1、一般地，如果一个正数的平方等于a ，即x 2=a ，那么这个正数x 叫做a 的 记作 读作 ，a 叫做
2、用计算器计算5（精确到0.0001）
3、41
的算术平方根是
4、若一个数的算术平方根等于它本身，这个数是
5、下列数没有算术平方根的是（ ）
A.0
B.-1
C.10
D.102
6、探究20的大小
◆课下作业
1、如果2a-18=0，那么a 的算术平方根是 .
2、0.0625的算术平方根是 ，256的算术平方根是 .
31=的根是 ．
4、比较大小 ：15 和 4， 21
5- 和 0.5
5、填空找规律（结果精确到0.0001）
（1）利用计算器分别求
50050 5 5.0====
（2）由（1）的结果，你能发现什么规律呢?
6、一个正方形的面积是24平方厘米，求这个正方形的周长大约是多少？（精确到0.01）
7、计算下列各数的算术平方根
（1）144 （2）810 （3）26 （4）225121
●体验中考
1、3最接近的整数是（ ）
A ．0
B ．2
C ．4
D ．5
2、 4的算术平方根是（ ）
A ．2±
B ．2
C ． D
3x 的取值范围是（ ）
A ．x ≥0
B ．0x <
C ．0x ≠
D ．0x >。

《13.1算术平方根》教案一、 教学目标1、 知识目标 了解算术平方根的概念，会求一个非负数的算术平方根；会用计算器求一个非负数的算术平方根（算术平方根的近似值）2、 能力目标：通过实例培养学生的动手能力3、 情感目标：通过对问题的解决，让学生认识到数学与生活是密切联系的，培养学生对数学的兴趣。

二、教学方法1、 启发探究2、直观演示三、教学重难点重点：算术平方根的概念及求法难点：正确理解算术平方根的概念四、教学过程（一）复习旧知：1、 什么是一个数的平方根？如何表示？2、 求下列各数的平方根(3) (-2005)2（二）新知讲解1、算术平方根的定义：一个正数 a 有两个平方根 ±a ，其中它的正的平方根a 叫做它的算术平方根同。

即：一个正数正的平方根叫做这个数的算术平方根。

特殊的：0的算术平方根是0.2、 例1 求下列各数的算术平方根（1）100 （2） （3）0.0001练习：求下列各数的算术平方根（1）121 （2）（－3）2 （3）0.000025判断：（1）5是25的算术平方根；( )（2）-6是 36 的算术平方根； ( )（3）0的算术平方根是0； ( )（4）0.01是0.1的算术平方根 ( )（5）-5是-25的算术平方根。

( )3、例2：求下列各数的平方根和算术平方根（1）241 （2）（－25）2 （3）81 练习：求下列各数的平方根和算术平方根（1） （2） （3）4、例3计算练习（1）16的算术平方根是（2）16的算术平方根是（3）36的算术平方根是（4）()23-的算术平方根5、探究：等于多少？呢？f怎样用两个面积为1的小正方形拼成一个面积为2的大正方形？你知道这个大正方形的边长是多少吗？设大正方形的边长为x，则 x2 =2.由算术平方根定义：则x=2你知道2有多大吗?(用逼近法)6、计算器的使用：1）计算器求下列各数的算术平方根（算术平方根的近似值）2）利用计算器计算，并将结果填表中，你发现了什么规律（三）、课堂小结算术平方根：一个正数的正的平方根叫作这个算术平方根。

13.1平方根（第3课时）一、教学目标1.经历平方根概念的形成过程，了解平方根的概念，会求某些正数（完全平方数）的平方根.2.经历有关平方根结论的归纳过程，知道正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根.二、重点和难点1.重点：平方根的概念.2.难点：归纳有关平方根的结论.三、合作探究（一）基本训练，巩固旧知1.填空：如果一个的平方等于a，那么这个叫做a的算术平方根，a的算术平方根记作 .2.填空：(1)面积为16的正方形，边长＝＝；(2)面积为15的正方形，边长＝≈（利用计算器求值，精确到0.01）.3.填空：(1)因为1.72＝2.89，所以2.89的算术平方根等于，即 2.89＝；(2)因为1.732＝2.9929，所以3的算术平方根约等于，即3≈ .（二）什么是平方根呢？大家先来思考这么一个问题.（三）如果一个正数的平方等于9，这个正数是多少？如果一个数的平方等于9，这个数是多少？和算术平方根的概念类似，（指准32＝9）我们把3叫做9的平方根，（指准(-3)2＝9）把－3也叫做9的平方根，也就是3和－3是9的平方根（板书：3和－3是9的平方根）.我们再来看几个例子.x2 16 36 49 1 4 25x同学们大概已经明白了平方根的意思.平方根的概念与算术平方根的概念是类似的，谁会用一句话概括什么是平方根？平方根：如果一个数的平方等于a，那么这个数叫做a的平方根.大家把平方根概念默读两遍.（生默读）平方根概念与算术平方根概念只有一点点区别，哪一点点区别？四、精讲精练例1、求下面各数的平方根：(1)100； (2)0.25； (3)0； (4)－4；(1)因为（±10）2＝100），所以100的平方根是＋10和－100的平方是0，正数的平方是正数，负数的平方还是正数，所以任何数的平方都不会等于－4.这说明什么？从这个例题你能得出什么结论？（稍停片刻）正数有几个平方根？0有几个平方根？负数有几个平方根？小组讨论：正数有平方根（板书：正数有两个平方根）.平方根有什么关系？0的平方根有个，平方根是 .负数平方根大家把平方根的这三条结论读两遍.精练1.填空：(1)因为（）2＝49，所以49的平方根是；(2)因为（）2＝0，所以0的平方根是；(3)因为（）2＝1.96，所以1.96的平方根是；2.填空：(1)121的平方根是，121的算术平方根是；(2)0.36的平方根是，0.36的算术平方根是；(3) 的平方根是8和－8，的算术平方根是8；(4) 的平方根是35和35，的算术平方根是35.3.判断题：对的画“√”，错的画“×”.(1)0的平方根是0 （）(2)－25的平方根是－5；（）(3)－5的平方是25；（）(4)5是25的一个平方根；（）(5)25的平方根是5；（）(6)25的算术平方根是5；（）(7)52的平方根是±5；（）(8)(-5)2的算术平方根是－5. （）五、课堂小结：如果一个数的平方等于a，那么这个数叫做a的平方根.六、作业P75 3 p76 8。

人教版数学八年级上册13.1《算术平方根》教学设计一. 教材分析《算术平方根》是人教版数学八年级上册第13.1节的内容，本节课的主要目的是让学生理解算术平方根的概念，掌握求算术平方根的方法，并能应用其解决实际问题。

教材通过引入平方根的概念，引导学生探究算术平方根的性质，从而掌握求算术平方根的方法。

二. 学情分析学生在七年级时已经学习了平方根的概念，他们对平方根有一定的了解。

但是，对于算术平方根的概念和性质，他们可能还比较陌生。

因此，在教学过程中，需要引导学生通过实际操作和思考，来理解和掌握算术平方根的概念和性质。

三. 教学目标1.理解算术平方根的概念，掌握求算术平方根的方法。

2.能够应用算术平方根的概念解决实际问题。

3.培养学生的逻辑思维能力和运算能力。

四. 教学重难点1.算术平方根的概念和性质。

2.求算术平方根的方法。

五. 教学方法1.情境教学法：通过引入实际问题，引导学生理解和应用算术平方根的概念。

2.探究教学法：引导学生通过实际操作和思考，探究算术平方根的性质。

3.讲解教学法：对算术平方根的概念和性质进行讲解，帮助学生理解和掌握。

六. 教学准备1.教学课件：制作课件，展示算术平方根的概念和性质。

2.练习题：准备一些练习题，用于巩固学生的学习成果。

七. 教学过程1.导入（5分钟）利用课件展示一些实际问题，如面积、体积等，引导学生思考如何求解这些问题。

通过引导学生回顾平方根的概念，从而引出算术平方根的概念。

2.呈现（10分钟）利用课件呈现算术平方根的定义和性质，引导学生理解和掌握。

同时，给出一些例子，让学生了解如何求解算术平方根。

3.操练（10分钟）让学生分组讨论，尝试解决一些求算术平方根的实际问题。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）让学生独立完成一些练习题，检验他们对算术平方根的理解和掌握程度。

教师选取部分学生的作业进行讲解和分析。

5.拓展（10分钟）引导学生思考：如何求解一个数的算术平方根？让学生通过实际操作和思考，探究求解算术平方根的方法。

13.1平方根（三）教学目标：1、掌握平方根的概念.2 、掌握开平方的概念3、能够通过平方运算求一个非负数的平方根.教学重点：平方根的概念.教学难点：求一个非负数的平方根.教学过程：一， 知识回顾：什么叫算术平方根？一般地，如果一个正数x 的平方等于a ，即 ，那么这个正数x 叫做a 的算术平方根.规定：0的算术平方根是0二， 探索新知什么是平方根呢？大家先来思考这个问题：如果一个数的平方等于9，这个数多少？因为 ，所以这个数可以是3由于 ，所以这个数也可以是-3. 因此，如果一个数的平方等于9，那么这个数是3或-3.和算术平方根的概念相似，我们把3叫做9的平方根，把-3也叫做9的平方根，也就是3和-3是9的平方根。

认真观察下式可知∵ ，∴5和-5是25的平方根. ∵ ，∴4和-4是16的平方根. ∵ ，∴0的平方根是0.∵ ，∴-4没有平方根.归纳：一般地，如果一个数的平方等于 a , 那么这个数叫做 a 的平方根或二次方根.这就是说，如果 ，那么x 叫做a 的平方根. a x =2932=()932=-()2552=±()1642=±002=()4-2=无ax =2例如：（1）∵ ∴3和－3都是9的平方根,简记 是9的平方根。

（2）∵ ∴ 的平方根填表：求一个数 a 的平方根的运算，叫做开平方，开平方运算的结果就是平方根. 我们看到,3和-3的平方等于 9 , 9的平方根是 3和-3 ，所以平方与开平方互为逆运算，根据这种关系，可以求一个数的平方根.三.例题讲解例4 求下列各数的平方根：（1）100； （2） ； （3）0.25四，随堂练习五，课堂小结（1）如果一个数的平方等于a ，这个数叫做a 的平方根；（2）求一个数的平方根的运算叫做开平方，平方和开平方互为逆运算． 六,作业：P75习题13.1 第3 ,8题 ()93,9322=-=3±49973,4997322=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛49973-73都是和169。