当前位置：文档之家 › 第四章金属自由电子论

第四章金属自由电子论

  • 格式：pdf
  • 大小：1.77 MB
  • 文档页数：64

下载文档原格式

  / 64

合集下载

材料物理基础习题

材料物理基础习题

课后练习思考题：第一章晶体结构1-1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。

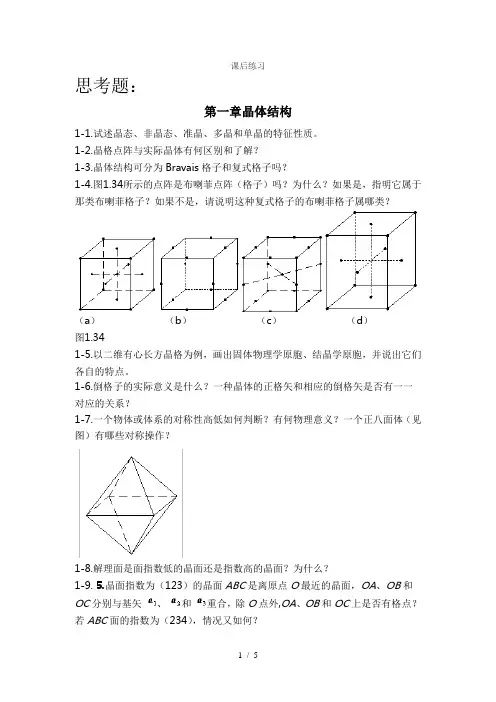
1-2.晶格点阵与实际晶体有何区别和了解？1-3.晶体结构可分为Bravais格子和复式格子吗？1-4.图1.34所示的点阵是布喇菲点阵（格子）吗？为什么？如果是，指明它属于那类布喇菲格子？如果不是，请说明这种复式格子的布喇菲格子属哪类？（a）（b）（c）（d）图1.341-5.以二维有心长方晶格为例，画出固体物理学原胞、结晶学原胞，并说出它们各自的特点。

1-6.倒格子的实际意义是什么？一种晶体的正格矢和相应的倒格矢是否有一一对应的关系？1-7.一个物体或体系的对称性高低如何判断？有何物理意义？一个正八面体（见图）有哪些对称操作？1-8.解理面是面指数低的晶面还是指数高的晶面？为什么？1-9. 5.晶面指数为（123）的晶面ABC是离原点O最近的晶面，OA、OB和OC分别与基矢、和重合，除O点外,OA、OB和OC上是否有格点？若ABC面的指数为（234），情况又如何？1-10.带轴为[001]的晶带各晶面，其面指数有何特点？1-11. 与晶列[l1l2l3]垂直的倒格面的面指数是什么?1-12. 在结晶学中,晶胞是按晶体的什么特性选取的?1-13. 六角密积属何种晶系?一个晶胞包含几个原子?1-14.体心立方元素晶体, [111]方向上的结晶学周期为多大?实际周期为多大?1-15. 面心立方元素晶体中最小的晶列周期为多大?该晶列在哪些晶面内?1-16. 在晶体衍射中，为什么不能用可见光？第二章固体的结合2-1.试述离子键、共价键、金属键、范德瓦尔斯键和氢键的基本特征.2-2.有人说“晶体的内能就是晶体的结合能”，对吗？2-3.当2个原子由相距很远而逐渐接近时，二原子间的力与势能是如何逐渐变化的？2-4.为什么金属比离子晶体、共价晶体易于进行机械加工并且导电、导热性良好？2-5.是否有与库仑力无关的晶体结合类型?2-6.如何理解库仑力是原子结合的动力?2-7.晶体的结合能,晶体的内能,原子间的相互作用势能有何区别?2-8.原子间的排斥作用取决于什么原因?2-9.原子间的排斥作用和吸引作用有何关系?起主导的范围是什么?2-10.共价结合为什么有“饱和性”和“方向性”?2-11.共价结合,两原子电子云交迭产生吸引,而原子靠近时,电子云交迭会产生巨大的排斥力,如何解释?2-12.试解释一个中性原子吸收一个电子一定要放出能量的现象.2-13.如何理解电负性可用电离能加亲和能来表征?2-14.何为杂化轨道?2-15.你认为固体的弹性强弱主要由排斥作用决定呢,还是吸引作用决定?第三章晶格振动与晶体的热学性质3-1.什么是简谐近似？3-2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线，并简要说明其意义。

(完整版)第四章金属自由电子理论

(完整版)第四章金属自由电子理论

第四章 金属自由电子理论1.金属自由电子论作了哪些假设？得到了哪些结果？解：金属自由论假设金属中的价电子在一个平均势场中彼此独立，如同理想气体中的粒子一样是“自由”的，每个电子的运动由薛定谔方程来描述；电子满足泡利不相容原理，因此，电子不服从经典统计而服从量子的费米－狄拉克统计。

根据这个理论，不仅导出了魏德曼－佛兰兹定律，而且而得出电子气对晶体比热容的贡献是很小的。

2.金属自由电子论在k 空间的等能面和费米面是何形状？费米能量与哪些因素有关？解：金属自由电子论在k 空间的等能面和费米面都是球形。

费米能量与电子密度和温度有关。

3.在低温度下电子比热容比经典理论给出的结果小得多，为什么？解：因为在低温时，大多数电子的能量远低于费米能，由于受泡利原理的限制基本上不能参与热激发，而只有在费米面附近的电子才能被激发从而对比热容有贡献。

4.驰豫时间的物理意义是什么？它与哪些因素有关？解：驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间，它的引入是用来描写晶格对电子漂移运动的阻碍能力的。

驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。

5.当2块金属接触时，为什么会产生接触电势差？解：由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同，所以这2块金属接触时，会产生接触电势差。

6.已知一维金属晶体共含有N 个电子，晶体的长度为L ，设0=T K 。

试求： （1）电子的状态密度； （2）电子的费米能级； （3）晶体电子的平均能量。

解：(1)该一维金属晶体的电子状态密度为：dEdkdk dZ dE dZ E ⋅==)(ρ …………………………（1） 考虑在k 空间中，在半径为k 和dk k +的两线段之间所含的状态数为：dk Ldk dZ π=∆=k 2 …………………………（2） 又由于 mk E 222η=所以 mkdk dE 2η= …………………………（3） 将（2）和（3）式代入（1）式，并考虑到每个状态可容纳2个自旋相反的电子，得该一维金属晶体中自由电子的状态密度为：EmL E 22)(ηπρ= (4)（2）由于电子是费米子，服从费米—狄拉克统计，即在平衡时，能量为E 的能级被电子占据的几率为：11)(+=-TK E E B F eE f (5)于是，系统中的电子总数可表示为：⎰∞=)()(dE E E f N ρ (6)由于0=T K ，所以当0F E E >，有0)(=E f ，而当0F E E ≤，有1)(=E f ，故（6）式可简化为：⎰=)(FE dE E N ρ＝⎰0022FE dE E m L ηπ＝240FmE L ηπ由此可得： 222208mL N E Fηπ= (7)（3）在0=T K 时，晶体电子的平均能量为： ⎰∞=0)()(1dEE E Ef N E ρ＝dE EmL E N FE 2210⎰⋅ηπ＝230)(232F E m N L ηπ＝022223124F E mL N =ηπ 7.限制在边长为L 的正方形中的N 个自由电子，电子的能量为)(2),(222y x y x k k mk k E +=η。

固体物理学：第4章 金属自由电子论

固体物理学：第4章 金属自由电子论


1、费米分布的性质
FFD
1
FFD
1 e / kT
1
1T 0 f FFD 1
f
FFD 0
εf ε
T 0 时所有粒子排满费米能级以下的能级，
费米能级以上能级全空。
UESTC
FFD
1
（2）T 0
f
1 FFD 2
1/2
随着温度升高，有部分粒子
获得能量从 f以下能态跃迁到 f
0
1 p 1
p 1 f
n1
2
kT
2n
1
1 22n1
2n
d 2n
d
2n f
p 1 f
2 2
6
4
4
9
UESTC
应用积分公式
E
3 5
NE
f
0
1
5
12
2
kT Ef0
2
电子平均能量
E
E N
3 5
EF 0
2
4
kT
kT EF 0
UESTC
4、费米面
k空间中，能量为EF，即半径为 KF
以上能态。但无论温度多高，
T=0 T >0
εf ε
在
能态被粒子占据的几率始终为 1
f
2
。
UESTC
2、电子能量
dE FFD g d
T = 0 电子总能量
EF0
1
5
E0
c
2 d
22 5 cEF0
0
UESTC
T ≠0
积分公式
E
0
e
1 EF / kT 1
c 1 / 2d
金属自由电子理论

金属自由电子理论

金属自由电子理论文档编制序号：[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]第四章金属自由电子理论1.金属自由电子论作了哪些假设得到了哪些结果解：金属自由论假设金属中的价电子在一个平均势场中彼此独立，如同理想气体中的粒子一样是“自由”的，每个电子的运动由薛定谔方程来描述；电子满足泡利不相容原理，因此，电子不服从经典统计而服从量子的费米－狄拉克统计。

根据这个理论，不仅导出了魏德曼－佛兰兹定律，而且而得出电子气对晶体比热容的贡献是很小的。

2.金属自由电子论在k空间的等能面和费米面是何形状费米能量与哪些因素有关解：金属自由电子论在k空间的等能面和费米面都是球形。

费米能量与电子密度和温度有关。

3.在低温度下电子比热容比经典理论给出的结果小得多，为什么解：因为在低温时，大多数电子的能量远低于费米能，由于受泡利原理的限制基本上不能参与热激发，而只有在费米面附近的电子才能被激发从而对比热容有贡献。

4.驰豫时间的物理意义是什么它与哪些因素有关解：驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间，它的引入是用来描写晶格对电子漂移运动的阻碍能力的。

驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。

5.当2块金属接触时，为什么会产生接触电势差解：由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同，所以这2块金属接触时，会产生接触电势差。

6.已知一维金属晶体共含有N 个电子，晶体的长度为L ，设0=T K 。

试求：（1）电子的状态密度； （2）电子的费米能级； （3）晶体电子的平均能量。

解：(1)该一维金属晶体的电子状态密度为：dEdkdk dZ dE dZ E ⋅==)(ρ (1)考虑在k 空间中，在半径为k 和dk k +的两线段之间所含的状态数为：dk Ldk dZ π=∆=k 2 (2)又由于 mk E 222 =所以mkdk dE 2 = …………………………（3） 将（2）和（3）式代入（1）式，并考虑到每个状态可容纳2个自旋相反的电子，得该一维金属晶体中自由电子的状态密度为：EmLE 22)(πρ= (4)（2）由于电子是费米子，服从费米—狄拉克统计，即在平衡时，能量为E 的能级被电子占据的几率为：11)(+=-TK E E B F eE f (5)于是，系统中的电子总数可表示为：⎰∞=0)()(dE E E f N ρ (6)由于0=T K ，所以当0F E E >，有0)(=E f ，而当0F E E ≤，有1)(=E f ，故（6）式可简化为：⎰=)(FE dE E N ρ＝⎰0022FE dE E m L π＝240FmE L π由此可得：222208mLN E Fπ= …………………………（7） （3）在0=T K 时，晶体电子的平均能量为： ⎰∞=0)()(1dEE E Ef N E ρ＝dE EmL E N FE 2210⎰⋅π＝230)(232F E m N L π＝022223124F E mLN = π 7.限制在边长为L 的正方形中的N 个自由电子，电子的能量为)(2),(222y x y x k k mk k E += 。

固体物理知识点总结 第四章

固体物理知识点总结 第四章

第四章 金属自由电子理论 总
电子气的热容量 功函数和接触电势差
结
自由电子气的能量状态
自由电子气的能量状态
一、自由电子气的能量状态 1.自由电子气(自由电子费米气体)：是指自由的、无相互 ：是指自由的、 作用的、遵从泡利原理的电子气。 作用的、遵从泡利原理的电子气。 2.自由电子气的能量
2πnx kx = L ; 2πny ; ky = L k = 2πnz ; z L
−( E0 −EF )
4πem j＝ 3 (kBT)2 e h
3.接触电势
kBT
= AT e
2 −ϕ kBT
两块不同的金属A 两块不同的金属A和Ｂ相接触，或用导线连接起来，两块 相接触，或用导线连接起来， 金属就会彼此带电产生不同的电势V 称为接触电势。 金属就会彼此带电产生不同的电势 A和VB，称为接触电势。
1 VA − VB = ( ϕ B −43; C = γT + bT
e V a V
3
π2 k２ R 2 B ＝ π Z γ = N0 Z 0 2 EF 2T 0 F
12 Rπ4 b= 3 5 θD
功函数和接触电势差
1.功函数： 电子在深度为E 的势阱内，要使费米面上的电子逃离金属， 电子在深度为 0的势阱内，要使费米面上的电子逃离金属， 的能量， 称为脱出功又称功函数。 至少使之获得ϕ=E0－ＥＦ的能量，ϕ称为脱出功又称功函数。 2.里查逊—德西曼公式
h2k 2 h2 2 2 E= (kx + k 2 + kz ) = y 2m 2m
3.能态密度
∆Z dZ N(E) = lim = E dE ∆E→0 ∆
自由电子气的能态密度
dZ = cE1 2 N(E) = dE
第四章-能带理论-(Band-Theory)

第四章-能带理论-(Band-Theory)

能带理论 - 3 （Band Theory）
近自由电子适用于价电子束缚较弱的金属晶体, 采用赝 势方法后也可以用来研究半导体的价带和导带；对于价电子 束缚较强的半导体和绝缘体, 通常采用紧束缚近似 (TightBinding Approximation, TBA) 来讨论其电子结构.
1
与利用平面波描写零级近似状态的近自由电子 近似不同, 紧束缚近似中首先把电子看作所属原子 的电子, 晶体环境对电子的影响则作为微扰处理.
N
2
V
2
3
4
3
kF2
kF
3 2n 1/3 .
Fermi 球的表面称为 Fermi 面, Fermi 面的能量
称为Fermi 能 (级). Fermi 能对应的动量和速度分称
为 Fermi 动量和 Fermi 速度.
15
一方面, 三维晶体的能量作为简约波矢的函数, 随波矢方向变换而性质有所变化; 另一方面, 三维BZ 构造复杂, 讨论起来比较困难.
由于对称性的存在, 实际上人们并不需要研究整 个BZ (FBZ). 利用对称性, 人们可以通过研究部分 FBZ的情况来了解整个FBZ.
16
晶体全部对称操作的集合构成空间群.
26
原子中的电子能级是分立的, 可以具体表明各能 级的能量. 固体中, 电子能级形成准连续的能带, 标明 每个能级很困难也没有必要. 这时通常引入能态密度 来描写能级的分布：
状态数
能态密度： N E lim Z
E0 E
能量间隔
27
k 空间等能面 E 和 E + ΔE 之间的状态数为
Z
2V
V
当 取遍晶体所属点群中的所有对称操作, 得到一组
k , 它们是等价的, 称为 k*.
固体物理学—课程介绍

固体物理学—课程介绍

12
商业网站
网易公开课 搜狐课堂 / 新浪公开课 / 优酷公开课 /open
13
其他学习资源
（） （维基英文版） 科学网论坛 小木虫论坛
complex forms of matter, in particular to liquid
crystals and polymers".
“founding father of soft matter”27
固体与晶体
橡胶
石蜡
➢ A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an ordered pattern extending in all three spatial dimensions. ➢ In addition to their microscopic structure, large crystals are usually identifiable by their macroscopic geometrical shape, consisting of flat faces with specific, characteristic orientations.
31
晶体的外形与微观结构
32
单晶冰糖和多晶冰糖
/AMuseum/crystal/index.html 33
身边的多晶体
硬币
alloy
瓷器
高岭土
石头
螺钉
上釉
1200℃
陶器
粘土
石头
800-1000℃ /AMuseum/crystal/index.html
第四章金属自由电子理论

第四章金属自由电子理论


dE
之间时，
k
空间中，在半径为
k
和
k

dk的两球
面之间所含的状态数为：
dZ '

4k 2dk k

Vc 8 3
4k 2dk

1 2
(
2m 2
)
3
2
E
1 2
dE
考虑自旋的二重简并dZ 2dZ '
(E)
所以： ( E )

Vc 2 2
(
2m
)
3
2
E
1 2

1
CE 2
其中
C

及其缺陷。
1)由Drude模型导出了欧姆定律，并得到电导的定量表达式，在 解释碱金属的导电性上取得了完全的成功
但是，按Drude模型，碱土金属（二价）的自由电子密度n为碱金属 （一价）的两倍，由式（1-6），电导率σ也应高一倍。但实际上， 碱土金属的导电性不及碱金属，说明Drede模型的局限性。
1
3 维德曼一夫兰兹定律 Wiedemann-Franz Law
k
0 F

3n 2
3
由电子动量
k
0 F
mvF0
得绝对零度时的费米速度矢为: vF0

k
0 F
m
与费米能量对应的热运动温度称为费米温度,记为
所以绝对零度时的费米温度为:
TF0

EF0 kB
TF
.有: kBTF0

EF0
例如铜:铜是面心立方晶体,晶格常数 a 3.611010 m .
每个铜原子电离时放出一个自由电子,所以铜的电子浓度为:
第四章 金属键

第四章 金属键


导体、半导体和绝缘体
晶体按导电性能的高低可以分为
导体 半导体 绝缘体
它们的导电性能不同，
是因为它们的能带结构不同。
导体
导体
Eg
导体
半导体
绝缘体 Eg
Eg
导体 在外电场的作用下，大量共有化电子很 易获得能量，集体定向流动形成电流。 E
从能级图上来看，是因为其共有化电子 很易从低能级跃迁到高能级上去。
上面介绍的是最早提出的经典自由电子理论.1930年前后,由于将量子 力学方法应用于研究金属的结构,这一理论已获得了广泛的发展.在金 属的物理性质中有一种最有趣的性质是,包括碱金属在内的许多金属 呈现出小量的顺磁性,这种顺磁性的大小近似地与温度无关.泡利曾在 1927年对这一现象进行探讨,正是这一探讨开辟了现代金属电子理论 的发展.它的基本概念是:在金属中存在着一组连续或部分连续的“自由 电子能级.在绝对零度时,电子(其数目为N个)通常成对地占据N/2个最 稳定的能级.按照泡利不相容原理的要求,每一对电子的自旋方向是相 反的;这样,在外加磁场中,这些电子的自旋磁矩就不能有效地取向.当 温度比较高时,其中有一些配对的电子对被破坏了,电子对中的一个电 子被提升到比较高的能级.未配对的电子的自旋磁矩能有效地取向, 所以使金属具有顺磁性.未配对电子的数目随着温度的升高而增多; 然而,每个未配对电子的自旋对顺磁磁化率的贡献是随着温度的升高 而减小的.对这二种相反的效应进行定量讨论,解释了所观察到的顺磁 性近似地与温度无关.
设孤立原子的一个能级 Enl ，它最多能容纳 2 (2 l +1) 个电子。 这一能级分裂成由 N条能级组成的能带后，能带最多 能容纳 2N(2l +1)个电子。
2N(2l+1)
第四章 第一节 布洛赫定理

第四章 第一节 布洛赫定理


该方程可以在一个正点阵元胞内求解，属于在有 限区域内的厄米本征值问题，应该有无穷多分立 的本征值E n(k)，对应无穷多的本征函数。
2. 对于一个确定的n， 能量本征值和波函
数都是k的周期函数
我们注意到
其中 将
仍然是正点阵的周期函数 代入能量本征值方程，得到
对比
它们完全相同，因此
即
有相同的本征值，即
对所有具有时间反演对称性的晶体能谱有：
由式子4.1.20有
两边取共轭，k -> -k
能量本征值必须是实数：
结果
满足同一方程，有
5. 等能面垂直于布里渊区界面
等能面定义为k空间，所有能量相等的k构成的曲面。
布里渊区界面是K h的中垂面，因此相对于K h 和-K h的一对布里渊区界面有镜面反演对称。 设A，B为布里渊区界面上关于m对称的两个点，a, b为 布里渊区界面上关于m对称的两个点。它们之间正好 相差一个倒格矢K h。 过a,b两点等能面的法线为
这就是布洛赫定理。
当平移晶格矢量R时，同一能量本征值的波函数只增 加一个相位因子。
注意：不是R的周期函数！
布洛赫定理的另一种表达形式： 周期势场中的单电子波函数可以写成一个调幅的 平面波（布洛赫波函数）：
其中调幅因子u满足R的周期性：
很显然，该函数必然满足布洛赫定理
与自由电子波函数相比，周期场的作用只是用一 个调幅平面波取代了平面波，称为布洛赫波。
平移算符
晶体最重要的特征是平移对称性，定义三个基本的 平移算符： 对任一函数：
它们是可对易的：
同时，平移算符 也是可对易的：
与哈密顿
即
这四个算符具有相同的本征函数，可以用它们所对 应的本征值的量子数来标志周期中的单电子态。
金属自由电子理论

金属自由电子理论

金属自由电子理论Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】第四章金属自由电子理论1.金属自由电子论作了哪些假设得到了哪些结果解：金属自由论假设金属中的价电子在一个平均势场中彼此独立，如同理想气体中的粒子一样是“自由”的，每个电子的运动由薛定谔方程来描述；电子满足泡利不相容原理，因此，电子不服从经典统计而服从量子的费米－狄拉克统计。

根据这个理论，不仅导出了魏德曼－佛兰兹定律，而且而得出电子气对晶体比热容的贡献是很小的。

2.金属自由电子论在k空间的等能面和费米面是何形状费米能量与哪些因素有关解：金属自由电子论在k空间的等能面和费米面都是球形。

费米能量与电子密度和温度有关。

3.在低温度下电子比热容比经典理论给出的结果小得多，为什么解：因为在低温时，大多数电子的能量远低于费米能，由于受泡利原理的限制基本上不能参与热激发，而只有在费米面附近的电子才能被激发从而对比热容有贡献。

4.驰豫时间的物理意义是什么它与哪些因素有关解：驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间，它的引入是用来描写晶格对电子漂移运动的阻碍能力的。

驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。

5.当2块金属接触时，为什么会产生接触电势差解：由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同，所以这2块金属接触时，会产生接触电势差。

6.已知一维金属晶体共含有N 个电子，晶体的长度为L ，设0=T K 。

试求：（1）电子的状态密度；（2）电子的费米能级；（3）晶体电子的平均能量。

解：(1)该一维金属晶体的电子状态密度为：dE dk dk dZ dE dZ E ⋅==)(ρ …………………………（1） 考虑在k 空间中，在半径为k 和dk k +的两线段之间所含的状态数为：dk L dk dZ π=∆=k 2 (2)又由于 mk E 222 = 所以 mk dk dE 2 = (3)将（2）和（3）式代入（1）式，并考虑到每个状态可容纳2个自旋相反的电子，得该一维金属晶体中自由电子的状态密度为：Em LE 22)( πρ= …………………………（4） （2）由于电子是费米子，服从费米—狄拉克统计，即在平衡时，能量为E 的能级被电子占据的几率为： 11)(+=-T K E E B Fe E f (5)于是，系统中的电子总数可表示为：⎰∞=0)()(dE E E f N ρ (6)由于0=T K ，所以当0F E E >，有0)(=E f ，而当0F E E ≤，有1)(=E f ，故（6）式可简化为：⎰=00)(FE dE E N ρ ＝⎰0022FE dE E m L π＝240F mE L π 由此可得： 222208mL N E Fπ= …………………………（7） （3）在0=T K 时，晶体电子的平均能量为： ⎰∞=00)()(1dE E E Ef N E ρ＝dE Em L E N FE 22100⎰⋅ π＝230)(232F E m N L π＝022223124F E mL N = π 7.限制在边长为L 的正方形中的N 个自由电子，电子的能量为)(2),(222y x y x k k mk k E += 。

《凝聚态物理》第四章_能带理论-II


第四章 能带论－2
一、模型的描述：波包
按量子力学，电子用波来描述。经典粒子性要求确定的 轨道、动量。如何把电子的粒子性与波动性联系和统一 起来呢？
量子——经典类比，用到“波包”的概念
▪ 波包：是分布在空间有限区域的波列，频率也有
一定的分布范围。 粒子空间分布在 r 附近 △r 范围内，动量取值
NC
C
gC
e d C KBT
PV
g V
V
e d V KBT
C
V
T的缓 变函数
E
CB
VB
f (E)
第四章 能带论－2
4、半导体的统计理论
本征半导体：
nC pv
c
v
2
1 2
kBT
ln
Pv Pc
E
CB
C
V
VB
f (E)
4-2 恒定电场、磁场作用下
电子的运动
九、恒定磁场 作用下电子的 准经典运动
例：自由电子，B=(0,0,B)
kz
B
运动轨道为圆－回旋运动
回旋周期：
T d k d k d t
2 k 2 m
kx
evB eB
回旋频率：
c
eB m
k
ky
等能面
等于实空间的 回旋频率
第四章 能带论－2
二、自由电子回旋运动（实空间）
m dv dt ev B
vvxy
eB mvy eB mvx
能带电子？由于晶格的散射，电子不可能被无 限制加速
第四章 能带论－2
二、k－空间运动
▪ 电子的运动保持在同一个能带内，能量周期性 变化，在 K－空间周期性运动。

第四章 金属键


各相邻分子轨道间的能级非常接近。它们实际上连成一片， 构成了一个具有一定能量界限（即一定宽度）的能带。能 带的下半部充满电子，上半部则空着。就是金属钠结构论
该理论将整块金属当作一个巨大的分子，晶体中N个原子的每一种 能量相等的原子轨道，通过轨道叠加、线性组合得到N个分子轨道， 它是一组扩展到整块金属的离域轨道。由于N 数值很大（Avogardo 常数数量级），所得分子轨道各能级间的间隔极小，形成一个能带。 每一个能带有一定的能量范围，相邻原子间轨道重叠少的内层原子 轨道形成的能带较窄；轨道重叠多的外层原子轨道形成的能带较宽。 各个能带按能量高低排列起来，成为能带结构。
导体、半导体和绝缘体
晶体按导电性能的高低可以分为
导体 半导体 绝缘体
它们的导电性能不同，
是因为它们的能带结构不同。
导体
导体
Eg
导体
半导体
绝缘体 Eg
Eg
导体 在外电场的作用下，大量共有化电子很 易获得能量，集体定向流动形成电流。 E
从能级图上来看，是因为其共有化电子 很易从低能级跃迁到高能级上去。
二,金属键理论及其对金属通性的解释
一切金属元素的单质,或多或少具有下述通性: 有金属光泽,不透明,有良好的导热性与导电性,有延性和展性,熔点 较高(除汞外在常温下都是晶体),等等. 这些性质是金属晶体内部结构的外在表现.
1916年 ,荷兰理论物理学家洛伦兹(Lorentz,H.A.1853-1928)提出金属 "自由电子理论",可定性地阐明金属的一些特征性质.这个理论认为, 在金属晶体中金属原子失去其价电子成为正离子,正离子如刚性球体 排列在晶体中,电离下来的电子可在整个晶体范围内在正离子堆积的 空隙中“自由”地运行,称为自由电子.正离子之间固然相互排斥,但可 晶体中自由运行的电子能吸引晶体中所有的正离子,把它们紧紧地“结 合”在一起.这就是金属键的自由电子理论模型. 根据上述模型可以看出金属键没有方向性和饱和性. 这个模型可定性地解释金属的机械性能和其它通性.

2023年大学_固体物理基础第三版(阎守胜著)课后题答案下载

2023年固体物理基础第三版（阎守胜著）课后题答案下载固体物理基础第三版（阎守胜著）课后答案下载第一章金属自由电子气体模型1.1 模型及基态性质1.1.1 单电子本征态和本征能量1.1.2 基态和基态的能量1.2 自由电子气体的热性质1.2.1 化学势随温度的变化1.2.2 电子比热1.3 泡利顺磁性1.4 电场中的`自由电子1.4.1 准经典模型1.4.2 电子的动力学方程1.4.3 金属的电导率1.5 光学性质1.6 霍尔效应和磁阻1.7 金属的热导率1.8 自由电子气体模型的局限性第二章晶体的结构2.1 晶格2.1.1 布拉维格子2.1.2 原胞2.1.3 配位数2.1.4 几个常见的布拉维格子2.1.5 晶向、晶面和基元的坐标2.2 对称性和布拉维格子的分类2.2.1 点群2.2.2 7个晶系2.2.3 空间群和14个布拉维格子2.2.4 单胞或惯用单胞2.2.5 二维情形2.2.6 点群对称性和晶体的物理性质 2.3 几种常见的晶体结构2.3.1 CsCl结构和立方钙钛矿结构 2.3.2 NaCl和CaF、2结构2.3.3 金刚石和闪锌矿结构2.3.4 六角密堆积结构2.3.5 实例，正交相YBa2Cu307-82.3.6 简单晶格和复式晶格2.4 倒格子2.4.1 概念的引入2.4.2 倒格子是倒易空间中的布拉维格子 2.4.3 倒格矢与晶面2.4.4 倒格子的点群对称性2.5 晶体结构的实验确定2.5.1 X射线衍射2.5.2 电子衍射和中子衍射2.5.3 扫描隧穿显微镜第三章能带论I3.1 布洛赫定理及能带3.1.1 布洛赫定理及证明3.1.2 波矢七的取值与物理意义3.1.3 能带及其图示3.2 弱周期势近似3.2.1 一维情形3.2.2 能隙和布拉格反射3.2.3 复式晶格3.3 紧束缚近似3.3.1 模型及计算3.3.2 万尼尔函数3.4 能带结构的计算3.4.1 近似方法3.4.2 n(K)的对称性3.4.3 n(K)和n的图示3.5 费米面和态密度3.5.1 高布里渊区3.5.2 费米面的构造3.5.3 态密度第四章能带论Ⅱ4.1 电子运动的半经典模型 4.1.1 模型的表述4.1.2 模型合理性的说明4.1.3 有效质量4.1.4 半经典模型的适用范围4.2 恒定电场、磁场作用下电子的运动4.2.1 恒定电场作用下的电子4.2.2 满带不导电4.2.3 近满带中的空穴4.2.4 导体、半导体和绝缘体的能带论解释 4.2.5 恒定磁场作用下电子的准经典运动 4.3 费米面的测量4.3.1 均匀磁场中的自由电子4.3.2 布洛赫电子的轨道量子化4.3.3 德哈斯一范阿尔芬效应4.3.4 回旋共振方法4.4 用光电子谱研究能带结构4.4.1 态密度分布曲线4.4.2 角分辨光电子谱测定n(K)4.5 一些金属元素的能带结构4.5.1 简单金属4.5.2 一价贵金属4.5.3 四价金属和半金属4.5.4 过渡族金属和稀土金属第五章晶格振动5.1 简谐晶体的经典运动5.1.1 简谐近似5.1.2 一维单原子链，声学支 5.1.3 一维双原子链，光学支 5.1.4 三维情形5.2 简谐晶体的量子理论5.2.1 简正坐标5.2.2 声子5.2.3 晶格比热5.2.4 声子态密度5.3 晶格振动谱的实验测定 5.3.1 中子的非弹性散射5.3.2 可见光的非弹性散射 5.4 非简谐效应5.4.1 热膨胀5.4.2 晶格热导率第六章输运现象6.1 玻尔兹曼方程6.2 电导率6.2.1 金属的直流电导率6.2.2 电子和声子的相互作用 6.2.3 电阻率随温度的变化 6.2.4 剩余电阻率6.2.5 近藤效应06.2.6 半导体的电导率6.3 热导率和热电势6.3.1 热导率6.3.2 热电势6.4 霍尔系数和磁阻第七章固体中的原子键合7.1 概述7.1.1 化学键7.1.2 晶体的分类7.1.3 晶体的结合能7.2 共价晶体7.3 离子晶体7.3.1 结合能7.3.2 离子半径7.3.3 部分离子部分共价的晶体7.4 分子晶体、金属及氢键晶体7.4.1 分子晶体7.4.2 量子晶体7.4.3 金属……第八章缺陷第九章无序第十章尺寸第十一章维度第十二章关联固体物理基础第三版（阎守胜著）：基本信息阎守胜，1938生出生，1962年毕业于北京大学物理系，现任北京大学物理学院教授，博士生导师，兼任中国物理学会《物理》杂志主编，他长期从事低温物理，低温物理实验技术，高温超导电性物理和介观物理方面的实验研究，并讲授大学生的固体物理学，低温物理学和现代固体物理学等课程。

05 金属自由电子气体模型


ε mol
=
N
A
⎜⎛ ⎝
3 2
k
BT
⎞⎟ ⎠
=
3 RT 2
一价金属：CVe ,mol
=
∂ε mol ∂T
=
3R 2
高温时金属的总比热容：
CV
=
C Ph V ,mol
+ CVe ,mol
= 3R + 3 R ≈ 37.40J / mol ⋅ K 2
实际
Ce V，mol
小于经典值
量子：
CVe
~
T TF
常温下：电子的贡献比例很小
kx
=
2π L
nx
ky
=
2π L
ny
kz
=
2π L
nz
nx , ny , nz--一组整数
自由电子的能量是不连续的，相邻能级相距很近. 5 kv空间与态密度 (k-space) 电 的子 端的 点状 代态 表由 一波 个矢可确 能定 的。kv 在 值。kv空相间邻中 代， 表每 点一 在波 三矢 维坐kv
vy
=
−
eτ m
Ey
+
ωcτv x
ωc
=
eB m
--回旋频率
vz
=
−
eτ m
Ez
30
5
Jv = −nevv σ = ne2τ m
σ 0 E x = J x + ωcτJ y σ 0 E y = −ωcτJ x + J y
4.4 霍尔效应和磁阻
长方体样品, 沿x轴施加外电场Ex, 存在电流Jx, 在z轴 加磁场B后, 产生洛仑兹力在负y方向作用到电子上.
+1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
要比理想气体的密度高上千倍。如果将每个电子平均占据的
体积等效成球体，其等效球半径 ：
1 n
=
4 3
π
rs3
rs
=
3
4π n
1/3
~ 10−10 m
如此高浓度的电子，仍然可以以自由粒子运动的方式来描 述，是量子力学出现后才得到解释的。
补充知识：微观粒子尺寸习惯上常用玻尔半径（Bohr radius）做单位：
金属的性质：观察和实验得到的认识 1. 高电导率σ；在一定温度以上σ反比于温度 T。
σ (Ω−1 ⋅ m−1) 绝缘体
半导体
金属
室温下
10−16
10−4 −10+5
106 −108
2. 等温条件下，服从欧姆定律： J = σ E
3. 高热导率 κ 。在足够高的温度下热导率与电导率之比等
于一个普适常数乘以温度。
Wiedemann-Franz 定律 ： LT
=
κ
σ
或：=L
= κ σT
π2
3
kB e
2
4. 载流子浓度与温度无关； 5. 在可见光谱区有几乎不变的强的光学吸收；反射率大或
说有金属光泽。 6. 有良好的延展性，可以进行轧制和锻压。
关于金属的理论必须以全面和谐的解释上述性质为准。
高纯Cu的热导率和电导 率的温度依赖性：
温度 T ↑ 电导率 σ↓
热导率 κ ↓
Lorentz常数的变化
（在一定温区内是常数）
绪论中曾指出：从理论上来解释固体的性质并不是一件容 易的事情，因为任何宏观固体都是由很多原子组成的（典型值 是 1023/cm3个原子），而每个原子又是由原子核和众多电子组 成的，所以既便今天我们已经掌握了微观粒子的运动规律，又 有了大型计算机的帮助，但对这样一个复杂的多体问题也仍然 是无法完整求解的，所以我们只能通过各种合理的近似去接近 真实的情况，成功的固体理论都是合理近似的结果。
第四章 金属自由电子论
4.1 经典自由电子论（Drude-Lorentz) 4.2 量子自由电子论（Sommerfeld ） 4.3 金属的热容和顺磁磁化率 4.4 金属的电导率和热导率 4.5 金属的热电子发射和接触电势 4.6 金属的交流电导率和光学性质 4.7 Hall效应和磁致电阻
参考：阎守胜书 第一章 黄昆 书 6.1,6.2 p275 Kittel 8版第6章
= a0 4πm= εe022 0.529 ×10−10 m=0.0529nm
大多数金属自由电子的 rs / a0 在 2 和 3 之间，
碱金属自由电子的 rs / a0 在 3 到 6 之间。
例如Cu的 =n 8.47 ×1028 m−3
= rs ao
2= .67, rs
0.141nm
～1.4 Å
· Drude 模型把金属简单地看成是由自由电子组成的理想气体， 因此可以套用处理理想气体的方法来处理金属的各种特性。
· Drude Model 中的唯一的参量：电子密度（浓度）
n
=NA ×
Zρm
A
=.022 ×1023 ×
Zρm
A
其中 NA是Avogadro常数，Z是每个原子贡献的价电子数目， ρm 是金属的质量密度（kg/m3），A 是元素的原子量。 我们要注意到：对于金属，n 的典型值为1029/m3。这个值
这些成功使自由电子模型得到承认。虽然之后发现经典 模型并不能解释金属比热、顺磁磁化率等多种金属性质，不 过这些困难并不是自由电子模型本身造成的，而是采用经典 气体近似所造成的，改用量子理论矫正自由电子的行为后， 上述困难得到了圆满解决，因此自由电子模型成为固体理论 研究一个成功尝试，是理解金属、特别是简单金属物理性质 的有力工具。它对于固体理论的发展具有很多的启示意义， 我们回顾一下这个发展过程对我们理解固体理论的特点是有 帮助的。
1897年Thomson发现电子，1900年Drude 就大胆地将 当时已经很成功的气体分子运动论用于金属，提出用自由电 子气模型来解释金属的导电性质，他假定：金属晶体内的价 电子可以自由运动，它们在晶体内的行为宛如理想气体中的 粒子，故称作自由电子模型，以此模型可以解释欧姆定律。 几年之后 Lorentz 又假定自由电子的运动速度服从 MaxwellBoltzman分布， 由此解释了 Wiedemann-Franz 定律。
4.1 经典自由电子论（Drude-Lorentz)
从这章开始，我们将集中讨论金属，金属在固体性质的研 究和应用中占据着重要位置：
一百余个化学元素中，在正常情况下，约有75种元素晶体 处于金属态，人们经常使用的合金更是不计其数；
金属因具有良好的电导率、热导率和延展性等特异性质， 最早获得了广泛应用和理论上的关注。
注意：rs 不是电子自身大小！是它在晶体中可以占有的
平均空间。那么密集的电子依然有高度的自由，从
经典观点看是难以理解的。
简单金属Na的晶体模型图：
金属Na：bcc 点阵 a＝4.225×10-10m， 自由Na+离子的半径为：0.98×10-10m; 因此离子实仅占晶体体积的10.5%。
自由电子模型是固体理论的最早尝试，一个非常简单的模 型竟然给出了意想不到的结果，它改变了我们对固体的认识， 也指出了理论上逐步逼近真实情况的途径。它的成功告诉我们： 只有抓住相关问题物理过程的本质，才能作出最恰当的近似， 常常是最简单的模型也能解释很复杂的现象。
P W Anderson：
一个简化模型对于自然界实际状况的见 解，远胜于个别情况的从头计算，这些计算 即便是对的，也往往包含了过多的细节，以 至于掩盖了而不是显示了现实，计算或测量 的过于精细有时不一定是优点，反而可能是 缺点，因为人们精确测量或计算出的结果往 往是与机制无关的事情，总之，完美的计算 可以重视自然，但不能解释它。
尝试对金属特性的理解（自由电子论和能带论）既是现代 固体理论的起步，也是现代固体理论的核心内容，而且对金属 性质的理解也是对非金属性质理解的基础。
自由电子论在解释金属性质上获得了相当的成功，虽然之 后发展起来的能带论，适用范围更具有普遍性，理论说明更加 严格，定量计算的结果更符合实际，但由于自由电子论的简明 直观特点，直到今天依然常被人们所利用，所以我们和黄昆书 的安排有所不同，仍把自由电子论作为独立的章节，按照发展 的顺序，放到能带论之前讲述。由于自由电子论并不需要晶体 结构的知识，因此也有些教材把它放在最前面作为引言讲授。