哈工大自动控制原理设计
- 格式:doc
- 大小:968.00 KB
- 文档页数:22




机械设计制造及其自动化专业课程介绍默认分类 2010-04-24 11:35:19 阅读61 评论0 字号:大中小订阅作者:船舶学院时间:2009-6-16 14:40:51“机电系统计算机控制”教学大纲(PUTER CONTROL OF ELECTRICAL MACHINE SYSTEMS)大纲编制:李哲教研室主任:李哲课程编码:课程名称:机电系统计算机控制教学性质:选修课适用专业:机械及近机类专业学时:30(26/4)学分:1.5一、课程的性质、目的与任务本课程是适应机电一体化的发展趋势而设立的,是机械设计制造及自动化专业的一门主干课程,主要讲述直流电机、交流电机控制系统,液压伺服控制系统和气压传动控制系统,通过这门课让学生掌握机电液气系统的设计和应用。
二、课程的基本要求本课程主要讲授内容有直流、交流电机的组成、原理、动态特性及其应用,液压伺服系统设计与气压传动系统设计;要求学生掌握机电液气系统的组成、分类,分析和设计;了解各自的特点和应用场合;具备分析机电液气系统和设计简单的机电液气系统的能力,为进一步学习深造和适应未来的工作奠定基础。
三、本课程与相关课程的联系与分工相关课程有:电工学、模拟电路、自动控制原理、液压传动;电工学、模拟电路、自动控制原理等课程作为本课程的基础课。
液压传动课程侧重于讲述液压传动系统,本课程侧重于液压控制系统。
四、教学大纲内容使用教材与参考教材1、使用教材:(骆涵秀主编机电控制 XX大学 2000年1月)2、参考教材:(李洪人液压控制系统国防工业)(邓星钟机电传动控制机械工业)(朱善君可编程控制器系统原理应用维护清华大学)五、教学大纲内容及学时分配第一章概述(2)本章主要内容有:分别用实例引出机电、液压、气动控制系统的整体组成,功能和特点;要求学生掌握机电液气系统的组成;了解机电液气系统的发展方向和选用原则。
第二章直流电机(4)本章主要内容有:直流电机的原理,动态特性分析和系统应用;要求学生掌握直流电机的机械特性和系统应用;了解直流电机的原理、组成。

考查要点:一、控制系统的数学模型1、控制系统运动的建立;2、控制系统的传递函数的概念及求取、方框图及其简化、信号流图及梅森公式。
二、线性系统的时域分析1、一阶、二阶系统的时域分析;2、线性系统的稳定性基本概念及熟练掌握劳斯 (Routh)稳定判据判别稳定性的方法;3、控制系统稳态误差分析及其计算方法;4、复合控制。
三、根轨迹法1、根轨迹、根轨迹方程及其绘制根轨迹的基本规则;2、理解控制系统根轨迹分析方法。
四、频率响应法1、线性系统频率响应物理意义及其描述方法;2、典型环节的频率响应(幅相曲线与对数频率特性曲线);3、开环系统及闭环系统的频率响应的绘制;4、奈奎斯特(Nyquist)稳定判据和控制系统相对稳定性;5、频域指标与时域指标的关系。
五、控制系统的校正与综合1、频率响应法串联校正分析法设计;2、基于频率响应法的串联、反馈校正的综合法设计。
六、非线性控制系统的分析1、了解典型非线性特性的输入输出关系(数学表达及关系曲线);2、理解非线性环节对线性系统的影响;3、相平面法、描述函数法分析非线性控制系统。
七、数字控制系统的普通概念1、采样过程、采样定理、零阶保持器的基本概念。
八、数字控制系统1、Z 变换的基本概念、基本定理及 Z 反变换;2、数字控制系统的数学描述;3、数字控制系统稳定性分析;4、数字控制系统的暂态、稳态、误差分析。
5、数字控制系统的离散化设计方法及至少拍离散系统设计。
九、线性系统的状态空间描述1、线性时不变系统状态空间描述;2、线性定常系统的运动分析、状态转移阵、脉冲响应阵;3、线性离散系统的状态空间描述;4、线性系统的能控性和能观性判别方法。
十、线性定常系统的线性变换1、状态空间表达式的线性变换;2、对偶性原理;3、线性系统的结构分解。
十一、李雅普诺夫稳定性分析1、李亚普诺夫意义下运动稳定性的基本概念;2、李亚普诺夫第二法主要定理;3、系统运动稳定性判据。
十二、线性反馈系统的时间域综合1、状态反馈和输出反馈;2、极点配置的设计方法;3、状态观测器的设计;4、状态观测器和状态反馈组合系统。




H a r b i n I n s t i t u t e o f T e c h n o l o g y课程设计说明书(论文)课程名称:自动控制理论课程设计设计题目:直线一级倒立摆控制器设计院系:电气工程及其自动化学院班级:设计者:学号:指导教师:**哈尔滨工业大学哈尔滨工业大学课程设计任务书*注:此任务书由课程设计指导教师填写。
1、理论模型建立和分析1.1直线一级倒立摆数学模型的推导对于忽略空气阻力和各种摩擦之后,直线一级倒立摆系统抽象为小车和匀质杆组成的系统。
xbp图1-1 倒立摆系统小车和摆杆的受力分析本系统参数定义如下:M——小车质量;m——摆杆质量。
b——小车摩擦系数;l——摆杆转动轴心到杆质心的长度;I——摆杆惯量;F——加在小车上的力;x——小车位置;φ——摆杆与垂直向上方向的夹角。
θ——摆杆与垂直向下方向的夹角方程为:Mx F bx N=--(1-1)因此主动控制力可近似线性化地表示为:()22sin d N m x l dtθ=+ (1-2)即:2cos sin N mx ml ml θθθθ=+- (1-3)代入前面式子:()2cos sin M m x bx ml ml F θθθθ+++-= (1-4)垂直方向上:()22cos d P mg m l dt θ-=- (1-5)即:2sin cos P mg ml ml θθθθ-=+ (1-6) 力矩平衡方程:sin cos Pl Nl I θθθ--= (1-7)注意等式前面的负号,由于,cos cos ,sin sin θπφφθφθ=+=-=-()22sin cos I ml mgl mlxθθθ++=- (1-8)1.微分方程模型 设θπφ=+,近似处理:2cos 1,sin ,()0d dtθθθφ=-=-= 设u=F ,则:()()2M m x bx ml u I ml mgl mlx φφφ⎧++-=⎪⎨+-=⎪⎩ (1-9)2.传递函数模型对上式拉氏变换处理,设初始条件为0,则:()()22222()()()()()()()M m X s s bX s ml s s U s I ml s s mgl s mlX s s ⎧++-Φ=⎪⎨+Φ-Φ=⎪⎩(1-10) 输出为角度为φ,由第二式得到()22()()I ml g X s s ml s ⎡⎤+⎢⎥=-Φ⎢⎥⎣⎦ (1-11)或者()222()()s mls X s I ml s mglΦ=+- (1-12)如果令x ν=,则有()22()()s mlV s I ml s mglΦ=+- (1-13)把上式代入10式,则有:()()()22222()()()()I ml I ml g g M m s s b s s ml s s U s ml s ml s ⎡⎤⎡⎤++⎢⎥⎢⎥+-Φ++Φ-Φ=⎢⎥⎢⎥⎣⎦⎣⎦(1-14)整理:()()212432()()()ml s s q G s U s b I ml M m mgl bmgl s s s sqqqΦ==+++--(1-15)其中()()()22q M m I ml ml ⎡⎤=++-⎣⎦从而,有()()()()()222222432222432()()()()()X s s G s s U s ml s I ml s mglq mlsb I ml M m mgl bmgl s s s s qqqI ml mgls q q b I ml M m mgl bmgl s s s sqqqΦ=⨯Φ+-=⨯+++--+-=+++--(1-16)3.状态空间数学模型X AX BuY CX Du=+=+,可得状态方程()()()()()()()()()2222222222x x I ml b I ml m gl x x u I M m Mml I M m Mml I M m Mml mgl M m mlb ml x u I M m Mml I M m Mml I M m Mml φφφφφ=⎧⎪-++⎪=++⎪++++++⎪⎨=⎪⎪+-⎪=++⎪++++++⎩()()()()()()()()()22222222220100000000100010000010x x I ml b I ml m gl x x I M m Mml I M m Mml I M m Mml u mlb mgl M m ml I M m Mml I M m Mml I M m Mmlx y φφφφφ-++++++++=+-+++++++==⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎣⎦⎣⎦00x x uφφ+⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎡⎤⎪⎢⎥⎡⎤⎪⎢⎥⎥⎢⎥⎪⎢⎥⎣⎦⎪⎢⎥⎩⎣⎦1.2系统阶跃响应分析1.2.1、阶跃响应源程序:参考模型 %实际系统参数M=0.5; m=0.2; b=0.1; l=0.3; I=0.006; g=9.8; T=0.005;%求传递函数gs(输出为摆杆角度)和gspo(输出为小车位置)q=(M+m)*(I+m*l^2)-(m*l)^2; num=[m*l/q 0];den=[1 b*(I+m*l^2)/q -(M+m)*m*g*l/q -b*m*g*l/q]; gs=tf(num,den);numpo=[(I+m*l^2)/q 0 -m*g*l/q];denpo=[1 b*(I+m*l^2)/q -(M+m)*m*g*l/q -b*m*g*l/q 0]; gspo=tf(numpo,denpo);%求状态空间sys(A,B,C,D)p=I*(M+m)+M*m*l^2;A=[0 1 0 0;0 -(I+m*l^2)*b/p m^2*g*l^2/p 0;0 0 0 1;0 -m*b*l/p m*g*l*(M+m)/p 0]; B=[0;(I+m*l^2)/p;0;m*l/p]; C=[1 0 0 0;0 0 1 0]; D=0;sys=ss(A,B,C,D);%通过传递函数求系统(摆杆角度和小车位置)的开环阶越响应t=0:T:5; y1=step(gs,t); y2=step(gspo,t); figure(1);plot(t,y2,'b',t,y1,'r'); axis([0 2.5 0 80]);legend('Car Position','Pendulum Angle'); 1.2.2、仿真结果:通过传递函数求系统(摆杆角度和小车位置)的开环阶越响应01020304050607080图1-2 摆杆和小车位置的开环阶跃响应注:左边红色代表小车位置,右边蓝色代表摆杆角度响应。
电气工程及其自动化专业课程设计150kW电力拖动自动控制系统设计学生学号:12345678学生姓名:知行合一班级:123456班指导教师:王阳明起止日期:哈尔滨工程大学自动化学院一、设计要求:(一)基本要求根据所要求指标自选直流调速控制系统进行设计。
1.调速系统能进行平滑地速度调节,负载电机可逆运行,具有较宽地转速调速D≥),系统在工作范围内能稳定工作。
范围(102. 系统静特性良好,理论上实现无静差。
3. 动态性能指标:转速超调量小于5%,电流超调量小于5%,动态最大转速降小于10%。
4. 系统在5%负载以上变化的运行范围内电流连续。
5. 调速系统中设置有过电压、过电流保护,并且能够实现制动运行。
6. 给定信号对应范围控制在±10V之间。
(二)被控对象参数所设计控制系统被控对象参数参考MATLAB/Simulink提供直流电机所提供直流电机的模型的参数。
第10组所选择的直流电机序号20号。
参见下列各图。
(三)硬件电路图设计要求要求实现电流和转速值的显示,转速给定的设置(具有起动、停止、加速、减 速、突加给定、正反转切换功能)基于89c58单片机(双列直插40针)设计一套微机数字监控系统硬件结构,并采用PROTUES 进行单片机系统仿真校验,搭建相应的硬件电路并校验。
外围条件:电力拖动控制系统需要单片机控制系统提供转速给定模拟控制信号(最大转速对应电压信号为5V 或10V );单片机控制系统从电拖控制系统获得 ±5V (或者±10V )之间的转速和电流测量信号。
具体要求如下:硬件结构中包括89c58单片机最小系统;外加AD 转换(采用TLC2543一片)和DA 转换(采用DAC0832一片);两组四位数码管(采用SM420564四位七段数码管)分别用于显示转速(4位有效数字)和电流值(负号和3位有效数字),可以辅助led 灯显示正反转状态,则速度无需显示正负号; 设置对应按键(采用小4脚按键),实现起动、停止、加速、减速、突加给定(包括突加给定设置)、正反转切换控制; 如果需要调理电路,可自行设计添加。
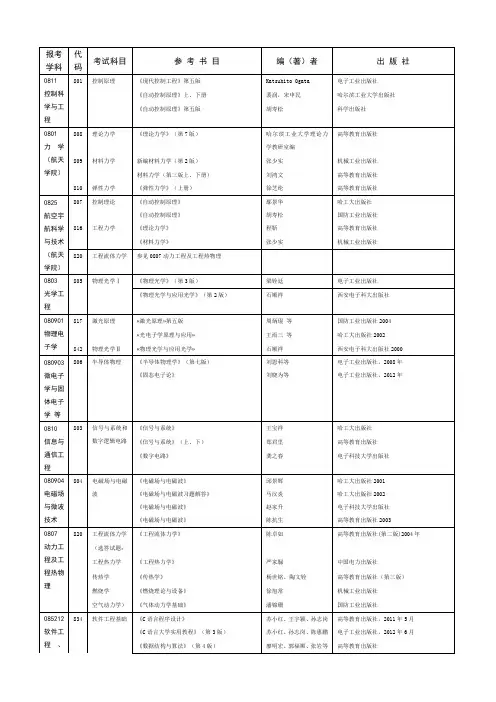
报考学科代码考试科目参考书目编(著)者出版社0811控制科学与工程801 控制原理《现代控制工程》第四版Katsuhito Ogata 电子工业出版社《自动控制原理》上、下册裴润,宋申民哈尔滨工业大学出版社《自动控制原理》第五版胡寿松科学出版社0801力学(航天学院)808 理论力学《理论力学》(第7版)哈尔滨工业大学理论力学教研室编高等教育出版社809 材料力学新编材料力学(第2版)张少实机械工业出版社材料力学(第三版上、下册)刘鸿文高等教育出版社810 弹性力学《弹性力学》(上册)徐芝纶高等教育出版社082501飞行器设计、082504人机与环境工程807 控制理论《自动控制原理》鄢景华哈工大出版社《自动控制原理》胡寿松国防工业出版社816 工程力学《理论力学》程靳高等教育出版社《材料力学》张少实机械工业出版社0803光学工程805 物理光学Ⅰ《物理光学》梁铨廷机械工业出版社《物理光学与应用光学》石顺祥西安电子科大出版社2000080901 物理电子学817 激光原理«激光原理»第五版周炳琨等国防工业出版社2004 «光电子学原理与应用»王雨三等哈工大出版社2002842 物理光学Ⅱ«物理光学与应用光学»石顺祥西安电子科大出版社2000080903微电子学与固体电子学085209集成电路工程806 半导体物理《半导体物理学》(第七版)刘恩科等电子工业出版社,2008年0810信息与通信工程803 信号与系统和数字逻辑电路《信号与系统》王宝祥哈工大出版社《信号与系统》(上、下)郑君里高等教育出版社《数字电路》龚之春电子科技大学出版社080904电磁场与微波技术804 电磁场与电磁波《电磁场与电磁波》邱景辉哈工大出版社2001《电磁场与电磁波习题解答》马汉炎哈工大出版社2002《电磁场与电磁波》赵家升电子科技大学出版社《电磁场与电磁波》陈抗生高等教育出版社20030807动力工程及工程热物820 工程流体力学《工程流体力学》陈卓如高等教育出版社(第二版)2004年(选答试题:工程热力学《工程热力学》严家騄中国电力出版社传热学《传热学》杨世铭、陶文铨高等教育出版社(第三版)理燃烧学《燃烧理论与设备》徐旭常机械工业出版社空气动力学)《气体动力学基础》潘锦珊国防工业出版社085212软件工程834 软件工程基础《软件工程_原理、方法与应用》史济民等高等教育出版社《C程序设计》谭浩强清华大学出版社0804仪器科学与技术826 电子技术基础 1.《模拟电子技术基础》王淑娟高等教育出版社,20102.《数字电子技术基础》杨春玲高等教育出版社,20103.《模拟电子技术基础》(第四版)华成英高等教育出版社,20064.《数字电子技术基础》(第五版)阎石高等教育出版社,20065.《电子技术基础》(模拟部分第五版)康华光高等教育出版社,20066.《电子技术基础》(数字部分第五版)康华光高等教育出版社,20067.《模拟电子技术基础学习指导与考研指南》王淑娟高等教育出版社,2009(第2次印刷)8.《数字电子技术基础学习指导与考研指南》王淑娟高等教育出版社,2010(第3次印刷)注:在(1)(2)(7)(8)、(3)(4)(7)(8)和(5)(6)(7)(8)中任选一套0808电气工程827 电路与数字电子技术电路部分教材:《电路理论基础(第三版)》陈希有高教出版社,2004年《电路(第五版)》邱关源高教出版社,2006年电路部分参考书:《电路考研大串讲》孙立山科学出版社,2006年《电路名师大课堂》,孙立山科学出版社,2006年数字电子技术部分:①《数字电子技术基础》杨春玲高等教育出版社,2010年②《数字电子技术基础》(第五版)阎石高等教育出版社,2006年③《数字电子技术基础》(数字部分第五版)康华光高等教育出版社,2006年④《数字电子技术基础学习指导与考研指南》王淑娟高等教育出版社,2010年,(第3次印刷)注:在(1)(4)、(2)(4)和(3)(4)中任选一套。
哈工大自动控制原理哈工大自动控制原理引言•自动控制原理(Automatic Control Principle)是指利用控制系统对被控对象进行调节、管理和控制的学科。
它广泛应用于各个领域,如机械、电子、航空、化工等。
什么是自动控制原理•自动控制原理是一门研究如何设计、分析和改进控制系统的学科。
它主要研究控制系统的建模、控制方法和控制理论。
控制系统的基本组成•控制系统由四个基本组成部分构成:1.被控对象(Plant):也称为系统,在自动控制中是需要被控制的物理实体或过程。
2.传感器(Sensor):用于测量被控对象的状态或输出信号,并将其转换成电信号。
3.执行机构(Actuator):根据控制器的输出信号,将电信号转换成对被控对象施加的作用力、功率等。
4.控制器(Controller):基于传感器测量值,计算出控制器输出信号,并将其发送给执行机构。
自动控制的基本原理•自动控制的基本原理是建立在数学模型和控制方法上的。
其主要包括以下几个方面:1.系统建模:将被控对象的动态特性转化成数学方程。
常见的建模方法有传递函数法、状态空间法等。
2.稳定性分析:通过数学分析和计算,确定控制系统在各种工况下是否稳定。
常见的稳定性分析方法有根轨迹法、频域法等。
3.控制器设计:基于系统模型和稳定性要求,设计出适合的控制器。
常见的控制器设计方法有比例积分微分控制器(PID)方法、模糊控制方法等。
4.闭环控制:将测量信号通过反馈路径返回给控制器,以实现对被控对象的控制。
闭环控制可以提高系统的稳定性和鲁棒性。
自动控制在工程中的应用•自动控制在工程中有着广泛的应用,以下是一些常见的应用领域:1.工业自动化:包括工厂自动化、流水线控制、机器人控制等。
2.交通运输:包括交通信号灯控制、自动驾驶等。
3.航空航天:包括飞行控制、导航系统等。
4.电力系统:包括发电厂控制、电网调度等。
5.化工过程:包括化工生产、反应控制等。
结语•自动控制原理作为一门学科,研究如何设计和改进控制系统。
H a r b i n I n s t i t u t e o f T e c h n o l o g y课程设计说明书(论文)课程名称:自动控制原理课程设计设计题目:随动系统的校正院系:航天学院班级:设计者:学号:指导教师:设计时间:2014.2哈尔滨工业大学哈尔滨工业大学课程设计任务书*注:此任务书由课程设计指导教师填写。
目录1、题目要求与分析 (1)1.1题目要求 (1)1.2题目分析 (1)2、人工设计 (1)2.1未校正系统的根轨迹 (1)2.2校正环节 (2)2.2.1 串联迟后校正 (2)2.2.2 串联迟后--超前校正 (4)3、计算机辅助设计 (6)3.1对被控对象仿真 (6)3.2对校正以后的系统仿真 (7)3.2.1 串联迟后校正 (7)3.2.2 串联迟后--超前校正 (8)3.3对校正后闭环系统仿真 (9)3.3.1 串联迟后校正 (9)3.3.2 串联迟后--超前校正 (10)4、校正装置电路图 (11)4.1串联装置原理图 (11)4.2校正环节装置电路 (11)4.2.1 串联迟后校正校正装置电路 (11)4.2.2 串联迟后—超前校正装置电路 (13)5、系统校正前后的nyquist图 (15)5.1系统校正前的nyquist图 (15)5.2系统校正后的nyquist图 (15)5.2.1 串联迟后校正的nyquist图 (15)5.2.2 迟后—超前校正的nyquist图 (16)6、设计总结 (16)7.心得体会 (17)1、题目要求与分析 1.1题目要求(1)、已知控制系统固有传递函数如下: G(s)=)1125.0)(15.0(8++S s s(2)、性能指标要求:a. 输入单位速度信号时,稳态误差e<0.15rad.b. 输入单位阶跃信号时,超调量σρ<35%,调整时间t s <10秒。
c.输入单位阶跃信号时,超调量σρ<25%,调整时间t s <4秒。
1.2 题目分析用MALAB 绘制原传递函数的单位阶跃响应图,如下图:0510152025303540-1-0.8-0.6-0.4-0.200.20.40.60.81Step ResponseTime (seconds)A m p l i t u d e由图可知系统超调量为80%,调整时间为25s ,所以不符合要求。
2、人工设计2.1未校正系统的根轨迹由根轨迹图像可知,根轨迹与虚轴交点处的k 值为1.3左右,当k.>1.3时,系统不稳定。
题中k=8 ,因此系统不稳定。
2.2 校正环节系统的开环放大倍数为8,因此系统的稳态误差为1/8=0.125,满足e<0.15rad 。
2.2.1 串联迟后校正当设计要求为输入单位阶跃信号时,超调量σρ<35%,调整时间t s <10秒时,将题目中对闭环系统的动态过程要求转化开环频率特性要求由 .350)1s i n1(.406.10P <-+=γσ 得 ︒≈>4369.42 γ 由 s c10])1sin 1(5.2)1sin 1(5.12[w t 2s <-+-+=γγπ取 69.42>γ=>47.01sin 1=-γ所以得 s rad c /03.1w > 手工做出开环传递函数的bode 图,如附录图1——系统校正前的bode 图 经计算,令1)1125.0)(15.0(8)(=++=jw jw jw jw G ,解得原开环传递函数的剪切频率为 s rad w c /57.3=由)1125.0)(15.0(8)(++=jw jw jw jw G有 79.174125.0arctan 5.0arctan 90)(-=---=∠c c c w w jw G 知 21.5)(180=∠+=c jw G γ 由上面的计算知 )1125.0)(15.0(70)(G 0++=s s s s 剪切频率为s e c/57.3rad w c =,大于设计要求,而相角裕度为deg 21.5=γ,不满足设计要求。
若采用串联超前校正,由于未校正时系统不稳定,且截止频率大于要求值。
在这种情况下,采用串联超前校正是无效的。
若采用串联迟后校正,按式w w jw G 125.0arctan 5.0arctan 90)(0---=∠ 求取满足相角裕度的剪切频率,则 00001271043180)(G -=+︒+-=∠jw即有︒-=---=∠127125.0a r c t a n 5.0ar c t a n 90)(0w w jw G 解得1.1rad/s =w若以 1.1rad/s =w 作为剪切频率,也能满足s rad c /03.1w >的设计指标。
也就是说,只用串联迟后校正即可同时满足相角裕度和剪切频率的设计要求。
设Gc(s)= 11++Ts s τ=11++s s βττ,求β,有20lg|G0 (c j ω) |=20lg β⇒β=6.31取09.911.01011=⇒==ττc w ,T=βτ=57.36。
故迟后校正网络的传递函数为Gc(S)=136.57109.9++s s ,最后得校正后的传递函数为G(s)=)136.57)(1125.0)(15.0()109.9(8++++s s s s 。
检验:手工在对数坐标纸上画出校正以后系统的频率特性bode 图(附录图2——系统校正后的bode 图),经计算,校正以后系统的剪切频率为 s rad c /1.1w = 将 s rad c /1.1w = 代入 )(G jw ∠ 有 )(0c jw G ∠=arctan(9.09cw )-90deg- arctan(0.5cw )- arctan(0.125cw )-arctan(57.36c w )=-131deg所以相角裕度为︒=︒-︒=49131180γ>43deg ,满足设计要求。
2.2.2 串联迟后--超前校正当设计要求为输入单位阶跃信号时,超调量σρ<25%,调整时间t s <4秒时,将题目中对闭环系统的动态过程要求转化开环频率特性要求由 .250)1s i n1(.406.10P <-+=γσ 得 ︒≈>5569.54 γ 由 s c4])1s i n 1(5.2)1s i n 1(5.12[w t 2s <-+-+=γγπ取 69.54>γ=>23.01sin 1=-γ所以得 s rad c /94.1w > 同上一个条件,因为系统不稳定,所以只采用串联超前校正是没有用的。
此时若只采用串联迟后校正,按式w w jw G 125.0arctan 5.0arctan 90)(0---=∠ 求取满足相角裕度的剪切频率,则 00001151055180)(G -=+︒+-=∠jw即有︒-=---=∠115125.0a r c t a n 5.0ar c t a n 90)(0w w jw G 解得0.706rad/s =w若以0.706rad/s =w 作为剪切频率,则不能满足s rad c /94.1w >的设计指标。
也就是说,只用串联迟后校正不能同时满足相角裕度和剪切频率的设计要求。
考虑到串联超前校正可以有效地增加相较裕度,所以,首先采用串联迟后校正,使系统的剪切频率满足或接近于近似满足设计要求。
在此基础上,再采用串联超前校正,使相角裕度满足设计要求。
考虑到串联超前校正时,会使原系统的剪切频率增大,所以在做串联迟后校正时可以使剪切频率略小于设计要求。
首先,取rad/s 1.5=c w ,做串联迟后校正。
当rad/s 1.5=c w 时,代入 =++=)1125.0)(15.0(8)(0c c c c jw jw jw jw G 4.19所以 βlg 20)(lg 200=c jw G 解得串联迟后校正参数 =β 4.19。
取===>=ττc w 1011 6.67 所以 ==βτT 27.95 即迟后环节为 195.27167.6)(1c ++=s s s G由以上计算得串联迟后校正以后的开环传递函数为 195.27167.6)1125.0)(15.0(8)(01++∙++=s s s s s G做出串联迟后校正以后的开环频率特性,如下图。
M a g n i t u d e (d B )10101010101010P h a s e (d e g )Bode DiagramFrequency (rad/sec)由图知,串联迟后校正以后,剪切频率为s rad w c /5.1=,相角裕度为 38=γ 对串联迟后校正以后的系统做串联超前校正。
先求出串联超前校正应提供的相角增量 0000033153855=+-=∆+-=Φγγm故29.033sin 133sin 1sin 1sin 1=+-=Φ+Φ-=m m α44.21lg 20-=-===>α=20lg|G 01(jw )| 所以|G 01(jw )|=0.54,解得w m =2.25rad/s 于是有 ==mw ατ10.83 T=ατ=0.24所以超前环节为 Gc 2=124.0183.0++s s最后得到迟后——超前校正后的开环传递函数 124.0183.0195.27167.6)1125.0)(15.0(8)(++∙++∙++=s s s s s s s G迟后——超前校正网络的传递函数Gc(s)= 124.0183.0195.27167.6++∙++s s s检验:手工在对数坐标纸上画出校正以后系统的频率特性bode 图(附录图3——系统校正后的bode 图),由图知,校正以后系统的剪切频率为 s rad c /25.2w = 将 s rad c /25.2w = 代入 )(G jw ∠ 有)(0c jw G ∠=arctan(6.67c w )+arctan(0.83c w )-90deg- arctan(0.5c w )- arctan(0.125c w )-arctan(27.95c w )- arctan(0.24c w )=-124deg所以相角裕度为︒=︒-︒=56124180λ>55deg ,均满足设计要求。
3、计算机辅助设计 3.1 对被控对象仿真(1)被控对象开环Simulink 模型图图4 原开环传递函数Simulink 模型图 (2)被控对象开环Bode 图-150-100-5050M a g n i t u d e (d B )10-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramGm = 1.94 dB (at 4 rad/sec) , P m = 5.21 deg (at 3.57 rad/sec)Frequency (rad/sec)图5 原开环传递函数Bode 图由仿真结果知,原系统开环传递函数剪切频率为s rad w c /57.3=,相角裕度为deg 21.5=γ,不符合设计要求。