过程能力分析ca计算公式

cpk中的ca计算公式及解释摘要：I.引言- 简要介绍cpk 和ca 的概念- 说明本文的目的和结构II.cpk 和ca 的定义与作用- 解释cpk 和ca 的含义- 说明cpk 和ca 在制程控制中的应用和重要性III.cpk 中的ca 计算公式- 公式：cpkcp(1-ca)- 解释公式中各部分的含义- 说明公式推导过程和计算方法IV.ca 计算公式的解释- 解释ca 的含义和计算方法- 说明ca 与制程准确度、规格中心值的关系- 解释cpk 与ppk 之间的关系和区别V.总结与展望- 总结cpk 和ca 的概念、计算公式及其应用- 展望cpk 和ca 在工业生产中的发展趋势和前景正文：I.引言cpk（Combined Process Capability Index）是衡量制程能力的一种指标，用于评估生产过程的稳定性和产品质量。

在cpk 中，ca（Capability of Accuracy）是一个重要的组成部分，反映了制程的准确度。

本文将详细介绍cpk 中的ca 计算公式及解释。

II.cpk 和ca 的定义与作用cpk 是制程能力的综合指标，表示过程在一定时间内，实际加工能力满足产品质量标准要求的程度。

cpk 的计算公式为：cpk = (USL - LSL) / 6σ，其中USL 表示上限规格，LSL 表示下限规格，σ表示过程标准差。

ca 是制程准确度的一个度量，反映了实际过程平均值与规格中心值的一致性。

在cpk 计算中，ca 的计算公式为：ca = (USL - ML) / (2 * σ)，其中ML 表示最大允许偏差。

III.cpk 中的ca 计算公式在cpk 计算公式中，ca 的计算公式为：cpkcp(1-ca)。

这个公式中，cp 表示过程能力，k 表示过程中心，p 表示过程分布。

1-ca 表示过程分布的尾部概率，即过程在规格范围内的概率。

IV.ca 计算公式的解释ca 计算公式中，USL 表示上限规格，ML 表示最大允许偏差。

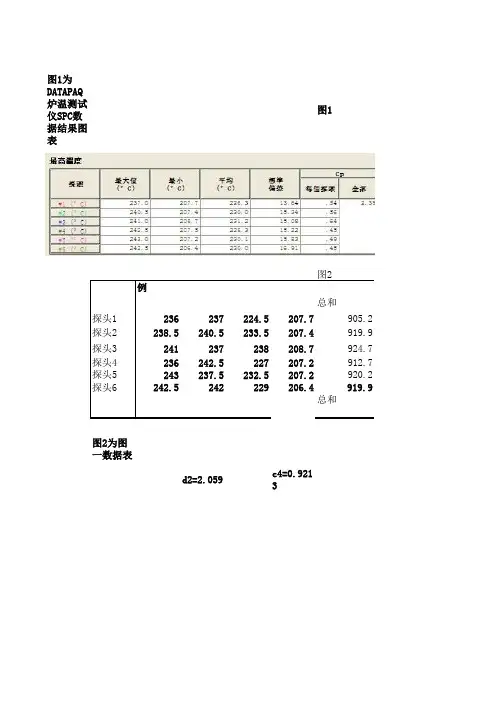
cpk的ca计算公式及解释（最新版）目录1.CPK 的含义与分类2.CPK 计算公式3.CPK 的解释与应用4.制程能力指数及其作用5.CPK 与 PPK 的比较正文一、CPK 的含义与分类CPK，即组合公钥（Combined Public Key），是一种加密算法，以很小的资源，生成大规模密钥。

它主要分为三类：标识密钥、分割钥匙、组合钥匙。

CPK 是制程水平的量化反映，用于衡量工序在一定时间里，处于控制状态（稳定状态）下的实际加工能力。

二、CPK 计算公式CPK 的计算公式为：CPK = Cp(1-Ca)。

其中，Cp 表示过程能力指数，Ca 表示制程准确度，即实际平均值与规格中心值之一致性。

三、CPK 的解释与应用CPK 是一种表示制程水平高低的方便方法，其实质作用是反映制程合格率的高低。

制程能力指数越高，说明制程的稳定性和加工能力越强。

CPK 广泛应用于制造业，尤其是汽车、航空航天等行业，用于评估和改进制造过程的质量和稳定性。

四、制程能力指数及其作用制程能力指数是一种表示制程水平高低的方便方法，其实质作用是反映制程合格率的高低。

它包括两个方面：过程能力指数（Cp）和过程性能指数（Cpk）。

过程能力指数 Cp 表示过程的稳定性和加工能力，而过程性能指数 Cpk 则表示过程的实际性能和制程能力。

Cp 和 Cpk 的计算公式分别为：Cp = T/6σ，其中T表示规格范围，σ表示标准差。

Cpk = min(UCL-Xbar)/3(Xbar-LCL)/3，其中 UCL 表示上限规格，Xbar 表示样本平均值，LCL 表示下限规格。

五、CPK 与 PPK 的比较CPK 和 PPK（过程性能指数）是评估制造过程稳定性和性能的两种常用指标。

它们的主要区别在于计算方法和应用场景。

CPK 主要用于评估过程的稳定性和加工能力，其计算公式为 CPK = Cp(1-Ca)，适用于评估过程的实际性能。

而 PPK 主要用于评估过程的潜在能力，其计算公式为 PPK = T/6σ，适用于评估过程的设计能力。

过程能力CPK的计算方法
Cpk是一种用于量化制程水平的指数，它可以通过一个数
值来反映制程的合格率。

Cpk的计算公式为Cpk=Cp(1-|Ca|)，
其中Ca代表制程准确度，Cp代表制程精密度。

需要注意的是，在计算Cpk时，样本数据至少应有20组，并且数据要具有一
定代表性。

根据Cpk值的大小，可以将制程分为不同的等级。

A+级
表示制程水平非常高，Cpk值大于等于1.67；A级表示状态良好，Cpk值在1.33到1.67之间；B级表示需要改进，Cpk值
在1.0到1.33之间；C级表示制程不良较多，Cpk值在0.67到1.0之间；D级表示制程能力较差，Cpk值小于0.67.
在制程规格方面，可以分为单边规格和双边规格。

单边规格只有规格上限或规格下限，数据越接近上限或下限越好；双边规格有上下限与中心值，数据越接近中心值越好。

其中，USL代表规格上限，LSL代表规格下限，C代表规格中心。

制程准确度Ca用于衡量“实际平均值”与“规格中心值”的一致性。

对于单边规格，不存在规格中心，因此也就不存在Ca；对于双边规格，Ca的等级评定和处理原则与Cp类似。

制程精密度Cp衡量的是“规格公差宽度”与“制程变异宽度”之比例。

对于只有规格上限和规格中心的规格、只有规格下限和规格中心的规格以及双边规格，Cp的等级评定和处理原则也有所不同。

总之，Cpk是一个非常重要的制程能力指数，可以帮助企业量化制程水平，进而采取相应的措施来提升制程能力。

如果需要计算Cpk值，可以使用免费的CPK计算工具。

cpk中的ca计算公式及解释CPK 中的 CA 计算公式及解释在统计质量控制领域中，过程能力指数（CPK）是用于衡量一个过程的稳定性和能力的指标。

CPK 主要通过计算过程的容忍度与可变性之间的差异来评估。

在 CPK 中，CA（Capability Analysis）是计算过程能力的一种常用方法。

CA 计算公式如下：CA = (USL - LS) / (6σ)其中，USL 代表规格上限（Upper Specification Limit）LS 代表规格下限（Lower Specification Limit）σ 代表过程的标准差（Standard Deviation）解释：1. 规格上限（USL）和规格下限（LS）是定义了产品、过程或服务所需的质量特征或性能的上限和下限。

2. 标准差（σ）是用于衡量数据的离散程度，即数据的可变性。

标准差越大，数据的分散程度越高，反之亦然。

3. CA 的计算公式中，将规格的差异（USL - LS）除以过程的可变性（6σ）。

这个比值反映了过程产生不合格产品的潜在能力。

CA 的结果一般是一个小于或等于1的数字。

当 CA 接近于1时，意味着过程能够生产高质量的产品，规格的差异较小。

反之，当 CA 远离1时，说明过程存在较大的变异性，可能产生不合格产品的风险。

通过计算CA，我们可以评估过程的能力，确定其是否能够达到所需质量水平，并采取相应的改进措施来优化过程。

总结：CPK 中的 CA 计算公式为 (USL - LS) / (6σ)，用于评估过程能力。

通过计算这个比值，我们可以判断过程的稳定性和能力，在需要时进行相应的改进和优化，以确保生产高质量的产品。

关于过程能力和过程能力指数的详细解释1、概述前些时间看到不少网友或论坛的朋友一直对Ca、Cp、Cpk、Pp、Ppk产生很多疑问，作为过程质量控制的一部分，我们有必要对它进行全面的了解和精确的计算，以便工作的顺利开展。

Ppk的数量来自长期（一般在3个月或者更长）收集的数据，它可能存在各种波动源，比如：机器老化、员工情绪波动、供应商改变等等。

所以计算Pp和Ppk是有必要的。

2、释义—— Ca偏移修正指数，通常简称“偏移系数”—— Cp无偏移的短期过程能力指数—— Cpk有偏移的短期过程能力指数—— Pp无偏移的长期过程能力指数—— Ppk有偏移的长期过程能力指数3、Ca的计算——Ca值是衡量过程平均值与规格中心值（公差中心值）的一致性，如果Ca越大，标明过程平均值偏离规格中心值越大，过程能力越差；——公式 Ca＝｜x¯-μ｜/(T/2)（x¯表示样本均值，μ规格中心值，T表示公差值）——Ca也是常用的k，k＝ε/（T/2）＝2ε/T；ε＝｜M－x¯｜，M＝（T U＋T L）/24、Cp的计算，σ≈σ^ST ＝R¯/d2＝S¯/ C4——Cp值是衡量过程满足产品品质标准（规规公差）的程度，Cp值越大，表示过程变异越小，过程能力越差；——公式Cp＝T/6σ＝（T U－T L）/6σ≈（T U－T L）/6s（T U公差上限，T L公差下限，σ群体标准差，s样本标准差）；——公式σ＝R¯/d2≈s（R¯表示级差平均值，d2是系数，可以通过查表得知）——群体标准差σ，样本标准差s的换算公式σ＝S/ C4C系数5、Cpk的计算，σ≈σ^ST ＝R¯/d2＝S¯/ C4——Cpk值是分布中心与公差中心不重合情况下的过程能力指数；——公式Cpk＝（1－Ca）Cp＝（1－k）Cp；——当品质规格只有上限单侧公差时：Cpu＝（T U－x¯）/3σ——当品质规格只有下限单侧公差时：Cpl＝（x¯－T L）/3σ6、Pp的计算，σ≈σ^LT＝S——Pp计算方式和Cp计算方式一样，唯一不同的是σ计算公式不一样。

cpk里面的ca标准-回复CPK（Capability Process Index，过程能力指数）是一种统计指标，用于衡量生产过程的稳定性和可控性。

在CPK指数中，CA（Capability Analysis，能力分析）是一种常见的标准，用于确定一个过程是否达到客户要求的水平。

本文将详细介绍CPK指数中的CA标准，并逐步回答与此相关的问题。

一、CPK指数CPK指数是一种通过统计数据来判断一个过程的输出是否满足要求的指标。

它综合考虑了过程的中心位置和过程的离散度，从而判断过程的可控性和稳定性。

CPK指数可以帮助企业评估生产过程的质量水平，进而采取适当的改进措施。

二、CA标准CA标准是CPK指数中常用的一种能力分析方法。

它主要包括以下几个方面：1. 确定产品的规格要求：首先，需要明确定义产品的各种规格要求，比如尺寸、重量、颜色等。

这些规格要求是衡量产品质量的关键指标。

2. 收集数据：收集关于产品规格要求的样本数据。

通常，需要收集的数据应该具有代表性，来自于生产过程的不同阶段和不同批次。

3. 计算过程能力指数：使用收集到的数据，计算过程的CPK指数。

CPK 指数的计算需要考虑过程的均值、标准差以及规格范围。

根据公式：CPK = min[(USL-均值)/(3σ), (均值-LSL)/(3σ)]，其中USL表示规格上限，LSL表示规格下限，σ表示标准差。

4. 判断产品的合格性：根据计算得到的CPK指数，判断产品的合格性。

通常情况下，CPK指数大于1.33表示过程达到了一定的能力水平，可以生产合格产品。

5. 分析改进措施：如果CPK指数低于1.33，说明产品生产过程存在缺陷，需要采取相应的改进措施。

可以通过对数据进行分析，找出过程中的瓶颈和问题，进一步改善生产过程，提高产品质量。

三、常见问题解答1. 为什么要使用CPK指数？CPK指数可以帮助企业评估生产过程的质量水平，确定产品是否满足规格要求。

它能够综合考虑过程的中心位置和离散度，提供一个客观的衡量指标，帮助企业改进生产过程，提高产品质量。

cpk ca的计算方法CPK和CA是用于评估过程能力的统计指标，它们可以衡量一个过程的稳定性和一致性。

CPK和CA的计算方法可以帮助我们判断一个过程是否能够满足特定的要求，并且可以帮助我们分析和改善过程中的问题。

CPK是过程能力指数，它可以衡量一个过程的能力是否达到了特定的要求。

CPK的计算方法是通过比较过程的变异性和规范要求的公差来确定的。

CPK的计算方法可以分为三个步骤：首先，我们需要收集一组样本数据，这些数据应该代表过程的整体情况；然后，我们需要计算过程的平均值和标准差；最后，我们可以使用CPK公式来计算CPK值。

CPK的计算公式如下：CPK = min((USL-平均值)/(3*标准差), (平均值-LSL)/(3*标准差))其中，USL是规范上限，LSL是规范下限，平均值是样本数据的平均值，标准差是样本数据的标准差。

通过计算CPK值，我们可以得出以下结论：1. 如果CPK值大于1，表示过程能力良好，能够满足规范要求；2. 如果CPK值小于1，表示过程能力不足，需要改进。

除了CPK，CA也是一个常用的过程能力指数。

CA是过程能力指数的另一种计算方法，它可以衡量过程的性能和稳定性。

CA的计算方法与CPK类似，但是CA不考虑规范上限和下限的影响，而是通过计算过程的标准差来评估过程的能力。

CA的计算公式如下：CA = (规范上限-规范下限)/(6*标准差)通过计算CA值，我们可以得出以下结论：1. 如果CA值大于1，表示过程能力良好，能够满足规范要求；2. 如果CA值小于1，表示过程能力不足，需要改进。

CPK和CA的计算方法可以帮助我们评估和改善过程能力，但是在实际应用中需要注意以下几点：1. 样本数据的选取应该具有代表性，能够反映过程的整体情况；2. 规范上限和下限的确定应该基于产品或服务的实际需求；3. 标准差的计算应该准确无误，可靠性高；4. CPK和CA值的解释需要结合实际情况进行分析和判断，不能仅仅依靠数值大小来评判过程能力。