2019五年级几何等积变形

小学奥数精讲：等积变形求面积“三角形的面积等于底与高的积的一半”这个结论是大家熟知的，据此我们立刻就可以知道： 等底等高的两个三角形面积相等． 这就是说两个三角形的形状可以不同，但只要底与高分别相等，它们的面积就相等，当然这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”．另一类是两个三角形有一条公共的底边，而这条底边上的高相等，即这条底边的所对的顶点在一条与底边平行的直线上，如右图中的三角形A 1BC 与A 2BC 、A 3BC 的面积都相等。

图形割补是求图形面积的重要方法，利用割补可以把—些形状不规则的图形转换成与之面积相等但形状规则的图形，或把不易求面积的图形转换成易求面积的图形．利用添平行线或添垂线的办法，常常是进行面积割补的有效方法，利用等底等高的三角形面积相等这个性质则是面积割补的重要依据，抓住具体的图形的特点进行分析以确定正确的割补方法则是面积割补的关键．进行图形切拼时，应该有意识地进行计算，算好了再动手寻找切拼的方案．不要盲目地乱动手．本讲中．的几个例子都是经过仔细计算才切拼成功的。

例1、已知三角形ABC 的面积为1，BE ＝ 2AB ，BC ＝CD ，求三角形BDE 的面积?例2、如下图，A 为△CDE 的DE 边上中点，BC=31 CD ，若△ABC(阴影部分)面积为5平方厘米，求△ABD 及△ACE 的面积．例3、 2002年在北京召开了国际数学家大会，大会会标如下图所示，它是由四个相同的直角基本概念例题分析三角形拼成(直角边长为2和3)，问：大正方形面积是多少?例4、下图中，三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形，求阴影部分的面积．练习提高1、如图，已知平行四边形ABCD的面积是60平方分米，E、F分别是AB、AD边上的中点，图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米，宽是12厘米，AF=BE，图中阴影部分的面积是多少平方厘米？3、如图，四边形ABCD 是平行四边形，DC ＝CE ，如果△BCE 的面积是15平方厘米，那么梯形ABED 的面积是多少平方厘米？4、正方形ABCD 的边长是12厘米，已知DE 是EC 长度的2倍，三角形DEF 的面积是多少平方厘米？CF 长多少厘米？5、如图，在平行四边形ABCD 中，AE ＝ED ，BF ＝FC ，CG ＝GD ，平行四边形ABCD 的面积是阴影三角形EFG 的多少倍？（4）6、一个长方形被两条直线分成四个长方形，其中三个面积分别是20平方米，25平方米和30平方米，阴影部分的面积是多少平方米？7、如右图，平行四边形ABCD 的面积是240平方厘米，如果平行四边形内任取一点0，连接AO 、BO 、CO 、DO ，三角形AOD 与三角形BOC 的面积和的21，加上三角形AOB 与三角形DOC 的面积和的31，结果是多少?8、图8-17中，三角形ABC的面积是30平方厘米，D是BC的中点，AE的长是ED的2倍，求三角形CDE的面积．9、如图，正方形的边长为10厘米，用一根铁丝弯成直角，把这根铁丝放到正方形上，使直角顶点与正方形的中心O重合，问正方形在直角内部的部分有多大面积？答案：【例题分析】例1． 4例2．三角形ABD=10平方厘米三角形ACE=15平方厘米例3. 13例4. 27【练习提高】1. 22.52. 1203. 454. 三角形DEF=24平方厘米 CF=6厘米5. 4倍6. 37.57. 1008. 59. 25。

等积变形定理及其应用对平面图形的面积，直观上要承认如下的两条性质： 1. 两个图形完全重合，则这两个图形的面积相等。

2. 把一个图形分成有限个小部分，则整个图形的面积等于所有这些小部分面积之和。

这两条性质，是面积割补的理论基础。

定理1.等底等高的两个三角形的面积相等。

推论1.三角形的一条中线平分这个三角形的面积.推论2.梯形中，以腰为一边，第三个顶点为梯形对角线交点的两个三角形面积相等。

反之，共底的两个三角形的面积相等.若第三个顶点落在底边的同侧，则连接第三顶点的直线与底边所在的直线平行.例1. 凸四边形ABCD 的两组对边中点连线EF , GH 相交于O . 求证: 1.2AEOG CFOH ABCD S S S +=证明: 连接OD , OA ，OB ，OC .则 ()12AEOG AOE AOG AOD AOB S S S S S ∆∆∆∆=+=+ ()12CFOH COF COH BOC COD S S S S S ∆∆∆∆=+=+ 所以 AEOG CFOH S S + ()11.22AOD AOB BOC COD ABCD S S S S S ∆∆∆∆=+++= 例2.如图，四边形ABCD 中，E 和F 分别为 对角线BD 和AC 的中点. 过E 、F 的直线交AB 和CD 分别于M 和N .已知△ABN 的面积为25平 方厘米，求△CDM 的面积. 答：25.解：因为E 是BD 的中点，则BMN DMN S S ∆∆=；因为F 是AC 的中点，则AMN CMN S S ∆∆=. 相加即得25.ABN CDM S S ∆∆== 例3. 右图中ABCD 是个直角梯形（90DAB ABC ∠=∠=）. 以AD 为一边向外作长方 形ADEF ，其面积为6.36平方厘米. 连结BE 交AD 于 P ，连结PC . 求图中阴影部分的面积是多少平方厘米？解：连接AE ，BD . 因为AD//BC ，则PDC PDB S S ∆∆=， 又AB//ED ，则EAD EBD S S ∆∆=.所以EPD PDC EPD PDB S S S S S ∆∆∆∆=+=+阴影EBD EAD S S ∆∆==116.36 3.1822ADEF S ==⨯=（平方厘米）. 例4.过梯形ABCD 的顶点A 作平行于腰 DC 的直线交下底BC 于E 点，交BD 于点 F . 已知三角形ABE 的面积等于15，求三角 形BCF 的面积. 答：15.解：因为F 为梯形ABED 对角线 AE 、BD 的交点，所以三角形ABF 的面积=三角形DEF 的面积. 连接DE . 三角形DEF 的面积=三角形CEF 的面积所以，三角形CBF 的面积=三角形ABE 的面积=15.例5. 在平行四边形ABCD 的边AB 和AD 上分 别取点E 和F ，使得线段EF 平行于对角线BD.求证：三角形BCE 与三角形CDF 等积. 证明：△BCE 的面积=△BDE 的面积 =△BDF 的面积=△C DF 的面积例6. 四边形ABCD 中，M 是AD 的中点， N 是BC 的中点.已知.ABNM DCNM S S = 求证：AD//BC .证明：连接AN ，DN .由于MN 为△AND 的一条中线，所以,AMN DMN S S ∆∆=又已知,ABNM DCNM S S = 所以 .ABN DCN S S ∆∆=（等量减等量其差相等）由于△ABN 与△DCN 的底边在一条直线BC 上，且BN=CN ，点A ，D 在BC 同侧，由定理2可得，AD//BC .例7．P 为五边形ABCDE 内一点，,3AB BP AB ⊥=厘米,4BP =厘米.又AE //,BP PD //BE ，ED //BC . 联结.CE 求三角形CDE 的面积.解：由,3,4,AB BP AB BP ⊥==得 ABP ∆面积为6.联结,PE BD ，则 ,ABP EBP EBD CDE S S S S ∆∆∆∆===所以1134 6.22CDE ABP S S AB BP ∆∆==⋅⋅=⨯⨯=答: 6平方厘米.例8. P 为三角形ABC 内一点,过P 作12//A B AB ,1212//,//.B C BC C A AC求证: 三角形111A B C 与三角形222A B C 的 面积相等.（考虑3种不同的证法） 提示: 连接A 1C 2, C 1B 2, B 1A 2.22PA B ∆面积=21PA B ∆面积=11PA B ∆面积同理可得22PA C ∆面积=12PA C ∆面积=11PA C ∆面积； 22PB C ∆面积=21PB C ∆面积=11PB C ∆面积；相加得三角形111A B C 与三角形222A B C 的 面积相等.例9.如图，四边形ABCD 中,对角线,AC BD 相交于E .,.AF CE BG DE ==如果四边形ABCD 的面积等于2009平方厘米，求EFG ∆的面积.提示：连接AG ，利用等积变形定理得EFG ∆的面积为2009平方厘米. 例10.在五边形12345A A A A A 中, 如果 135424153521//,//,//,A A A A A A A A A A A A4132//,A A A A 求证:5243//.A A A A分析：要证5243//.A A A A只需234A A A ∆面积=534A A A ∆面积. 但4132//A A A A ，有234A A A ∆面积=231A A A ∆面积但3521//,A A A A 有231A A A ∆面积=251A A A ∆面积， 又 2415//,A A A A 有251A A A ∆面积=451A A A ∆面积； 注意到1354//,A A A A 所以451A A A ∆面积=534A A A ∆面积. 因此，234A A A ∆面积=534A A A ∆面积，所以5243//.A A A A例11. 已知ABCDEFG 是凸七边形. 证明: 如果//,//,//,AC EF BD FG CE GA//,//DF AB EG BC 和//FA CD ,那么//.GB DE分析:要证//.GB DE 只需证BDG ∆面积=BEG ∆的面积.因为//,BD FG 有BDG ∆面积=FDB ∆的面积; 由//,DF AB 有FDB ∆的面积=ADF ∆的面积; 由//FA CD ,有ADF ∆的面积=ACF ∆的面积; 由//,AC EF 有ACF ∆的面积=ACE ∆的面积; 由//,CE GA ,有ACE ∆的面积=GCE ∆的面积由//EG BC ,有GCE ∆的面积=GBE ∆的面积,因此，BDG ∆面积=GBE ∆的面积.故得证//.GB DE例12. 如图所示，正方形ABCD 的面积为36 cm 2，正方形EFGH 的面积为256 cm 2，三角形ACG 的面积为27 cm 2，则四边形CDHG 的面积为 cm 2.（第17届华杯赛初赛网络版试题）答：77解：由条件知，正方形ABCD 的边长为6cm. 正方形EFGH 的边长为16 cm. 连接EG ，则45,ACE CEG ∠==∠所以AC//EG . 因此ACGE 是梯形， 所以27==∆∆ACG ACE S S .即27=EC ⨯⨯621，所以EC = 9，因此CH =916-=7，因为四边形CDHG 是个梯形， 所以四边形CDHG 的面积 =7727)166(=⨯+（cm 2）. 定理2. 凸四边形ABCD 的对角线AC , BD 相交于O . 则.ABD CBD S AOS CO∆∆=EFAD E F证明: 由共边定理,得AOD AOBCOD COBS S AO k S CO S ∆∆∆∆===, 所以,AOD COD AOB COB S kS S kS ∆∆∆∆== 相加得 ()AOD AOB COD COB S S k S S ∆∆∆∆+=+ 所以.AOD AOB COD COB S S k S S ∆∆∆∆+=+ 即.ABD CBD S AOk S CO∆∆==特别地, 由ABD CBD S S ∆∆=可以得出结论AO=CO .为用面积方法证明线段相等 提供了新思路.例13. 右图中, 正方形ABCD 的面积为840平方厘米，AE =EB ，BF =2FC ，DF 与EC 相交于G . 则四边形AEGD 的面积为 平方厘米.（第17届华杯赛决赛小高网络版试题6）答: 510解. 连结DE , EF , 则△DEC 的面积=420. △EBC 的面积=210 .△EFC 的面积=13⨯△EBC 的面积13=⨯210=70.所以4206701DEC EFC S FG GD S ∆===，所以6.7DG FD = △DGC 的面积=66140120.77DFC S ∆⨯=⨯=所以 四边形AEGD 的面积=四边形AECD 的面积-△DGC 的面积630120510.=-= 例14如图所示，直角三角形ACB 的两条直角边 AC 和BC 的长分别为14 cm 和28 cm ，CA 和 CB 分别绕点A 和B 点旋转 90至DA 和EB . 若DB 和AE 相交于点P ，求三角形P AB 的ABC DEP面积.（第17届华杯赛决赛初一网络版试题12）答：56.解：易知，45,DCA BCE ∠=∠=90,ACB ∠=所以，DCE 是一条直线.延长DA ，EB 相交于H . 则.DH EH ⊥12828421144232ABE ADEAH BES PB DP S AD EH ∆∆⨯⨯====⨯⨯，因此 44.437PB PB DB DP PB ===++而141498.2ADB ADC S S ∆∆⨯=== 所以449856.77PAB DAB S S ∆∆=⨯=⨯=例15．在△ABC 的边AB ，BC 和CA 上分别取点R ，P ，Q ，使得线段AP ，BQ 和CR 相交于一点M .证明：如果,,AMQ AMR BMR BMP CMP CMQ S S S S S S ∆∆∆∆∆∆===和那么M 是△ABC 三条中线的交点.证明：已知条件中给出的面积，我们通过右图中所示的S 1，S 2和S 3来表示. 因为△ARM 和△BRM 高相同， 所以12.S ARS RB = 类似可得13232,2S S AR S S RB +=+ 也就是12S AR S RB ==132322S S S S ++，由此推出 ()()12321322,S S S S S S +=+ ()3120,S S S ⇒-=因为30,S > 所以S 1=S 2，即AR=RB ，也就是CR 是△ABC 的一条中线.同理类似可证AP 和BQ 也是△ABC 的中线.因此M 是△ABC 三条中线的交点.例16. 如图，梯形ABCD 中，过对角线的交点O 引梯形两底的平行线分别交腰AD 、BC 于点M 和N . 求证：OM=ON.解：如图，连接MB ， 有NBD BOC AOD BMD S S S S ∆∆∆∆=== 在四边形MDNB 中， 因为NBD BMD S S ∆∆=，所以ON = OM .（思考：进一步可证2.ADN CBO S S ∆∆=）例17.在凸四边形ABCD 中，延长边AB 到1B ，使1BB AB =；延长BC 到1C ，使1CC BC =；延长CD 到1D ，使1DD CD =；延长DA 到1A ，使.1AA DA =请你证明：四边形1111D C B A 的面积是四边形ABCD 面积的5倍.证明： 由下左图，连接11,,,CA CB AD设12,.ABCACDS s Ss ==则1112,BB C Ss =1122,A DD Ss =所以11BB C S +11122()2A DD ABCD Ss s S =+=……①同理由上右图，连接11,,,C D BA BD 设34,.ABDBCDSs Ss ==则1132,A AB Ss =1142,C CD Ss =所以 11A AB S+11342()2C CD ABCD Ss s S =+=……②① + ②得 11BB C S+11A DD S+11A AB S +114C CD ABCD SS =所以 1111A B C D S =11(BB C S +11A DD S+11A AB S+11)5.C CD ABCD ABCD SS S +=例18． 如图，在直角ABC ∆的两直角边AC 、BC 上分别作正方形ACDE 和 CBFG . 连结AF 、BE 分别交 BC 、AC 于Q ，P . 求证：CP = CQ . 证明：注意AG = AC + CG = D C + CB = BD因为ABC BCE BPD ∆=∆=∆ ABC ACF AQG ∆=∆=∆所以AQG BPD ∆=∆ 即21BD ×CP =21AG ×CQ . 由于AG = BD ，所以CP = CQ.例19. 如右图所示, 四边形ABCD 的面积为6, 点M , N , P , Q 分别为各边的中点. 点O 为ABCD 内的一点. 连接OM 并延长至E 点, 使得2OM ME =, 同样的方式可得点F , G , H . 则四边形EFGH 的面积为 . 答: 27.解. 连接,,,MN NP PQ QM , 因为点,,,M N P Q 分别为四边形ABCD 各边的中点, 所以四边形MNPQ 的面积为四边形ABCD 面积的一半, 即四边形MNPQ 的面积为 3.因为2ME OM =且2NF ON =, 容易得到三角形OEF 的面积是三角OMN 的面积的9倍.同理可得三角形OFG 的面积是三角形ONP 的面 积的9倍；三角形OGH 的 面积是三角形OPQ 的面积 的9倍；三角形OHE 的面积是三角形OQM 的面积的9倍.所以四边形EFGH 的面积是四边形MNPQ 的面积9倍, 即四边形EFGH 的面积为27.例20．如图, 在五边形ABCDE 中, M ，N 分别是AB ，AE 的中点. 四边形AMPN ，△CPM ， △ CPD ，△DPN 的面积分别是9，6，9，6. 求五边形ABCDE 的面积.解：易知30.AMCDN S =连接MN ，设,MNP S x ∆=则:66:9x =推得 4.x =所以94 5.AMN S ∆=-=连接AC ，AD ，分别交MN 于F ，G . 由15//MCD NCD S S MN ∆∆==⇒CD . 在四边形AMCN 中， 51,462AMN CMN S AF FC S ∆∆===+ 同理可证1.2AG DG = 连接DF ，则6915.FCD MCD S S ∆∆==+=由于1,7.52AFD AF S FC ∆=⇒=，22.5.ACD S ∆= 因此3022.57.5.AMC AND AMCDN ACD S S S S ∆∆∆+=-=-= 由于M ，N 分别是AB ，AE 的中点，,,BMC AMC DNE AND S S S S ∆∆∆∆== 7.5.BMC DNE AMC AND S S S S ∆∆∆∆+=+=所以 ABCDE AMCDN BMC DNE S S S S ∆∆=++=30 +7.5 = 37.5. 例21. 平行四边形ABCD 的边AD 上 任取一点N ，过N 作平行于对角线AC 、 BD 的直线分别交边AB 、CD 于点M 和K.证明：三角形NMB 与NKC 等积.11。

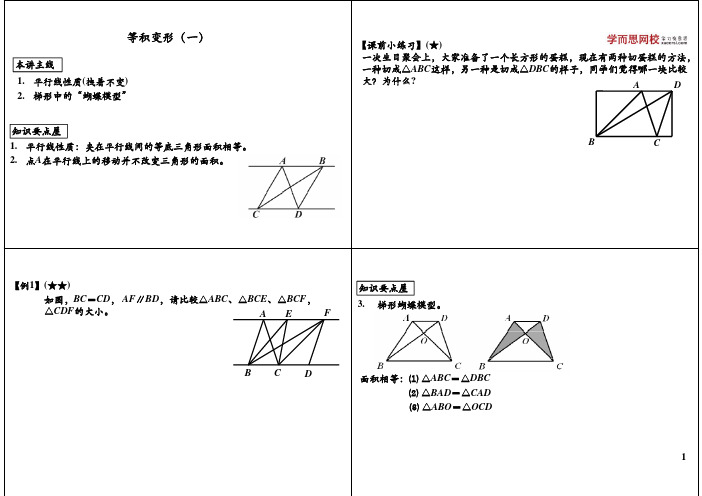
等积变形（一）本讲主线 1. 平行线性质(拽着不变) 1 2. 梯形中的“蝴蝶模型” 知识要点屋 1. 平行线性质：夹在平行线间的等底三角形面积相等。

2. 点A在平行线 在平行线上的移动并不改变三角形的面积。

移 并 变 角形【课前小练习】(★) 一次生日聚会上，大家准备了一个长方形的蛋糕，现在有两种切蛋糕的方法， 次生日聚会上 大家准备了 个长方形的蛋糕 现在有两种切蛋糕的方法 一种切成△ABC这样，另一种是切成△DBC的样子，同学们觉得哪一块比较 大？为什么? A DBC【例1】(★★) 图，BC＝CD， AF∥BD，请 ，请比较△ 较 ABC、△BCE、△BCF， 如图， △CDF的大小。

F A E知识要点屋 3 3. 梯形蝴蝶模型 梯形蝴蝶模型。

BCD面积相等：⑴ △ABC＝△DBC ⑵ △BAD＝△CAD ⑶ △ABO＝△OCD1【例2】(★★★) 如图，在梯形ABCD中，共有八个三角形，其中面积相等的三角形共 有哪几对？【例3】(★★★★) 如图，在平行四边形ABCD中，直线CF交AB于E，交DA延长线于F， 若S△ADE＝1，求△BEF的面积。

知识要点屋 3 一半模型。

3. 半模型【例4】(★★★) 如图所示，四边形ABCD与AEGF都是平行四边形，请你证明它们的面 积相等。

G A D F阴影面积＝长方形÷2BEC2【例5】(★★★★) 正方形ABCD和正方形CEFG，且正方形ABCD边长为12厘米，则图中 阴影面积为多少平方厘米？【例6】(★★★★☆) 如图，过平行四边形ABCD定点D作直线交BC于点E，交AB延长线于F 点，已知△AEF的面积为10平方厘米，求△BFC的面积。

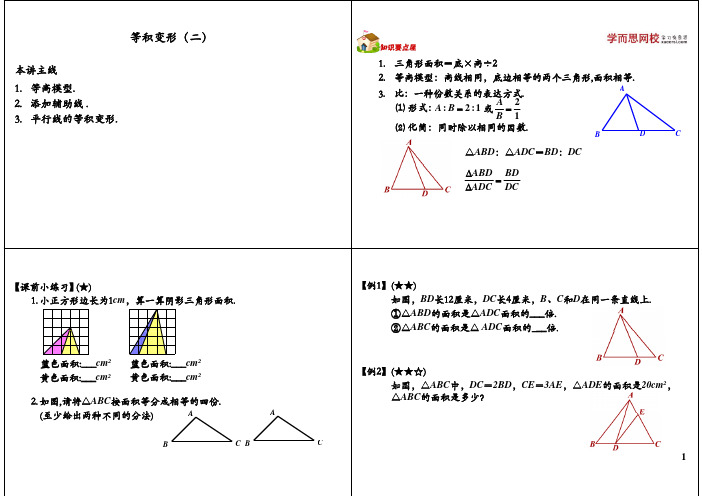
A B F CDE知识大总结 1. 平行线性质：夹在平行线间的等底三角形面积相等。

平行线性质 夹在平行线间的等底 角形面积相等。

2. 梯形蝴蝶模型：任意一个梯形中，都可以找到三对面积相等的三角形。

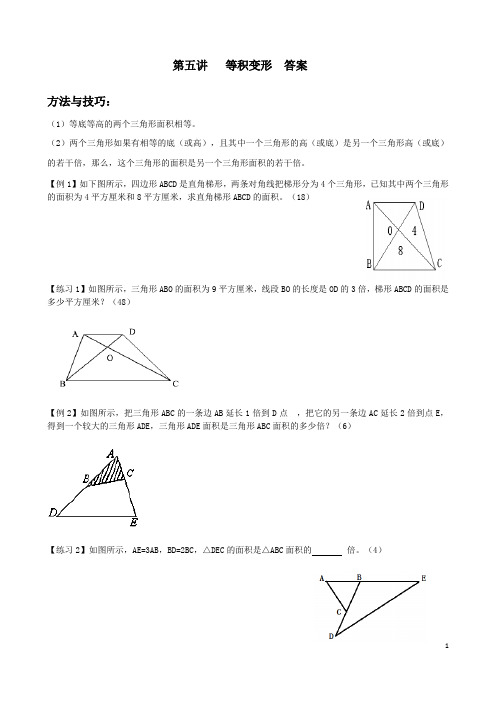
第五讲等积变形答案方法与技巧：（1）等底等高的两个三角形面积相等。

（2）两个三角形如果有相等的底（或高），且其中一个三角形的高（或底）是另一个三角形高（或底）的若干倍，那么，这个三角形的面积是另一个三角形面积的若干倍。

【例1】如下图所示，四边形ABCD是直角梯形，两条对角线把梯形分为4个三角形，已知其中两个三角形的面积为4平方厘米和8平方厘米，求直角梯形ABCD的面积。

（18）【练习1】如图所示，三角形ABO的面积为9平方厘米，线段BO的长度是OD的3倍，梯形ABCD的面积是多少平方厘米？（48）【例2】如图所示，把三角形ABC的一条边AB延长1倍到D点，把它的另一条边AC延长2倍到点E，得到一个较大的三角形ADE，三角形ADE面积是三角形ABC面积的多少倍？（6）【练习2】如图所示，AE=3AB，BD=2BC，△DEC的面积是△ABC面积的倍。

（4）【例3】已知三角形ABC面积为56平方厘米，是平行四边形DEFC的2倍，则阴影部分的面积是多少平方厘米？（14）【例4】如图所示，矩形ABCD的面积为24平方厘米，三角形ADM与三角形BCN的面积和为7.8平方厘米，则四边形PMON的面积是多少平方厘米？（1.8）【例5】如图所示，点M、N、P、Q分别在平行四边形ABCD的边AB、BC、CD、DA上，且PE//GM//CB，HN//QF//AB。

若平行四边形ABCD的面积为600平方厘米、阴影部分的面积为80平方厘米。

请问四边形MNPQ的面积为多少平方厘米？（340）【例6】如图所示，在正方形ABCD的BC边上取一动点E，以DE为边作矩形DEFG，且FG边通过点A。

在点E从点B移动到点C过程中，矩形DEFG的面积（）（E）（A）一直变大。

（B）一直变小。

（C）先变小后变大。

（D）先变大后变小。

（E）保持不变。

【练习1】如左下图，△ABC中，D、E分别为边BC、AB的中点。

若图中阴影部分面积为1，则△ABC的面积为多少？（4）【练习2】如右上图所示，图中阴影部分的面积为多少平方厘米？（24）【练习3】如图，六角形的6个顶点恰好是一个正六边形的6个顶点。

学生课程讲义
两个平面图形面积相等,称为这两个图形等积.解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积问题.其中三角形的等积变形的技巧是各种
等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则,并由此衍生出因题而宜的种种精巧的等积变形的技巧。

【例1】计算：
如图，5-1，ABCD 是直角梯形，两条对角线把梯形分为4个三角形，已知其中两个三角形的面积为3平方厘米和6平方厘米，求直角梯形ABCD 的面积。

【例2】
其中A、B、C都是大于0且互不相同的自然数，则（A+B）÷C＝。

等积变形篇丁志浩物体的形状虽然改变了，但是其面积或体积仍然保持不变．这类问题我们可以称为等积变形问题．在等积变形问题中，变化前后的体积或面积相等，往往是列方程所需的重要的相等关系．1.面积不变问题例1将图（1）三角形纸片沿虚线叠成图（2），原三角形图（1）的面积是图（2）（粗实线图形）面积的1.5倍，已知图（2）中阴影部分的面积之和为1，求重叠部分的面积.解析：首先要看清题意，其中图（2）中粗实线图形面积就是图（3）中三个角上的小三角形面积和重叠部分面积的总和，这个题目中的等量关系我们可以从图中不难看出，就是整个三角形的面积是三个角上小三角形(从图（3）中看)面积和重叠（从图（2）中看）部分面积的总和的1.5倍.如果设重叠部分面积为x，将折叠还原后，则原三角形的面积是（2x+1），图（2）中粗实线部分面积是（x+1）,等量关系为：原三角形的面积=1.5粗实线部分面积解：设重叠部分面积为x.根据题意，得1.5(x+1)=2x+1.解得x=1.所以重叠部分的面积为1.例2如图2，“回”字形的道路宽为1米，整个“回”字形的长为8米，宽为7米，一个人从入口点A沿着道路走到终点B，他共走了多少米？分析：如果我们直接解这个问题，这里有重复部分，是个十分麻烦问题，现在需要对这个问题转化，可以看作用一米宽的拖把把这块区域托一遍，我们以走直线方式拖地，那么拖把走过区域是长方形，长方形的宽是一定的，是一米.而长方形的长就是拖把走过路程.长方形的面积就等于回字形面积，直接就可以算出拖把走过的路程是56米.而这正是人要走的路程.这时候我们可以看到这和拖把是否走直线没有关系了，只要拖把的宽度一定，它走过的路程就定下来，就是56米.我们也可以这样来看：所有小路连在一起可以组成一个宽1米的长长的长方形，因为长方形场地“充满”了小路，所以小路的面积等于长方形场地的面积．解：设小路的总长度为x米.根据题意，得x×1=8×7．解得x=56．所以从入口A处走到终点B，至少要走56米．2.体积不变问题例3 用直径为90mm的圆柱形玻璃杯（已装满水，且水足够多）向一个内底面积为131× 131mm2，内高为81mm的长方体铁盒倒水，当铁盒装满水时，玻璃杯中水的高度下降了多少？（结果保留π）分析：因为铁盒里水是满的，所以水的体积就等于铁盒的容积.根据长方体的体积公式可以计算出水的体积是131×131×81 mm3 ，圆柱形玻璃杯中减少的的体积为圆柱的底面积乘以水下降的高度.显然玻璃杯里倒掉的水的体积和长方体铁盒里所装的水的体积相等，所以等量关系为：玻璃杯里倒掉的水的体积=长方体铁盒的容积.解：设玻璃杯中水的高度下降了xmm.根据题意，得π·(90÷2)2x=131×131×81.解得π44.686x. 经检验，它符合题意．所以玻璃杯中水的高度下降了π44.686mm.例4将一个长、宽、高分别为15厘米、12厘米和8厘米的长方体钢块锻造成一个底面（正方形）边长为12厘米的长方体零件钢坯，试问是锻造前的长方体钢块表面积大还是锻造后的长方体零件钢坯表面积大？请你进行比较．分析：锻造前长方体钢块的体积为15×12×8cm3，锻造后长方体零件钢坯体积为12×12×它的高cm3.虽然钢块的形状发生了变化，但是钢块的体积没有变化．因此可得长方钢块体的体积=长方体零件钢坯体积,如果设长方体零件钢坯高为x厘米,得15×12×8=12×12×x.显然可以算出它的高=10厘米,但问题到此并没有结束,最终要比较它们的表面积的. 锻造前长方体钢块的表面积为为2×(12×15+15×8+12×8)平方厘米,锻造后长方体零件钢坯的表面积是2×(12×12+12×10+12×10)平方厘米.解：设锻造后的长方体零件钢坯的高为x厘米.根据题意，得5×12×8=12×12×x．解得10x=．所以锻造后的长方体零件钢坯表面积为：2(121212101210)768⨯⨯+⨯+⨯=（平方厘米）．而锻造前的长方体钢块表面积为：2(1512158128)792⨯⨯+⨯+⨯=（平方厘米）．所以锻造前的长方体钢块表面积比锻造后的长方体零件钢坯表面积大．例5 一种圆筒状包装的，如图3所示，其规格为“20cm×60m”，经测量这筒保鲜膜的内径、外径的长分别是3.2cm、4.0cm，则这种保鲜膜的厚度约为多少厘米？（π取3.14，结果保留两位有效数字）分析：当我们把圆筒状包装的保鲜膜展开时原来的形状可以看成长方体，根据长方体的体积公式可以计算出此时的体积为20ⅹ6000ⅹ保鲜膜的厚度，需要说明的是20 cm指展开后鲜膜的宽，也是展开前圆筒状包装的高，60 m是保鲜膜展开后的长度(单位要统一).圆筒状时可以看成圆柱体，我们要注意这个圆柱是空心的，计算时不能忘了减去空心部分．展开前后形状虽然改变了，但体积不变.即圆筒状包装体积=长方体的体积.解：设这种保鲜膜的厚度为x cm.根据题意，得223.2202060002x ⎡⎤4⎛⎫⎛⎫π-=⨯⎢⎥⎪ ⎪2⎝⎭⎝⎭⎢⎥⎣⎦．解得0.00075x≈．所以这种保鲜膜的厚度约为0.00075cm．例6 一张桌子有一个桌面和四条桌腿，做一张桌面需要木材0.03m3，做一条桌腿需要木材0.002m3，现做一批这样的桌子，恰好用去木材3.8m3，共做了多少张桌子？分析：解决这个问题关键是找出一个能表示实际问题全部意义的相等关系，我们要注意的是：一张桌子有一个桌面和四条腿，那么整张桌子所需的木材的体积是四条腿的和一个桌面的，如果设共做桌子X张，我们就容易用X表示出做桌腿所需木材的体积是4ⅹ0.002X m3 ，做桌面所需的木材的体积是0.03X m3 .因此这个问题中就有这样的相等关系：做桌面所需木材的体积+做桌腿所需木材的体积=3.8m3解：设共做了x张桌子.根据题意,得0.003x+4×0.002x=3.8.解得x=100.所以共做100张桌子.同步练习1.现有直径为0.8米的圆柱形钢坯30米，可足够锻造直径为0.4米，长为3米的圆柱形机轴多少根？2．德鑫轧钢厂要把一种底面直径6厘米，长1米的圆柱形钢锭，轧制成长4.5米，外径3厘米的无缝钢管，如果不计加工过程中的损耗，则这种无缝钢管的内径是（）A． 0.25厘米 B． 2厘米C．1 厘米 D． 0.5厘米3．用直径为90 mm的圆柱形玻璃杯（已装满水）向一个由底面积为125×125 mm2内高为81mm的长方体铁盒倒水时，当倒满铁盒时玻璃杯中的水的高度下降多少？（结果保留整数π≈3.14）4．圆柱（1）的底面直径为10厘米，高为18厘米；圆柱（2）的底面直径为8厘米.已知圆柱（2）的体积是圆柱（1）的体积的1.5倍，求圆柱（2）的高.5．将内径为200毫米的圆柱形水桶中的满桶水倒入一个内部长、宽、高分别为300毫米、300毫米、80毫米的长方体铁盒，正好倒满，求圆柱形水桶的水高（精确到1毫米，≈3.14）.6.一张圆桌由一个桌面和四条腿组成，如果1m三次方，木料可制作圆桌的桌面50个，或制桌腿300条，现有5m三次方，木料，请你设计一下，用多少木料.7.如图是两个圆柱体的容器，它们的半径分别是4cm和8cm，高分别为16cm和10cm，先在第一个容器中倒满水，然后将其全部倒入第二个容器中.（1）倒完后，第二个容器水面的高度是多少？(2)如右图把容器1口朝上插入容器2水位又升高多少？容器2同步练习1.现有直径为0.8米的圆柱形钢坯30米，可足够锻造直径为0.4米，长为3米的圆柱形机轴多少根？1、分析：变形前钢坯的体积等于变形后所有圆柱形机轴的总体积2．德鑫轧钢厂要把一种底面直径6厘米，长1米的圆柱形钢锭，轧制成长4.5米，外径3厘米的无缝钢管，如果不计加工过程中的损耗，则这种无缝钢管的内径是（）A． 0.25厘米 B． 2厘米C．1 厘米 D． 0.5厘米3．用直径为90 mm的圆柱形玻璃杯（已装满水）向一个由底面积为125×125 mm2内高为81mm的长方体铁盒倒水时，玻璃杯中的水的高度下降多少？（结果保留整数π≈3.14）4．圆柱（1）的底面直径为10厘米，高为18厘米；圆柱（2）的底面直径为8厘米.已知圆柱（2）的体积是圆柱（1）的体积的1.5倍，求圆柱（2）的高.5．将内径为200毫米的圆柱形水桶中的满桶水倒入一个内部长、宽、高分别为300毫米、300毫米、80毫米的长方体铁盒，正好倒满，求圆柱形水桶的水高（精确到1毫米，≈3.14）.6.一张圆桌由一个桌面和四条腿组成，如果1m三次方，木料可制作圆桌的桌面50个，或制桌腿300条，现有5m三次方，木料，请你设计一下，用多少木料.7.如图是两个圆柱体的容器，它们的半径分别是4cm和8cm，高分别为16cm和10cm，先在第一个容器中倒满水，然后将其全部倒入第二个容器中.（1）倒完后，第二个容器水面的高度是多少？(2)如右图把容器1口朝上插入容器2水位又升高多少？容器2。

年 级授课日期 授课主题 第5讲——等积变形教学内容i.检测定位两个平面图形面积相等，称为这两个图形等积.解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积.其中三角形的等积变形的技巧是各种等积变形的核心，都要运用到“等（同）底、等（同）高的两个三角形面积相等”这个基本规则，并由此衍生出因题而宜的种种精巧的等积变形的技巧.【例1】如图5-1，ABCD 是直角梯形，两条对角线把梯形分为4个三角形.已知其中两个三角形的面积为3平方厘米和6平方厘米，求直角梯形ABCD 的面积.分析与解 因为三角形ADC 和三角形ADB 同底等高，所以ADB ADC S S ∆∆=，又三角形AOD 是公共部分，可知).(3平方厘米==∆∆COD AOB S S在三角形BOC 与三角形DOC 中，BO 、OD 边上的高相等，6是3的2倍，可知OD BO 2=，得AOD AOB S S ∆∆=2，这样).(5.123平方厘米=÷=∆AOD S 因此，).(5.13)36(3336平方厘米梯形=÷÷+++=ABCD S随堂练习1如图5-2，三角形ABO 的面积为9平方厘米，线段BO 的长度是线段OD 的3倍，梯形ABCD 的面积是多少平方厘米？【例2】如图5-3，把三角形ABC 的一条边AB 延长1倍到D ，把它的另一边AC 延长2倍到E ，得到一个较大的三角形ADE ，三角形ADE 的面积是三角形ABC 面积的多少倍？分析与解 如图5-4，连结BE ，因为AC CE 2=，所以ABC BCE S S ∆∆=2，即ABC ABE S S ∆∆=3.又因为BD AB =，则BDE ABE S S ∆∆=，ABC ADE S S ∆∆=6.随堂练习2如图5-5，DBE BC BD AB AE ∆==,2,3面积是ABC ∆面积的________倍.【例3】如图5-6，已知三角形ABC 的面积为56平方厘米，是平行四边形DEFC 的2倍，阴影部分的面积是多少平方厘米？分析与解 如图5-7，连结EC .EC 为平行四边形DEFC 的对角线.平行四边形DEFC 的面积是（平方厘米）28256=÷，由平行四边形的性质有.2S DEC ÷=∆DEFC S 平行四边形在ED CED AED 中，与∆∆为公共底，,AC DE 平行于则 ED 边上的高相等，因此.DEC AED S S ∆∆=).(1422562平方厘米=÷÷=÷==∆∆DEFC DEC AED S S S随堂练习3如图5-8，ABC ∆的面积等于24平方厘米，M 为AB 中点，E 为AM 上任意一点，MD 与EC 平行.求EBD ∆的面积.【例4】如图5-9所示，矩形ABCD 的面积为24平方厘米，三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则四边形PMON 的面积是__________平方厘米.分析与解 三角形AOD 与三角形BOC 的面积之和为矩形ABCD 面积的一半，先求出三角形AOM 和三角形NOB 的面积之和，由三角形ABP 的面积减去三角形AOB 的面积，再减去三角形AOM 和三角形NOB 的面积和，就可求出四边形PMON 的面积了.).(2.48.7224平方厘米=-÷=+∆∆NOB AOM S S).(8.14242.4224平方厘米四边形=÷--÷=PMON S说明 本题说求的阴影部分面积看似无从下手，实质上只要我们理清楚解题的思路分步考虑，脚踏实地地去做，求出本题的答案是不难的.随堂练习4如图5-10，平行四边形ABCD 中DF BF 2=，.的中点是BC E 平方厘米，8=∆BEF S 求平行四边形ABCD 的面积.【例5】如图5-11，梯形ABCD 的面积是45平方厘米，高是6厘米，BC AD //.三角形AED 的面积是5平方厘米，厘米10=BC ，求三角形BCE 的面积.分析与解 由已知量，可先求出上底AD ，进而求出三角形ABD （或ACD ）面积及三角形ABE 面积，利用等积变换可知三角形ABE 与三角形CDE 等积.最后得到三角形BCE 的面积.由梯形的面积公式得 6102145⨯+⨯=）（AD ， 解得厘米5=AD ，进而 )(155621平方厘米=⨯⨯=∆ABD S . 由等积变形知 ACD ABD S S ∆∆=，从而 )(10515平方厘米=-==∆∆CDE ABE S S .所以 )(20210545平方厘米=⨯--=∆BCE S .【例6】如图5-12，已知长方形宽是长的32，平方厘米14=∆ABC S ，AD AC 31=，EF DE =.求阴影部分的面积.分析与解 连结BD ，因为AD AC 31=，所以，)(421433平方厘米=⨯=⨯=∆∆ABC ABD S S ， 从而)(84422平方厘米长方形=⨯=ABFD S .又因为EF DE =，所以 )(21844141平方厘米长方形=⨯==∆ABFD BFE S S ， 从而 )(49211484平方厘米长方形阴影面积=--=--=∆∆BFE ABC ABFD S S S S .随堂练习5如图5-13，梯形ABCD 中，BC AD //，对角线交于O ，三角形AOD 面积为20，三角形ABO 面积为30.求梯形ABCD 的面积.（单位：平方厘米）读一读不要轻易放弃题目 平面上有7个点，任意三点不在同一直线上.以上这7个点作为定点作三角形，使任意两个三角形至多只有一个公共顶点.问最多可以作出多少个满足上述条件的三角形？我在纸上画了很多草图，费尽心思，想得到合乎要求的7个三角形，但没有结果.只好向单墫请教，他很快就给出了解答，非常精彩.在他的解答中有一句话使我心头一震：“在构造这7个三角形时，每一个点恰好用了3次”.事后，我又回顾了自己的思路，有两张草图印象很深.第一张是开始时的草图（图1），这是第一个念头，只能作出3个符合要求的三角形.于是想在此图基础上连线增加符合要求的三角形，虽然有所改进，但毫无章法，很快就放弃了.为了改进作图，我先将7个点放在圆上，可保证无3个点共线，两两连线，得到以给定7个点为顶点的所有三角形（图2），我知道要求的7个三角形必在其中.但要把他们找出来，并加以说明又很困难.然而当单老师的信息“每个点恰用3次”出现时，我的第1个年头立刻浮现在眼前，图中的“1”不正好直观地被用了3次吗？如果对1进行轮换，用2、3、4、5、6、7替换1，就可产生2173=⨯个符合要求的三角形，而因为每个点恰好用了3次，因此，合乎题目要求的三角形正好是7个，这7个三角形的3个顶点分别为（1,2,3），（3,4,5），（5,6,1），（1,7,4），（3,7,6），（5,7,2），（2,4,6）.上面的想法几乎在一瞬间完成，再去复查2,7个三角形很容易找出来了.单老师在谈解题思路是常说，做不出来不要紧，很多想法虽然没有解决全部问题，但其中或解决了部分问题，或隐含着解决问题的合理成分.关键是要会总结，碰了钉子不要紧，不一定全部放弃你原来的想法.ii.针对培养1.如图，ABC ∆中，D 、E 分别为各边重点.若阴影部分面积为1，则ABC ∆的面积为_________.2.如图，同种阴影部分的面积为__________平方厘米.3.如图，梯形的下底长为10厘米，高为6厘米，阴影部分的面积是________平方厘米.4.如图，平行四边形中，A 、M 、N 分别为对应线段的中点，且阴影部分面积为15平方厘米，则大平行四边形的面积是__________平方厘米.5.如图，将ABC ∆的AB 边延长1倍，将BC 边延长2倍，得ADE ∆，则ADE ∆的面积是ABC ∆面积的________倍.6.如图，,4,3CD AC BE BC ==则ABC ∆的面积是DEA ∆面积的________倍.7.如图，求平行四边形中阴影部分面积.（单位：厘米）8.如图，ABC ∆中，.32==BD AD ，四边形DBEF 的面积等于ABE ∆的面积.若ABC ∆的面积等于10，则四边形DBEF 的面积是多少？9.如图，梯形ABCD 中，BC AD //，ABE ∆的面积为30平方厘米，.2AE EC =求梯形ABCD 的面积.10.如图，ABC ∆的面积是72平方厘米，D 是BC 的中点，.2,3EF FD AE BE ==求三角形AFD 面积.11.如图，ABC ∆的面积为14平方厘米，.,3ED AE DB DC ==求阴影部分面积.12.如图，长方形ABCD 中，,2,,GF EG FC DF ED AE ===且长方形的长和宽分别是10厘米、6厘米.则BFG ∆的面积是多少？。

等积变形定理及其应用对平面图形的面积，直观上要承认如下的两条性质： 1. 两个图形完全重合，则这两个图形的面积相等。

2. 把一个图形分成有限个小部分，则整个图形的面积等于所有这些小部分面积之和。

这两条性质，是面积割补的理论基础。

定理1.等底等高的两个三角形的面积相等。

推论1.三角形的一条中线平分这个三角形的面积.推论2.梯形中，以腰为一边，第三个顶点为梯形对角线交点的两个三角形面积相等。

反之，共底的两个三角形的面积相等.若第三个顶点落在底边的同侧，则连接第三顶点的直线与底边所在的直线平行.例1. 凸四边形ABCD 的两组对边中点连线EF , GH 相交于O . 求证: 1.2AEOG CFOH ABCD S S S +=证明: 连接OD , OA ，OB ，OC .则 ()12AEOG AOE AOG AOD AOB S S S S S ∆∆∆∆=+=+ ()12CFOH COF COH BOC COD S S S S S ∆∆∆∆=+=+ 所以 AEOG CFOH S S + ()11.22AOD AOB BOC COD ABCD S S S S S ∆∆∆∆=+++= 例2.如图，四边形ABCD 中，E 和F 分别为 对角线BD 和AC 的中点. 过E 、F 的直线交AB 和CD 分别于M 和N .已知△ABN 的面积为25平 方厘米，求△CDM 的面积. 答：25.解：因为E 是BD 的中点，则BMN DMN S S ∆∆=；因为F 是AC 的中点，则AMN CMN S S ∆∆=. 相加即得25.ABN CDM S S ∆∆== 例3. 右图中ABCD 是个直角梯形（90DAB ABC ∠=∠=）. 以AD 为一边向外作长方 形ADEF ，其面积为6.36平方厘米. 连结BE 交AD 于 P ，连结PC . 求图中阴影部分的面积是多少平方厘米？解：连接AE ，BD . 因为AD//BC ，则PDC PDB S S ∆∆=， 又AB//ED ，则EAD EBD S S ∆∆=.所以EPD PDC EPD PDB S S S S S ∆∆∆∆=+=+阴影EBD EAD S S ∆∆==116.36 3.1822ADEF S ==⨯=（平方厘米）. 例4.过梯形ABCD 的顶点A 作平行于腰 DC 的直线交下底BC 于E 点，交BD 于点 F . 已知三角形ABE 的面积等于15，求三角 形BCF 的面积. 答：15.解：因为F 为梯形ABED 对角线 AE 、BD 的交点，所以三角形ABF 的面积=三角形DEF 的面积. 连接DE . 三角形DEF 的面积=三角形CEF 的面积所以，三角形CBF 的面积=三角形ABE 的面积=15.例5. 在平行四边形ABCD 的边AB 和AD 上分 别取点E 和F ，使得线段EF 平行于对角线BD.求证：三角形BCE 与三角形CDF 等积. 证明：△BCE 的面积=△BDE 的面积 =△BDF 的面积=△C DF 的面积例6. 四边形ABCD 中，M 是AD 的中点， N 是BC 的中点.已知.ABNM DCNM S S = 求证：AD//BC .证明：连接AN ，DN .由于MN 为△AND 的一条中线，所以,AMN DMN S S ∆∆=又已知,ABNM DCNM S S = 所以 .ABN DCN S S ∆∆=（等量减等量其差相等）由于△ABN 与△DCN 的底边在一条直线BC 上，且BN=CN ，点A ，D 在BC 同侧，由定理2可得，AD//BC .例7．P 为五边形ABCDE 内一点，,3AB BP AB ⊥=厘米,4BP =厘米.又AE //,BP PD //BE ，ED //BC . 联结.CE 求三角形CDE 的面积.解：由,3,4,AB BP AB BP ⊥==得 ABP ∆面积为6.联结,PE BD ，则 ,ABP EBP EBD CDE S S S S ∆∆∆∆===所以1134 6.22CDE ABP S S AB BP ∆∆==⋅⋅=⨯⨯=答: 6平方厘米.例8. P 为三角形ABC 内一点,过P 作12//A B AB ,1212//,//.B C BC C A AC求证: 三角形111A B C 与三角形222A B C 的 面积相等.（考虑3种不同的证法） 提示: 连接A 1C 2, C 1B 2, B 1A 2.22PA B ∆面积=21PA B ∆面积=11PA B ∆面积同理可得22PA C ∆面积=12PA C ∆面积=11PA C ∆面积； 22PB C ∆面积=21PB C ∆面积=11PB C ∆面积；相加得三角形111A B C 与三角形222A B C 的 面积相等.例9.如图，四边形ABCD 中,对角线,AC BD 相交于E .,.AF CE BG DE ==如果四边形ABCD 的面积等于2009平方厘米，求EFG ∆的面积.提示：连接AG ，利用等积变形定理得EFG ∆的面积为2009平方厘米. 例10.在五边形12345A A A A A 中, 如果 135424153521//,//,//,A A A A A A A A A A A A4132//,A A A A 求证:5243//.A A A A分析：要证5243//.A A A A只需234A A A ∆面积=534A A A ∆面积. 但4132//A A A A ，有234A A A ∆面积=231A A A ∆面积但3521//,A A A A 有231A A A ∆面积=251A A A ∆面积， 又 2415//,A A A A 有251A A A ∆面积=451A A A ∆面积； 注意到1354//,A A A A 所以451A A A ∆面积=534A A A ∆面积. 因此，234A A A ∆面积=534A A A ∆面积，所以5243//.A A A A例11. 已知ABCDEFG 是凸七边形. 证明: 如果//,//,//,AC EF BD FG CE GA//,//DF AB EG BC 和//FA CD ,那么//.GB DE分析:要证//.GB DE 只需证BDG ∆面积=BEG ∆的面积.因为//,BD FG 有BDG ∆面积=FDB ∆的面积; 由//,DF AB 有FDB ∆的面积=ADF ∆的面积; 由//FA CD ,有ADF ∆的面积=ACF ∆的面积; 由//,AC EF 有ACF ∆的面积=ACE ∆的面积; 由//,CE GA ,有ACE ∆的面积=GCE ∆的面积由//EG BC ,有GCE ∆的面积=GBE ∆的面积,因此，BDG ∆面积=GBE ∆的面积.故得证//.GB DE例12. 如图所示，正方形ABCD 的面积为36 cm 2，正方形EFGH 的面积为256 cm 2，三角形ACG 的面积为27 cm 2，则四边形CDHG 的面积为 cm 2.（第17届华杯赛初赛网络版试题）答：77解：由条件知，正方形ABCD 的边长为6cm. 正方形EFGH 的边长为16 cm. 连接EG ，则45,ACE CEG ∠==∠所以AC//EG . 因此ACGE 是梯形， 所以27==∆∆ACG ACE S S .即27=EC ⨯⨯621，所以EC = 9，因此CH =916-=7，因为四边形CDHG 是个梯形， 所以四边形CDHG 的面积 =7727)166(=⨯+（cm 2）. 定理2. 凸四边形ABCD 的对角线AC , BD 相交于O . 则.ABD CBD S AOS CO∆∆=EFAD E F证明: 由共边定理,得AOD AOBCOD COBS S AO k S CO S ∆∆∆∆===, 所以,AOD COD AOB COB S kS S kS ∆∆∆∆== 相加得 ()AOD AOB COD COB S S k S S ∆∆∆∆+=+ 所以.AOD AOB COD COB S S k S S ∆∆∆∆+=+ 即.ABD CBD S AOk S CO∆∆==特别地, 由ABD CBD S S ∆∆=可以得出结论AO=CO .为用面积方法证明线段相等 提供了新思路.例13. 右图中, 正方形ABCD 的面积为840平方厘米，AE =EB ，BF =2FC ，DF 与EC 相交于G . 则四边形AEGD 的面积为 平方厘米.（第17届华杯赛决赛小高网络版试题6）答: 510解. 连结DE , EF , 则△DEC 的面积=420. △EBC 的面积=210 .△EFC 的面积=13⨯△EBC 的面积13=⨯210=70.所以4206701DEC EFC S FG GD S ∆===，所以6.7DG FD = △DGC 的面积=66140120.77DFC S ∆⨯=⨯=所以 四边形AEGD 的面积=四边形AECD 的面积-△DGC 的面积630120510.=-= 例14如图所示，直角三角形ACB 的两条直角边 AC 和BC 的长分别为14 cm 和28 cm ，CA 和 CB 分别绕点A 和B 点旋转 90至DA 和EB . 若DB 和AE 相交于点P ，求三角形P AB 的ABC DEP面积.（第17届华杯赛决赛初一网络版试题12）答：56.解：易知，45,DCA BCE ∠=∠=90,ACB ∠=所以，DCE 是一条直线.延长DA ，EB 相交于H . 则.DH EH ⊥12828421144232ABE ADEAH BES PB DP S AD EH ∆∆⨯⨯====⨯⨯，因此 44.437PB PB DB DP PB ===++而141498.2ADB ADC S S ∆∆⨯=== 所以449856.77PAB DAB S S ∆∆=⨯=⨯=例15．在△ABC 的边AB ，BC 和CA 上分别取点R ，P ，Q ，使得线段AP ，BQ 和CR 相交于一点M .证明：如果,,AMQ AMR BMR BMP CMP CMQ S S S S S S ∆∆∆∆∆∆===和那么M 是△ABC 三条中线的交点.证明：已知条件中给出的面积，我们通过右图中所示的S 1，S 2和S 3来表示. 因为△ARM 和△BRM 高相同， 所以12.S ARS RB = 类似可得13232,2S S AR S S RB +=+ 也就是12S AR S RB ==132322S S S S ++，由此推出 ()()12321322,S S S S S S +=+ ()3120,S S S ⇒-=因为30,S > 所以S 1=S 2，即AR=RB ，也就是CR 是△ABC 的一条中线.同理类似可证AP 和BQ 也是△ABC 的中线.因此M 是△ABC 三条中线的交点.例16. 如图，梯形ABCD 中，过对角线的交点O 引梯形两底的平行线分别交腰AD 、BC 于点M 和N . 求证：OM=ON.解：如图，连接MB ， 有NBD BOC AOD BMD S S S S ∆∆∆∆=== 在四边形MDNB 中， 因为NBD BMD S S ∆∆=，所以ON = OM .（思考：进一步可证2.ADN CBO S S ∆∆=）例17.在凸四边形ABCD 中，延长边AB 到1B ，使1BB AB =；延长BC 到1C ，使1CC BC =；延长CD 到1D ，使1DD CD =；延长DA 到1A ，使.1AA DA =请你证明：四边形1111D C B A 的面积是四边形ABCD 面积的5倍.证明： 由下左图，连接11,,,CA CB AD设12,.ABCACDS s Ss ==则1112,BB C Ss =1122,A DD Ss =所以11BB C S +11122()2A DD ABCD Ss s S =+=……①同理由上右图，连接11,,,C D BA BD 设34,.ABDBCDSs Ss ==则1132,A AB Ss =1142,C CD Ss =所以 11A AB S+11342()2C CD ABCD Ss s S =+=……②① + ②得 11BB C S+11A DD S+11A AB S +114C CD ABCD SS =所以 1111A B C D S =11(BB C S +11A DD S+11A AB S+11)5.C CD ABCD ABCD SS S +=例18． 如图，在直角ABC ∆的两直角边AC 、BC 上分别作正方形ACDE 和 CBFG . 连结AF 、BE 分别交 BC 、AC 于Q ，P . 求证：CP = CQ . 证明：注意AG = AC + CG = D C + CB = BD因为ABC BCE BPD ∆=∆=∆ ABC ACF AQG ∆=∆=∆所以AQG BPD ∆=∆ 即21BD ×CP =21AG ×CQ . 由于AG = BD ，所以CP = CQ.例19. 如右图所示, 四边形ABCD 的面积为6, 点M , N , P , Q 分别为各边的中点. 点O 为ABCD 内的一点. 连接OM 并延长至E 点, 使得2OM ME =, 同样的方式可得点F , G , H . 则四边形EFGH 的面积为 . 答: 27.解. 连接,,,MN NP PQ QM , 因为点,,,M N P Q 分别为四边形ABCD 各边的中点, 所以四边形MNPQ 的面积为四边形ABCD 面积的一半, 即四边形MNPQ 的面积为 3.因为2ME OM =且2NF ON =, 容易得到三角形OEF 的面积是三角OMN 的面积的9倍.同理可得三角形OFG 的面积是三角形ONP 的面 积的9倍；三角形OGH 的 面积是三角形OPQ 的面积 的9倍；三角形OHE 的面积是三角形OQM 的面积的9倍.所以四边形EFGH 的面积是四边形MNPQ 的面积9倍, 即四边形EFGH 的面积为27.例20．如图, 在五边形ABCDE 中, M ，N 分别是AB ，AE 的中点. 四边形AMPN ，△CPM ， △ CPD ，△DPN 的面积分别是9，6，9，6. 求五边形ABCDE 的面积.解：易知30.AMCDN S =连接MN ，设,MNP S x ∆=则:66:9x =推得 4.x =所以94 5.AMN S ∆=-=连接AC ，AD ，分别交MN 于F ，G . 由15//MCD NCD S S MN ∆∆==⇒CD . 在四边形AMCN 中， 51,462AMN CMN S AF FC S ∆∆===+ 同理可证1.2AG DG = 连接DF ，则6915.FCD MCD S S ∆∆==+=由于1,7.52AFD AF S FC ∆=⇒=，22.5.ACD S ∆= 因此3022.57.5.AMC AND AMCDN ACD S S S S ∆∆∆+=-=-= 由于M ，N 分别是AB ，AE 的中点，,,BMC AMC DNE AND S S S S ∆∆∆∆== 7.5.BMC DNE AMC AND S S S S ∆∆∆∆+=+=所以 ABCDE AMCDN BMC DNE S S S S ∆∆=++=30 +7.5 = 37.5. 例21. 平行四边形ABCD 的边AD 上 任取一点N ，过N 作平行于对角线AC 、 BD 的直线分别交边AB 、CD 于点M 和K.证明：三角形NMB 与NKC 等积.11。

等积变形有一个富翁留了一块三角形的土地给两个儿子，两个儿子要求平分这块地，这可伤透了他们的脑筋，因为他们不知道怎样去测量、平分。

同学们，你们能想出多少种方法将这块土地平分成个面积相等的三角形吗？根据这个问题，你能得出什么结论？结论一：。

思维探索例1：你有什么方法将任意一个三角形分成6个面积相等的三角形？如图，把△ABC的底边BC四等分，那么甲、乙两个三角形的面积谁大，为AB的面积是多少？如果△AC的面积是,那么AAB的面积是多少?如图，已知是BC的中点，是C的中点，是AC的中点。

已知三角形的面积是平方厘米，那么三角形ABC的面积是多少平方厘米？A思维探索例：（平行线间的等积变形）如下图，△和厶夹在一组平行线之间，且有公共底边，那么△和厶的面积关系是怎样的？结论拓展：夹在平行线间的一组同底三角形面积相等例：如图，在梯形中共有个三角形，其中面积相等的三角形有哪几对？即学即练如下图，在梯形A中，梯形A的面积是，AA的面积融会贯通例：如图，在直角三角形A中，D、E分别是A、A的中点，如果△AED的面积是即学即练如下图，在AA中，D、E是所在边的中点，如果AA的面积是,那么△DE的面积是多少？例：如图，A和DE都是长方形，A的长是厘米，的长是厘米。

那么图中阴影部分的面积是多少平方厘米？即学即练在边长为厘米的正方形中有一点，将点分别和四条边的中点相连，如下图，求阴影部分的面积。

练习册知识导航一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化。

同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状。

为便于实际问题的研究，我们还会常常用到以下结论：（）等底等高的两个三角形面积相等；（）底在同一条直线上并且相等，该底所对的角的的顶点是同一个点或在与底平行精彩文档如图, 是直角的直线上，这两个三角形面积相等；（）若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍。