等积变形习题

等积变形专项练习
1.在一个底面积是31.4平方厘米的长方体玻璃容器中，有一个底面半径是1厘米的圆锥形铝块完全浸在水中，当从水中取出铝块时，容器的水面下降了0.2厘米。

这个圆锥形铝块高多少厘米？
2.用半径10cm高7cm的圆柱形泥巴揉成半径一样大的圆锥形，圆锥的高是多少厘米呢？
3.一个圆柱形的水桶，内部的底面半径是20厘米，高是45厘米，里面盛有30厘米深的水。

将一个底面半径是15厘米的圆锥形铁块完全沉进水里，水不溢出，水面上升了3厘米，圆锥形铁块的高是多少？
4.有一段钢可做一个底面直径8厘米，高9厘米的圆柱形零件。

如果把它改制成高是12厘米的圆锥形零件，零件的底面积是多少平方厘米？
5.一个圆柱形容器的底面半径是4分米，高6分米，里面盛满水，把水倒在棱长是8分米的正方体容器中，水深多少分米？
6.将一个底面直径是20厘米、高是9厘米的金属圆锥，全部浸没在直径是40厘米的圆柱形水槽中且水未溢出。

水槽中的水面会升高多少厘米？
7.把一个长2米的圆柱截去4分米后，原先的外表积就削减了25.12平方分米，原先圆柱的体积是几何立方分米？
8.在一个底面是边长为2分米的正方形的长方形水槽中，放入一块青铜（完全浸没在水中），水面上升1分米且水未溢出。

（水槽厚度忽略不计）
1）求这块青铜的体积。

2）如果把这块青铜铸成一个底面直径是2分米的圆柱，它的高是多少？（得数保留一位小数）。

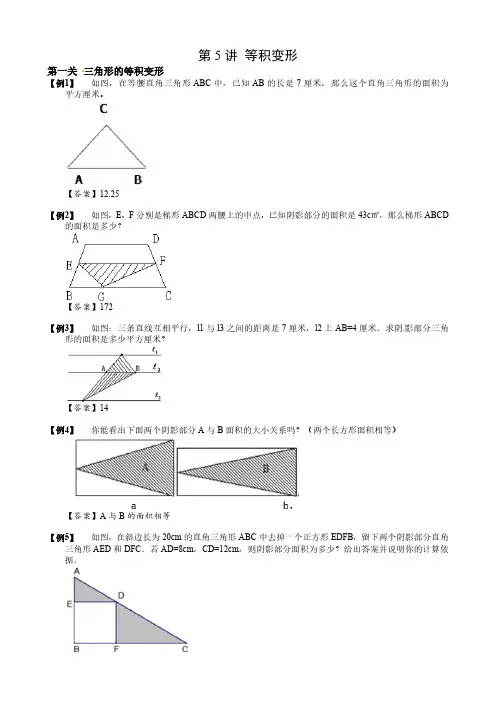
第5讲等积变形第一关三角形的等积变形【例1】如图，在等腰直角三角形ABC中，已知AB的长是7厘米，那么这个直角三角形的面积为　平方厘米。

【答案】12.25【例2】如图，E、F分别是梯形ABCD两腰上的中点，已知阴影部分的面积是43c㎡，那么梯形ABCD 的面积是多少？【答案】172【例3】如图：三条直线互相平行，l1与l3之间的距离是7厘米，l2上AB=4厘米．求阴影部分三角形的面积是多少平方厘米？　【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗？（两个长方形面积相等）【答案】A与B的面积相等【例5】如图，在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB，留下两个阴影部分直角三角形AED和DFC．若AD=8cm，CD=12cm，则阴影部分面积为多少？给出答案并说明你的计算依据．【答案】48【例6】如图，在直角三角形中有一个正方形，已知BD=10厘米，DC=7厘米，阴影部分的面积是多少？【答案】35平方厘米【例7】如图，梯形ABCD的面积是36，下底长是上底长的2倍，阴影三角形的面积是多少？【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大？【答案】图中甲乙的面积相等【例9】如图，在三角形ABC中，D是BC上靠近C的三等分点，E是AD中点，已知三角形ABC的面积为1，那么图中两个阴影三角形面积之和是多少？【答案】0.4【例10】已知△ABC面积为5，且BD=2DC，AE=ED，求阴影部分面积．要求写出关键的解题推理过程．【答案】2【例11】如图，将一个梯形分成四个三角形，其中两个三角形的面积分别为10与12．已知梯形的上底长度是下底的．请问：阴影部分的总面积是多少？【答案】23【例12】如图，已知梯形ABCD中，CD=10，梯形ABCD的高是4，那么阴影部分的面积是多少。

【答案】20【例13】（1）如图1，阴影部分的面积是多少？（2）如图2，一个长方形长4厘米，宽3厘米．A为长方形内的任意一点，阴影部分的面积是多少？【答案】（1）100；（2）6【例14】如图，在图中△ABE、ADF和四边形AECF面积相等．阴影部分的面积是多少？【答案】15【例15】如图，两个正方形（单位：厘米）中阴影部分的面积是多少平方厘米？【答案】8【例16】由面积为1，2，3，4的矩形拼成如图的长方形，图中阴影部分的面积为多少？【答案】【例17】如图所示，正方形ABCD的对角线BD长20厘米，BDFE是长方形．那么，五边形ABEFD的面积是多少平方厘米。

等积变形应用题等积变形应用题一“等积变形”是以形状改变而体积不变为前提.等积变形类应用题的基本关系式：变形前的体积（容积)＝变形后的体积(容积）.二练习题1、用直径为4cm的圆钢（截面为圆形的实心长条钢材）铸造3个直径为2cm,高为16cm的圆柱形零件，则需要截取多长的圆钢?2、某铜铁厂要锻造长、宽、高分别为260mm、150 mm、130 mm的长方体毛坯,需要截取地面积为130 mm2的方钢多长？3、某机器加工厂要锻造一个毛胚，上面是一个直径为20毫米，高为40毫米的圆柱,下面也是一个圆柱，直径为60毫米，高为20毫米，问需要直径为40毫米的圆钢多长?4、将一罐满水的直径为40厘米，高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里，问这时水的高度是多少？5、一个直径为1。

2米高为1.5米的圆柱形水桶，已装满水，向一个底面边长为1米的正方形铁盒倒水，当铁盒装满水时，水桶中的水高度下降了多少米。

6、有一块棱长为4厘米的正方体铜块，要将它熔化后铸成长2厘米、宽4厘米的长方体铜块，铸成后的铜块的高是多少厘米(不计损耗）？7 某工厂锻造直径为60毫米，高20毫米的圆柱形瓶内装水,再将瓶内的水倒入一个底面直径6厘米、高10厘米的圆柱形玻璃杯中,能否完全装下？若装不下，那么瓶内水面还有多高？若未能装满，求杯内水面离杯口的距离.8 有一个圆柱形铁块，底面直径为20厘米，高为26厘米,把它锻造成长方体毛胚，若使长方体的长为10π厘米，宽为13厘米，求长方体的高。

9 用一个底面半径为5厘米的圆柱形储油器，油液中浸有钢珠,若从中捞出546π克钢珠，问液面下降了多少厘米?(1立方厘米钢珠7.8克）10 小圆柱的直径是8厘米，高6厘米，大圆柱的直径是10厘米，并且它的体积是小圆柱体体积的2。

5倍，则大圆柱的高是多少厘米？11 一个长、宽、高分别是9厘米、7厘米、3厘米的长方体铁块和一个棱长为5厘米的正方体铁块，熔化成一个圆柱体,其底面直径为20厘米，请求圆柱体的高(π取3。

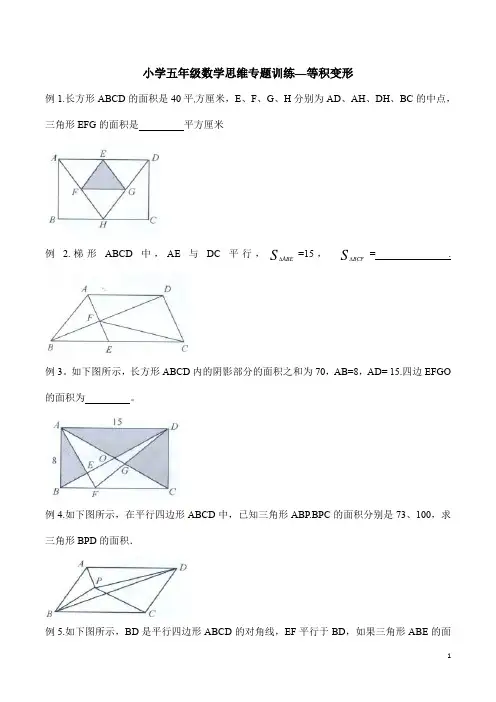
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米，E、F、G、H分别为AD、AH、DH、BC的中点，三角形EFG的面积是平方厘米例 2.梯形ABCD中，AE与DC平行，S ABE∆=15，S BCF∆= .例3。

如下图所示，长方形ABCD内的阴影部分的面积之和为70，AB=8，AD= 15.四边EFGO 的面积为。

例4.如下图所示，在平行四边形ABCD中，已知三角形ABP.BPC的面积分别是73、100，求三角形BPD的面积．例5.如下图所示，BD是平行四边形ABCD的对角线，EF平行于BD，如果三角形ABE的面积是12平方厘米，那么三角形AFD的面积是平方厘米。

例6.如下图所示，已知AE=EC，CD=DB，S ABC =60，求四边形FDCE的面积．例7.如右图所示，正方形ABC D和正方形ECGF并排放置，BF与CD相交于点H,已知AB=6厘米，则阴影部分的面积是平方厘米．例8.如下图所示，E、F、G、H分别是四边形ABCD各边的中点，EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积．试比较S1+S3与S2+S4的大小．例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份，长方形内任意一点与分点及顶点连结，如右图所示，则阴影部分的面积是 平方厘米．例10.右图所示ABCD 是个直角梯形（∠DAB=∠ABC= 900），以 ， AD 为一边向外作长方形ADEF ，其面积为6.36平方厘米，连接BE 交AD 于P ，再连接PC ．则图中阴影部分的面积是 平方厘米。

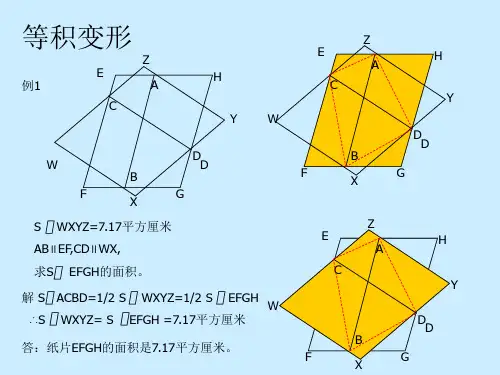
A.6.36B.3.18C.2.12D.1.59例11.如下图所示，平行四边形内有两个大小一样的正六边形，那么阴影部分的面积占平行四边形面积的 。

A ．21B ．32C ．52D ．125例12.如下图所示，矩形ABCD 的面积是24平方厘米，三角形ADM 与三角形BCN 的面积之和是7.8平方厘米，则四边形PMON 的面积是 平方厘米．例13.一个矩形分成4个不同的三角形（如下图），绿色三角形面积占矩形面积的15%，黄色三角形的面积是21平方厘米．问：矩形的面积是多少平方厘米？例14.如下图所示，正方形每条边上的三个点（端点除外）都是这条边的四等分点，则阴影部分的面积是正方形面积的。

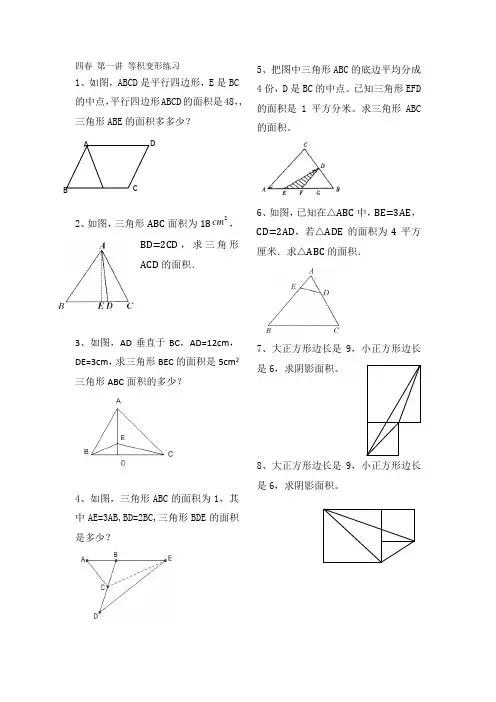
四春 第一讲 等积变形练习
1、如图，ABCD 是平行四边形，E 是BC 的中点，平行四边形ABCD 的面积是48，,三角形ABE 的面积多多少？
2、如图，三角形ABC 面积为182
cm ，
BD=2CD ，求三角形ACD 的面积．
3、如图，AD 垂直于BC ，AD=12cm ，DE=3cm ，求三角形BEC 的面积是5cm 2三角形ABC 面积的多少？
4、如图，三角形ABC 的面积为1，其中AE=3AB,BD=2BC,三角形BDE 的面积是多少？
5、把图中三角形ABC 的底边平均分成4份，D 是BC 的中点。

已知三角形EFD 的面积是1平方分米。

求三角形ABC 的面积。

6、如图，已知在△ABC 中，BE=3AE ，CD=2AD ，若△ADE 的面积为4平方厘米．求△ABC 的面积．
7、大正方形边长是9，小正方形边长是6，求阴影面积。

8、大正方形边长是9，小正方形边长是6，求阴影面积。

等积变形的应用——两道赛题的解法赛题一：给定一个三角形ABC，给定它的边长a，b，c，要求把它变形成一个等腰直角三角形，且其新的三边为x，x，y。

解题思路：由等积变形定理可知，三角形ABC与新三角形ABC满足：$$\frac{a}{\sin A} = \frac{x}{\sin A'} = \frac{x}{\sin B'} = \frac{y}{\sin C'}$$解出新的三角形边长x，y的差分方程为：$$a\cdot\sin A = x\cdot\sin B = x\cdot\sin C = y\cdot\sinA'$$解得：$$x = \frac{a \cdot \sin A}{\sin B} = \frac{a \cdot \sinA}{\sin C}$$$$y = \frac{a \cdot \sin A}{\sin A'}$$赛题二：给定一个三角形ABC，给定它的边长a，b，c，要求把它变形成一个三角形，且其新的三边为x，y，z。

解题思路：由等积变形定理可知，三角形ABC与新三角形ABC满足：$$\frac{a}{\sin A} = \frac{x}{\sin A'} = \frac{y}{\sin B'} = \frac{z}{\sin C'}$$解出新的三角形边长x，y，z的差分方程为：$$a\cdot\sin A = x\cdot\sin A' = y\cdot\sin B' = z\cdot\sin C'$$解得：$$x = \frac{a \cdot \sin A}{\sin A'}$$$$y = \frac{a \cdot \sin A}{\sin B'}$$$$z = \frac{a \cdot \sin A}{\sin C'}$$。

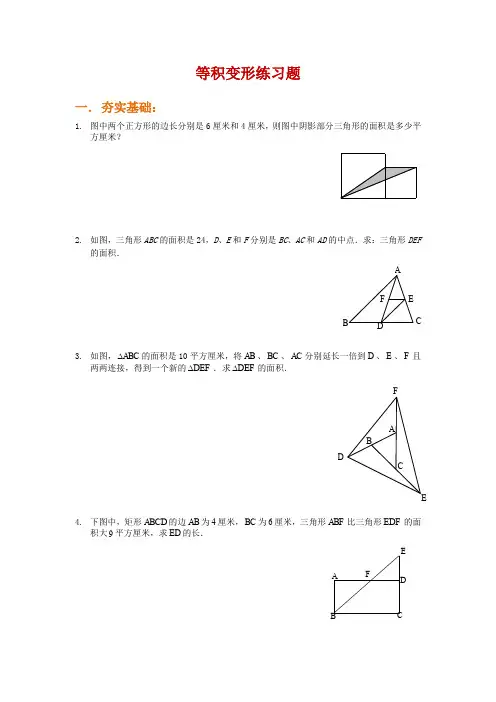
等积变形练习题一． 夯实基础：1. 图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是多少平方厘米？2. 如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求：三角形DEF的面积．3. 如图，ABC ∆的面积是10平方厘米，将AB 、BC 、AC 分别延长一倍到D 、E 、F 且两两连接，得到一个新的DEF ∆．求DEF ∆的面积．4. 下图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形EDF 的面积大9平方厘米，求ED 的长．B ACDEFFE DCBA FEDCBA5. 图中4CA AB ==厘米，三角形ABE 比三角形CDE 的面积大2平方厘米，求CD 的长．二． 拓展提高：6. 在图中，平行四边形ABCD 的边BC 长10厘米，直角三角形ECB 的直角边EC 长8厘米．已知阴影部分的总面积比三角形EFG 的面积大10平方厘米，求平行四边形ABCD 的面积．7. 如图，ABCD 是边长为8厘米的正方形，梯形AEBD 的对角线相交于O ，三角形AOE 的面积比三角形BOD 的面积小16平方厘米，则梯形AEBD 的面积是多少平方厘米？AB CDEO8. 如图，在长方形ABCD 中，Y 是BD 的中点，Z 是DY 的中点，如果24AB =厘米，8BC =厘米，求三角形ZCY 的面积．EDCB AYZ DCBA9. 如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AF CF =，三角形AFE (图中阴影部分)的面积为8 平方厘米．平行四边形的面积是多少平方厘米？10. 如图，ABCD 与AEFG 均为正方形，三角形ABH 的面积为6平方厘米，图中阴影部分的面积为多少平方厘米？三. 超常挑战11. 如图，O 是长方形ABCD 内一点，已知OBC 的面积是52cm ，OAB 的面积是22cm ，求OBD 的面积是多少？12. 如下图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？13. 如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．FCH14. 如图所示，ABC ∆中，90ABC ∠=︒，3AB =，5BC =，以AC 为一边向ABC ∆外作正方形ACDE ，中心为O ，求OBC ∆的面积．四．杯赛演练：15. (《小数报》数学竞赛)如图，梯形ABCD 被它的一条对角线BD 分成了两部分．三角形BDC的面积比三角形ABD 的面积大10平方分米．已知梯形的上底与下底的长度之和是15分米，它们的差是5分米．求梯形ABCD 的面积．16. (西城某重点中学小升初分班考题)下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC 的面积．EDCBAFED CBA答案：1. 4428⨯÷=．2. 三角形ADC 的面积是三角形ABC 面积的一半24212÷=，三角形ADE 又是三角形ADC 面积的一半1226÷=．三角形FED 的面积是三角形ADE 面积的一半，所以三角形FED 的面积623=÷=．3. 根据题意可知，2ADF ABC S S ∆∆=，同理可知2BDE CEF ABC S S S ∆∆∆==，于是(123)771070DEF ABCABCS SS∆=+⨯==⨯=平方厘米．4. (469)6241⨯-÷⨯-=（厘米）5. 连结CB ．三角形DCB 的面积为44226⨯÷-=（平方厘米），6423CD =÷⨯=（厘米）．6. 因为阴影部分比三角形EFG 的面积大10平方厘米，都加上梯形FGCB 后，根据差不变性质，所得的两个新图形的面积差不变，即平行四边形ABCD 比直角三角形ECB 的面积大10平方厘米,所以平行四边形ABCD 的面积等于10821050⨯÷+=平方厘米．7. 题目中出现了两个三角形面积之差16，若将AOD ∆作为公共部分分别加给这两个三角形后，根据差不变原理可知，AED ∆的面积比BAD ∆的面积小16平方厘米,而BAD ∆正好是正方形面积的一半即88232⨯÷=(平方厘米)，从而AED ∆的面积为321616-=（平方厘米）．作为梯形的另一部分，EBD ∆的面积与BAD ∆面积相等（同底等高）． 可见，梯形的面积=163248+=(平方厘米).8. ∵Y 是BD 的中点，Z 是DY 的中点224ZCY DCB ZY DB S S ∴=÷÷=÷，又∵ABCD 是长方形，∴42424ZCYDCBABCD SSS =÷=÷÷=长方形(平方厘米)．9. 连接FB ．三角形AFB 面积是三角形CFB 面积的2倍，而三角形AFB 面积是三角形AEF面积的2倍，所以三角形ABC 面积是三角形AEF 面积的3倍；又因为平行四边形的面积是三角形ABC 面积的2倍，所以平行四边形的面积是三角形AFE 面积的326⨯=（）倍．因此，平行四边形的面积为8648⨯=(平方厘米)．10. 如图，连接AF ，比较ABF ∆与ADF ∆，由于AB AD =，FG FE =，即ABF ∆与ADF ∆的底与高分别相等，所以ABF ∆与ADF ∆的面积相等，那么阴影部分面积与ABH ∆的面积相等，为6平方厘米．F11. 设AODSX =，因为12AOBDOCAODBOCABCD SSSSS +=+=所以可得：25DOC S X +=+，即3DOC S X =+ 另有253102ABCD AOB DOC AOD BOC S S S S S X X X =+++=++++=+（）所以152ABD ABCD S S X ==+,可得523OBD ABD AOB AOD S S S S X X =--=+--=(2cm )．12. 根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差． 如下图，连接CP 、AP ．由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=，所以BCP ABP BDP S S S ∆∆∆-=．而12BCP BCFE S S ∆=，12ABP ABHG S S ∆=，所以()2216BCFE ABHG BCP ABP BDP S S S S S ∆∆∆-=-==(平方分米)．13. 本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ． ∵AE EB =， ∴S S AEH BEH =．同理，S S BFH CFH =，S =S CGH DGH ，∴11S S 562822==⨯=阴影长方形ABCD （平方厘米）．14. 如图，将OAB ∆沿着O 点顺时针旋转90︒，到达OCF ∆的位置．由于90ABC ∠=︒，90AOC ∠=︒，所以180OAB OCB ∠+∠=︒．而OCF OAB ∠=∠， 所以180OCF OCB ∠+∠=︒，那么B 、C 、F 三点在一条直线上．由于OB OF =，90BOF AOC ∠=∠=︒，所以BOF ∆是等腰直角三角形，且斜边BF 为538+=，所以它的面积为218164⨯=．CH E BA根据面积比例模型，OBC ∆的面积为516108⨯=．15. 方法一：如右图，作AB 的平行线DE ．三角形BDE 的面积与三角形ABD 的面积相等，三角形DEC 的面积就是三角形BDC 与三角形ABD 的面积差(10平方分米)．从而，可求出梯形高(三角形DEC 的高)是：21054⨯÷=(分米)，梯形面积是：154230⨯÷=(平方分米)． 方法二：10330⨯=(平方分米)．16. 连结AD (见右上图)，可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形AFD 是三角形ABD 与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABF 与三角形FCD 面积仍然相等．根据等量代换，求三角形ABC 的面积等于求三角形BCD 的面积，等于4428⨯÷=（平方厘米）．ABCDEF。

等积变形有一个富翁留了一块三角形的土地给两个儿子，两个儿子要求平分这块地，这可伤透了他们的脑筋，因为他们不知道怎样去测量、平分。

同学们，你们能想出多少种方法将这块土地平分成个面积相等的三角形吗？根据这个问题，你能得出什么结论？结论一：。

思维探索例1：你有什么方法将任意一个三角形分成6个面积相等的三角形？如图，把△ABC的底边BC四等分，那么甲、乙两个三角形的面积谁大，为AB的面积是多少？如果△AC的面积是,那么AAB的面积是多少?如图，已知是BC的中点，是C的中点，是AC的中点。

已知三角形的面积是平方厘米，那么三角形ABC的面积是多少平方厘米？A思维探索例：（平行线间的等积变形）如下图，△和厶夹在一组平行线之间，且有公共底边，那么△和厶的面积关系是怎样的？结论拓展：夹在平行线间的一组同底三角形面积相等例：如图，在梯形中共有个三角形，其中面积相等的三角形有哪几对？即学即练如下图，在梯形A中，梯形A的面积是，AA的面积融会贯通例：如图，在直角三角形A中，D、E分别是A、A的中点，如果△AED的面积是即学即练如下图，在AA中，D、E是所在边的中点，如果AA的面积是,那么△DE的面积是多少？例：如图，A和DE都是长方形，A的长是厘米，的长是厘米。

那么图中阴影部分的面积是多少平方厘米？即学即练在边长为厘米的正方形中有一点，将点分别和四条边的中点相连，如下图，求阴影部分的面积。

练习册知识导航一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化。

同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状。

为便于实际问题的研究，我们还会常常用到以下结论：（）等底等高的两个三角形面积相等；（）底在同一条直线上并且相等，该底所对的角的的顶点是同一个点或在与底平行精彩文档如图, 是直角的直线上，这两个三角形面积相等；（）若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍。

六年级数学等积变形1，一个盛水的圆柱形水桶,内底面周长为6028分米，当一个长方形的物体投入水中时，水面上升1分米，量得这个长方体的长为3；14分米，宽为1分米，他的高是多少？2,在长为15厘米，宽为12厘米的长方体水箱中，有10厘米深的水，现沉入一个高为10厘米的圆锥形铁块《全部浸入水中》，水面上升了2厘米，求圆锥的底面积?3,甲，乙两个圆柱体容器，底面积比为4:3,甲容器水深7厘米，以容器水深3厘米，再往两容器中各注入同样多的水，直到水深相等，这时水深多少厘米？4，一个棱长为1分米的正方体木块，从这个木块中各出一个最大的圆锥,求这个圆锥的表面积和体积？5，用一张长3米宽1米的长方形铁皮可以做成无底的圆柱形管子，此圆柱形管子的最大面积是多少？6，一个胶水瓶，它的瓶身呈圆柱形《不包括瓶颈》，容积是32；4立方厘米，当瓶子正放时，瓶内胶水深为8厘米，瓶子倒放时，空余部分为2厘米，则瓶内所装水的体积是多少？7；有A；B两个圆柱形容器，最初在容器A里装有2升水，容器B是空的。

现在往两个容器中以每分钟0；4升的流量注入水，4分钟后，两个容器的水面高度相等。

设B的底面半径为5厘米，那么A的底面直径是多少厘米？8；将一个圆柱体木块沿上下底面圆心切成四块，表面积增加48平方厘米；若将这个圆柱体切成三块小圆柱体，表面积增加50；24平方厘米。

现在把这个圆柱体木块削成一个最大的圆锥体，体积减少多少立方厘米？9；圆钢切削成一个最大的圆锥体，切削掉的部分部分重8千克，这段圆钢重多少㎏？10；棱长是4分米的立方体钢坯切削成一个最大的圆柱，这个圆柱的体积是多少立方分米？11；一个体积为60立方厘米的圆柱，削成一个最大的圆锥，这个圆锥的体积是多少立方厘米？12；一车箱是长方体，长4米，宽1；5米，高4分米，装满沙，堆成一个高5分米的圆锥，底面积多少㎡13；一个底面周长15；7m高10m的圆柱铁块，熔成一个底面积是25㎡的圆锥，圆锥的高是多少m？14；把一个体积是18㎝³的圆柱削成一个最大的圆锥，削成的圆锥体积是多少㎝³？15；正方体钢材，棱长6分米，把它削成一个最大的圆锥体零件，零件的体积是多少?。

等积变换1、等面积图形拼接类1、小明遇到一个问题：5个同样大小的正方形纸片排列形式如图1所示，将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后，将三角形纸片①绕AB 的中点O 旋转至三角形纸片②处，依此方法继续操作，即可拼接成一个新的正方形DEFG .请你参考小明的做法解决下列问题：（1）现有5个形状、大小相同的矩形纸片，排列形式如图3所示.请将其分割后拼接成一个平行四边形．要求：在图3中画出并指明拼接成的平行四边形（画出一个．．符合条件的平行四边形即可）；（2）如图4，在面积为2的平行四边形ABCD 中，点E 、F 、G 、H 分别是边AB 、 BC 、CD 、DA 的中点，分别连结AF 、BG 、CH 、DE 得到一个新的平行四边形MNPQ .请在图4中探究平行四边形MNPQ 面积的大小（画图．．并直接写出结果）.2、根据所给的图形解答下列问题：（1）如图1，△ABC 中，AB=AC ，∠BAC =90°，AD ⊥BC 于D ，把△ABD 绕点A旋转，图1图2图3图4并拼接成一个与△ABC 面积相等的正方形,请你在图１中完成这个作图；（2）如图2，△ABC 中，AB=AC ，∠BAC =90°，请你设计一种与(1)不同的方法，将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得到的正方形；（3）设计一种方法把图3中的矩形ABCD 拆分并拼接为一个与其面积相等的正方形, 请你依据此矩形画出正方形，并根据你所画的图形，证明正方形面积等于矩形ABCD 的面积的结论.A BCD图3图2图1CBAAB CD2、等分面积类问题1、请作一条直线通过割补把下面的四边形变成面积相等的三角形2、如图，一块矩形的铁皮ABCD 被割去一个小矩形部分DEFG ，剩下一个五边形ABCGFE ，请作一条直线把剩下的五边形分成面积相等的两部分BCADG E D BCFAABCDAD3、（1）请过△ABC 边BC 中点D 作一条直线平分△ABC 的面积（2）请过△ABC 边BC 中点D 外任一点P 作一条直线平分△ABC 的面积4、如图，梯形纸片ABCD 中，AD ∥BC 且AB DC.设AD=a,BC=b. 过AD 中点和BC 的中点的直线可将梯形纸片ABCD 面积分成面积相等的两部分. 请你再设计一种方法:只须用剪子剪一次将梯形纸片ABCD 分割成面积相等的二部分，画出设计的图形并简要说明你的分割方法.DBCADBCAP5、如图是王大爷的一块四边形菜地，在A处有一口井，王大爷要想从A处引一条笔直的水渠，且这条笔直的水渠将四边形菜地分成面积相等的两部分.请你为王大爷设计一条引水渠的方案，画出图形,并简要写出作图的主要步骤.Welcome To Download !!!欢迎您的下载，资料仅供参考！。

五年级等积变形题一、等积变形题目。

1. 一个长方体水箱，从里面量长6分米，宽5分米，高4分米。

先倒入82升水，再浸入一块棱长2分米的正方体铁块，这时水面离水箱口1分米。

求水箱的容积是多少升？- 解析：正方体铁块体积为2×2×2 = 8立方分米，因为1立方分米= 1升，所以8立方分米= 8升。

倒入水的体积是82升，此时水和铁块总体积为82+8=90升。

水面离水箱口1分米，则此时水和铁块占水箱的高度是4 - 1=3分米。

水箱底面积为6×5 = 30平方分米，根据长方体体积公式V=Sh（S是底面积，h是高），那么3分米高的水和铁块的体积对应的水箱容积部分为30×3 = 90升，所以水箱容积为90÷3×4 = 120升。

2. 有一个底面积是300平方厘米、高10厘米的长方体，里面盛有5厘米深的水。

现在把一块石头浸没到水里，水面上升2厘米。

这块石头的体积是多少立方厘米？- 解析：因为石头浸没到水中，水面上升的体积就是石头的体积。

长方体底面积是300平方厘米，水面上升了2厘米，根据长方体体积公式V = Sh，石头体积为300×2=600立方厘米。

3. 一个正方体容器棱长为6分米，里面装满水。

现将水倒入一个长0.8米、宽0.6米的长方体容器中，水面高多少分米？- 解析：首先统一单位，0.8米= 8分米，0.6米= 6分米。

正方体容器棱长6分米，则水的体积为6×6×6 = 216立方分米。

将水倒入长方体容器中，长方体容器底面积为8×6 = 48平方分米，根据h=(V)/(S)（h是高，V是体积，S是底面积），水面高度为216÷48 = 4.5分米。

4. 把一块棱长12厘米的正方体铁块熔铸成一个底面积是144平方厘米的长方体铁块，这个长方体铁块的高是多少厘米？- 解析：正方体铁块体积为12×12×12 = 1728立方厘米。