牛顿粘性定律
- 格式:doc
- 大小:150.00 KB
- 文档页数:3




牛顿黏性实验定律
牛顿黏性实验定律是物理学家牛顿在17th世纪提出的一条定律,它描述了物体在受到外力作用时的运动规律。
它规定,当一个物体受到外力作用时,它的运动受到两种力的影响:一种是外力,另一种是物体自身的黏性力。
物体的运动受到这两种力的共同作用,它的运动规律可以用下面的公式来表示:F=ma+bv,其中F表示外力,m表示物体的质量,a表示物体的加速度,b表示物体的黏性系数,v表示物体的速度。
牛顿黏性实验定律的发现对物理学的发展有着重要的意义,它为研究物体在受到外力作用时的运动规律提供了一个重要的理论框架。
它不仅可以用来研究物体的运动规律,而且还可以用来研究物体的变形、振动和摩擦等问题。
牛顿黏性实验定律的发现也为现代物理学的发展提供了重要的理论基础,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
牛顿黏性实验定律的发现也为现代物理学的发展提供了重要的理论基础,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
牛顿黏性实验定律的发现也为现代物理学的发展提供了重要的理论基础,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
牛顿黏性实验定律的发现为物理学的发展做出了重要贡献,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
它的发现也为现代物理学的发展提供了重要的理论基础,为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。

牛顿黏性实验定律的简单解释牛顿粘性实验定律,顾名思义,是以牛顿为代表的人所做的有关大小均匀的物体在受到外力作用时总会发生运动状态变化。
牛顿在《自然哲学的数学原理》中写道:“我想,如果某种物体,对地面的压力同它所受的重力成比例,这个物体就可能在不需要外力的推动下而发生运动。
但是,如果这种物体受到的重力和它所受的压力成比例,那么它就没有发生运动的趋势了,即当它停止下来的时候,速度为零。
”“第二实验”指的是,将两个铁球分别放置在固定在平板上的木架上,并使其保持相互平行的位置。
在离两球中点距离相等的地方画一线,此时若拉绳,让它绕过两球的中点,则只有一个球发生移动,另一个球被拖动,且动的越快,动得越远。
即两球中任何一个是相对静止的。
牛顿黏性实验定律说明,当两个不同质量的物体之间相互接触或靠近时,接触面会发生形变,从而出现一系列效应:( 1)一个物体将另一个物体紧紧包围起来,两者间有弹力;( 2)两个物体在相互挤压时有摩擦力;( 3)两个物体相互接触时产生附加力,当其它因素不变时,随着两物体间距离的增大,它们的相互作用力也随之增大,从而会导致两物体间出现剪切力,同时还会产生相互作用力,进一步增大了力的作用效果。
也就是说,物体与物体之间存在引力和斥力,所谓万有引力就是指的这种相互作用力。
“第一实验”指的是地面上有一条绳子或薄板,下面悬挂着轻质的东西(不计空气阻力,忽略摩擦力,忽略绳子弹性的影响),同时还给予向上的拉力F=-N。
当物体A放在薄板上时, F很小,由于地球引力作用,它将静止不动;若将物体B放在薄板上,那么根据万有引力的公式F=-N,所以对B施加一个很大的向下的拉力F=-M,在两力的作用下, A和B一起向下运动,并处于相对静止状态。
此时,物体A和B的距离是变小的,力的大小也会减少,因为两物体间的引力和斥力都在逐渐减弱,直至消失,那么此时两物体就会[gPARAGRAPH3],就是互相靠近、合拢,而并非是像上面一样靠拢、分开。
⽜顿粘性定律与流体的粘度流体的流动现象--⽜顿粘性定律与流体的粘度⼯业⽣产中的许多过程都与流体的流动现象密切相关,流动现象是个极为复杂的问题,涉及⾯⼴,本节只作简要的介绍。
⼀、⽜顿粘性定律前已述及,流体具有流动性,即没有固定形状,在外⼒作⽤下其内部产⽣相对运动。
另⼀⽅⾯,在运动的状态下,流体还有⼀种抗拒内在的向前运动的特性,称为粘性,粘性是流动性的反⾯。
以⽔在管内流动时为例,管内任⼀截⾯上各点的速度并不相同,中⼼处的速度最⼤,愈靠近管壁速度愈⼩,在管壁处⽔的质点附于管壁上,其速度为零。
其他流体在管内流动时也有类似的规律。
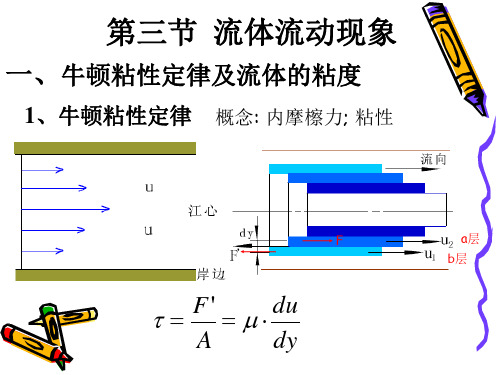
所以,流体在圆管内流动时,实际上是被分割成⽆数极薄的圆筒层,⼀层套着⼀层,各层以不同的速度向前运动,如图1-10所⽰。
由于各层速度不同,层与层之间发⽣了相对运动,速度快的流体层对与之相邻的速度较慢的流体层发⽣了⼀个推动其向前运动⽅向前进的⼒,⽽同时速度慢的流体层对建度快的流体层也作⽤着⼀个⼤⼩相等,⽅向相反的⼒,从⽽阻碍较快的流体层向前运动。
这种运动着的流体内部相邻两流体层间的相互作⽤⼒,称为流体的内摩擦⼒,是流体粘性的表现,所以⼜称为粘滞⼒或粘性摩擦⼒。
流体在流动时的内摩擦,是流动阻⼒产⽣的依据,流体流动时必须克服内摩擦⼒⽽作功,从⽽将流体的⼀部分机械能转变为热⽽损失掉。
流体流动时的内摩擦⼒⼤⼩与哪些因素有关?可通过下⾯情况加以说明。
图1-10 流体在圆管内分层流动⽰意图图1-11 平板间液体速度变化图如图1-11所⽰,设有上下两块平⾏放置且⾯积很⼤⽽相距很近的平板,板间充满了某种液体。
若将下板固定,⽽对上板施加⼀个恒定的外⼒,上板就以恒定的速度u沿x⽅向运动。
此时,两板间的液体就会分成⽆数平⾏的薄层⽽运动,粘附在上板底⾯的⼀薄层液体也以建度。
随上板⽽运动,其下各层液体的速度依次降低,粘附在下板表⾯的液层速度为零。
实验证明,对于⼀定的液体,内摩擦⼒F与两流体层的速度差Δu成正⽐,与两层之间的垂直距离Δy 成反⽐,与两层间的接触⾯积S成正⽐,即:若把上式写成等式,就需引进⼀个⽐例系数µ,即:式中的内摩擦⼒F与作⽤⾯S平⾏。
牛顿粘性定律表达式
牛顿粘性定律是一种物理定律,它描述了流体或固体在不同情况下表现出的粘].它有3种主要表达方式:
1. 牛顿第一定律:
牛顿第一定律(简称“牛顿定律”)声明:如果一个流体或固体体系没有外力影响,那么体系的运动会保持平衡,也就是说不会有变化。
它的表达式为:F = m · a
2. 牛顿第二定律:
牛顿第二定律(简称“牛顿力定律”)声明:当物体在受到外力影响作用力时,物体就会发生总加速度。
它的表达式为:F = m ·(a + α)
3. 牛顿粘性定律:
牛顿粘性定律对物理学中的流体或固体的粘性力及其作用力做出定义和解释,它与牛顿力定律具有一定的联系。
它的表达式为:F = -κ · V
在物理实验中,我们可以更快地掌握牛顿粘性定律的基本原理:一个物体在固定的条件下会像其周围的一样,运动更慢一些,也就是说,其减慢的程度可以用粘性力来描述;当物体受到外力作用时,受到外力的粘性作用会影响其最终运动形式及加速度,从而可以用V=F/K表
示,其中,V表示运动后的熟悉,K为物体粘性常数。
粘性定律中涉及三个量:外力F,粘性力K和熟悉V。
综上所述,牛顿粘性定律的表达式为:F = m · a ; F = m ·(a + α) ;F = -κ · V 。
它们三者一起构成了物体运动规律中粘性力的定义与解释。
牛顿粘性定律
牛顿在1687年进一步假设:流体内摩擦力与两层流体间的相对速度成正比。
图B1.3.6
以平行平板流动为例<图B1.3.6),下板静止,上板速度δu,按不滑移假设,δt时间后,矩形元ABCD变形为平行四边形A'BCD'。
间距为δy的两层流体的相对速度称为速度梯度: b5E2RGbCAP
(B1.3.1>
称为角变形率或剪切变形率。
设x方向单位面积上的流体内摩擦力为τ,称为粘性切应力。
按牛顿粘性假设:
(B1.3.2>
比例系数μ称为粘度。
粘度为常数的流体称为牛顿流体。
据牛顿粘性假设和不滑移假设求解流体运动方程<B3.4),理论结果与实验吻合,验证了两个假设的合理性,因此前者<B1.3.2)式称为牛顿粘性定律,后者称为不滑移条件。
p1EanqFDPw
粘度的全称为动力粘度或绝对粘度。
牛顿流体的粘度可由<B1.3.2)式决定:
(B1.3.3>△在SI中粘度的单位是N·s/m2或Pa·s<帕秒);
在cgs制中粘度的单位是g / cm·s 或p<泊)。
1N·s/m2 =10g / cm·s 或1Pa·s =10 p
图B1.3.7
温度对流体的粘性影响较大:液体的粘度随温度升高而减小,气体则相反。
运动粘度定义为动力粘度与密度之比值:
(B1.3.4>
△ 在SI制中运动粘度的单位是m 2 / s ;
在cgs制中运动粘度的单位是cm 2 / s。
申明:
所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。