选修2-1双曲线及其标准方程课时作业

§2.3 双曲线2．3.1 双曲线及其标准方程一、选择题1．双曲线方程为x 2－2y 2＝1，则它的右焦点坐标为( )A.⎝⎛⎭⎫22，0B.⎝⎛⎭⎫62，0C.⎝⎛⎭⎫52，0D ．(3，0) 考点 双曲线的标准方程题点 由双曲线方程求参数[答案] B[解析] 将双曲线方程化为标准方程为x 2－y 212＝1， ∴a 2＝1，b 2＝12，∴c 2＝a 2＋b 2＝32，∴c ＝62， 故右焦点坐标为⎝⎛⎭⎫62，0. 2．已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点分别为F 1，F 2，点P 在双曲线的右支上，若|PF 1|－|PF 2|＝b ，且双曲线的焦距为25，则该双曲线的方程为( )A.x 24－y 2＝1B.x 23－y 22＝1C ．x 2－y 24＝1 D.x 22－y 23＝1 考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程[答案] C[解析] 由题意得⎩⎪⎨⎪⎧ |PF 1|－|PF 2|＝2a ＝b ，c 2＝a 2＋b 2，2c ＝25，解得⎩⎪⎨⎪⎧a 2＝1，b 2＝4， 则该双曲线的方程为x 2－y 24＝1. 3．已知双曲线x 2a －3＋y 22－a＝1，焦点在y 轴上，若焦距为4，则a 等于( ) A.32B ．5C ．7D.12考点 双曲线的标准方程题点 由双曲线方程求参数[答案] D[解析] 根据题意可知，双曲线的标准方程为y 22－a －x 23－a＝1. 由其焦距为4，得c ＝2，则有c 2＝2－a ＋3－a ＝4，解得a ＝12. 4．已知双曲线x 24－y 25＝1上一点P 到左焦点F 1的距离为10，则PF 1的中点N 到坐标原点O 的距离为( )A ．3或7B ．6或14C ．3D ．7考点 双曲线的定义题点 双曲线定义的应用[答案] A[解析] 连接ON ，ON 是△PF 1F 2的中位线，∴|ON |＝12|PF 2|，∵||PF 1|－|PF 2||＝4，|PF 1|＝10，∴|PF 2|＝14或6，∴|ON |＝12|PF 2|＝7或3. 5．“mn <0”是方程“mx 2＋ny 2＝1表示双曲线”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件考点 双曲线的标准方程题点 已知曲线方程判断曲线的形状[答案] C[解析] 因为mn <0，所以m ，n 均不为0且异号，方程mx 2＋ny 2＝1，可化为x 21m ＋y 21n＝1，因为1m 与1n 异号，所以方程x 21m ＋y 21n＝1表示双曲线，故“mn <0”是“方程mx 2＋ny 2＝1表示双曲线”的充分条件；反之，若mx 2＋ny 2＝1表示双曲线，则其方程可化为x 21m ＋y 21n＝1，可知1m 与1n异号，则必有mn <0，故“mn <0”是“方程mx 2＋ny 2＝1表示双曲线”的必要条件．综上可得，“mn <0”是方程“mx 2＋ny 2＝1表示双曲线”的充要条件．6．已知平面内两定点A (－5,0)，B (5,0)，动点M 满足|MA |－|MB |＝6，则点M 的轨迹方程是( ) A.x 216－y 29＝1 B.x 216－y 29＝1(x ≥4) C.x 29－y 216＝1 D.x 29－y 216＝1(x ≥3) 考点 求与双曲线有关的轨迹方程题点 双曲线的一支[答案] D[解析] 由|MA |－|MB |＝6，且6<|AB |＝10，得a ＝3，c ＝5，b 2＝c 2－a 2＝16.故其轨迹为以A ，B 为焦点的双曲线的右支．所以方程为x 29－y 216＝1(x ≥3)． 7．动圆与圆x 2＋y 2＝1和x 2＋y 2－8x ＋12＝0都外切，则动圆圆心的轨迹是( )A ．双曲线的一支B ．圆C ．椭圆D ．双曲线 考点 双曲线的定义题点 双曲线定义的应用[答案] A[解析] 设动圆的圆心为M ，半径为r ，圆x 2＋y 2＝1与x 2＋y 2－8x ＋12＝0的圆心分别为O 1和O 2，半径分别为1和2，由两圆外切的充要条件，得|MO 1|＝r ＋1，|MO 2|＝r ＋2.∴|MO 2|－|MO 1|＝1，又|O 1O 2|＝4，∴动点M 的轨迹是双曲线的一支(靠近O 1)．8．若双曲线x 2n－y 2＝1(n >1)的左、右焦点分别为F 1，F 2，点P 在双曲线上，且满足|PF 1|＋|PF 2|＝2n ＋2，则△PF 1F 2的面积为( )A ．1B.12C ．2D ．4 考点 双曲线的定义题点 双曲线的焦点三角形[答案] A[解析] 设点P 在双曲线的右支上，则|PF 1|－|PF 2|＝2n ，已知|PF 1|＋|PF 2|＝2n ＋2， 解得|PF 1|＝n ＋2＋n ，|PF 2|＝n ＋2－n ， |PF 1|·|PF 2|＝2.又|F 1F 2|＝2n ＋1，则|PF 1|2＋|PF 2|2＝|F 1F 2|2，∴△PF 1F 2为直角三角形，∠F 1PF 2＝90°，∴12PF F S △＝12|PF 1|·|PF 2|＝12×2＝1.二、填空题9．以椭圆x 23＋y 24＝1的焦点为顶点，以这个椭圆的长轴的端点为焦点的双曲线的标准方程是________．考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程[答案] y 2－x 23＝1 [解析] 由题意知，双曲线的焦点在y 轴上，且a ＝1，c ＝2，所以b 2＝3，所以双曲线的方程为y 2－x 23＝1. 10．若曲线C ：mx 2＋(2－m )y 2＝1是焦点在x 轴上的双曲线，则m 的取值范围为________． 考点 双曲线的标准方程题点 由双曲线方程求参数[答案] (2，＋∞)[解析] 由曲线C ：mx 2＋(2－m )y 2＝1是焦点在x 轴上的双曲线，可得x 21m －y 21m －2＝1， 即有m >0，且m －2>0，解得m >2.11．焦点在x 轴上的双曲线经过点P (42，－3)，且Q (0,5)与两焦点的连线互相垂直，则此双曲线的标准方程为______________．考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程[答案] x 216－y 29＝1 [解析] 设焦点F 1(－c,0)，F 2(c,0)(c >0)，则由QF 1⊥QF 2，得1QF k ·2QF k ＝－1， ∴5c ·5－c＝－1，∴c ＝5， 设双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)， ∵双曲线过点(42，－3)，∴32a 2－9b 2＝1， 又∵c 2＝a 2＋b 2＝25，∴a 2＝16，b 2＝9，∴双曲线的标准方程为x 216－y 29＝1. 三、解答题12．已知与双曲线x 216－y 29＝1共焦点的双曲线过点P ⎝⎛⎭⎫－52，－6，求该双曲线的标准方程． 解 已知双曲线x 216－y 29＝1， 则c 2＝16＋9＝25，∴c ＝5.设所求双曲线的标准方程为x 2a 2－y 2b2＝1(a ＞0，b ＞0)． 依题意知b 2＝25－a 2，故所求双曲线方程可写为x 2a 2－y 225－a 2＝1. ∵点P ⎝⎛⎭⎫－52，－6在所求双曲线上， ∴⎝⎛⎭⎫－522a 2－(－6)225－a 2＝1，化简得4a 4－129a 2＋125＝0，解得a 2＝1或a 2＝1254. 当a 2＝1254时，b 2＝25－a 2＝25－1254＝－254＜0， 不合题意，舍去，∴a 2＝1，b 2＝24，∴所求双曲线的标准方程为x 2－y 224＝1. 13．已知双曲线x 216－y 24＝1的左、右焦点分别为F 1，F 2. (1)若点M 在双曲线上，且MF 1→·MF 2→＝0，求M 点到x 轴的距离；(2)若双曲线C 与已知双曲线有相同焦点，且过点(32，2)，求双曲线C 的方程． 考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程解 (1)如图所示，不妨设M 在双曲线的右支上，M 点到x 轴的距离为h ，MF 1→·MF 2→＝0，则MF 1⊥MF 2，设|MF 1|＝m ，|MF 2|＝n ，由双曲线定义，知m －n ＝2a ＝8，①又m 2＋n 2＝(2c )2＝80，②由①②得m ·n ＝8，∴12mn ＝4＝12|F 1F 2|·h ，∴h ＝255.(2)设所求双曲线C 的方程为x 216－λ－y 24＋λ＝1(－4<λ<16)，由于双曲线C 过点(32，2)，∴1816－λ－44＋λ＝1，解得λ＝4或λ＝－14(舍去)，∴所求双曲线C 的方程为x 212－y 28＝1.14．已知F 是双曲线C ：x 2－y 23＝1的右焦点，P 是C 上一点，且PF 与x 轴垂直，点A 的坐标是(1,3)，则△APF 的面积为( )A.13B.12C.23D.32考点 双曲线的定义题点 双曲线的焦点三角形[答案] D[解析] 因为F 是双曲线C ：x 2－y 23＝1的右焦点， 所以F (2,0)．因为PF ⊥x 轴，所以可设P 的坐标为(2，y P )．因为P 是C 上一点，所以4－y 2P 3＝1，解得y P ＝±3， 所以P (2，±3)，|PF |＝3.又因为A (1,3)，所以点A 到直线PF 的距离为1，所以S △APF ＝12×|PF |×1＝12×3×1＝32. 故选D.15．已知△OFQ 的面积为26，且OF →·FQ →＝m ，其中O 为坐标原点．(1)设6<m <46，求OF →与FQ →的夹角θ的正切值的取值范围；(2)设以O 为中心，F 为其中一个焦点的双曲线经过点Q ，如图所示，|OF →|＝c ，m ＝⎝⎛⎭⎫64－1c 2，当|OQ →|取得最小值时，求此双曲线的标准方程．考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程解 (1)因为⎩⎨⎧ 12|OF→|·|FQ →|sin (π－θ)＝26，|OF→|·|FQ →|cos θ＝m ， 所以tan θ＝46m. 又6<m <46，所以1<tan θ<4，即tan θ的取值范围为(1,4)． (2)设双曲线的标准方程为x 2a 2－y 2b2＝1(a >0，b >0)， Q (x 1，y 1)，则FQ →＝(x 1－c ，y 1)，所以S △OFQ ＝12|OF →|·|y 1|＝26，则y 1＝±46c. 又OF →·FQ →＝m ，即(c,0)·(x 1－c ，y 1)＝⎝⎛⎭⎫64－1c 2， 解得x 1＝64c ， 所以|OQ →|＝x 21＋y 21＝38c 2＋96c2≥12＝23，当且仅当c ＝4时，取等号，|OQ →|最小，这时Q 的坐标为(6，6)或(6，－6)．因为⎩⎪⎨⎪⎧ 6a 2－6b 2＝1，a 2＋b 2＝16，所以⎩⎪⎨⎪⎧a 2＝4，b 2＝12， 于是所求双曲线的标准方程为x 24－y 212＝1.。

§ 2.3双曲线2.3.1 双曲线及其标准方程课时目标 1.了解双曲线的定义、几何图形和标准方程的推导过程.2.掌握双曲线的标准方程.3.会利用双曲线的定义和标准方程解决简单的应用问题．1．双曲线的有关概念 (1)双曲线的定义平面内与两个定点F 1，F 2的距离的差的绝对值等于常数(小于________)的点的轨迹叫做双曲线．平面内与两个定点F 1，F 2的距离的差的绝对值等于|F 1F 2|时的点的轨迹为________________________________________________________________________． 平面内与两个定点F 1，F 2的距离的差的绝对值大于|F 1F 2|时的点的轨迹__________． (2)双曲线的焦点和焦距双曲线定义中的两个定点F 1、F 2叫做__________________，两焦点间的距离叫做__________________． 2．双曲线的标准方程(1)焦点在x 轴上的双曲线的标准方程是______________________，焦点F 1__________，F 2__________.(2)焦点在y 轴上的双曲线的标准方程是________________，焦点F 1__________，F 2__________.(3)双曲线中a 、b 、c 的关系是________________．一、选择题1．已知平面上定点F 1、F 2及动点M ，命题甲：||MF 1|－|MF 2||＝2a(a 为常数)，命题乙：M 点轨迹是以F 1、F 2为焦点的双曲线，则甲是乙的( ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 2．若ax 2＋by 2＝b(ab<0)，则这个曲线是( ) A ．双曲线，焦点在x 轴上 B ．双曲线，焦点在y 轴上 C ．椭圆，焦点在x 轴上 D ．椭圆，焦点在y 轴上3．焦点分别为(－2,0)，(2,0)且经过点(2,3)的双曲线的标准方程为( )A ．x 2－y 23＝1 B .x 23－y 2＝1C ．y 2－x 23＝1D .x 22－y 22＝1 4．双曲线x 2m －y23＋m＝1的一个焦点为(2,0)，则m 的值为( )A .12B ．1或3C .1＋22D .2－125．一动圆与两圆：x 2＋y 2＝1和x 2＋y 2－8x ＋12＝0都外切，则动圆圆心的轨迹为( ) A ．抛物线 B ．圆C ．双曲线的一支D ．椭圆6．已知双曲线中心在坐标原点且一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0,2)，则该双曲线的方程是( ) A .x 24－y 2＝1 B ．x 2－y 24＝1 C .x 22－y 23＝1 D .x 23－y22＝1题 号 1 2 3 4 5 6 答 案二、填空题8．已知方程x 21＋k －y 21－k＝1表示双曲线，则k 的取值范围是________．9．F 1、F 2是双曲线x 29－y 216＝1的两个焦点，P 在双曲线上且满足|PF 1|·|PF 2|＝32，则∠F 1PF 2＝________________________________________________________________________. 三、解答题10．设双曲线与椭圆x 227＋y 236＝1有相同的焦点，且与椭圆相交，一个交点A 的纵坐标为4，求此双曲线的标准方程．11．在△ABC 中，B(4,0)、C(－4,0)，动点A 满足sin B －sin C ＝12sin A ，求动点A 的轨迹方程．能力提升A ．[3－23，＋∞)B ．[3＋23，＋∞)C ．[－74，＋∞)D ．[74，＋∞)13．已知双曲线的一个焦点为F(7，0)，直线y ＝x －1与其相交于M ，N 两点，MN 中点的横坐标为－23，求双曲线的标准方程．1．双曲线的标准方程可以通过待定系数法求得．2．和双曲线有关的轨迹问题要按照求轨迹方程的一般步骤来解，也要和双曲线的定义相3．直线和双曲线的交点问题可以转化为解方程组(设而不求)，利用韦达定理，弦长公式等解决．§2.3 双曲线2.3.1 双曲线及其标准方程知识梳理1．(1)|F 1F 2| 以F 1，F 2为端点的两条射线 不存在 (2)双曲线的焦点 双曲线的焦距2．(1)x 2a 2－y 2b 2＝1(a >0，b >0) (－c,0) (c,0)(2)y 2a 2－x 2b2＝1(a >0，b >0) (0，－c ) (0，c ) (3)c 2＝a 2＋b 2 作业设计1．B [根据双曲线的定义，乙⇒甲，但甲 乙， 只有当2a <|F 1F 2|且a ≠0时，其轨迹才是双曲线．]2．B [原方程可化为x 2b a＋y 2＝1，因为ab <0，所以ba <0，所以曲线是焦点在y 轴上的双曲线，故选B.]3．A [∵双曲线的焦点在x 轴上，∴设双曲线方程为x 2a 2－y 2b2＝1 (a >0，b >0)．由题知c ＝2，∴a 2＋b 2＝4.①又点(2,3)在双曲线上，∴22a 2－32b2＝1.②由①②解得a 2＝1，b 2＝3，∴所求双曲线的标准方程为x 2－y 23＝1.]4．A [∵双曲线的焦点为(2,0)，在x 轴上且c ＝2，∴m ＋3＋m ＝c 2＝4.∴m ＝12.]5．C [由题意两定圆的圆心坐标为O 1(0,0)，O 2(4,0)，设动圆圆心为O ，动圆半径为r ，则|OO 1|＝r ＋1，|OO 2|＝r ＋2，∴|OO 2|－|OO 1|＝1<|O 1O 2|＝4，故动圆圆心的轨迹为双曲线的一支．]6．B [设双曲线方程为x 2a 2－y 2b 2＝1，因为c ＝5，c 2＝a 2＋b 2，所以b 2＝5－a 2，所以x 2a 2－y 25－a 2＝1.由于线段PF 1的中点坐标为(0,2)，则P 点的坐标为(5，4)．代入双曲线方程得5a 2－165－a 2＝1，解得a 2＝1或a 2＝25(舍去)，所以双曲线方程为x 2－y 24＝1.故选B.]7．2解析 ∵||PF 1|－|PF 2||＝4，又PF 1⊥PF 2，|F 1F 2|＝25， ∴|PF 1|2＋|PF 2|2＝20，∴(|PF 1|－|PF 2|)2 ＝20－2|PF 1||PF 2|＝16，∴|PF 1|·|PF 2|＝2. 8．－1<k <1解析 因为方程x 21＋k －y 21－k＝1表示双曲线，所以(1＋k )(1－k )>0.所以(k ＋1)(k －1)<0. 所以－1<k <1.解析 设∠F 1PF 2＝α，|PF 1|＝r 1，|PF 2|＝r 2. 在△F 1PF 2中，由余弦定理，得(2c )2＝r 21＋r 22－2r 1r 2cos α，∴cos α＝(r 1－r 2)2＋2r 1r 2－4c 22r 1r 2＝36＋64－10064＝0.∴α＝90°.10．解 方法一 设双曲线的标准方程为y 2a 2－x 2b2＝1 (a >0，b >0)，由题意知c 2＝36－27＝9，c ＝3.又点A 的纵坐标为4，则横坐标为±15，于是有 ⎩⎪⎨⎪⎧42a 2－(±15)2b 2＝1，a 2＋b 2＝9，解得⎩⎪⎨⎪⎧a 2＝4，b 2＝5.所以双曲线的标准方程为y 24－x 25＝1.方法二 将点A 的纵坐标代入椭圆方程得A (±15，4)， 又两焦点分别为F 1(0,3)，F 2(0，－3)． 所以2a ＝|(±15－0)2＋(4＋3)2－(±15－0)2＋(4－3)2|＝4， 即a ＝2，b 2＝c 2－a 2＝9－4＝5，所以双曲线的标准方程为y 24－x 25＝1.11．解 设A 点的坐标为(x ，y )，在△ABC 中，由正弦定理，得a sin A ＝b sin B ＝c sin C ＝2R ，代入sin B －sin C ＝12sin A ， 得|AC |2R －|AB |2R ＝12·|BC |2R ，又|BC |＝8， 所以|AC |－|AB |＝4.因此A 点的轨迹是以B 、C 为焦点的双曲线的右支(除去右顶点)且2a ＝4,2c ＝8，所以a ＝2，c ＝4，b 2＝12.所以A 点的轨迹方程为x 24－y 212＝1 (x >2)．12．B[由c ＝2得a 2＋1＝4，∴a 2＝3，∴双曲线方程为x 23－y 2＝1.设P (x ，y )(x ≥3)，13．解 设双曲线的标准方程为x 2a 2－y 2b2＝1，且c ＝7，则a 2＋b 2＝7.①由MN 中点的横坐标为－23知，中点坐标为⎝⎛⎭⎫－23，－53. 设M (x 1，y 1)，N (x 2，y 2)，则由⎩⎨⎧x 21a 2－y 21b 2＝1，x 22a 2－y 22b 2＝1，得b 2(x 1＋x 2)(x 1－x 2)－a 2(y 1＋y 2)(y 1－y 2)＝0.∵⎩⎨⎧x 1＋x 2＝－43y 1＋y 2＝－103，且y 1－y 2x 1－x 2＝1，∴2b 2＝5a 2.②由①，②求得a 2＝2，b 2＝5.∴所求双曲线的标准方程为x 22－y 25＝1.小课堂：如何培养中学生的自主学习能力？自主学习是与传统的接受学习相对应的一种现代化学习方式。

第二章 2.3 课时作业17一、选择题1．双曲线x 210－y 22＝1的焦距为( )A ．32B ．4 2C ．33D ．4 3解析：由双曲线的标准方程可知，a 2＝10，b 2＝2.于是有c 2＝a 2＋b 2＝12，则2c ＝4 3.故选D.答案：D2．已知双曲线的a ＝5，c ＝7，则该双曲线的标准方程为( ) A.x 225－y 224＝1 B.y 225－x 224＝1 C.x 225－y 224＝1或y 225－x 224＝1 D.x 225－y 249＝1或y 225－x 249＝1 解析：因为b 2＝c 2－a 2＝49－25＝24，且焦点位置不确定，所以所求双曲线的标准方程为x 225－y 224＝1或y 225－x 224＝1. 答案：C3．[2014·福建宁德一模]已知椭圆x 2a 2＋y 29＝1(a >0)与双曲线x 24－y 23＝1有相同的焦点，则a的值为( )A. 2B. 10C. 4D. 34解析：因为椭圆x 2a 2＋y 29＝1(a >0)与双曲线x 24－y 23＝1有相同的焦点(±7，0)，则有a 2－9＝7，∴a ＝4.选C.答案：C4．已知双曲线中心在坐标原点且一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0,2)，则该双曲线的方程是( )A.x 24－y 2＝1 B ．x 2－y 24＝1C.x 22－y 23＝1 D.x 23－y 22＝1 解析：设双曲线方程为x 2a 2－y 2b 2＝1，因为c ＝5，c 2＝a 2＋b 2，所以b 2＝5－a 2，所以x 2a 2－y 25－a 2＝1.由于线段PF 1的中点坐标为(0,2)，则P 点的坐标为(5，4)．代入双曲线方程得5a 2－165－a 2＝1，解得a 2＝1或a 2＝25(舍去)，所以双曲线方程为x 2－y 24＝1.故选B.答案：B 二、填空题5．设m 是常数，若点F (0,5)是双曲线y 2m －x 29＝1的一个焦点，则m ＝__________.解析：由点F (0,5)可知该双曲线y 2m －x 29＝1的焦点落在y 轴上，所以m >0，且m ＋9＝52，解得m ＝16.答案：166．已知P 是双曲线x 264－y 236＝1上一点，F 1，F 2是双曲线的两个焦点，若|PF 1|＝17，则|PF 2|的值为__________．解析：由双曲线方程x 264－y 236＝1知，a ＝8，b ＝6，则c ＝a 2＋b 2＝10.∵P 是双曲线上一点，∴||PF 1|－|PF 2||＝2a ＝16，又|PF 1|＝17，∴|PF 2|＝1或|PF 2|＝33. 又|PF 2|≥c －a ＝2，∴|PF 2|＝33. 答案：337．在△ABC 中，B (－6,0)，C (6,0)，直线AB ，AC 的斜率乘积为94，则顶点A 的轨迹方程为__________．解析：设顶点A 的坐标为(x ，y )，根据题意，得y x ＋6·y x －6＝94，化简，得x 236－y 281＝1(x ≠±6)．故填x 236－y 281＝1(x ≠±6)． 答案：x 236－y 281＝1(x ≠±6)三、解答题8．求适合下列条件的双曲线的标准方程：(1)以椭圆x 225＋y 29＝1的长轴端点为焦点，且经过点P (5，94)；(2)过点P 1(3，－42)，P 2(94，5)．解：(1)因为椭圆x 225＋y 29＝1的长轴端点为A 1(－5,0)，A 2(5,0)，所以所求双曲线的焦点为F 1(－5,0)，F 2(5,0)．由双曲线的定义知，||PF 1|－|PF 2|| ＝⎪⎪⎪⎪(5＋5)2＋(94－0)2－(5－5)2＋(94－0)2 ＝⎪⎪⎪⎪(414)2－(94)2＝8，即2a ＝8，则a ＝4. 又c ＝5，所以b 2＝c 2－a 2＝9.故所求双曲线的标准方程为x 216－y 29＝1.(2)设双曲线的方程为Ax 2＋By 2＝1(AB <0)，分别将点P 1(3，－42)，P 2(94，5)代入，得⎩⎪⎨⎪⎧9A ＋32B ＝18116A ＋25B ＝1，解得⎩⎨⎧A ＝－19B ＝116，故所求双曲线的标准方程为y 216－x 29＝1.9．已知曲线x 216－m －y 2m＝1.(1)当曲线是椭圆时，求实数m 的取值范围，并写出焦点坐标； (2)当曲线是双曲线时，求实数m 的取值范围，并写出焦点坐标． 解：(1)曲线为椭圆⇔⎩⎪⎨⎪⎧16－m >0－m >016－m ≠－m⇔⎩⎨⎧m <16m <0⇔m <0.即实数m 的取值范围是(－∞，0)．此时，椭圆的焦点在x 轴上，坐标为(±4,0)．(2)曲线为双曲线⇔(16－m )m >0⇔0<m <16.即实数m 的取值范围是(0,16)． 此时，双曲线的焦点在x 轴上，坐标为(±4,0)．。

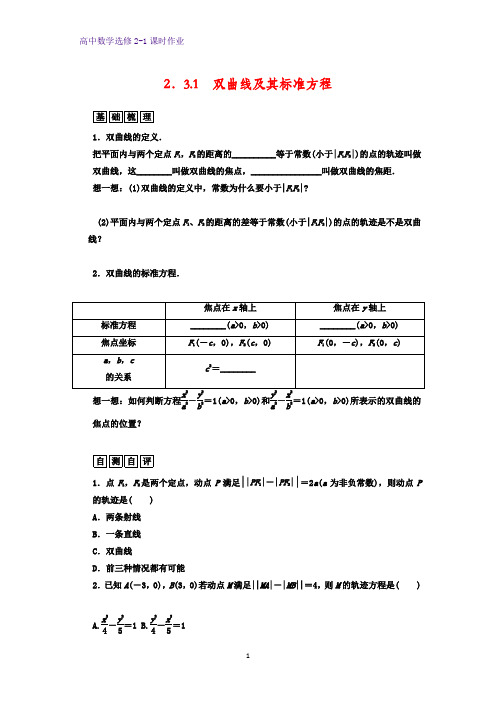
2．3.1 双曲线及其标准方程基础梳理1．双曲线的定义．把平面内与两个定点F1，F2的距离的__________等于常数(小于|F1F2|)的点的轨迹叫做双曲线，这________叫做双曲线的焦点，________________叫做双曲线的焦距．想一想：(1)双曲线的定义中，常数为什么要小于|F1F2|?(2)平面内与两个定点F1、F2的距离的差等于常数(小于|F1F2|)的点的轨迹是不是双曲线？2．双曲线的标准方程．想一想：如何判断方程a2－b2＝1(a>0，b>0)和a2－b2＝1(a>0，b>0)所表示的双曲线的焦点的位置？自测自评1．点F1，F2是两个定点，动点P满足|||PF1|－|PF2|＝2a(a为非负常数)，则动点P 的轨迹是( )A．两条射线B．一条直线C．双曲线D．前三种情况都有可能2．已知A(－3，0)，B(3，0)若动点M满足||MA|－|MB||＝4，则M的轨迹方程是( )A.x24－y25＝1 B.y24－x25＝1C.x 29－y 25＝1D.y 29－x 25＝1 3．若方程x 2m －1＋y 2m 2－4＝3表示焦点在y 轴上的双曲线，则m 的取值范围是( )A ．1＜m ＜2B ．m ＞2C ．m ＜－2D ．－2＜m ＜2基础巩固1．若动点P 到F 1(－5，0)与P 到F 2(5，0)的距离的差为±8，则P 点的轨迹方程是( ) A.x 225＋y 216＝1 B.x 225－y 216＝1 C.x 216＋y 29＝1 D.x 216－y 29＝1 2．已知F 1(－5，0)，F 2(5，0)为定点，动点P 满足|PF 1|－|PF 2|＝2a ，当a ＝3和a ＝5时，P 点的轨迹分别为( )A ．双曲线和一条直线B ．双曲线的一支和一条直线C ．双曲线和一条射线D ．双曲线的一支和一条射线3．椭圆x 24＋y 2a 2＝1与双曲线x 2a －y 22＝1有相同的焦点，则a 的值是( ) A ．2 B ．1 C. 2 D ．34．若曲线x 2k ＋y 2k －1＝1表示双曲线，则k 的取值范围是____________． 能力提升5．已知双曲线的中心在原点且一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0，2)，则双曲线的方程是( )A.x 24－y 2＝1 B ．x 2－y 24＝1 C.x 22－y 23＝1 D.x 23－y 22＝1 6．若k >1，则关于x ，y 的方程(1－k )x 2＋y 2＝k 2－1所表示的曲线是( )A ．焦点在x 轴上的椭圆B ．焦点在y 轴上的椭圆C．焦点在y轴上的双曲线D．焦点在x轴上的双曲线7．F1、F2是双曲线y29－x216＝1的两个焦点，M是双曲线上一点，且|MF1|·|MF2|＝32，则△F1MF2的面积为________．8．已知双曲线的方程是x216－y28＝1，点P在双曲线上，且到其中一个焦点F1的距离为10，点N是PF1的中点，则|ON|的大小(O为坐标原点)为________________．9．相距1 400 m的两个哨所，听到炮弹爆炸声的时间相差3 s，已知声速是340 m/s，建立直角坐标系，求出炮弹爆炸点所在的曲线方程．10．如图，圆E：(x＋2)2＋y2＝4，点F(2，0)，动圆P过点F，且与圆E内切于点M，求动圆P的圆心P的轨迹方程．答 案基础梳理1．差的绝对值 两个定点 两焦点间的距离想一想：[解析](1)①如果定义中常数改为等于|F 1F 2|，此时动点的轨迹是以F 1、F 2为端点的两条射线(包括端点)．②如果定义中常数为0，此时动点轨迹为线段F 1F 2的垂直平分线．③如果定义中常数改为大于|F 1F 2|，此时动点轨迹不存在．(2)不是，是双曲线的某一支．在双曲线的定义中，P 为动点，F 1，F 2分别为双曲线的左、右焦点，则①|PF 1|－|PF 2|＝2a ，曲线只表示双曲线的右支．②|PF 1|－|PF 2|＝－2a ，曲线只表示双曲线的左支．2.x 2a 2－y 2b 2＝1 y 2a 2－x 2b 2＝1 a 2＋b 2 想一想：[解析]在x 2，y 2的系数异号的前提下，如果x 2项的系数是正的，那么焦点在x 轴上，如果y 2项的系数是正的，那么焦点在y 轴上．对于双曲线，a 不一定大于b ，因此，不能像椭圆那样用比较分母的大小来判定焦点在哪一个坐标轴上．自测自评1．[答案]D2．[解析]根据双曲线的定义知，动点M 的轨迹是双曲线，焦点在x 轴上，a ＝2，c ＝3，所以b 2＝5.所以轨迹方程为x 24－y 25＝1.故选A. [答案]A3．[解析]由⎩⎪⎨⎪⎧m 2－4＞0，m －1＜0得m ＜－2. [答案]C基础巩固1．[解析]由双曲线定义知：2a ＝8，∴a ＝4，c ＝5，∴b ＝3.[答案]D2．[解析]∵|F 1F 2|＝10，|PF 1|－|PF 2|＝2a ，∴当a ＝3时，2a ＝6＜|F 1F 2|，为双曲线的一支；当a ＝5时，2a ＝10＝|F 1F 2|，为一条射线．[答案]D3．[解析]∵双曲线的标准方程为x 2a －y 22＝1，∴a >0，焦点在x 轴上，∴a ＋2＝4－a 2， 即a 2＋a －2＝0，解得a ＝1，a ＝－2(舍去)．∴a ＝1.[答案]B4．[解析]只要k (k －1)＜0即可．[答案](0，1)能力提升5．[解析]由题意知双曲线的焦点在x 轴，且另一焦点为F 2(5，0)，又由中点坐标公式求得P 点坐标为(5，4)，则|PF 1|＝6，|PF 2|＝4.∴|PF 1|－|PF 2|＝2a ＝6－4＝2＜2 5.[答案]B6．[解析]将已知方程化为标准形式，根据项的系数符号进行判断．原方程可化为y 2k 2－1－x 21＋k ＝1.∵k >1，∴k 2－1>0，1＋k >0.∴已知方程表示的曲线为焦点在y 轴上的双曲线．[答案]C7．[解析]由题意可得双曲线的两个焦点是F 1(0，－5)、F 2(0，5)，由双曲线定义得，||MF 1|－|MF 2||＝6，联立|MF 1|·|MF 2|＝32，得|MF 1|2＋|MF 2|2＝100＝|F 1F 2|2，所以△F 1MF 2是直角三角形，从而其面积为S ＝12|MF 1|·|MF 2|＝16. [答案]168．[解析]设双曲线的另一个焦点为F 2，连接PF 2，ON 是三角形PF 1F 2的中位线，所以|ON |＝12|PF 2|，因为||PF 1|－|PF 2||＝8，|PF 1|＝10，所以|PF 2|＝2或18，所以|ON |＝12|PF 2|＝1或9.[答案]1或99．[答案]解：以两个哨所(设为A 、B )的连线为x 轴，两个哨所连线的中点为原点，建立直角坐标系，设爆炸点为P ，由已知，可得||PA |－|PB ||＝3×340＝1 020，所以点P 的轨迹是双曲线，根据已知，c ＝700，a ＝510，所以b 2＝c 2－a 2＝229 900， 所以，所求轨迹方程为x 2260 100－y 2229 900＝1.10．[答案]解：由已知，圆E半径为r＝2，设圆P的半径为R，则|PF|＝|PM|＝R，|ME|＝r＝2，|PE|＝|PM|－|ME|＝R－2，所以|PF|－|PE|＝2，由双曲线的定义知，P的轨迹为双曲线的左支，因为a＝1，c＝2，所以b＝3，所以，所求轨迹方程为x2－y23＝1(x≤－1)．。

双曲线及其标准方程导学案【学习要求】1．了解双曲线的定义，几何图形和标准方程的推导过程. 2．掌握双曲线的标准方程.3．会利用双曲线的定义和标准方程解决简单的问题.【学法指导】本节课的学习要运用类比的方法，在与椭圆的联系与区别中建立双曲线的定义及标准方程.【知识要点】1．双曲线的定义把平面内与两个定点F 1，F 2的距离的 等于常数(小于|F 1F 2|)的点的轨迹叫做双曲线，这两个定点叫做 ， 叫做双曲线的焦距. 2探究点一 双曲线的定义问题1 取一条拉链，拉开它的一部分，在拉开的两边上各选择一点，分别固定在点F 1，F 2上，把笔尖放在点M 处，拉开闭拢拉链，笔尖经过的点可画出一条曲线，思考曲线满足什么条件？问题2 双曲线的定义中强调平面内动点到两定点的距离差的绝对值为常数，若没有绝对值，则动点的轨迹是什么？问题3 双曲线的定义中，为什么要限制到两定点距离之差的绝对值为常数2a,2a <|F 1F 2|?问题4 已知点P (x ，y )的坐标满足下列条件，试判断下列各条件下点P 的轨迹是什么图形？ （1）6)5()5(2222=+--++y x y x ；（2）6)4()4(2222=+--++y x y x（3）方程x ＝3y 2－1所表示的曲线是( )A ．双曲线B ．椭圆C ．双曲线的一部分D ．椭圆的一部分 探究点二 双曲线的标准方程问题1 类比椭圆的标准方程推导过程，思考怎样求双曲线的标准方程？问题2 两种形式的标准方程怎样进行区别？能否统一？问题3 如图，类比椭圆中a ，b ，c 的意义，你能在y 轴上找一点B ，使|OB |＝b 吗？例1 （1）已知双曲线的焦点在y 轴上，并且双曲线过点(3，－42)和⎝⎛⎭⎫94，5，求双曲线的标准方程； （2）求与双曲线x 216－y 24＝1有公共焦点，且过点(32，2)的双曲线方程.跟踪训练1 （1）过点(1,1)且ba＝2的双曲线的标准方程是 ( )A ．12122=-y x B ．y 212－x 2＝1 C ．x 2－y 212＝1D ．x 212－y 2＝1或y 212－x 2＝1（2）若双曲线以椭圆x 216＋y 29＝1的两个顶点为焦点，且经过椭圆的两个焦点，则双曲线的标准方程为_______探究点三 与双曲线定义有关的应用问题例2 已知双曲线的方程是x 216－y 28＝1，点P 在双曲线上，且到其中一个焦点F 1的距离为10，点N 是PF 1的中点，求|ON |的大小(O 为坐标原点).跟踪训练2 如图，从双曲线x 23－y 25＝1的左焦点F 引圆x 2＋y 2＝3的切线FP 交双曲线右支于点P ， T 为切点，M 为线段FP 的中点，O 为坐标原点，则|MO |－|MT |等于( )A ． 3B ． 5C ．5－ 3D ．5＋ 3例3 已知A ，B 两地相距800 m ，在A 地听到炮弹爆炸声比在B 地晚2 s ，且声速为340 m/s ，求炮弹爆炸点的轨迹方程.跟踪训练3 2008年5月12日，四川汶川发生里氏8.0级地震，为了援救灾民，某部队在如图所示的P 处空降了一批救灾药品，今要把这批药品沿道路PA 、PB 送到矩形灾民区ABCD 中去，已知PA ＝100 km ，PB ＝150 km ，BC ＝60 km ，∠APB ＝60°，试在灾民区中确定一条界线，使位于界线一侧的点沿道路PA 送药较近，而另一侧的点沿道路PB 送药较近，请说明这一界线是一条什么曲线？并求出其方程.【当堂检测】1．已知A (0，－5)、B (0,5)，|PA |－|PB |＝2a ，当a ＝3或5时，P 点的轨迹为 ( ) A ．双曲线或一条直线 B ．双曲线或两条直线 C ．双曲线一支或一条直线 D ．双曲线一支或一条射线2．若k >1，则关于x ，y 的方程(1－k )x 2＋y 2＝k 2－1所表示的曲线是 ( ) A ．焦点在x 轴上的椭圆 B ．焦点在y 轴上的椭圆 C ．焦点在y 轴上的双曲线 D ．焦点在x 轴上的双曲线 3．双曲线x 216－y 29＝1上一点P 到点(5,0)的距离为15，那么该点到(－5,0)的距离为 ( )A ．7B ．23C ．5或25D ．7或234．已知动圆M 与圆C 1：(x ＋4)2＋y 2＝2外切，与圆C 2：(x －4)2＋y 2＝2内切，求动圆圆心的轨迹方程.【课堂小结】1．双曲线定义中||PF 1|－|PF 2||＝2a (2a <|F 1F 2|)不要漏了绝对值符号，当2a ＝|F 1F 2|时表示两条射线.2．在双曲线的标准方程中，a >b 不一定成立.要注意与椭圆中a ，b ，c 的区别.在椭圆中a 2＝b 2＋c 2，在双曲线中c 2＝a 2＋b 2.3．用待定系数法求双曲线的标准方程时，要先判断焦点所在的位置，设出标准方程后，由条件列出a ，b ，c 的方程组.如果焦点不确定要分类讨论，采用待定系数法求方程或用形如mx 2＋ny 2＝1 (mn <0)的形式求解.【拓展提高】1．已知方程12522=---k y k x 的图形是双曲线，那么k 的取值范围是（ ）A ．k >5B ．k >5，或22<<-kC ．k >2,，或2-<kD ．22<<-k2．===-212221121625,PF PF y x F F P ，则上一点，且为焦点的双曲线是以点（ ） A ．2 B ．22 C ．4或22 D ．2或223．已知双曲线14922=-y x ，B A 、为过左焦点1F 的直线与双曲线左支的两个交点，2,9F AB =为右焦点，则△B AF 2的周长为4．是双曲线上的一点，且，点的两个焦点分别是已知双曲线P F F y x 2122,13=-__________602121的面积等于，则PF F PF F ∆=∠5．根据下列条件，求双曲线的标准方程． （1）过点P )415,3(，Q )5,316(-且焦点在坐标轴上； （2）c ＝6，经过点(－5,2)，焦点在x 轴上．（3））的双曲线。

选修2-1双曲线及其标准方程课时作业work Information Technology Company.2020YEAR课时作业11 双曲线及其标准方程时间：45分钟 满分：100分一、选择题(每小题5分，共30分) 1．双曲线x 216－y 29＝1的焦点坐标为( ) A ．(－7，0)，(7，0) B ．(0，－7)，(0，7) C ．(－5,0)，(5,0) D ．(0，－5)，(0,5)【答案】 C【解析】 ∵a 2＝16，b 2＝9，∴c 2＝a 2＋b 2＝25，∴c ＝5，又焦点在x 轴上，所以焦点坐标为(5,0)和(－5,0)．故选C.2．设动点M 到A (－5,0)的距离与它到B (5,0)的距离的差等于6，则P 点的轨迹方程是( )A.x 29－y 216＝1 B.y 29－x 216＝1 C.x 29－y 216＝1(x ≤－3) D.x 29－y 216＝1(x ≥3) 【答案】 D【解析】 由题意得点M 到A 点的距离大于到B 点的距离，且|MA |－|MB |<10，所以动点M 的轨迹是双曲线的右支．3．已知定点A ，B ，且|AB |＝4，动点P 满足|P A |－|PB |＝3，则|P A |的最小值为( )A.12B.32C.72D ．5【答案】 C 【解析】点P 的轨迹是以A ，B 为焦点的双曲线的右支，如右图所示，当P 与双曲线右支顶点M 重合时，|P A |最小，最小值为a ＋c ＝32＋2＝72，故选C.4．已知点F 1(－2，0)、F 2(2，0)，动点P 满足|PF 2|－|PF 1|＝2.当点P 的纵坐标是12时，点P 到坐标原点的距离是( )A.62B.32C. 3 D ．2【答案】 A【解析】 由题意知，点P 的轨迹是双曲线的左支，c ＝2，a ＝1，b ＝1，∴双曲线的方程为x 2－y 2＝1，把y ＝12代入双曲线方程，得x 2＝1＋14＝54.∴|OP |2＝x 2＋y 2＝54＋14＝64，∴|OP |＝62.5．已知双曲线x 29－y 216＝1上一点P 到焦点F 1的距离为8，则P 到焦点F 2的距离为( )A ．2B ．2或14C ．14D ．16【答案】 B 【解析】 如图，设F 1、F 2分别是双曲线的左、右焦点， 由已知得a ＝3，b ＝4，c ＝5，∵双曲线右顶点到左焦点F 1的距离为a ＋c ＝8， ∴点P 在双曲线右顶点时，|PF 2|＝c －a ＝5－3＝2， 当点P 在双曲线左支上时，|PF 2|－|PF 1|＝2a ＝6， ∴|PF 2|＝|PF 1|＋6＝8＋6＝14.6．设F 1、F 2为双曲线x 25－y 24＝1的两个焦点，P (3,1)是双曲线内的一点，点A 是双曲线上一动点，则|AP |＋|AF 2|的最小值为( )A.37＋4B.37－4C.37－2 5D.37＋2 5 【答案】 C【解析】 如图，连接F 1P 交双曲线右支于点A 0，∵|AP |＋|AF 2|＝|AP |＋|AF 1|－25，∴要求|AP |＋|AF 2|的最小值，只需求|AP |＋|AF 1|的最小值，当A 落在A 0时，|AP |＋|AF 1|＝|PF 1|最小，最小值为37，∴|AP |＋|AF 2|的最小值为37－2 5.二、填空题(每小题10分，共30分)7．已知双曲线C ：x 29－y 216＝1的左、右焦点分别为F 1、F 2，P 为双曲线C 的右支上一点，且|PF 2|＝|F 1F 2|，则△PF 1F 2的面积等于________．【答案】 48【解析】 由题意知|F 1F 2|＝|PF 2|＝10且|PF 1|－|PF 2|＝6.∴|PF 1|＝16.由勾股定理得PF 1上的高h ＝102－82＝6.∴△PF 1F 2的面积S ＝12h ·|PF 1|＝12×6×16＝48.8．已知双曲线的一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0,2)，则该双曲线的标准方程是________.【答案】 x 2－y24＝1【解析】 因为线段PF 1的中点坐标为(0,2)，所以P 点坐标为(5，4)，又因为焦点在x 轴上，且c ＝5，所以设双曲线的标准方程为x 2a 2－y 25－a 2＝1，将(5，4)代入得5a 2－165－a 2＝1，解得a 2＝25或a 2＝1，由c >a 知a ＝1，此时b 2＝c 2－a 2＝4，所以双曲线的标准方程为x 2－y24＝1.9．过双曲线x 23－y 24＝1的焦点且与x 轴垂直的弦的长度为________．【答案】 833【解析】 ∵a 2＝3，b 2＝4，∴c 2＝7， ∴c ＝7，弦所在直线方程为x ＝7，由⎩⎪⎨⎪⎧x ＝7x 23－y 24＝1得y 2＝163，∴|y |＝433，弦长为833.三、解答题(本题共3小题，共40分．解答应写出必要的文字说明、证明过程或演算步骤)10．(13分)双曲线x 29－y 216＝1的两个焦点为F 1、F 2，点P 是双曲线上的点．若PF 1⊥PF 2，则点P 到x 轴的距离是多少？【解析】 解法一：由题意得F 1(－5,0)、F 2(5,0)， 设P 的坐标是(x 0，y 0)，又PF 1⊥PF 2， 则|PF 1|2＋|PF 2|2＝|F 1F 2|2，∴⎩⎪⎨⎪⎧(x 0＋5)2＋y 20＋(x 0－5)2＋y 20＝100，x 209－y 2016＝1.解得|y 0|＝165，∴P 到x 轴的距离为165.解法二：以O 为圆心，以|F 1F 2|2＝5为半径作圆x 2＋y 2＝25，与x 29－y 216＝1联立得⎩⎪⎨⎪⎧x 2＋y 2＝25，x 29－y 216＝1，解得y 2＝16225，即|y |＝165.∴P 到x 轴的距离为165.11．(13分)已知x 21－k －y 2|k |－3＝－1，求当k 为何值时：①方程表示双曲线；②方程表示焦点在x 轴上的双曲线；③方程表示焦点在y 轴上的双曲线．【分析】 求参数的值或范围时，可先根据焦点的位置把方程化为相应的标准方程的形式，再根据其余条件确定方程中的a 2，b 2.【解析】 ①若方程表示双曲线，则需满足：⎩⎨⎧1－k >0|k |－3>0或⎩⎨⎧1－k <0，|k |－3<0，解得k <－3或1<k <3.②若方程表示焦点在x 轴上的双曲线，则1<k <3. ③若方程表示焦点在y 轴上的双曲线，则k <－3.【总结】 明确方程Ax 2＋By 2＝C 表示双曲线的条件，即AB <0，且C ≠0.化成x 2C A ＋y 2C B ＝1的形式，若焦点在x 轴上，则C A >0，CB<0；若焦点在y 轴上，则C B >0，CA <0.12．(14分)已知定点A (0,7)、B (0，－7)、C (12,2)，以C 为一个焦点作过A 、B 的椭圆，求椭圆的另一焦点F 的轨迹方程．【解析】 设F (x ，y )为轨迹上的任意一点， 因为A 、B 两点在以C 、F 为焦点的椭圆上，所以|F A |＋|CA |＝2a ，|FB |＋|CB |＝2a (其中a 表示椭圆的长半轴长)，所以|F A |＋|CA |＝|FB |＋|CB |， 所以|F A |－|FB |＝|CB |－|CA |＝122＋92－122＋52＝2.所以|F A |－|FB |＝2.由双曲线的定义知，F 点在以A 、B 为焦点的双曲线的下半支上，所以点F的轨迹方程是y2－x2＝1(y≤－1)．48。

2.2.1双曲线及其标准方程课时作业高二上学期数学北师大版（2019）选择性必修第一册（含答案）2.1 双曲线及其标准方程1.双曲线方程为x2-2y2=1,则它的右焦点坐标为()A.22,0B.62,0C.52,0D.(3,0)2.已知双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,若|PF1|-|PF2|=b,且双曲线的焦距为25,则该双曲线的方程为()A.x24-y2=1B.x23-y22=1C.x2-y24=1D.x22-y23=13.已知双曲线x2λ-3+y22-λ=1,焦点在y轴上,若焦距为4,则λ等于()A.32B.5C.7D.124.已知双曲线x24-y25=1上一点P到左焦点F1的距离为10,则PF1的中点N到坐标原点O的距离为()A.3或7B.6或14C.3D.75.如图,已知双曲线的方程为x2a2-y2b2=1(a>0,b>0),点A,B均在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为双曲线的左焦点,则△ABF1的周长为()A.2a+2mB.4a+2mC.a+mD.2a+4m6.与圆x2+y2=1及圆x2+y2-8x+12=0都外切的圆P的圆心在()A.一个椭圆上B.一个圆上C.一条抛物线上D.双曲线的一支上7.以椭圆x23+y24=1的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线的标准方程是.8.已知点F1,F2分别是双曲线x29-y216=1的左、右焦点,若点P是双曲线左支上的点,且|PF1|·|PF2|=32,则△F1PF2的面积为.9.已知与双曲线x216-y29=1共焦点的双曲线过点P-52,-6,求该双曲线的标准方程.能力达标10.“mn<0”是方程“mx2+ny2=1表示双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件11.已知平面内两定点A(-5,0),B(5,0),动点M满足|MA|-|MB|=6,则点M的轨迹方程是()A.x216-y29=1B.x216-y29=1(x≥4)C.x29-y216=1D.x29-y216=1(x≥3)12.动圆与圆x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹是()A.双曲线的一支B.圆C.椭圆D.双曲线13.若双曲线x2n-y2=1(n>1)的左、右焦点分别为F1,F2,点P在双曲线上,且满足|PF1|+|PF2|=2n+2,则△PF1F2的面积为()A.1B.12C.2D.414.已知左、右焦点分别为F1,F2的双曲线C:x2a2-y2=1(a>0)过点15,-63,点P在双曲线C上,若|PF1|=3,则|PF2|=()A.3B.6C.9D.1215.若曲线C:mx2+(2-m)y2=1是焦点在x轴上的双曲线,则m的取值范围为.16.焦点在x轴上的双曲线经过点(42,-3),且Q(0,5)与两焦点的连线互相垂直,则此双曲线的标准方程为.17.已知双曲线E:x216-y24=1的左、右焦点分别为F1,F2.(1)若点M在双曲线上,且MF1·MF2=0,求点M到x轴的距离;(2)若双曲线C与双曲线E有相同的焦点,且过点(32,2),求双曲线C 的方程.18.已知△OFQ的面积为26,且OF·FQ=m,其中O为坐标原点.(1)设6(2)设以O为中心,F为其中一个焦点的双曲线经过点Q,如图所示,|OF|=c,m=64-1c2,当|OQ|取得最小值时,求此双曲线的标准方程.1.双曲线方程为x2-2y2=1,则它的右焦点坐标为()A.22,0B.62,0C.52,0D.(3,0)答案B解析将双曲线方程化为标准方程为x2-y212=1,∴a2=1,b2=12,∴c2=a2+b2=32,∴c=62,故右焦点坐标为62,0.2.已知双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,若|PF1|-|PF2|=b,且双曲线的焦距为25,则该双曲线的方程为()A.x24-y2=1B.x23-y22=1C.x2-y24=1D.x22-y23=1答案C解析由题意得|PF1|-|PF2|=2a=b,c2=a2+b2,2c=25,解得a2=1,b2=4,则该双曲线的方程为x2-y24=1.3.已知双曲线x2λ-3+y22-λ=1,焦点在y轴上,若焦距为4,则λ等于()A.32B.5C.7D.12答案D解析根据题意可知,双曲线的标准方程为y22-λ-x23-λ=1.由其焦距为4,得c=2,则有c2=2-λ+3-λ=4,解得λ=12.4.已知双曲线x24-y25=1上一点P到左焦点F1的距离为10,则PF1的中点N到坐标原点O的距离为()A.3或7B.6或14C.3D.7答案A解析连接ON,ON是△PF1F2的中位线,∴|ON|=12|PF2|,∵||PF1|-|PF2||=4,|PF1|=10,∴|PF2|=14或|PF2|=6,∴|ON|=7或|ON|=3.5.如图,已知双曲线的方程为x2a2-y2b2=1(a>0,b>0),点A,B均在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为双曲线的左焦点,则△ABF1的周长为()A.2a+2mB.4a+2mC.a+mD.2a+4m答案B解析由双曲线的定义,知|AF1|-|AF2|=2a,|BF1|-|BF2|=2a.又|AF2|+|BF2|=|AB|,所以△ABF1的周长为|AF1|+|BF1|+|AB|=4a+2|AB|=4a+2m.6.与圆x2+y2=1及圆x2+y2-8x+12=0都外切的圆P的圆心在()A.一个椭圆上B.一个圆上C.一条抛物线上D.双曲线的一支上答案D解析由x2+y2-8x+12=0,得(x-4)2+y2=4,画出圆x2+y2=1与(x-4)2+y2=4的图象如图,设圆P的半径为r,∵圆P与圆O和圆M都外切,∴|PM|=r+2,|PO|=r+1,则|PM|-|PO|=1<4,∴点P在以O,M为焦点的双曲线的左支上.7.以椭圆x23+y24=1的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线的标准方程是.答案y2-x23=1 解析由题意知,双曲线的焦点在y轴上,设双曲线的标准方程为y2a2-x2b2=1,则a=1,c=2,所以b2=3,所以双曲线的标准方程为y2-x23=1.8.已知点F1,F2分别是双曲线x29-y216=1的左、右焦点,若点P是双曲线左支上的点,且|PF1|·|PF2|=32,则△F1PF2的面积为.答案16 解析因为P是双曲线左支上的点,所以|PF2|-|PF1|=6,两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,所以|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.在△F1PF2中,由余弦定理,得cos∠F1PF2=|PF1|2+|PF2|2-|F1F2|22|PF1|·|PF2|=100-1002|PF1|·|PF2|=0,所以∠F1PF2=90°,所以S△F1PF2=12|PF1|·|PF2|=12×32=16.9.已知与双曲线x216-y29=1共焦点的双曲线过点P-52,-6,求该双曲线的标准方程.解已知双曲线x216-y29=1,则c2=16+9=25,∴c=5.设所求双曲线的标准方程为x2a2-y2b2=1(a>0,b>0).依题意知b2=25-a2,故所求双曲线方程可写为x2a2-y225-a2=1.∵点P-52,-6在所求双曲线上,∴代入有(-52)2a2-(-6)225-a2=1,化简得4a4-129a2+125=0,解得a2=1或a2=1254.当a2=1254时,b2=25-a2=25-1254=-254<0,不合题意,舍去,∴a2=1,b2=24,∴所求双曲线的标准方程为x2-y224=1.能力达标10.“mn<0”是方程“mx2+ny2=1表示双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案C解析因为mn<0,所以m,n均不为0且异号,方程mx2+ny2=1,可化为x21m+y21n=1,因为1m与1n异号,所以方程x21m+y21n=1表示双曲线,故“mn<0”是“方程mx2+ny2=1表示双曲线”的充分条件;反之,若mx2+ny2=1表示双曲线,则其方程可化为x21m+y21n=1,可知1m与1n异号,则必有mn<0,故“mn<0”是“方程mx2+ny2=1表示双曲线”的必要条件.综上可得,“mn<0”是方程“mx2+ny2=1表示双曲线”的充要条件.11.已知平面内两定点A(-5,0),B(5,0),动点M 满足|MA|-|MB|=6,则点M的轨迹方程是()A.x216-y29=1B.x216-y29=1(x≥4)C.x29-y216=1D.x29-y216=1(x≥3)答案D解析由|MA|-|MB|=6,且6A.双曲线的一支B.圆C.椭圆D.双曲线答案A解析设动圆的圆心为M,半径为r,圆x2+y2=1与x2+y2-8x+12=0的圆心分别为O1和O2,半径分别为1和2,由两圆外切的充要条件,得|MO1|=r+1,|MO2|=r+2.∴|MO2|-|MO1|=1,又|O1O2|=4,∴动点M的轨迹是双曲线的一支(靠近O1).13.若双曲线x2n-y2=1(n>1)的左、右焦点分别为F1,F2,点P在双曲线上,且满足|PF1|+|PF2|=2n+2,则△PF1F2的面积为()A.1B.12C.2D.4答案A解析设点P在双曲线的右支上,则|PF1|-|PF2|=2n,已知|PF1|+|PF2|=2n+2,解得|PF1|=n+2+n,|PF2|=n+2-n,|PF1|·|PF2|=2.又|F1F2|=2n+1,则|PF1|2+|PF2|2=|F1F2|2,∴△PF1F2为直角三角形,∠F1PF2=90°,∴S△PF1F2=12|PF1|·|PF2|=12×2=1.14.已知左、右焦点分别为F1,F2的双曲线C:x2a2-y2=1(a>0)过点15,-63,点P在双曲线C上,若|PF1|=3,则|PF2|=()A.3B.6C.9D.12答案C解析由左、右焦点分别为F1,F2的双曲线C:x2a2-y2=1(a>0)过点15,-63,可得15a2-69=1,解得a=3,b=1,c=10,a+c>3,点P在双曲线C 上,若|PF1|=3,可得P在双曲线的左支上,则|PF2|=2a+|PF1|=6+3=9.故选C.15.若曲线C:mx2+(2-m)y2=1是焦点在x轴上的双曲线,则m的取值范围为.答案(2,+∞)解析由曲线C:mx2+(2-m)y2=1是焦点在x轴上的双曲线,可得x21m-y21m-2=1,即有m>0,且m-2>0,解得m>2.16.焦点在x轴上的双曲线经过点(42,-3),且Q(0,5)与两焦点的连线互相垂直,则此双曲线的标准方程为.答案x216-y29=1解析设焦点F1(-c,0),F2(c,0)(c>0),则由QF1⊥QF2,得kQF1·kQF2=-1,∴5c·5-c=-1,∴c=5,设双曲线的标准方程为x2a2-y2b2=1(a>0,b>0),∵双曲线过点(42,-3),∴32a2-9b2=1.又c2=a2+b2=25,∴a2=16,b2=9,∴双曲线的标准方程为x216-y29=1.17.已知双曲线E:x216-y24=1的左、右焦点分别为F1,F2.(1)若点M在双曲线上,且MF1·MF2=0,求点M到x轴的距离;(2)若双曲线C与双曲线E有相同的焦点,且过点(32,2),求双曲线C 的方程.解(1)如图所示,不妨设点M在双曲线E的右支上,点M到x轴的距离为h,MF1·MF2=0,则MF1⊥MF2,设|MF1|=m,|MF2|=n,由双曲线定义,知m-n=2a=8,①又m2+n2=(2c)2=80,②由①②得mn=8,∴12mn=4=12|F1F2|·h,∴h=255.(2)设所求双曲线C的方程为x216-λ-y24+λ=1(-4(2)设以O为中心,F为其中一个焦点的双曲线经过点Q,如图所示,|OF|=c,m=64-1c2,当|OQ|取得最小值时,求此双曲线的标准方程.解(1)因为12|OF||FQ|sin(π-θ)=26,|OF||FQ|cosθ=m,所以tanθ=46m.又6θ<4,即tanθ的取值范围为(1,4).(2)设双曲线的标准方程为x2a2-y2b2=1(a>0,b>0),Q(x1,y1),则FQ=(x1-c,y1),所以S△OFQ=12|OF|·|y1|=26,则y1=±46c.又OF·FQ=m,即(c,0)·(x1-c,y1)=64-1c2,解得x1=64c,所以|OQ|=x12+y12=38c2+96c2≥12=23,当且仅当c=4时,取等号,此时|OQ|最小,这时Q的坐标为(6,6)或(6,-6).因为6a2-6b2=1,a2+b2=16,所以a2=4,b2=12.于是所求双曲线的标准方程为x24-y212=1.。

§ 2.3双曲线 2.3.1 双曲线及其标准方程课时目标 1.了解双曲线的定义、几何图形和标准方程的推导过程.2.掌握双曲线的标准方程.3.会利用双曲线的定义和标准方程解决简单的应用问题．1．双曲线的有关概念 (1)双曲线的定义平面内与两个定点F 1，F 2的距离的差的绝对值等于常数(小于________)的点的轨迹叫做双曲线．平面内与两个定点F 1，F 2的距离的差的绝对值等于|F 1F 2|时的点的轨迹为________________________________________________________________________． 平面内与两个定点F 1，F 2的距离的差的绝对值大于|F 1F 2|时的点的轨迹__________． (2)双曲线的焦点和焦距双曲线定义中的两个定点F 1、F 2叫做__________________，两焦点间的距离叫做__________________． 2．双曲线的标准方程(1)焦点在x 轴上的双曲线的标准方程是______________________，焦点F 1__________，F 2__________.(2)焦点在y 轴上的双曲线的标准方程是________________，焦点F 1__________，F 2__________.(3)双曲线中a 、b 、c 的关系是________________．一、选择题1．已知平面上定点F 1、F 2及动点M ，命题甲：||MF 1|－|MF 2||＝2a(a 为常数)，命题乙：M 点轨迹是以F 1、F 2为焦点的双曲线，则甲是乙的( ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．若ax 2＋by 2＝b(ab<0)，则这个曲线是( ) A ．双曲线，焦点在x 轴上 B ．双曲线，焦点在y 轴上 C ．椭圆，焦点在x 轴上 D ．椭圆，焦点在y 轴上3．焦点分别为(－2,0)，(2,0)且经过点(2,3)的双曲线的标准方程为( )A ．x 2－y 23＝1 B .x 23－y 2＝1C ．y 2－x 23＝1 D .x 22－y 22＝14．双曲线x 2m －y23＋m＝1的一个焦点为(2,0)，则m 的值为( )A .12 B ．1或3 C .1＋22 D .2－125．一动圆与两圆：x 2＋y 2＝1和x 2＋y 2－8x ＋12＝0都外切，则动圆圆心的轨迹为( )A ．抛物线B ．圆C ．双曲线的一支D ．椭圆6．已知双曲线中心在坐标原点且一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0,2)，则该双曲线的方程是( )A .x 24－y 2＝1B ．x 2－y 24＝1 C .x 22－y 23＝1 D .x 23－y22＝1二、填空题8．已知方程x 21＋k －y21－k＝1表示双曲线，则k 的取值范围是________．9．F 1、F 2是双曲线x 29－y216＝1的两个焦点，P 在双曲线上且满足|PF 1|²|PF 2|＝32，则∠F 1PF 2＝________________________________________________________________________. 三、解答题10．设双曲线与椭圆x 227＋y236＝1有相同的焦点，且与椭圆相交，一个交点A 的纵坐标为4，求此双曲线的标准方程．11．在△ABC 中，B(4,0)、C(－4,0)，动点A 满足sin B －sin C ＝12sin A ，求动点A 的轨迹方程．能力提升A ．[3－23，＋∞)B ．[3＋23，＋∞)C ．[－74，＋∞) D ．[74，＋∞)13．已知双曲线的一个焦点为F(7，0)，直线y ＝x －1与其相交于M ，N 两点，MN 中点的横坐标为－23，求双曲线的标准方程．1．双曲线的标准方程可以通过待定系数法求得． 2．和双曲线有关的轨迹问题要按照求轨迹方程的一般步骤来解，也要和双曲线的定义相结合．3．直线和双曲线的交点问题可以转化为解方程组(设而不求)，利用韦达定理，弦长公式等解决．§2.3 双曲线2.3.1 双曲线及其标准方程知识梳理1．(1)|F 1F 2| 以F 1，F 2为端点的两条射线 不存在 (2)双曲线的焦点 双曲线的焦距2．(1)x 2a 2－y 2b 2＝1(a >0，b >0) (－c,0) (c,0)(2)y 2a 2－x 2b 2＝1(a >0，b >0) (0，－c ) (0，c ) (3)c 2＝a 2＋b 2作业设计1．B [根据双曲线的定义，乙⇒甲，但甲 乙， 只有当2a <|F 1F 2|且a ≠0时，其轨迹才是双曲线．]2．B [原方程可化为x 2b a＋y 2＝1，因为ab <0，所以ba <0，所以曲线是焦点在y 轴上的双曲线，故选B.]3．A [∵双曲线的焦点在x 轴上，∴设双曲线方程为x 2a 2－y 2b 2＝1 (a >0，b >0)．由题知c ＝2，∴a 2＋b 2＝4.①又点(2,3)在双曲线上，∴22a 2－32b2＝1.②由①②解得a 2＝1，b 2＝3，∴所求双曲线的标准方程为x 2－y 23＝1.]4．A [∵双曲线的焦点为(2,0)，在x 轴上且c ＝2，∴m ＋3＋m ＝c 2＝4.∴m ＝12.]5．C [由题意两定圆的圆心坐标为O 1(0,0)，O 2(4,0)，设动圆圆心为O ，动圆半径为r ，则|OO 1|＝r ＋1，|OO 2|＝r ＋2，∴|OO 2|－|OO 1|＝1<|O 1O 2|＝4，故动圆圆心的轨迹为双曲线的一支．]6．B [设双曲线方程为x 2a 2－y 2b 2＝1，因为c ＝5，c 2＝a 2＋b 2，所以b 2＝5－a 2，所以x 2a 2－y 25－a 2＝1.由于线段PF 1的中点坐标为(0,2)，则P 点的坐标为(5，4)．代入双曲线方程得5a2－165－a 2＝1，解得a 2＝1或a 2＝25(舍去)，所以双曲线方程为x 2－y 24＝1.故选B.] 7．2解析 ∵||PF 1|－|PF 2||＝4，又PF 1⊥PF 2，|F 1F 2|＝25，∴|PF 1|2＋|PF 2|2＝20，∴(|PF 1|－|PF 2|)2＝20－2|PF 1||PF 2|＝16，∴|PF 1|²|PF 2|＝2. 8．－1<k <1解析 因为方程x 21＋k －y 21－k＝1表示双曲线，所以(1＋k )(1－k )>0.所以(k ＋1)(k －1)<0. 所以－1<k <1. 9．90°解析 设∠F 1PF 2＝α，|PF 1|＝r 1，|PF 2|＝r 2. 在△F 1PF 2中，由余弦定理，得(2c )2＝r 21＋r 22－2r 1r 2cos α，∴cos α＝ r 1－r 2 2＋2r 1r 2－4c 22r 1r 2＝36＋64－10064＝0.∴α＝90°.10．解 方法一 设双曲线的标准方程为y 2a 2－x 2b2＝1 (a >0，b >0)，由题意知c 2＝36－27＝9，c ＝3.又点A 的纵坐标为4，则横坐标为±15，于是有⎩⎪⎨⎪⎧42a2－ ±15 2b 2＝1，a 2＋b 2＝9，解得⎩⎪⎨⎪⎧a 2＝4，b 2＝5.所以双曲线的标准方程为y 24－x 25＝1. 方法二 将点A 的纵坐标代入椭圆方程得A (±15，4)， 又两焦点分别为F 1(0,3)，F 2(0，－3)． 所以2a ＝| ±15－0 2＋ 4＋3 2－ ±15－0 2＋ 4－3 2|＝4，即a ＝2，b 2＝c 2－a 2＝9－4＝5，所以双曲线的标准方程为y 24－x 25＝1.11．解 设A 点的坐标为(x ，y )，在△ABC 中，由正弦定理，得a sin A ＝b sin B ＝c sin C ＝2R ，代入sin B －sin C ＝12sin A ， 得|AC |2R －|AB |2R ＝12²|BC |2R ，又|BC |＝8，所以|AC |－|AB |＝4.因此A 点的轨迹是以B 、C 为焦点的双曲线的右支(除去右顶点)且2a ＝4,2c ＝8，所以a＝2，c ＝4，b 2＝12.所以A 点的轨迹方程为x 24－y 212＝1 (x >2)．12．B[由c ＝2得a 2＋1＝4，∴a 2＝3，∴双曲线方程为x 23－y 2＝1.设P (x ，y )(x ≥3)，13．解 设双曲线的标准方程为x 2a －y 2b＝1，且c ＝7，则a 2＋b 2＝7.①由MN 中点的横坐标为－23知，中点坐标为⎝ ⎛⎭⎪⎫－23，－53.设M (x 1，y 1)，N (x 2，y 2)，则由⎩⎪⎨⎪⎧x 21a －y 21b＝1，x 22a 2－y22b 2＝1，得b 2(x 1＋x 2)(x 1－x 2)－a 2(y 1＋y 2)(y 1－y 2)＝0. ∵⎩⎪⎨⎪⎧x 1＋x 2＝－43y 1＋y 2＝－103，且y 1－y 2x 1－x 2＝1， ∴2b 2＝5a 2.②由①，②求得a 2＝2，b 2＝5.∴所求双曲线的标准方程为x 22－y 25＝1.。

2．3.1 双曲线及其标准方程一、选择题1．若方程y 24－x 2m ＋1＝1表示双曲线，则实数m 的取值范围是( ) A ．－1<m <3B ．m >－1C ．m >3D ．m <－1[答案] B[解析] 依题意应有m ＋1>0，即m >－1.2．过点(1,1)，且b a ＝2的双曲线的标准方程是( ) A.x 212－y 2＝1 B.y 212－x 2＝1 C ．x 2－y 212＝1 D.x 212－y 2＝1或y 212－x 2＝1 [答案] D[解析] 由于b a ＝2，∴b 2＝2a 2.当焦点在x 轴上时，设双曲线方程为x 2a 2－y 22a 2＝1，代入(1,1)点，得a 2＝12.此时双曲线方程为x 212－y 2＝1.同理求得焦点在y 轴上时，双曲线方程为y 212－x 2＝1.3．若k >1，则关于x ，y 的方程(1－k )x 2＋y 2＝k 2－1所表示的曲线是( )A ．焦点在x 轴上的椭圆B ．焦点在y 轴上的椭圆C ．焦点在y 轴上的双曲线D ．焦点在x 轴上的双曲线[答案] C[解析] 将已知方程化为标准形式，根据项的系数符号进行判断．原方程可化为y 2k 2－1－x 21＋k ＝1.∵k >1，∴k 2－1>0,1＋k >0.∴已知方程表示的曲线为焦点在y 轴上的双曲线．4．双曲线8kx 2－ky 2＝8的一个焦点坐标为(0,3)，则k 的值是( )A ．1B ．－1 C.653 D ．－653[答案] B[解析] 原方程可化为x 21k －y 28k＝1，由焦点坐标是(0,3)可知c ＝3，且焦点在y 轴上，∴k <0.c 2＝－1k －8k ＝－9k＝9，∴k ＝－1，故选B. 5．若双曲线方程为x 2－2y 2＝1，则它的右焦点坐标为( )A ．(22，0) B ．(52，0) C ．(62，0) D ．(3，0)[答案] C[解析] 将方程化为标准方程x 2－y 212＝1， ∴c 2＝1＋12＝32，∴c ＝62，故选C. 6．设椭圆x 26＋y 22＝1和双曲线x 23－y 2＝1的公共焦点为F 1，F 2，P 是两曲线的一个公共点，则cos ∠F 1PF 2等于( ) A.14 B.13 C.19 D.35[答案] B[解析] 设|PF 1|＝d 1，|PF 2|＝d 2，则d 1＋d 2＝26，①|d 1－d 2|＝23，②①2＋②2，得d 21＋d 22＝18. ①2－②2，得2d 1d 2＝6.而c ＝2，∴cos ∠F 1PF 2＝d 21＋d 22－4c 22d 1d 2＝18－166＝13. 7．已知方程x 2m 2＋n －y 23m 2－n＝1表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是( )A.(－1，3)B.(－1，3)C.(0，3)D.(0，3)[答案] A[解析] ∵方程x 2m 2＋n －y 23m 2－n＝1表示双曲线，∴(m 2＋n )·(3m 2－n )>0，解得－m 2<n <3m 2，由双曲线性质，知c 2＝(m 2＋n )＋(3m 2－n )＝4m 2(其中c 是半焦距)，∴焦距2c ＝2×2|m |＝4，解得|m |＝1，∴－1<n <3，故选A.二、填空题8．已知双曲线x 225－y 29＝1的两个焦点分别为F 1，F 2，若双曲线上的点P 到点F 1的距离为12，则点P 到点F 2的距离为________．[答案] 22或2[解析] 设F 1为左焦点，F 2为右焦点，当点P 在双曲线左支上时，|PF 2|－|PF 1|＝10，|PF 2|＝22；当点P 在双曲线右支上时，|PF 1|－|PF 2|＝10，|PF 2|＝2.9．焦点在x 轴上的双曲线经过点P (42，－3)，且Q (0,5)与两焦点的连线互相垂直，则此双曲线的标准方程为______________．[答案] x 216－y 29＝1 [解析] 设焦点F 1(－c,0)，F 2(c,0)(c >0)，则由QF 1⊥QF 2，得kQF 1·kQF 2＝－1，∴5c ·5－c＝－1，∴c ＝5. 设双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)， ∵双曲线过(42，－3)，∴32a 2－9b 2＝1， 又∵c 2＝a 2＋b 2＝25，∴a 2＝16，b 2＝9.∴双曲线的标准方程为x 216－y 29＝1. 10．若双曲线x 216－y 2m＝1的焦距为10，则m ＝________. [答案] 9[解析] 由题意知，a ＝4，b ＝m ，c ＝5，又由a 2＋b 2＝c 2得，16＋m ＝25，∴m ＝9.11．已知双曲线x 2－y 2＝1，点F 1，F 2为其两个焦点，点P 为双曲线上一点，若PF 1⊥PF 2，则|PF 1|＋|PF 2|的值为________．[答案] 2 3[解析] 设P 在双曲线的右支上，|PF 1|＝2＋x ，|PF 2|＝x (x >0)，因为PF 1⊥PF 2， 所以(x ＋2)2＋x 2＝(2c )2＝8，所以x ＝3－1，x ＋2＝3＋1，所以|PF 2|＋|PF 1|＝3－1＋3＋1＝2 3.三、解答题12．已知△ABC 的一边的两个顶点B (－a,0)，C (a,0)(a >0)，另两边的斜率之积等于m (m ≠0)．求顶点A 的轨迹方程，并且根据m 的取值情况讨论轨迹的图形．解 设顶点A 的坐标为(x ，y )，则k AB ＝y x ＋a ，k AC ＝y x －a. 由题意，得y x ＋a ·y x －a＝m ，即x 2a 2－y 2ma 2＝1(y ≠0)． 当m >0时，轨迹是中心在原点，焦点在x 轴上的双曲线(除去x 轴的两个交点)；当m <0且m ≠－1时，轨迹是中心在原点，以坐标轴为对称轴的椭圆(除去与x 轴的两个交点)，其中当－1<m <0时，椭圆焦点在x 轴上；当m <－1时，椭圆焦点在y 轴上； 当m ＝－1时，轨迹是圆心在原点，半径为a 的圆(除去与x 轴的两个交点)．13．已知双曲线过点(3，－2)且与椭圆4x 2＋9y 2＝36有相同的焦点．(1)求双曲线的标准方程；(2)若点M 在双曲线上，F 1、F 2为左、右焦点，且|MF 1|＋|MF 2|＝63，试判断△MF 1F 2的形状．解 (1)椭圆方程可化为x 29＋y 24＝1，焦点在x 轴上，且c ＝9－4＝5，故设双曲线方程为x 2a 2－y 2b 2＝1， 则有⎩⎪⎨⎪⎧9a 2－4b 2＝1，a 2＋b 2＝5，解得a 2＝3，b 2＝2， 所以双曲线的标准方程为x 23－y 22＝1. (2)不妨设M 点在右支上，则有|MF 1|－|MF 2|＝23，又|MF 1|＋|MF 2|＝63，故解得|MF 1|＝43，|MF 2|＝23，又|F 1F 2|＝25，因此在△MF 1F 2中，|MF 1|边最长，而cos ∠MF 2F 1＝|MF 2|2＋|F 1F 2|2－|MF 1|22·|MF 2|·|F 1F 2|<0， 所以∠MF 2F 1为钝角．故△MF 1F 2为钝角三角形.。

课时作业10 双曲线及其标准方程 |基础巩固|(25分钟，60分)一、选择题(每小题5分，共25分)1．已知F 1(－8,3)，F 2(2,3)，动点P 满足|PF 1|－|PF 2|＝10，则P 点的轨迹是( )A ．双曲线B ．双曲线的一支C ．直线D ．一条射线解析：F 1，F 2是定点，且|F 1F 2|＝10，所以满足条件|PF 1|－|PF 2|＝10的点P 的轨迹应为一条射线．答案：D 2．已知双曲线方程为x 2－2y 2＝1，则它的右焦点坐标为( ) A.⎝ ⎛⎭⎪⎫22，0 B.⎝ ⎛⎭⎪⎫52，0 C.⎝ ⎛⎭⎪⎫62，0 D ．(3，0) 解析：将双曲线方程化为标准方程，即x 21－y 212＝1，∴a 2＝1，b 2＝12，∴c ＝a 2＋b 2＝62，∴右焦点坐标为⎝ ⎛⎭⎪⎫62，0.答案：C3．焦点分别为(－2,0)，(2,0)且经过点(2,3)的双曲线的标准方程为( )A ．x 2－y 23＝1 B.x23－y 2＝1C ．y 2－x 23＝1 D.x 22－y 22＝1 解析：由双曲线定义知，2a ＝(2＋2)2＋32－(2－2)2＋32＝5－3＝2， ∴a ＝1.又c ＝2，∴b 2＝c 2－a 2＝4－1＝3，因此所求双曲线的标准方程为x 2－y23＝1.答案：A4．下面各选项中的双曲线，与x212－y224＝1共焦点的双曲线是()A.x212＋y214＝1 B.y224－x212＝1C.x210－y226＝1 D.x210＋y226＝1解析：方法一因为所求曲线为双曲线，所以可排除选项A，D；又双曲线x212－y224＝1的焦点在x轴上，所以排除选项B，综上可知，选C.方法二与x212－y224＝1共焦点的双曲线系方程为x212＋λ－y224－λ＝1，对比四个选项中的曲线方程，发现只有选项C中的方程符合条件(此时λ＝－2)．答案：C5．已知定点A，B且|AB|＝4，动点P满足|P A|－|PB|＝3，则|P A|的最小值为()A.12 B.32C.72D．5解析：如图所示，点P是以A，B为焦点的双曲线的右支上的点，当P在M处时，|P A|最小，最小值为a＋c＝32＋2＝72.答案：C二、填空题(每小题5分，共15分)6．设m是常数，若点F(0,5)是双曲线y2m－x29＝1的一个焦点，则m＝________.解析：由点F(0,5)可知该双曲线y2m－x29＝1的焦点落在y轴上，所以m>0，且m＋9＝52，解得m＝16.答案：167．已知P是双曲线x264－y236＝1上一点，F1，F2是双曲线的左、右焦点，且|PF1|＝17，求|PF2|＝________.解析：由双曲线方程x264－y236＝1可得a＝8，b＝6，c＝10，由双曲线的图象可得点P到右焦点F2的距离d≥c－a＝2.因为||PF1|－|PF2||＝16，|PF1|＝17，所以|PF2|＝1(舍去)或|PF2|＝33.答案：338．已知双曲线E：x2a2－y2b2＝1(a>0，b>0)．若矩形ABCD的四个顶点在E上，AB，CD的中点为E的两个焦点，且2|AB|＝3|BC|，则E的标准方程是________．解析：如图，由题意不妨设|AB|＝3，则|BC|＝2.设AB，CD的中点分别为M，N，在Rt△BMN中，|MN|＝2c＝2，故|BN|＝|BM|2＋|MN|2＝⎝⎛⎭⎪⎫322＋22＝52.由双曲线的定义可得2a＝|BN|－|BM|＝52－32＝1，即a2＝14.而2c＝|MN|＝2，从而c＝1，b2＝34. 所以双曲线E的标准方程是x214－y234＝1.答案：x214－y234＝1三、解答题(每小题10分，共20分)9．已知x21－k－y2|k|－3＝－1，当k为何值时，(1)方程表示双曲线？|能力提升|(20分钟，40分)11．已知点M (－3,0)，N (3,0)，B (1,0)，动圆C 与直线MN 切于点B ，过M ，N 与圆C 相切的两直线相交于点P ，则点P 的轨迹方程是( )A ．x 2－y 28＝1(x >1)B ．x 2－y28＝1(x <－1)C ．x 2＋y 28＝1(x >0)D ．x 2－y 210＝1(x >1)解析：如图，设过M ，N 的直线与圆C 相切于R ，S ，则|PR |＝|PS |，|MR |＝|MB |，|SN |＝|NB |， 所以|PM |＝|PR |＋|RM | ＝|PR |＋|MB |， |PN |＝|PS |＋|SN | ＝|PS |＋|NB |，所以|PM |－|PN |＝|MB |－|NB | ＝2<|MN |，所以由双曲线定义知，P 点的轨迹是以M (－3,0)，N (3,0)为焦点的双曲线的右支，因为2a ＝2，所以a ＝1，c ＝3， 所以b 2＝c 2－a 2＝8，所以点P 的轨迹方程为x 2－y28＝1(x >1)． 故选A. 答案：A12．已知双曲线的两个焦点F 1(－5，0)，F 2(5，0)，P 是双曲线上一点，且PF 1→·PF 2→＝0，|PF 1|·|PF 2|＝2，则双曲线的标准方程为______________．解析：由题意可设双曲线方程为由Ruize收集整理。