深受弯构件

第11章深受弯构件钢筋混凝土深受弯构件是指跨度与其截面高度之比较小的梁。

按照《公路桥规》的规定，梁的计算跨径l与梁的高度h之比l/h≤5的受弯构件称为深受弯构件。

深受弯构件又可分为短梁和深梁：l/h≤2的简支梁和l/h≤2.5的连续梁定义为深梁；2＜l/h≤5的简支梁和2.5＜l/h≤5的连续梁称为短梁。

钢筋混凝土深受弯构件因其跨高比较小，且在受弯作用下梁正截面上的应变分布和开裂后的平均应变分布不符合平截面假定，故钢筋混凝土深受弯构件的破坏形态、计算方法与普通梁（定义为跨高比l/h＞5的受弯构件）有较大差异。

11.1深受弯构件的破坏形态11.1.1 深梁的破坏形态简支梁主要有以下三种破坏形态。

1）弯曲破坏当纵向钢筋配筋率ρ较低时，随着荷载的增加，一般在最大弯矩作用截面附近首先出现垂直于梁底的弯曲裂缝并发展成为临界裂缝，纵向钢筋首先达到屈服强度，最后，梁顶混凝土被压碎，深梁即丧失承载力，被称为正截面弯曲破坏[图11-1a)]。

当纵向钢筋配筋率ρ稍高时，在梁跨中出现垂直裂缝后，随着荷载的增加，梁跨中垂直裂缝的发展缓慢，在弯剪区段内由于斜向主拉应力超过混凝土的抗拉强度出现斜裂缝。

梁腹斜裂缝两侧混凝土的主压应力，由于主拉应力的卸荷作用而显著增大，梁内产生明显的应力重分布，形成以纵向受拉钢筋为拉杆，斜裂缝上部混凝土为拱腹的拉杆拱受力体系[图11-1c)]。

在此拱式受力体系中，受拉钢筋首先达到屈服而使梁破坏，这种破坏被称为斜截面弯曲破坏[图11-1b)]。

χ)β)α)图11-1 简支深梁的弯曲破坏a)正截面弯曲破坏b)斜截面弯曲破坏c)拉杆拱受力图式2）剪切破坏当纵向钢筋配筋率较高时，拱式受力体系形成后，随着荷载的增加，拱腹和拱顶（梁顶受压区）的混凝土压应力亦随之增加，在梁腹出现许多大致平行于支座中心至加载点连线的斜裂缝。

最后梁腹混凝土首先被压碎，这种破坏称为斜压破坏[图11-2a)]。

深梁产生斜裂缝之后，随着荷载的增加，主要的一条斜裂缝会继续斜向延伸。

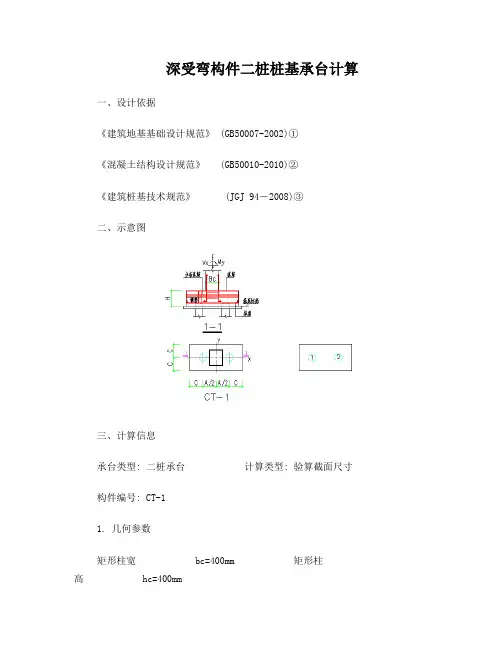
深受弯构件二桩桩基承台计算一、设计依据《建筑地基基础设计规范》 (GB50007-2002)①《混凝土结构设计规范》 (GB50010-2010)②《建筑桩基技术规范》 (JGJ 94－2008)③二、示意图三、计算信息承台类型: 二桩承台计算类型: 验算截面尺寸构件编号: CT-11. 几何参数矩形柱宽 bc=400mm 矩形柱高 hc=400mm圆桩直径 d=400mm承台根部高度 H=700mmx方向桩中心距 A=1400mm承台边缘至边桩中心距 C=400mm2. 材料信息柱混凝土强度等级: C30 ft_c=1.43N/mm2, fc_c=14.3N/mm2承台混凝土强度等级: C30 ft_b=1.43N/mm2, fc_b=14.3N/mm2桩混凝土强度等级: C80 ft_p=2.22N/mm2, fc_p=35.9N/mm2 承台钢筋级别: HRB400 fy=360N/mm2承台箍筋级别: HRB400 fyv=360N/mm2水平分布筋钢筋级别: HRB400 fyh=360N/mm23. 计算信息结构重要性系数: γo=1.0纵筋合力点至近边距离: as=70mm4. 作用在承台顶部荷载基本组合值F=1000.000kNMx=0.000kN*mMy=0.000kN*mVx=0.000kNVy=0.000kN5. 配筋信息水平分布筋直径：12mm，间距：sv=100mm箍筋直径：12mm，间距：sh=100mm受拉筋最小配筋率：ρmin= 0.20%箍筋最小配筋率：ρsvmin= 0.20%水平分布筋最小配筋率：ρshmin= 0.20%箍筋面积：Asv=226mm2水平分布筋面积：Ash=226mm2四、计算参数1. 承台总长 Bx=C+A+C=0.400+1.400+0.400=2.200m2. 承台总宽 By=C+C=0.400+0.400=0.800m3. 承台根部截面有效高度 ho=H-as=0.700-0.070=0.630m4. 圆桩换算截面宽度 bp=0.8*d=0.8*0.400=0.320m五、内力计算1. 各桩编号及定位座标如上图所示:1号桩 (x1=-A/2=-0.700m, y1=0m)2号桩 (x2= A/2=0.700m, y2=0m)2. 各桩净反力设计值, 计算公式:Ni=F/n+My*xi/∑xi2+Vx*H*xi/∑xi2【8.5.3-2】①N1=1000.000/2+0.000*(-0.700)/((-0.700)2*2)+0.000*0.700*(-0.700)/((-0.700)2*2)=500.000kNN2=1000.000/2+0.000*0.700/(0.7002*2)+0.000*0.700*0.700/(0.7002*2)=500.000kN六、承台斜截面受剪计算1. 得到承台底面处的最大剪力值V=γo*max(|N1|, |N2|)=500.000kN2. 计算梁截面有效高度和腹板高度ho=H-as=700-70=630mmhw=ho=630mm3. 确定跨高比lo =min(1.15*(A-ls),A)=1400mmlo/H=1400/700=2.000V=γo*max(|N1|, |N2|)=500.000kNb=2C=800mm当hw/b=630/800=0.787≤4 时V≤(1/60)*(10+lo/H)*(βc*fc*b*ho)/γo混规(G.0.3-1)②=(1/60)*(10+2.000)*(1.0*14.3*800*630)/1.0=1441.440kN 截面符合条件。

对深受弯构件受力特点的探讨针对深受弯构件与普通钢筋混凝土梁的不同特点，简要对比了新旧混凝土结构设计规范中深受弯构件的承载力计算公式、构造等思路及要求，突出了新规范的改进创新之处。

标签深受弯构件；规范；承载力；构造1 深受弯构件的受力特点钢筋混凝土深受弯构件是指跨高比较小（l0 /h<5）的受弯构件。

深受弯构件因其跨度与高度相近，在荷载作用下同时兼有受压、受弯和受剪状态，受力特性与普通梁有一定的差别，其正截面应变不符合平截面假定，自顶面到底面呈明显的曲线变化，在跨高比很小时，甚至出现了多个应变为零的点。

但随着跨高比的变化，受力特性会有显著的变化，对于简支梁，在跨高比l0 /h ≤2时，截面应变曲线特征明显，规范将其列为深梁；在跨高比2<l0 /h≤5时，截面应变逐渐由曲线回归到平截面假定的状况，规范将其列为短梁。

文中应用通用有限元程序Ansys，对不同跨高比的简支梁在均部荷载下跨中截面的截面正应力进行了计算，并绘出自顶面到底面的变化情况。

2 新规范的计算公式2.1 正截面受弯破坏形态及承载力计算短梁的破坏形态和普通梁相同。

根据配筋的量有适筋破坏、超筋破坏和少筋破坏。

对于深梁，当跨中的纵向受拉钢筋首先达到屈服强度时，深梁即发生正截面弯曲破坏。

其特点是：破坏开始时深梁的挠度较小，但在弯坏的过程中却有较大的延性，当纵向受拉钢筋的配筋率增加到某一程度时，深梁的破坏形态将由弯曲破坏转化为剪切破坏，此时的配筋率称为弯剪界限配筋率；当纵筋配筋量继续增大时，将出现弯剪区斜裂缝开展较跨中垂直裂缝快的现象，并形成所谓拉力拱的受力体系，因此，深梁不会出现超筋破坏形态。

无水平分布筋的深受弯构件，规范中正截面受弯承载力设计值Mu 可按下列公式计算：Mu=?yAsz （1）其中，fy，As 分别为纵向钢筋的抗拉强度设计值和截面面积；z为内力臂。

该公式力学含义非常明确，并且力学含义与深受弯构件的受力特性相吻合，新规范与旧规范在Mu的计算公式上是一致的，只是公式中内力臂z的计算有所不同，新规范内力臂考虑了跨高比（l0 /h）的影响，下面比较了新旧规范内力臂z的计算：旧规范：z=0.1（l0 +5.5h）（当l0 <h时，z =0.65h0）（2）新规范：z= αd（h0—x/2）（3）αd=0.8+0.04（l0 /h）（当l0<h时，z=0.6h0）（4）内力臂z来源于试验成果，使构件正截面计算变得简单，新规范公式较旧规范公式提高了构件安全度，考虑了跨高比（l0 /h的连续变化对构件受力性能的影响，并且实现了与普通梁正截面承载力公式的衔接问题（l0 /h=5时，αd=1.0，从而z=ho— x/2，即为普通梁的内力臂取值）。

梁截面：b=800mm h=1000mm1400mmfy=360fc=14.3α1=1β1=0.8Es=2fcu.k=20.1N/mm*mmγo=1as=0.1*h=100mmM=525KN*M αcv=0.7n=4Asv1=79mm 2fyv=360N/mm*mm （砼4.2.3）Asv=n*Asv=316mm2s=100mm ft=1.43N/mm*mm二、计算：βc=10.8569792.64mm²X1=1738.318mmX2=61.68227mm εcu=0.00330.75862069682.7586mm180mm 693.36mm 2103.284489mm 20.262910561743.9999883mm1960.125479mm 20.245015685840mm 1736.111111mm 20.217013889V=2700KN1956240N=1956.24KN钢筋混凝土深受弯构件一、基本资料：N/mm*mm （砼6.2.6）M≤fy*As*Z 梁计算跨度： lo=类型（一）：当ho/b不大于4时，1、正截面受弯承载力计算：内力臂Z=ad*(ho-0.5*X)=类型（一）：当lo≥h时，（砼4.2.5）N/mm*mm（砼6.2.6）（砼4.1.（砼6.3.1）②当X≥0.2ho时ξb=β1/(1+fy/Es/εcu)=①当X<0.2ho时，X=0.2ho=内力臂计算：αd=0.8+0.04*lo/h=令：A=α1*fc*b*ad=则：X=（A*ho±√（A²*ho²-2*A*M））/A X≤ξb*ho=内力臂Z=ad*(ho-0.5*X)=％≥ρmin=0.200％ 满足要求属适筋情况，受压区满足要求。

As=M/(fy*z)*γo=配筋率：ρ=As/(b*h)=类型（一）：当ho/b不小于6时，2、受剪承载力计算：As=M/(fy*z)*γo=％≥ρmin=0.200％ 满足要求类型（二）：当lo<h时，内力臂Z=0.6*lo=配筋率：ρ=As/(b*h)=As=M/(fy*z)*γo=配筋率：ρ=As/(b*h)=V≤（10+lo/h）*βc*fc*b*ho/60=Z=ad*(ho-0.5*X)α1*fc*b*X=fy*As(砼6.2.10-2)M=fy*As*Z=fy*As*ad*(ho-0.5*X)=α1*fc*b*X*ad*(ho-0.5*X)％≥ρmin=0.200％ 满足要求1441440N=1441.44KN1023.84KN720.72KNV=Vc+Vs=1744.56KN3、箍筋计算（估算）：箍筋所抵抗的剪力为：Vs=fyv*Asv*h0/s=混凝土所抵抗的剪力为：V c=0.7*ft*b*h0=V≤（7+lo/h）*βc*fc*b*ho/60=需注意需修改计算结果分类1分类2需要结果2980KN*M 525KN*MV=ql=6750KN V=P=1500KN2、梁上为集中荷载时砼4.1.3）2<lo/h<5, 属于一般深受弯构件。

附录G 深受弯构件G.0.1简支钢筋混凝土单跨深梁可采用由一般方法计算的内力进行截面设计；钢筋混凝土多跨连续深梁应采用由二维弹性分析求得的内力进行截面设计。

G.0.2钢筋混凝土深受弯构件的正截面受弯承载力应符合下列规定：M≤fAz（G.0.2-1）sy z＝α（h－0.5x）（G.0.2-2）0dα＝0.80＋0.04l/h（G.0.3-3）0d 当l＜h 时，取内力臂z＝0.6l。

00式中：x——截面受压区高度，按本规范公式第 6.2 节计算；当x＜0.2h时，取x＝00.2h；0——截面有效高度：h/h≤2 时，跨中截面al，其中h h为截面高度；当h-a＝s 000s取0.1h，支座截面a取0.2h；当l/h＞2 时，a按受拉区纵向钢筋截面重心至受拉边s s 0缘的实际距离取用。

G.0.3钢筋混凝土深受弯构件的受剪截面应符合下列条件：当h/b 不大于 4 时w（G.0.3-1）当h/b 不小于 6 时w）G.0.3-2（当h/b 大于 4 且小于 6 时，按线性内插法取用。

w式中：V——剪力设计值；——计算跨度，当l 小于h 时，取2h；l 00b——矩形截面的宽度以及Ｔ形、Ｉ形截面的腹板厚度；——截面高度、截面有效高度；h、h0——截面的腹板高度：对矩形截面，取有效高度h；对Ｔ形截面，取有效高度h0w减去翼缘高度；对Ｉ形和箱型截面，取腹板净高；——混凝土强度影响系数，按本规范第 6.5 节的规定取用。

βc G.0.4矩形、T形和I形截面的深受弯构件，在均布荷载作用下，当配有竖向分布钢筋和水平分布钢筋时，其斜截面的受剪承载力应符合下列规定：（G.0.4-1）对集中荷载作用下的深受弯构件（包括作用有多种荷载，且其中集中荷载对支座截面所产生的剪力值占总剪力值的75％以上的情况），其斜截面的受剪承载力应符合下列规定：（G.0.4-2）式中：λ——计算剪跨比：当l/h 不大于 2.0 时，取λ＝0.25；当l/h 大于 2 且小于 5 00时，取λ＝a/h，其中，a 为集中荷载到深受弯构件支座的水平距离；λ的上限值为0（0.92l/h－1.58），下限值为（0.42l/h－0.58）；00l/h——跨高比，当l/h 小于 2 时，取 2.0。

对深受弯构件受力特点的探讨弯构件作为一类常见的结构构件，其受力特点因其特有的几何形状和材料性能等因素而具有一定的复杂性和多样性。

同时，深受弯构件，即弯曲半径与截面尺寸之比较小的构件，在受力方面更加突出其独特性。

因此，探讨深受弯构件受力特点，对于科学地分析和设计这类结构具有重要意义。

一、深受弯构件的受力特点1.1 柔度较大深受弯构件受力时，受力点处产生的应力较大，导致构件产生较大的弯曲变形，因此柔度较大，即弯曲挠度较大。

同时，由于受力点的应力集中作用，一些部位容易发生裂纹，或者出现舒适变形，增加了构件的变形和破坏风险。

1.2 剪力作用较大由于深受弯构件的截面弯曲半径较小，因此在其受力状态下，其截面形态发生了变化，出现了截面形心偏移现象。

这导致构件内部产生了较大的剪力作用。

同时，在构件两端也会产生弯矩反转的现象，也加剧了构件内部的剪力作用。

1.3 侧向约束要求较高由于深受弯构件的截面一般为异形，因此不仅需要考虑弯曲变形和剪力作用，还需要考虑截面约束条件下的侧向位移和变形。

这要求在设计和施工过程中，需要对其侧向约束进行充分考虑和处理，避免出现截面失稳现象，影响构件的安全性。

二、深受弯构件的承载能力从理论上讲，深受弯构件在截面弯曲半径一定时，可以经受与非受弯构件相同的弯曲力和拉伸力。

然而，在实际应用中，由于深受弯构件的剪力作用较大，其承载能力会受到一定程度的影响。

具体来说，对于深受弯构件，其可承载的弯曲力主要取决于其抗剪力大小。

因此，在设计和施工深受弯构件时，需要重视其剪力作用的影响，避免其产生非正常受力状态或破坏。

三、深受弯构件的应用领域由于深受弯构件的柔度较大，一些应用领域的要求不高，主要应用于一些低层民用建筑、简单桥梁、临时构筑物、装饰工程等方面。

同时，在一些轻型钢结构方面，深受弯构件也有着广泛的应用。

四、深受弯构件的优化设计针对深受弯构件的受力特点和应用领域，有必要提出一些优化设计的建议：4.1 加强结构侧向约束条件，采用更优化的截面形状，避免出现截面失稳现象，降低构件的挠度和变形风险。

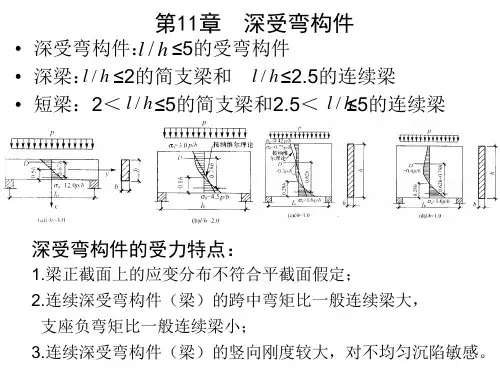
深受弯构件水平分布钢筋面积计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: L-1二、设计依据《混凝土结构设计规范》 GB50010-2010三、计算信息1. 几何参数梁宽: b=600mm梁高: h=2000mm梁的计算跨度: lo=3600mm2. 材料信息混凝土等级: C30 fc=14.3N/mm2ft=1.43N/mm2水平分布钢筋种类: HRB335 fyh=300N/mm2水平分布钢筋间距: Sv=100mm竖向分布钢筋种类: HRB335 fyv=300N/mm2竖向分布钢筋间距: Sh=150mm水平分布钢筋最小配筋率: ρsh,min=0.200％(自动计算)竖向分布钢筋最小配筋率: ρsv,min=0.200％(自动计算)纵筋合力点至近边距离: as=0.1h=0.1*2000=200mm3. 荷载信息V=500.000kN4. 配筋信息Asv=500mm25. 设计参数结构重要性系数: γo=1.1四、计算过程1. 判断深受弯构件类型lo/h=3600/2000=1.800≤2.5, 属于深梁。

2. 计算梁截面有效高度和腹板高度ho=h-as=2000-200=1800mmhw=ho=1800mm3. 确定跨高比lo/h=3600/2000=1.800<2.0, 取lo/h=2.000。

4. 确定受剪面是否符合条件当hw/b=1800/600=3.000≤4 时V≤(1/60)*(10+lo/h)*(βc*fc*b*ho)/γo 混规(G.0.3-1)=(1/60)*(10+2.000)*(1.0*14.3*600*1800)/1.1=2808.000kN 截面符合条件。

5. 确定是否需按构造配筋[0.7*(8-lo/h)*ft*b*ho/(3*1000)+1.25*(lo/h-2)*fyv*Asv*ho/(3*Sh*1000)]/γo=[0.7*(8-2.000)*1.43*600*1800/(3*1000)+1.25*(2.000-2)*300*500*1800/(3*150*1000)]/1.1 =1965.600≥V=500.000kN不需进行配筋计算，仅需按构造要求配箍。

深受弯构件纵向受拉钢筋面积计算
深受弯构件纵向受拉钢筋面积是指在梁或柱的纵向受拉区域内所需要的钢筋截面积。

深受弯构件是指受到较大弯曲力作用的结构构件，通常用于承受较大荷载或梁柱的支承距离较大的情况下。

计算深受弯构件的纵向受拉钢筋面积需要考虑到结构的荷载情况、钢筋的抗拉强度和构件的几何尺寸等因素。

计算深受弯构件纵向受拉钢筋面积的一般步骤如下：
1.首先，确定深受弯构件的几何尺寸和力学特性。

包括结构的几何尺寸（如截面尺寸、悬臂长度等）、截面形状（常见的有矩形截面、T形截面等）、截面受力性能（如抗弯强度、抗剪强度等）等。

2.根据深受弯构件的受力情况，确定钢筋的布置方式。

钢筋可以采用单筋布置、双筋布置或多筋布置等形式，具体取决于构件的受力和设计要求。

3.根据深受弯构件的荷载情况和边界条件，计算纵向受拉力大小。

纵向受拉力的大小取决于施加到构件上的荷载大小和受力区域的长度。

4.根据结构的设计要求和性能要求，确定钢筋的抗拉强度。

钢筋的抗拉强度通常使用屈服强度或抗拉强度来表示，这取决于钢筋的材质和规定要求。

5. 根据纵向受拉力和钢筋抗拉强度，计算所需要的钢筋面积。

钢筋面积的计算公式通常为：As = F / (fy × γs)，其中As为钢筋面积，F 为纵向受拉力，fy为钢筋的抗拉强度，γs为钢筋的安全系数。

以上是计算深受弯构件纵向受拉钢筋面积的一般步骤。

在实际设计中，还需要根据具体的设计要求和规范要求进行修正和调整。

同时，还需要注
意结构的整体性能和稳定性的考虑，以满足结构的安全和使用要求。

桥梁深受弯构件探讨摘要：探讨桥梁深受弯构件与一般梁在内力计算中的差异，并指出深受弯构件在内力计算时要注意的问题，同时总结了深受弯构件强度验算相对两个规范之间的差异，应用于桥梁中深受弯构件的设计。

关键词：深受弯构件，短梁，深梁，弯矩，剪力，配筋在大跨连续梁桥以及斜拉桥设计中，在中墩横梁、桥塔下横梁位置，横梁截面高度比较高，如果支座间距比较小，就会有其长细比（亦称跨高比）—计算跨度与截面高度之比比较小的情况，当简支梁，连续梁时，称为“短梁”；当简支梁，连续梁时，称为“深梁”（原桥梁规范）。

水工部门和建筑部门将“短梁”和“深梁”统称为深受弯构件。

本文将重点讨论桥梁设计中深受弯构件的计算过程及相应计算结果的比较。

短梁、深梁、常规梁的内力计算比较简支深受弯构件与常规梁的内力计算方法一致，本条将讨论短梁、深梁、常规梁为连续梁情况下的内力计算。

通过试验分析确定的具有不同跨高比的均质弹性简支梁( 开裂前)在承受均布荷载W时, 其跨中水平弯曲盈利的分布情况可以看出: 深梁的正截面应变分布不再符合平截面假定, 而且跨高比越小, 这种现象就越明显。

这是由于深梁的尺寸比例与普通钢筋混凝土浅梁不同,故其性能与其说属于一维构件, 不如说是二维构件, 且为双向受力。

因此, 受弯前为平面的截面, 受弯后不再保持平面, 应力分布也不能再看作是线性的。

而在普通梁中被略去不及的剪切变形, 现在深梁中要比纯弯矩所产生的变形大的多。

因此受压区的应力分布, 即使还在弹性阶段, 已经属于非线性性质; 在极限荷载阶段, 混凝土中的压应力分布不像普通梁那样成抛物形曲线分布, 应力值也不相同。

此外, 这种梁开裂厚将引起内力重新分布, 从而使梁的破坏特征和承载力也与普通钢筋混凝土梁不同, 随着跨高比的减小, 这些差异会更加明显。

为了验证这一结论，采用有限单元计算方法，通过实体单元与梁单元两种模型，计算梁截面内力的差异。

（验证所采用的软件为MIDAS）（1）、长细比时的内力情况（短梁）图一短梁构件立面、断面示意图由上图知：加载方式按总重240000kN，其中实体单元按上表面的面荷载加载q=2500 kN/m2；梁单元按均布荷载q=10000kN/m计。

深受弯构件定义
深受弯构件定义是一种机械工程领域的术语，指的是某些金属材料在设计、制造和安装过程中遵循的一系列准则。

它定义了构件的形状、结构、弯曲度等关键因素，并为构件的安全使用提供了一致而可靠的标准。

深受弯构件定义主要包括以下几个方面：
1. 构件形状：深受弯构件定义将构件分为开口弯曲和闭口弯曲两种不同的形式。

开口弯曲形式的构件具有一定程度的弹性，但它们不能提供太多的支撑力，因此不能用于支撑重物。

而闭口弯曲构件则具有很好的支撑力，可以用于支撑重物。

2. 构件结构：深受弯构件定义还将构件分为折弯和翻边两种不同的结构。

折弯构件具有比较小的半径，但是具有较大的弯曲度，因此可以支撑重物；而翻边构件具有较大的半径，但是具有较小的弯曲度，因此不能支撑重物。

3. 构件弯曲度：构件的弯曲度是指构件在长度方向上的弯曲程度。

深受弯构件定义包括对构件弯曲度的准确测量，可以根据构件的实际情况来确定构件的最佳弯曲度，以保证构件的安全性和可靠性。

4. 构件安装：深受弯构件定义还涉及到构件的安装，具体包括构件的安装位置、安装方式、安装固定以及安装
时间等。

在安装过程中，应确保构件按照正确的安装方法进行安装，以保证构件的安全性和可靠性。

深受弯构件定义的主要目的是确保金属构件在使用过程中具有良好的安全性和可靠性。

通过深受弯构件定义，可以确保构件在设计、制造和安装过程中都遵循同一系列标准，从而有效地预防金属构件在使用过程中可能出现的问题。

概念：深梁deep beam一般指梁的跨度与高度之比L／h≤2的简支梁和L／h≤2．5的连续梁，且适用于本身直接承受竖向荷载为主的深梁（剪力墙结构的连系梁虽然尺寸接近深梁，但其支座条件不同，梁的剪切变形较大，故不在本条之列）。

深梁因其高度与跨度接近，受力性能与一般梁有较大差异，在荷载作用下，梁的正截面应变不符合平截面假定。

为避免深梁出平面失稳，规范对梁截面高宽比（h／b）或跨宽比（L0／h）作了限制（截面宽度不小于140mm，当Lo/h≥1时，h/b不宜大于25，当Lo/h<1时，Lo/b不宜大于25），并要求简支深梁在顶部、连续深梁在顶部和底部尽可能与其它水平刚度较大的构件（如楼盖）相连接。

简支深梁的内力计算与浅梁相同。

但连续深梁的弯矩及剪力与一般连续梁不同，其跨中正弯矩比一般连续梁偏大，支座负弯矩则偏小，且随跨高比及跨数的不同而变化。

工程设计中，对连续深梁内力按弹性力学方法计算，暂不考虑塑性内力重分布。

试验表明，简支深梁在斜裂缝出现后，梁内即发生明显的内力重分布，形成以纵向受拉钢筋为拉杆、斜裂缝上部混凝土为拱肋的拉杆拱受力体系。

深梁的受剪承载力主要取决于截面尺寸、混凝土强度等级和剪跨比，其次为支承长度，分布钢筋，尤其竖向分布筋作用较小。

深梁支座的支承面和集中荷载的加荷点都是高应力区，易发生局压破坏，应进行局压承载力计算。

深梁是较复杂的构件，应遵守规范有关要求。

1、深受弯构件分类钢筋混凝土受弯构件根据其跨度与高度之比（简称跨高比）的不同，可以分为如下三种类型：浅深：短梁：深梁：(简支梁)（连续梁）式中，h为梁截面高度；L0为梁的计算跨度，可取Lc和1.15Ln两者中较小值，Lc为支座中心线之间的距离，Ln为梁的净跨。

浅梁在实际工程中量大面广，可称为一般受弯构件。

短梁和深梁又称为深受弯构件。

深受弯构件在建筑工程中的应用已日渐广泛。

2、承载力计算钢筋混凝土深受弯构件的正截面受弯承载力应按下列公式计算：（4-54）（4-55）（4-56）当时，取内力臂。

深受弯构件5.2.2深受弯构件斜截面设计◆深受弯构件斜截面受剪承载力计算▲计算公式矩形、T形和I形截面的深受弯构件，在均布荷载作用下，当配有竖向分布钢筋和水平分布钢筋时，其斜截面的受剪承载力应按下列公式计算：(5-18)对集中荷载作用下的深受弯构件（包括作用有多种荷载，且其中集中荷载对支座截面或节点边缘截面所产生的剪力值点总剪力值的75%以上的情况），其斜截面的受剪承载力应按下列公式计算：(5-19)当l0/h＜2.0时，取l0/h=2.0。

当ρsh=A sh/bs v＞0.75%时，取ρsh=0.75%。

式中λ——计算剪跨比，当l0/h不大于2.0时，取λ=0.25；当2.0＜l0/h＜5.0时，取λ=a/h0，其中，a为集中荷载到深受弯构件支座的水平距离，λ的上限值按λu=0.917l0/h-1.584计算；λ的下限值按λu=0.417l0/h-0.584计算；l0/h——跨高比。

如果将l0/h=5分别代入公式（5-18）和（5-19）中，不难看到，它们将与公式（5-7）和（5-8）完全相同，说明深受弯构件斜截面受剪承载力计算公式与一般受弯构件受剪承载力计算公式是相互衔接的。

▲截面尺寸要求当h w/b≤4时：(5-20) 当h w/b≥6时：(5-21)当4＜h w/b＜6时，按线性内插法取用。

当l0/h＜2时，取l0/h=2.0。

式中V——剪力设计值；l0——计算跨度；b ——矩形截面宽度以及T形、I形截面的腹板厚度；h、h0——截面高度和截面有效高度；h w——截面的腹板高度，矩形截面取有效高度h0；T形截面取有效高度减去翼缘高度；I形和箱形截面取腹板净高；βc——混凝土强度影响系数。

公式（5-20）和（5-21）与公式（5-10）和（5-11）也是相应衔接的。

一般要求不出现斜裂缝的钢筋混凝土深梁，应符合下列条件：(5-22)式中V tk——按荷载的标准组合计算的剪力值。

此时可不进行斜截面受剪承载力计算，但应配置分布钢筋。