受弯构件知识点

《混凝⼟结构设计原理》第四章_课堂笔记《混凝⼟结构设计原理》第四章受弯构件正截⾯承载⼒计算课堂笔记◆知识点掌握：受弯构件是⼟⽊⼯程中⽤得最普遍的构件。

与构件计算轴线垂直的截⾯称为正截⾯，受弯构件正截⾯承载⼒计算就是满⾜要求：M≤Mu。

这⾥M为受弯构件正截⾯的设计弯矩,Mu为受弯构件正截⾯受弯承载⼒，是由正截⾯上的材料所产⽣的抗⼒，其计算及应⽤是本章的中⼼问题。

◆主要内容受弯构件的⼀般构造要求受弯构件正截⾯承载⼒的试验研究受弯构件正截⾯承载⼒的计算理论单筋矩形戴⾯受弯承载⼒计算双筋矩形截⾯受弯承载⼒计算T形截⾯受弯承载⼒计算◆学习要求1.深⼊理解适筋梁的三个受⼒阶段，配筋率对梁正截⾯破坏形态的影响及正截⾯抗弯承载⼒的截⾯应⼒计算图形。

2.熟练掌握单筋矩形、双筋矩形和T形截⾯受弯构件正截⾯设计和复核的握法，包括适⽤条件的验算。

重点难点◆本章的重点:1.适筋梁的受⼒阶段，配筋率对正截⾯破坏形态的影响及正截⾯抗弯承载⼒的截⾯应⼒计算图形。

2.单筋矩形、双筋矩形和T形截⾯受弯构件正截⾯抗弯承载⼒的计算。

本章的难点：重点1也是本章的难点。

⼀、受弯构件的⼀般构造（⼀）受弯构件常见截⾯形式结构中常⽤的梁、板是典型的受弯构件:受弯构件的常见截⾯形式的有矩形、T形、⼯字形、箱形、预制板常见的有空⼼板、槽型板等；为施⼯⽅便和结构整体性，也可采⽤预制和现浇结合，形成叠合梁和叠合板。

（⼆）受弯构件的截⾯尺⼨为统⼀模板尺⼨，⽅便施⼯，宜按下述采⽤:截⾯宽度b=120, 150 , 180、200、220、250、300以上级差为50mm。

截⾯⾼度h=250, 300,…、750、800mm，每次级差为50mm，800mm以上级差为100mm。

板的厚度与使⽤要求有关，板厚以10mm为模数。

但板的厚度不应过⼩。

（三）受弯构件材料选择与⼀般构造1.受弯构件的混凝⼟等级2.受弯构件的混凝⼟保护层厚度纵向受⼒钢筋的外表⾯到截⾯边缘的最⼩垂直距离，称为混凝⼟保护层厚度，⽤c表⽰。

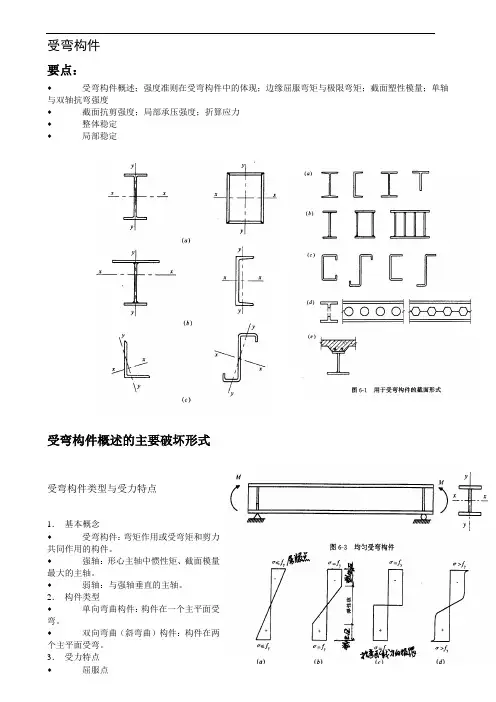
受弯构件要点：♦受弯构件概述；强度准则在受弯构件中的体现；边缘屈服弯矩与极限弯矩；截面塑性模量；单轴与双轴抗弯强度♦截面抗剪强度；局部承压强度；折算应力♦整体稳定♦局部稳定受弯构件概述的主要破坏形式受弯构件类型与受力特点1．基本概念♦受弯构件：弯矩作用或受弯矩和剪力共同作用的构件。

♦强轴：形心主轴中惯性矩、截面模量最大的主轴。

♦弱轴：与强轴垂直的主轴。

2．构件类型♦单向弯曲构件：构件在一个主平面受弯。

♦双向弯曲（斜弯曲）构件：构件在两个主平面受弯。

3．受力特点♦屈服点♦ 弹性核 ♦ 塑性区♦ 极限抗弯承载力主要破坏形式1． 截面强度破坏截面的平均应力达到屈服点f y ，截面应变迅速增加最后导致结构破坏。

通常以截面的平均应力达到屈服点f y 为轴心受压构件强度破坏准则。

2． 整体失稳破坏由于侧向干扰力或构件初始偏心等原因，受弯构件离开原来的平面，发生侧向挠曲和扭转称为受弯构件的整体失稳。

当轴力达到某一值时结构不能保持稳定的平衡状态，结构变形迅速增大开始丧失稳定性，最后导致结构破坏。

这时的轴心压力称为临界压力。

3． 局部失稳破坏构成受弯构件的板件在压应力和剪应力作用下局部出现波浪状的鼓曲变形，但轴线变形仍在弯曲平面内的的现象。

一般不一定作为构件整体破坏的判别准则。

受弯构件的截面强度强度准则1. 边缘纤维屈服准则截面上边缘处的最大应力达到屈服时即认为受弯构件的截面达到了强度极限，截面上的弯矩称为屈服弯矩。

此时构件在弹性阶段工作。

2. 全截面屈服准则一整个截面的应力达到截面承载极限强度的状态作为强度破坏的界限，此时截面上的弯矩称为塑性弯矩或极限弯矩。

3. 部分发展塑性准则将截面塑性区限制在某一范围，一旦塑性区达到规定的范围即视为强度破坏。

抗弯强度1. 缘纤维屈服准则 单向弯曲构件 双向弯曲构件 截面应力：d xn x f W M ≤=σ；d yny xn x f W M W M≤+=σ（或()()d xyn yn xn xyn x xn y xyn y yn x f I I I y I M I M x I M I M ≤--+-=2σ） 相关准则：1≤exdxM M ； 1≤+eydy exd xM M M M屈服弯矩：d xn exd f W M =；d yn eyd f W M =2. 全截面屈服准则 中性轴：⎰=dA f N y；⎰=ydA f My x；⎰=xdA f M y y相关准则：1≤pxdxM M ； 1≤+pydy pxd xM M M M极限弯矩：d pxn pxd f W M =；d pyn pyd f W M =3. 部分发展塑性准则截面应力：d exn x x f W M ≤γ； d eyny y exn x xf W M W M ≤+γγ截面塑性发展系数：ep x M M =γ相关准则：直线关系式：1≤exdx xM M γ； 1≤+eydy y exd x xM M M M γγ屈服弯矩：d xn exd f W M =；d yn eyd f W M =抗剪强度1． 单方向横向力作用 截面应力：vyd x x y f tI S V ≤=τ（vyd wy f A V ≤=τ）2． 双方向横向力作用vyd y y x x x y f tI S V tI S V ≤+=τ（或()()()vyd xyyx xxy x x y y xy y yx f tI II V I S I S V I S IS ≤--+-=2τ）局部承压强度y zw c f l t F≤=σ； 其中，分布长度y z h a l 2+= 否则，需要设置支承加劲肋。

第六章受弯构件I: 强度理论6.1 受弯构件的类型与截面6.2 受弯构件的主要破坏形式6.3 构件受弯时的截面强度6.4 构件扭转剪力中心（概念）如果要使构件仅发生弯曲而无扭转，横向荷载的作用线必须通过截面上确定的位置。

等截面构件存在一个与纵轴平行的剪力中心轴；作用在该轴上的任意横向力不会引起构件的扭转。

根据相互性定理，作用在构件上的扭矩也不会引起剪力中心轴上任意点的横向位移。

因此，在扭矩作用下，构件的剪力中心轴仍保持为直线而且位置不变；也就是说：构件的所有截面均绕此剪力中心轴转动。

剪力中心，也称为弯曲中心或扭转中心。

曲线坐标s定义：任意点O, Pnsz符合右手法则用中面代表构件；而用横截面的中线代表截面。

扇形坐标：PO ds当极点S不变时，起始原点位置的改变仅使截面上各点的扇形坐标改变一相同的常数。

Q x Q y Q x Q y00......................................(1) y x c Q x Q y tdst代表沿截面中线单位长度上的剪力，即剪力流。

By c AB x c AI ytdsI xtds如果x 和y 轴为截面的主轴，则00;y x x yI I x y I I阅读：6.3.6节：受弯构件(槽钢截面)的剪力中心对于单轴对称截面，剪力中心在截面的对称轴上；扇形惯矩和翘曲刚度截面的扇形惯矩为长度的六次方。

2,s I tds EI 截面的翘曲刚度。

6.1 受弯构件的类型与截面何为受弯构件？H钢：截面高宽比在0.5-1.0的宽翼缘工字钢；注意：强轴和弱轴之分;6.2 受弯构件的主要破坏形式2.1 受弯构件的强度破坏截面弯曲刚度主要由截面弹性核所提供；弹性核为零是说明什么？2.2 受弯构件的整体失稳理解图6-6.这种使梁丧失整体稳定的弯矩或荷载称为临界弯矩和临界荷载。

2.3 受弯构件的局部失稳导致局部失稳的机理：在横向力作用下，梁的受压翼缘与轴心压杆的翼缘类似；腹板可能有不同的受力状态，例如纯弯、纯剪等。

6.受弯构件6.1 受弯构件的形式和应用梁——承受横向荷载的实腹式受弯构件。

桁架——承受横向荷载的格构式受弯构件。

按功能分为：楼盖梁、平台梁、吊车梁、檩条、墙架梁 按制作方法分为：型钢梁、组合梁 6.2 梁的强度和刚度 一、梁的强度 1. 梁的抗弯强度实腹梁的截面正应力发展过程分为弹性、弹塑性和塑性三个阶段（2） 塑性设计允许截面部分发展塑性，塑性发展区高度a 小于等于0.125h2. 梁的抗剪强度3. 梁的局部承压强度当梁上翼缘受有沿腹板平面作用的集中荷载、且该荷载处又未设置支承加劲肋时，腹板计算高度上边缘的局部承压强度应按下式计算：轴的净截面抵抗矩轴和对—、轴为强轴）轴的弯矩（轴和绕—、y x W W x y x M M ny nx y x 1.6148，表查截面塑性发展系数，—、P y x γγ受压翼缘的厚度。

—t 。

钢材的抗剪强度设计值—腹板厚度；—毛截面惯性矩；—面对中和轴的面积矩；计算剪应力处以上毛截—用的剪力；计算截面沿腹板平面作—V w f t I S V4. 梁在复杂应力作用下的强度计算在梁的腹板计算高度边缘处，若同时受有较大的正应力、剪应力和局部压应力，二、梁的刚度梁的刚度用荷载作用下的挠度大小来衡量。

5.3 梁的整体稳定 一、梁整体稳定的概念双轴对称工字形截面简支梁纯弯，支座为夹支座（只能绕x 轴， y 轴转动，不能绕z 轴转动，只能自由挠曲，不能扭转）。

梁整体失稳的现象：侧向弯曲，伴随扭转——出平面的弯扭屈曲 二、梁整体稳定的保证规范规定，当符合下列情况之一时，不必计算梁的整体稳定：p1131.焊接工字形等截面简支梁和扎制H 型钢简支梁2. 轧制普通工字钢简支梁3. 轧制槽钢简支梁4. 双轴对称工字形等截面（含H 型钢）悬臂梁 影响梁整体稳定承载力的因素 1. 荷载的类型 2. 荷载作用位置。

＝时，取＝同号或和当＝异号时，取和当计值增大系数，验算折算应力的强度设—为负。

6.受弯构件6.1受弯构件的形式和应用 梁一一承受横向荷载的实腹式受弯构件。

桁架一一承受横向荷载的格构式受弯构件。

按功能分为：楼盖梁、平台梁、吊车梁、 按制作方法分为：型钢梁、组合梁 6.2梁的强度和刚度 一、梁的强度 1. 梁的抗弯强度 实腹梁的截面正应力发展过程分为弹性、（1）弹性设计（需要验算疲劳的梁）（2）塑性设计允许截面部分发展塑性，塑性发展区高度为了避免梁受压翼缘的局部失稳出现在强度破坏之前:t —受压翼缘的厚度。

2. 梁的抗剪强度 在主平面内受弯的梁，其抗剪强度应按下式计算：V —计算截面沿腹板平面作 用的剪力；S —计算剪应力处以上毛截 面对中和轴的面积矩; I —毛截面惯性矩； t w —腹板厚度；f v —钢材的抗剪强度设计值。

3. 梁的局部承压强度当梁上翼缘受有沿腹板平面作用的集中荷载、且该荷载处又未设置支承加劲肋 时，腹板计算高度上边缘的局部承压强度应按下式计算：檩条、墙架梁弹塑性和塑性三个阶段M x 、 W nx 、 M y —绕X 轴和y 轴的弯矩（X 轴为强轴） W ny —对X 轴和y 轴的净截面抵抗矩a 小于等于0.125h Y y —截面塑性发展系数,查 P14 8,表 6.14. 梁在复杂应力作用下的强度计算在梁的腹板计算高度边缘处，若同时受有较大的正应力、剪应力和局部压应力, 或同时受有较大的正应力和剪应力时，按下式验算折算应力：c —腹板计算高度边缘同一点上同时产生的正应力、 剪应力和局部压应力，CT 和CT c 以拉应力为正，压应力 为负。

P i—验算折算应力的强度设 计值增大系数，当O ■和％异号时，取P i = 1.2当b 和b e 同号或bc =0时，取附=1.1。

二、梁的刚度C c ， 1梁的刚度用荷载作用下的挠度大小来衡量。

5.3梁的整体稳定 一、梁整体稳定的概念 双轴对称工字形截面简支梁纯弯，支座为夹支座（只能绕 x 轴, y 轴转动，不能绕z 轴转动，只能自由挠曲，不能扭转）。