形式语言与自动机-期末考试试卷[1]

a) 构造一个接受L(r) 的-NFA（Construct a -NFA that accepts L(r)）. (3 pts)b) 给出语言L(r) 的反向的一个正规表达式（Give a regular expression for the reversal of L(r)）. (3 pts)c) 构造可以生成语言 L(r) 的一个上下文无关文法（Construct a context-free grammar generating the language L(r)）.d)e)f) (6 pts)3. (6 pts) 下图是一个扩展的两个状态的有限自动机，其中 R，S，T，和 U 是正规表达式。

可以用不同的形式给出等价于该扩展自动机的正规表达式，试给出两种这样的正规表达式。

（Give two regular expressions which describe the following generic two-state finite automata in two different ways, where R, S, T, and U are regular expressions.）4. (6 pts) 正规表达式 a*b 表示 {a, b} 上的一个语言。

试构造接受该语言的补语言的一个 DFA。

（The regular expression a*b denotes a language on {a, b}. Construct a DFA that accepts the complement of this language.）5. (8 pts) 试给出下列每个正规语言的一个正规表达式（Give a regular expression for each of the following regular languages）：a) { xwxR x, w (a + b)+ }, where (a + b)+ = (a + b) (a + b)*b) { w w {a , b}* x, y( x, y {a , b}* w = xy | y | =3 y = yR ) }w : w 2 fa; bg6. (7 pts) 下面是图灵机 M 的转移图。

一、用递归定义给出下列语言的有限描述（每题6分，共12分）1．字母表},,{c b a =∑上，以aa 结尾的所有符号串的集合。

2．字母表},,{c b a =∑上，每个a 至少有一个b 紧跟其后的所有符号串的集合。

二、文法和语言的转换（每题4分，共12分）。

1．已知语言}2,0,0,0|{>>≥>=s t n m e c c a b a L s t n m m n ，试构造相应的文法。

2．已知语言}0|{2i m n c b a L i m n ≤+≤=，试构造相应的文法。

3．已知语言}10,}1,0{{*的个数为偶数的个数为奇数中且，L ϖϖ∈=，试构造相应的文法。

三、已知上下文无关文法如下，试构造其chomsky 范式（12分）。

BabA AbAC ABa S ||→a Aa A |→A bC bBcB ||→ε||Ba Cb C →四、已知右线性文法][S G （每题4分，共12分）aA S →a bS aA A ||→(1) 构造FA(2) 确定化(3) 写出确定化后的自动机对应的正规式。

五、试用泵引理证明语言}|{k n m l d c b a L l k n m ++≠=不是正规语言（14分）。

六、构造如下文法相应的npda (14分)。

bBcA aAB aAbBB S ||→aBBc A →Ac cAb bBA B ||→七、分别给出有穷自动机)(FA 、下推自动机)(PDA 和图灵机)(TM 的物理模型，并指出它们的异同。

如有可能，给出它们相应的应用实例（12分）。

八、设计一个图灵机用于拷贝由b 构成的符号串。

确切地说，也就是构造一个机器能够执行计算ϖ0q ├ϖϖf q ，其中+∈}{b ϖ，0q 为初态，f q 为终态（12分）。

形式语⾔及⾃动机哈尔滨⼯业⼤学（中⽂版）4PDA与CFG的等价性4.1由CFG到PDA定理5.如果L是上下⽂⽆关语⾔,那么存在PDA P,使L=N(P).证明.构造PDA:设CFG G=(V,T,P′,S)且L(G)=L,构造PDAP=({q},T,V∪T,δ,q,S,?)其中δ定义:(1)对每个变元A:δ(q,ε,A)={(q,β)|A→β∈P′}(2)对每个终结符a:δ(q,a,a)={(q,ε)}那么P可以模拟G的最左派⽣,每个动作只根据栈顶的符号:如果是终结符则与输⼊串匹配,如果是⾮终结符⽤产⽣式来替换.充分性:要证明S??w=?(q,w,S)?*(q,ε,ε).那么任意w∈L(G),则存在最左派⽣S??lm w,并且除最后⼀步派⽣的w外,每次派⽣的最左句型都有xAα的形式,这⾥x∈T?,A∈V,α∈(V∪T)?.S=x1A1α1?lm x2A2α2?lm···?lm x n?1A n?1αn?1?lm x nαn=ww=x1y1=x2y2=···=x n?1y n?1=x n y n=w (q,w,S)=(q,y1,A1α1)?*(q,y2,A2α2)?*···?*(q,y n?1,A n?1αn?1)?*(q,y n,αn)=(q,ε,ε)当处于S??lmw的第i步时,若x i y i=w,有:x i A iαi??lm x i+1A i+1αi+1=?(q,y i,A iαi)?*(q,y i+1,A i+1αi+1)因为,当最左派⽣处于左句型x i A iαi时,ID为(q,y i,A iαi),如果有A i→β的产⽣式,则x i A iαi?lm x iβαi⽽x iβαi也是左句型,所以最左的变量即为A i+1,则A i+1之前x i之后的终结符记为x′,A i+1之后的记为αi+1,那么就有x i A iαi?lm x iβαi=x i x′A i+1αi+1那么由(1)P模拟A i→β的动作得到(q,y i,A iαi)?(q,y i,βαi)=(q,y i,x′A i+1αi+1)由(2)P会弹出x′,⽽y i会去掉与x′匹配的前缀,剩下的部分记为y i+1(即y i=x′y i+1),那么(q,y i,x′A i+1αi+1)?*(q,y i+1,A i+1αi+1)因此当S??lmw有(q,w,S)?*(q,ε,ε),即L(G)?N(P).必要性:要证明(q,w,S)?*(q,ε,ε)=?S??w.我们证明更⼀般的结论(q,x,A)?*(q,ε,ε)=?A??x.通过对ID转移的次数进⾏归纳证明.归纳基础:当仅需要1次时,只能是x=ε且A→ε为产⽣式.(因为即使x=a和产⽣式A→a,也需要2步才能清空栈:替换栈顶A为a,再弹出a.)所以A??ε成⽴.归纳递推:假设转移次数不⼤于n(n≥0)步时结论成⽴.当需要n+1步时,因为A是变元,其第1步转移⼀定是(q,x,A)?(q,x,Y1Y2···Y m)且A→Y1Y2···Y m是产⽣式,其中Y i是变元或终结符.⽽其余的n步转移(q,x,Y1Y2···Y m)?*(q,ε,ε)中,每个Y i不论是变元或终结符,从栈中被完全弹出时,都会消耗掉部分的x,记为x i,那么显然有x=x1x2···x m.⽽且为了清空每个Y i,需要的转移次数都不超过n,所以对i=1,2,···,m有(q,x i,Y i)?*(q,ε,ε)=?Y i??x i.再由A的产⽣式有Y1Y2···Y m??lm x1Y2···Y m??lm x1x2···Y m??lm x1x2···x m=x.A?lm因此(q,w,S)?*(q,ε,ε)=?S??w,即N(G)?L(G).⽰例为⽂法S→aAA,A→aS|bS|a构造PDA.构造PDA P=({q},{a,b},{a,b,A,S},δ,q,S,?),其中δ为δ(q,ε,S)={(q,aAA)}δ(q,a,a)={(q,ε)}δ(q,ε,A)={(q,aS),(q,bS),(q,a)}δ(q,b,b)={(q,ε)}.利⽤GNF的构造⽅法将⽂法转换为GNF格式的CFG G=(V,T,P′,S),那么PDA P的另⼀种构造⽅式为:P=({q},V,T,δ,q,S,?)为每个产⽣式,定义δ:δ(q,a,A)={(q,β)|A→aβ∈P′}.⽰例上例中的⽂法是GNF,构造PDA P′=({q},{a,b},{S,A},δ,q,S,?),其中δ为δ(q,a,S)={(q,AA)}δ(q,a,A)={(q,S),(q,ε)}δ(q,b,A)={(q,S)}.4.2由PDA到CFG定理6.如果PDA P,有L=N(P),那么L是上下⽂⽆关语⾔.证明.⽂法构造:设PDA P=(Q,Σ,Γ,δ,q0,Z0,?).那么构造CFG G=(V,T,P,S),其中V是形如[qXp]的对象和符号S的集合,其中p,q∈Q,X∈Γ,产⽣式集合P包括:(1)为Q中的每个p,构造⼀个产⽣式:S→[q0Z0p](2)如果δ(q,a,X)包括(p,Y1Y2···Y n),构造⼀组产⽣式:[qXr n]→a[pY1r1][r1Y2r2]···[r n?1Y n r n]这⾥a∈Σ∪{ε};X,Y i∈Γ;p,q∈Q;⽽r1,r2,···r n是Q中各种可能的n个状态;若i=0则构造产⽣式[qXp]→a.那么(q,w,X)?*(p,ε,ε)??[qXp]??w.充分性:ID序列(q,w,X)?*(p,ε,ε)表⽰栈弹出X⽽消耗了串w(状态从q到了p);⽽[qXp]??w 表⽰在P中经过栈符号X可以产⽣出w(状态从q到了p);设w=ax,a∈Σ∪{ε}.(1)我们要证明(q,w,X)?*(p,ε,ε)=?[qXp]??w(2)左边部分ID动作变化如果需多步完成,那么第1步时,⼀定有δ(q,a,X)包含(p,Y1Y2···Y n),(i)则第1步为(q,ax,X)?(p,x,Y1Y2···Y n)⽽其余步骤中,为弹出Y i会消耗x中的⼀部分x i,显然w=ax=ax1x2···x n;(ii)设弹出Y i之前和之后(弹出Y i+1之前)的状态分别是r i?1和r i,消耗的串是x i,这⾥i=1,2,···n且r0=p,那么其他步骤就是(r i?1,x i,Y i)?*(r i,ε,ε)(iii)⽽根据⽂法的构造规则,有[qXp]?a[pY1r1][r1Y2r2]···[r n?1Y n r n](iv)因此,只要i=1,2,···,n有(r i?1,x i,Y i)?*(r i,ε,ε)=?[r i?1Y i r i]??x i成⽴,就有[qXp]?a[pY1r1][r1Y2r2]···[r n?1Y n r n]??ax1x2···x n=w成⽴.(3)⽽左边部分ID动作变化如果仅需1步完成(或者说i=0时),由于(q,a,X)?(p,ε,ε),P只能消耗不超过⼀个的字符,即w=a(a∈Σ∪{ε}),且(p,ε)在δ(q,a,X),所以,由⽂法构造规则[qXp]→a,即(q,a,X)?(p,ε,ε)=?[qXp]?a因此(q,w,X)?*(p,ε,ε)=?[qXp]??w.必要性:略.⽰例将PDA P=({p,q},(0,1),{X,Z},δ,q,Z)转为CFG,其中δ如下:(1)δ(q,1,Z)={(q,XZ)}(4)δ(q,ε,Z)={(q,ε)}(2)δ(q,1,X)={(q,XX)}(5)δ(p,1,X)={(p,ε)}(3)δ(q,0,X)={(p,X)}(6)δ(p,0,Z)={(q,Z)}0S →[qZq ]S →[qZp ]消掉[qZp ],因与⾃⼰循环1[qZq ]→1[qXq ][qZq ][qZq ]→1[qXp ][pZq ][qZp ]→1[qXq ][qZp ]...[qZp ]→1[qXp ][pZp ]因⽣成step 2中的[qZp ]······5确定型下推⾃动机(DPDA)PDA P =(Q,Σ,Γ,δ,q 0,Z 0,F )是确定型下推⾃动机(DPDA ),当且仅当:(1)δ(q,a,X )⾄多有⼀个动作,这⾥a ∈Σ∪{ε};(2)如果δ(q,a,X )=?,那么δ(q,ε,X )=?.即?(q,a,Z )∈Q ×Σ×Γ,|δ(q,a,Z )|+|δ(q,ε,Z )|≤1.在任何情况下都不需要去选择可能的移动就是DPDA,以终态⽅式接受的语⾔也称为DCFL.虽然与PDA 不等价,但也有意义,例如语法分析器通常都是DPDA,DPDA 接受的语⾔是⾮固有歧义语⾔的真⼦集,Knuth 提出LR(k )⽂法的语⾔也恰好是DPDA 接受语⾔的⼀个⼦集,解析的时间复杂度为O (n ),LR(k )⽂法也是YACC 的基础.任何DPDA 都⽆法接受L wwr ,但是可以接受L wcwr ={wcw R|w ∈(0+1)?}.0,Z 0/0Z 01,0/101,Z 0/1Z 00,1/010,0,0/ε5.1RL 与DPDA定理7.如果语⾔L 是正则的,那么有DPDA P ,使L =L (P ).(注意是以终态⽅式接受.)DPDA P 可以不使⽤栈,⽽仅模拟DFA 即可.⼜因为L wcwr 显然是CFL,所以L (P )语⾔类真包含正则语⾔.5.2DPDA 与CFLDPDA P ⽆法识别L wwr .所以L (P )语⾔类真包含于上下⽂⽆关语⾔.5.3DPDA 与歧义⽂法定理8.如果有DPDA P ,语⾔L =L (P ),那么L 有⽆歧义的CFG.定理9.如果有DPDA P ,语⾔L =N (P ),那么L 有⽆歧义的CFG.证明略.DPDA也因此在语法分析中占重要地位.但是并⾮所有⾮固有歧义CFL都会被DPDA 识别.例如L wwr有⽆歧义⽂法S→0S0|1S1|ε.5.4语⾔间的关系a nb nc nww Rwcw Ra?b?。

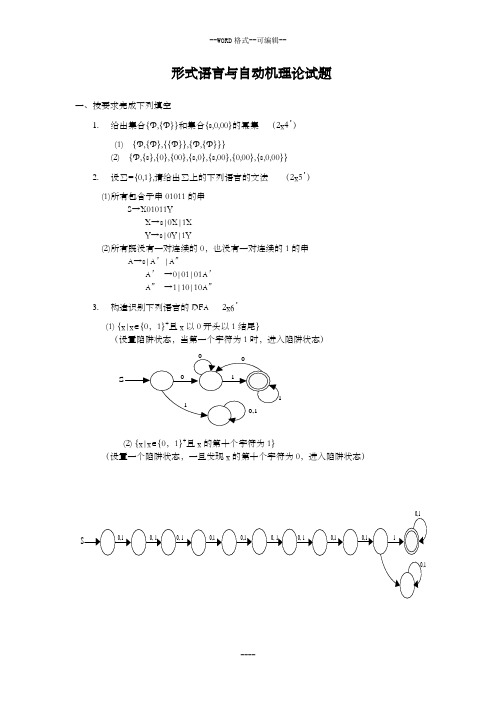
形式语言与自动机理论试题一、按要求完成下列填空1.给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集 （2x4'）(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}2.设∑={0,1},请给出∑上的下列语言的文法 （2x5'）(1)所有包含子串01011的串 S →X01011YX →ε|0X|1X Y →ε|0Y|1Y(2)所有既没有一对连续的0，也没有一对连续的1的串 A →ε|A ’|A ”A’ →0|01|01A ’ A ” →1|10|10A ”3.构造识别下列语言的DFA 2x6'(1) {x|x ∈{0，1}+且x 以0开头以1结尾}（设置陷阱状态，当第一个字符为1时，进入陷阱状态）1S110,10 (2) {x|x ∈{0，1}+且x 的第十个字符为1}（设置一个陷阱状态，一旦发现x 的第十个字符为0，进入陷阱状态）1S0,10,10,10,10,110,0,10,10,10,10,1二、判断（正确的写T ，错误的写F ） 5x2'1.设1R 和2R 是集合{a,b,c,d,e}上的二元关系，则3231321)(R R R R R R R ⊆( T )任取(x.,y),其中x,y },,,,{e d c b a ∈，使得321)(),(R R R y x ∈。

)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒2.对于任一非空集合A ，Φ⊆A2 ( T ) 3.文法G ：S A|AS A a|b|c|d|e|f|g 是RG ( F ) 4.3型语言2型语言1型语言0型语言 ( T )5.s （rs+s ）*r=rr *s （rr *s ）* ( F )不成立，假设r,s 分别是表示语言R ，S 的正则表达式，例如当R={0}，S={1}, L(s(rs+s)*r)是以1开头的字符串，而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*) 所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立三、设文法G 的产生式集如下，试给出句子aaabbbccc 的至少两个不同的推导（12分）。

大学语言类期末考试题及答案一、选择题（每题2分，共20分）1. The word "phenomenon" is most closely related to which of the following?A. PhenomenalB. PhenomenalizeC. PhenomenologyD. Phenomenonize答案：C2. Choose the correct translation for "ephemeral" in Chinese.A. 永恒的B. 短暂的C. 永恒的D. 永恒的答案：B3. Which of the following is NOT a function of language?A. CommunicationB. ExpressionC. EntertainmentD. Storage答案：C4. The phrase "to be on cloud nine" typically means:A. To be very high upB. To be very happyC. To be very sadD. To be very confused答案：B5. The term "dialect" refers to:A. A type of foodB. A type of musicC. A type of languageD. A type of clothing答案：C6. What is the past tense of "write"?A. WroteB. WritesC. WritingD. Writed答案：A7. The word "altruism" is opposite to:A. EgotismB. AltruismC. EgalitarianismD. Egalitarian答案：A8. The idiom "to break the ice" means:A. To start a conversationB. To make a decisionC. To end a relationshipD. To make a mistake答案：A9. The word "pragmatic" is most closely associated with:A. PracticalB. TheoreticalC. ImaginativeD. Emotional答案：A10. The phrase "to be in the pink" means:A. To be very wellB. To be very tiredC. To be very angryD. To be very sad答案：A二、填空题（每空2分，共20分）11. The word "____" means "a person who is very careful with money."答案：Miser12. The phrase "____" is used to describe someone who is very cautious.答案：Play it safe13. "____" is the term used to describe a person who is always ready to help others.答案：Good Samaritan14. The word "____" can be used to describe a person who is very talkative.答案：Garrulous15. "____" is a phrase that means to make a situation better.答案：Improve16. The word "____" is used to describe a person who is very honest.答案：Candid17. "____" is a term that refers to the study of languages.答案：Linguistics18. The phrase "____" means to be very careful with one's words.答案：Choose one's words carefully19. "____" is the term used to describe a person who is very organized.答案：Methodical20. The word "____" can be used to describe a person who is very sensitive to criticism.答案：Thin-skinned三、阅读理解（每题5分，共30分）阅读下面的短文，然后回答问题。

形式语言与自动机理论_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.令字母表【图片】, 则克林闭包【图片】中元素的长度为？参考答案:只能是有限的2.由字符0和1构成且含有奇数个1的DFA，至少需要几个状态？参考答案:23.双栈PDA可以接受任意图灵机接受的语言。

参考答案:正确4.由某字母表【图片】中的字符构成的全部正则表达式的集合，也可以看做是一个语言，则该语言为：参考答案:上下文无关语言5.由字符0和1构成且含有奇数个1和偶数个0的DFA，至少需要几个状态？参考答案:46.字符串的长度可以是任意的，那么也可以是无穷长的。

参考答案:错误7.设【图片】和【图片】是字母表【图片】上的任意语言且【图片】是无穷的，则两个语言的连接【图片】一定是无穷的。

参考答案:错误8.每一个有穷的语言都是正则语言。

参考答案:正确9.任何正则语言都是上下文无关语言。

参考答案:正确10.任意有穷集合的克林闭包一定是无穷集合。

参考答案:错误11.递归可枚举语言是可判定的语言。

参考答案:错误12.任何有限的语言都是上下文无关语言。

参考答案:正确13.NFA处于某个状态q且输入某字符a时，如果状态转移函数未定义，则NFA会：参考答案:停止自动机的运行，并拒绝该串。

14.有穷自动机有了空转移（不消耗输入串的状态跳转）, 改变了它识别语言的能力。

参考答案:错误15.对同一个语言，可能存在两个不同的有穷自动机识别。

参考答案:正确16.带有空转移的非确定有穷自动机中，对于某一个状态，是否可以同时存在“对某字符a的非确定性”和“空转移”？参考答案:可以。

17.图灵机是算法的好模型。

参考答案:错误18.确定的图灵机与非确定的图灵机等价。

参考答案:正确19.由字符0和1构成且含有偶数个1的DFA，至少需要几个状态？参考答案:220.如果一个语言是不可判定的，那么它的补也一定是不可判定的参考答案:错误21.确定的有穷自动机中，“确定的”含义是：参考答案:状态转移是确定的22.由字符0和1构成且长度为偶数的全部字符串的DFA，至少需要几个状态？参考答案:223.集合的克林闭包与正比包一定不相等参考答案:错误24.设【图片】是字母表【图片】上的任意语言，则语言【图片】的闭包【图片】一定是无穷的。

形式语言与自动机期末复习题及答案（一）1.有图灵机 M=(Q, ∑, Γ, δ,q 0 , B , F) 接受语言{w t w│w ∈{a, b}*}，按照下图说明其接受过程。

（本题15分 ）[q 1[q 6,B]答：abtab 的分析过程：[q 1,B]abtab├a [q 2,a]btab├ab [q 2,a]tab├abt [q 3,a]ab├ ab [q 4,B]tab├a [q 5,B]btab├[q 6,B]abtab├a [q 1,B]btab ├ab [q 2,b]tab├abt [q 3,b]ab ├abta [q 3,b]b ├abt [q 4,B]ab├a [q 5,B]btab ├ab [q 7,B]tab ├abt [q 8,B]ab├abta [q 8,B]b ├abtab [q 8,B]B├abta [q 9,B]b 接受abtab√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√2.简述《形式语言与自动机》课程的主要内容。

(本题10分)答：语言的文法描述；RL （RG 、FA 、RE 、RL 的性质 ）；CFL （CFG(CNF 、GNF)、PDA 、CFL 的性质）；TM （基本TM 、构造技术、TM 的修改）；CSL （CSG 、LBA ）。

3.简述《形式语言与自动机》课程的学习目的和基本要求。

(本题10分) 答：本专业人员4种基本的专业能力：计算思维能力、算法的设计与分析能力、程序设计和实现能力、计算机软硬件系统的认知、分析、设计与应用能力。

其中计算思维能力包括：逻辑思维能力和抽象思维能力、构造模型对问题进行形式化描述、理解和处理形式模型。

本课程应使学生掌握如下知识：正则语言、下文无关语言的文法、识别模型及其基本性质、图灵机的基本知识。

锻炼培养如下能力：形式化描述和抽象思维能力、了解和初步掌握“问题、形式化描述、自动化（计算机化）”这一最典型的计算机问题求解思路。

《形式语言与自动机》期末测试题《形式语言与自动机》期末测试题（规定时间：2小时）学号姓名1. (12 pts)选择填空（多选）：(a) 由正规表达式a*定义的语言；A,C（或只回答C）(b) 语言{a m b m∣m ≥0} ；B(c) 语言{a m b m c m∣m ≥0} ；D(d) 语言{a m b n c m∣m,n ≥0} ；B(e) 对角化（diagonalization）语言L d；F(f) 通用语言（universal）语言L u；E供选择的答案：A. 是某个有限状态自动机的语言；B. 是某个下推自动机的语言, 但不是任何有限状态自动机的语言；C. 是某个有限状态自动机的语言,但不是任何空栈接受方式的确定下推自动机的语言；D. 是某个可停机的图灵机的语言, 但不是任何下推自动机的语言；E. 是某个图灵机的语言, 但不是任何可停机的图灵机的语言；F. 不是任何图灵机的语言.2. (7 pts)图灵机（{ q0, q1, q2, q3 }, { 0,1 }, { 0,1,B }, δ, q0, B, {q3 }）有如下转移规则：δ（q0, 0）=（q1,1, R）δ（q1, 1）=（q2, 0, L）δ（q2, 1）=（q0, 1, R）δ（q1, B）=（q3, B, R）给出从初始ID q00110开始,该图灵机可以到达的完整的ID序列, 直到它停机.3. (12 pts)设有四个语言（或问题）A，B，C 和D. 这些语言可以是，也可以不是递归可枚举语言，但已知如下条件：（此题出得不好）i. A 可以归约到B（不一定是多项式时间归约，下同）；ii. B 可以归约到C；iii. D 可以归约到C；对于以下6个命题，分别指出它们是“真”，或是“假”，或是“不能确定”：(a) A是递归可枚举的但不是递归的，而C 是递归的. 假（A 不是递归的与C是递归的不可能同时成立）(b) B不是递归的，而D 是递归可枚举的. 不能确定(c) A的补不是递归可枚举的，而B 的补是递归可枚举的. 不能确定(d) B的补不是递归的，而C 的补是递归的. 假(e) 如果 A 是递归的，那么 B 的补是递归的. 不能确定(f) 如果 C 是递归的，那么 D 的补是递归的. 真4. (11 pts) 文法 G 的产生式集合为：S →AS ∣b, A →BB ∣a ∣b,B →BA ∣a . 下面的左图表示对于文法 G 和字符串 ababb 应用 CYK 算法时所构造的表，各集合与表元素符号之间的对应关系可参照右边的图. 试问(a) 计算 X 15 时与哪几对表元素相关？ (5 pts)(b) X 15 = ？ (5 pts) {S,A,B}(c) 是否有ababb ∈ L(G)? (1 pt) Ye sX 15X 14X 13X 12X 11X 25X 24X 23X 22X 35X 34X 33X 45X 44X 55a 1a 2a 3a 4a 5a b a b b {S,B }{S,A,B }{S,A }{A,B }{S }{A,B }{S,B }φ {A,B }{S,B }{S,A }{S,A }{S }{S }X 155. (8 pts) 对于正规语言和上下文无关语言两类语言，分别指出下列四个问题是否可判定的：(a) 给定该语言类中的任一语言 L ，判定 L 是否为空？都可以(b) 给定该语言类中的任一语言 L 和任何字符串 w ，判定 w 是否属于 L ？. 都可以 (c) 给定该语言类中的语言 L 和 M ，判定 L 是否与M 相等？. 对正规语言可以，对上下文无关语言不可以对于递归语言和递归可枚举语言两类语言，分别指出上述问题（b ）是否可判定的：对递归语言可以，对递归可枚举语言不可以6. (15 pts) 对下面描述每一对语言，指出以下 4 种选择中的哪一个正确表达了它们之间的关系：（1）?（2）：语言（1）是语言（2）的真子集；（1）?（2）：语言（2）是语言（1）的真子集；（1）=（2）：语言（1）和语言（2）相等；（1）？（2）：语言（1）和语言（2）之间没有包含关系，即（1）中的某些串不在（2）中，（2）中的某些串不在（1）中.(a) （1）产生式集为S →0S1∣1S0∣ε 的 CFG 的语言.（2）正规表达式 (0+1)* 的语言.（1）?（2）. (2) generates all strings of 0's and 1's, while (1) doesn't generate strings like 11, or any odd-length string.(b)（1）以终态方式接受的PDA（{ p，q }，{ 0,1 }，{ X,Z }，δ，q，Z，{ p }）的语言，其中δ转移包括：δ(q,0,Z)=(q,XZ), δ(q,0,X)=(q,XX), δ(q,1,X)=(p,ε), δ(p,1,X)=(p,ε).（2）产生式集为S→0S1∣0S∣ε的CFG的语言.（1）?（2）. These almost look the same. (2) is the set of strings of the form 0n1m such that 0 ≤ m ≤ n. However, the PDA of (1) cannot reach state p without reading at least one 0 and one 1, so it accepts the set of strings of the form 0n1m such that 1 ≤ m ≤ n .(c) （1）产生式集为S→AS∣SB∣ε，A→0 和B→1 的CFG的语言.（2）正规表达式0*1* 的语言.（1）=（2）(d) （1）正规表达式(0+1)*11(0+1)* 的语言.（2）正规表达式(0*1*11)*0*110*1* 的语言.（1）?（2）. (1) is all strings of 0's and 1's with two consecutive 1's. (2) misses some of these strings, e.g., something ending with 110101(e)（1）NFA（{ p，q }，{ 0,1 }，δ，q，{ q }）的语言，其中转移函数δ为：δ(q,0)={p }, δ(q,1)=φ, δ(p,0)={p,q}, δ(p,1)={p}.（2）产生式集为S→AS∣ε，A→0B 和B→ 0B∣1B ∣0 的CFG的语言.（1）=（2）. Both define the language of regular expression (0(0+1)*0)*.7. (10 pts)利用上下文无关语言的闭包运算可以证明某些语言是或不是上下文无关语言.试证明{a n b n+2∣n ≥0} 为上下文无关语言，而{a n b n-i c i d n-j e j∣i,j≤n} 不是上下文无关语言（提示，已知{0n1n∣n ≥0} 为上下文无关语言，而{0n1n2n∣n ≥0} 不是上下文无关语言）.前者可以用连接和同态运算；后者可以用同态运算。