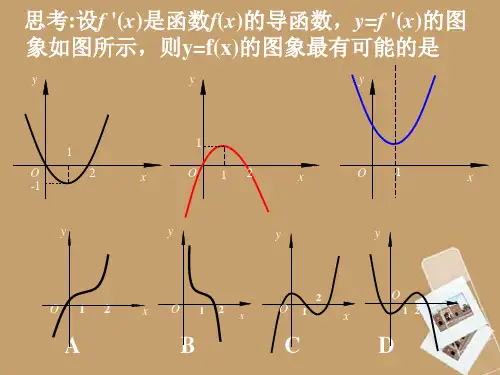
习课件——导数的应用(三次函数)

3a 3a
知识点2 切线条数 切点的个数
数学思想方法 数形结合，特殊与一般，化归转化
思考
一般情形的证明
对于对称问题，在函数中讲到了很 多，你能用所学知识证明一般三次函数 f (x) ax3 bx2 cx d (a 0) 的对称中心 是 ( b , f ( b ))的这个结论吗？
3a 3a
g(x) x3 3x2 2x 1 (1,1)
x y20
过对称中心的切线只有1条
上下区域 1条
左右区域 3条
切线上（除对称中心） 2条
曲线上（除对称中心） 2条
一般情形
小结
知识点1 对称中心
三次函数有唯一的对称中心，对称中心的横 坐标与其导函数顶点的横坐标相同. ( b , f ( b ))
应用导数研究三次函数
图像的对称性及切线条数
湖北省黄冈中学 袁小幼
函数 y x3图像的对称性
函数 y 的x3图像关于（0，0）对称.
三次函数的图像有唯一的对称中心，对称中 心的横坐标与其导函数顶点的横坐标相同.
一般三次函数图像的对称性
三次函数 f (x) ax3 bx2 cx d (a 0)图像 的对称中心是什么?
f (x) 3ax2 2bx c 3a(x b )2 c b2
3a
3a
( b , f ( b )) 3a 3a
三次函数在对称中心处的切线
函数 g(x) x3 3x2 2x 1 过对称中心 (1,数图像切线条数的探究
同样的，你能证明切线条数的一般 性结论吗？
谢 谢！

f′(x) －
0
＋
f(x) 4
极小值－43
1
从上表可知，函数 f(x)＝13x3－4x＋4 在[0，3]上有极小值为－43，
最大值为 4，最小值为－43.
若函数 f(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，则 f(x) 在[a，b]上必有最大值和最小值，其最值一定在极值点处或区间 端点处取得．因此在求闭区间[a，b]上连续，开区间(a，b)内可导 的函数的最值时，可将过程简化，即不用判断导数为零的点是极 大值点还是极小值点，直接将极值与端点的函数值进行比较，就 可判断出函数的最大(小)值．对于开区间(a，b)内可导的函数(定 义域为开区间或半开半闭区间)求最值时，除求出函数的极大值、 极小值外，还应考虑函数在区间端点处的极限值或画出函数的大 致图象，再判定函数的最大(小)值，否则会犯错误．但定义在开 区间(a，b)内的可导函数，如果只有一个极值点，该极值点必为 最值点．
求下列各函数的最值． (1)f(x)＝4x3＋3x2－36x＋5，x∈[－2，2]； (2)f(x)＝x3－3x2＋6x－2，x∈[－1，1]． 解：(1)f′(x)＝12x2＋6x－36＝6(2x2＋x－6)， 令 f′(x)＝0，解得 x1＝－2，x2＝32. 又 f(－2)＝57，f32＝－1145，f(2)＝－23， 所以函数 f(x)的最大值为 57，最小值为－1145.
(2)由(1)的分析知 y＝f(x)的图象的大致形 状及走向如图所示．所以，当 5－4 2＜a ＜5＋4 2时，直线 y＝a 与 y＝f(x)的图象 有三个不同交点，即方程 f(x)＝a 有三个 不同的实根．
用求导的方法确定方程根的个数，是一种很有效的方法．它通 过函数的变化情况，运用数形结合思想来确定函数图象与 x 轴 的交点个数，从而判断方程根的个数．

(2)f(0)=0,f(3)=18, 则f(x)min=-2，f(x)max=18
例2、 已知函数 f (x) x3 3x, x R
变式一 若关于x的不等式 f (x) k 在[0,3]上恒成立， 求实数k的取值范围。
分析 (1) f (x) 3x2 3， 令 f (x) 0,得x=±1. f(x)随x变化：
或
－c32ab23
a 2,b 9, c 12
3a
例2、 已知函数 f (x) x3 3x, x R
(1)求函数 f (x) 的单调区间与极值； (2)求 f (x)在x [0,3]上的最值； (3)在点A(2,2)处作曲线y=f(x)的切线,求切线方程。 (4)过点A(2,2)作曲线y=f(x)的切线,求切线方程。 分析 (1) f (x) 3x2 3， 令 f (x) 0,得x=±1. f(x)随x变化：
You Know, The More Powerful You Will Be
结束语
当你尽了自己的最大努力时，失败也是伟大的， 所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人：XXXXXX 时 间：XX年XX月XX日
2 1
-1 o
-2
y =a
x
(2)f(0)=0,f(3)=18, 则f(x)min=-2，f(x)max=18
例3 已知函数 f (x) x3 ax2 x 在 (, 1] 上是增函数,
求实数a取值范围
变式 已. 知函数 f (x) x3 ax2 x 在(, 1],[1, ) 上均递增
求实数a取值范围

x [3， )有三个零点，求实数t的取值范围。
2.6【畅所欲言------说反思】
出题者的意图想考我们求导知识，极值与零点概念、分 类讨论思想，数形结合思想等，所以我们平时要加强这 方面知识，同时它也反应出用导数知识解决函数问题的 基本题型与基本步骤，其它的可根据个人依不同角度总
结。你体会到了吗？比如：
2.3【各抒己见------说解法】(1)
例1：已知函数f(x)=(x2+ax+a)gex, (a R)。
（1）求函数f(x)的单调区间与极值；
2.3【各抒己见------说解法】（2)
例1：已知函数f(x)=(x2 +ax+a)gex, (a R)。
(2)设g(x)=f (x) t, (t R, a 2), 若函数g(x)在
x [3， )有三个零点，求实数t的取值范围。
分类讨论是否重复或遗漏？ 定义域优先考虑了吗？ 隐含条件注意了吗？ 分类讨论后“综上所述”了吗？ 计算过程都正确吗？ 有谁可以把错解拿来辨析吗？ 有没有其他方法？
2.5【引申拓展------说变式】 例1：已知函数f(x)=(x2+ax+a)gex, (a R)。 （1）求函数f(x)的单调区间与极值； (2)设g(x)=f (x) t, (t R, a 2),若函数g(x)在
f(-a)
f(-3)
-2 -3 -a
f(-2)
a2 (3) 3 a 解得a ？ 至多两个零点，不合题意
f(-a)
f(-3)
-2 -a -3
f(-2)
2.3【各抒己见------说解法】（3）
2.4【精益求精------说检验】
例1：已知函数f(x)=(x2+ax+a)gex, (a R)。 （1）求函数f(x)的单调区间与极值； (2)设g(x)=f (x) t, (t R, a 2),若函数g(x)在

聚焦中考——语文 第五讲
表达方式与记叙的顺序
• （2013·荆门）阅读下文，完成习题。 • ①那天下午6点多，该上公交车的人早已上了车，唯独有个小女孩，在车
门边来回徘徊。眼看着司机就要开车了，我在想，这小女孩肯定是没钱 上车。 ②“小姑娘，上车吧，我帮你交车票钱。”当看到我为她刷完卡后，她 随即上了车，说了声“谢谢阿姨”，一时脸蛋儿全红了。近距离一看， 才发现，小女孩左侧脸上有颗小痣。几天前的一幕不由浮现眼前—— ③送走远方的朋友，我从火车站迎着风雨赶到就近的公交车站台，已是 下午5点多。这时正是下班高峰期，来了几辆公交车，我总也挤不上去。 雨还在急速地下着，人还在不断地涌来。当又一辆10路公交驶来后，我 和许多人一起先往前门挤，但挤不上去。等司机发话后，才从后门好不 容易挤上车。车内人头攒动，人满为患。这人贴人的，身体若要移动一 下都难。正感叹着，我突然感觉好像有一件事还没做。是什么事呢？哦， 对了，没买车票。本想挤到前面去交车钱，可大伙儿都好像没事人一样 在原地一动不动，根本挤不过去。见此情形，司机也没说什么，这样， 我也就心安理得地和大家一样坐了一次免费的公交车。
本题在当年的高考中，出错最多的就是将第(1)题 的 a＝4 用到第(2)题中，从而避免讨论，当然这是错误的．
【互动探究】 1．(2011 届广东台州中学联考)设 f′(x)是函数 f(x)的导函数，
将 y＝f(x)和 y＝f′(x)的图象画在同一直角坐标系中，不可能正确 的是( D )
考点2 导数与函数的极值和最大(小）值
高考数学一轮复习导数在函数中的应用-教学课件
第2讲 导数在函数中的应用
考纲要求
考纲研读
1.了解函数单调性和导数的关系；能利用 1.用导数可求函数的单 导数研究函数的单调性，会求函数的单调 调区间或以单调区间为 区间(对多项式函数一般不超过三次)． 载体求参数的范围．

高中数学《导数的概念》公开课优秀课件标题：高中数学《导数的概念》公开课优秀课件尊敬的各位老师，大家好！今天我们将一起学习高中数学中一个非常重要的概念——导数的概念。

这个概念在微积分学中占据了重要的地位，对于我们理解函数的变化率，以及在科学、工程、经济和计算机科学等领域都有广泛的应用。

一、导数的定义首先，让我们来看看导数的定义。

假设有一个函数f(x)，在某一点x0的附近取一系列的点，这些点的横坐标是x0+Δx。

那么，函数f(x)在点x0的导数就是这一系列点的纵坐标f(x0+Δx)与横坐标之商的极限，记作f'(x0)。

二、导数的几何意义从几何意义上来看，导数表示函数在某一点处的切线的斜率。

当我们把函数在x0附近的点沿着横坐标逐渐移动时，该点的纵坐标会相应地变化，这个变化率就是导数。

三、导数的应用导数的应用非常广泛，它可以用来解决很多实际问题。

例如，在物理学中，导数被用来描述物体的运动学和动力学问题，如速度和加速度；在经济学中，导数被用来分析成本、收益和价格的变化；在计算机科学中，导数被用来研究图像处理和人工智能的问题。

四、导数的计算导数的计算有很多方法，其中最常见的方法是使用导数的定义。

我们可以根据定义来推导出一些基本的导数公式，如常数函数的导数为0，幂函数的导数与其指数有关，三角函数的导数与其角度有关等。

五、总结与复习今天我们学习了导数的概念和计算方法。

导数是微积分学的基础，它描述了函数在某一点处的变化率。

通过学习导数的定义和基本公式，我们可以解决很多实际问题。

六、作业与扩展阅读为了加深对导数概念的理解，请大家完成以下作业：1、复习并熟练掌握导数的基本定义和公式；2、自行寻找并解决一到两个与导数相关的问题（可以从物理、经济或计算机科学等领域寻找）。

同时，我推荐大家阅读《微积分的概念》这本书，作者是著名的数学家Richard Courant。

这本书对微积分的概念有深入且生动的解释，对于我们深入理解导数的概念非常有帮助。

2 1
-1 o
-2
y =a
x
(2)f(0)=0,f(3)=18, 则f(x)min=-2，f(x)max=18
例3 已知函数 f(x)x3ax2x 在 (, 1] 上是增函数,
求实数a取值范围
变式 已. 知函数 f(x)x3ax2Байду номын сангаас在(,1],[1,)上均递增
求实数a取值范围
,
.
课堂小结 一 知识框架
三 次
导数
三次函数
函
的图象
数
二 数学思想
转化与化归思想，数形结合，从特殊到一般， 分类讨论等
三次函数f(x)=ax3+bx2+cx+d(a≠0)的图象
a>0
Δ>0
Δ≤0
a<0
Δ>0
Δ≤0
x x1 x2
x x0
x x1 x2
x x0
人有了知识，就会具备各种分析能力， 明辨是非的能力。 所以我们要勤恳读书，广泛阅读， 古人说“书中自有黄金屋。 ”通过阅读科技书籍，我们能丰富知识， 培养逻辑思维能力； 通过阅读文学作品，我们能提高文学鉴赏水平， 培养文学情趣； 通过阅读报刊，我们能增长见识，扩大自己的知识面。 有许多书籍还能培养我们的道德情操， 给我们巨大的精神力量， 鼓舞我们前进。
(1)求函数 f ( x ) 的单调区间与极值； (2)求 f (x)在x[0,3]上的最值； (3)在点A(2,2)处作曲线y=f(x)的切线,求切线方程。 (4)过点A(2,2)作曲线y=f(x)的切线,求切线方程。 分析 (1) f(x)3x2 3， 令 f (x) 0,得x=±1. f(x)随x变化：
浙江省温州市龙湾中学高一数学导数在三次函数中的运用课件

例4. 已知曲线C: y=4ax3+x, 过点Q(0,-1)作C的切线 l, 切点为P. (1) 求证：不论a怎样变化, 点P总在一条定直线上; (2) 若a>0, 过点P且与l垂直的直线与x轴交于点T, 求|OT|的最小值(O为原点). (1)切点Ｐ总在直线y=x+1/2上 (2)|OT|的最小值为2+ 6.
△>0 a≤0 △>0
a>0
a<0
a>0
a<0
f(x)=0有且仅有一个实根， f(x)的极大值小于0或极小值大于 y=f(x）与x轴有且仅有一个 0 f(x)=0有且仅有一个实根。 f(x)的极大值等于0或极小值等于 交点。
f(x)的极大值大于0且极小值小于 0 ，f(x)=0有且仅有三个不等实 根。y=f(x）与x轴有且仅有三个 交点。
综上所述 a 的取值范围为 ，5
3
2
三次函数---导数应用中一颗璀璨的明珠
导 数 及 其 应 用
函数的 单调性
极值与 最 值 切线 问题
三次函数 的图象
三 次 函 数
三次函数 的性质 与三次方 程的关系
导 数
课 堂 小 结
感悟数学
发现数学
应用数学
三次函数---导数应用中一颗璀璨的明珠
思考题：
例3．设a为实数,函数f(x）=x3-x2-x+a (1) 求f(x)的极值. (2) 当a在什么范围内取值时, 曲线y=f(x)与x轴仅 有一个交点.
(1)f(x)的极大值是f(-1/3)=5/27+5, 极小值是 f(1)=a-1. (2)当a (-∞,-5/27)U(1,+∞)时, 曲线y=f(x)与x 轴仅有一个交点.

5 5 ， 极小值-1， 当 a 或 a 1 时 27 27
函数 g ( x ) x 3 x 2 x 与函数 y a 只有一个交点， 所以当 a ( ，
5 ) (1， ) 时，曲线 y f ( x ) 与 x 轴仅有一个交点。 27
本课小结
3
几何画板
f ( x) ax bx cx d (a 0)
3 2
2 f ( x) 3ax 2bx c
4b -12ac 4(b -3ac)
2 2
a 0, 0
y y
x1 O
x2
x2 x x1
f ( x) ax bx cx d (a 0)
1 )上 3
5 ) (1， ) 时，曲线 y f ( x ) 与 x 轴仅有一个交点。 27
方法二： 将 f ( x ) 与 x 轴交点问题转化为函数 g ( x ) x 3 x 2 x 与函数 y a 的 交点个数问题
y=-a
y
5 27
x
-1
易求函数 g ( x ) x 3 x 2 x 的极大值
方法一: 转化为a>0利用图像 方法二: 利用图象
例 3 设 a 为实数，函数 f ( x ) x 3 x 2 x a 。 （Ⅰ）求 f ( x ) 的极值； （Ⅱ）当 a 在什么范围内取值时，曲线 y f ( x )与x 轴仅有一个交点。
解法分析：
1 5 对于问题（Ⅰ）易得 f(x)的极大值是 f ( ) a ，极小值是 f (1) a 1 3 27
三次函数图像与性质
复习:二次函数的图象与性质
函数 二次函数y=ax2+bx+c（a、b、c是常数a≠0） a>0

导数在三次函数中的应用教学设计一.教学内容分析三次函数32()(0)f x ax bx cx d a =+++≠ 是高中数学利用导数研究函数单调性、极值、最值等内容的一个重要载体，是应用二次函数图像和性质的重要素材. 本课立足于一道题目，建构三次函数图像特征，对零散知识进行串联，运用变式，探究解决问题的通性通法，同时根据问题的自身特点寻求简化解法，培养提高学生思考问题分析解决问题的能力. 二．学生学习情况分析学生已经学习了导数在研究函数单调性及其极（最）值的应用，掌握了利用导数求函数单调区间、求极值最值、求切线方程，求参数取值范围的一般方法.三．教学目标导数及其应用主要两个方面：一是利用导数研究函数的单调性，二是用导数研究函数的极（最）值，三次函数是一类重要的函数，在高考中占有重要地位，因此以三次函数为载体，掌握利用导数研究三次函数单调性，求极值最值的通性通法，巩固数形结合、分类讨论、化归数学思想的应用.四．教学重点与难点教学重点：用导数解决三次函数的单调性、极值最值、切线方程等问题教学难点：分类讨论,数形结合，化归思想在解决问题中的综合应用五．教学过程一、课前练习1.3()31=--f x x x 的单调递减区间为2. 322()3=+++f x x ax bx a 在1=-x 时有极值0，则-=a b3. 3()1=--f x x ax 在(2,)-+∞上既有极大值又有极小值，则a 的取值范围是4. 3()3=-+f x x x a 有三个零点，则a 的取值范围二、问题分析问题13()31=-+f x ax x ，讨论()f x 的单调性，做出大致图像.32()0f x ax bx cx d a =+++>（）类似于二次函数的图像和性质表：232(0）=++>ax bx c a问题2、已知函数3()31=-+f x ax x 在(1,1)-单调递减，求实数a 的取值范围变式：已知函数3()31=-+f x ax x 单调递减区间为(1,1)-，求实数a 的取值范围问题3：已知函数3()31=-+f x ax x 在(1,2)上不单调，求实数a 的取值范围问题4：已知函数3()31=-+f x ax x 在[1,2]上存在单调增区间，求实数a 的取值范围问题5： 设函数f (x )＝ax 3－3x ＋1 (x ∈R )，若对于x ∈[－1，1]，都有f (x )≥0，则实数a 的值为__________________三、小结反思通过本节课学习谈谈你的收获 032>-ac b 032≤-ac b图像()0f x =根的个数与x 轴的交点单调性极值。

课本练习
思考,已知函数 在区间[1,5] 思考,已知函数f(x)=x2-2(m-1)x+4在区间 在区间 内的最小值为2, 内的最小值为 ,求m的值 的值
导数的定义
导数的几何意义
导数
求导公式与法则
多项式函数的导数
函数单调性 导数的应用 函数的极值 函数的最值
基本练习 1,曲线 ,曲线y=x4-2x3+3x在点 在点P(-1,0)处的切线的 在点 , 处的切线的 斜率为( 斜率为 ) (A) –5 (B) –6 (C) –7 (D) –8 2,函数y=x100+2x50+4x25的导数为 ) ,函数 的导数为( (A)y'=100(x99+x49+x24) (B) y'=100x99 (C) y'=100x99+50x49+25x24 (D) y'=100x99+2x49
定义法 公式法
练习: 练习: 1,求下列函数的导数 ,
)(x (1)y=(x2-3x+2)( 4+x2-1) ) ( )( ) (2)y=(x/2+t)2 ) ( )
2,设f(x)=ax3-bx2+cx,且f /(0)=0, , ( ) , ) , f /(1)=1,f /(2)=8,求a,b,c ) , ) , , , 3,抛物线f(x)=x2-2x+4在哪一点处的 ,抛物线 ( ) 在哪一点处的 切线平行于x轴 在哪一处的切线与x轴的 切线平行于 轴?在哪一处的切线与 轴的 交角为45 交角为 0?
5, 求导的公式与法则 , 求导的公式与法则——
/
(C ) = 0 n / n 1 * ( x ) = nx (n ∈ N )

构造
()
g(x)= ;
e
(4)对于f(x)满足x2f'(x)>1,构造函数F(x)=f(x)+
1
.

对点训练1(1)已知函数f(x)的导函数为f'(x),且f'(x)<f(x)对任意的x∈R恒成
立,则(
)
A.f(1)<ef(0),f(2 020)>e2 020f(0)
B.f(1)>ef(0),f(2 020)>e2 020f(0)
f(x)=x-2ex 上和直线 g(x)=2-x 平行的切线方程,由 f'(x)=1-2ex=-1,得 x=0,所以
切点坐标为(0,-2),所以(a-c)2+(b-d)2 的最小值为
|0-2-2|
1+1
2
=8.
规律方法 解题中若遇到比较大小及有关不等式、方程及最值之类的问题,
设法建立起目标函数,并确定变量的限制条件,通过研究函数的单调性、最
3
1
2
,即
x=
,y=
时,等号成立,因为不等式
+
≥m
对任意的正实数

4
2


x,y 恒成立,所以
8
m≤ ,所以实数
3
m
8
的最大值为 .
3
b

,e e 这三个数先取自然对数再除以
a
(2)对 a ,b
ln

=

ln ln e e

,

1
e
= =
=
ln

=
ln ln
,


=

B．长．长度不变，但顺序改变
精典例题
5.诱发突变与自然突变相比，正确的是 D
A．都是有利的 B．都是定向的 C．都是隐性突变 D．诱发突变率高
精典例题
4、人类能遗传给后代的基因突变常
发生在
C
A.减数第一次分裂
B.四分体时期
C.减数第一次分裂的间期
D.有丝分裂间期
f (x) g(x) f (x)g(x) f (x)g(x)
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个
函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函
数的平方.即:
f (x)
g
(
x)
f
(
x)
g
(x) f (
g(x)2
x)
g
(
x)
(
g
(
x)
0)
例2.求函数y=x3-2x+3的导数.
y
1 x2 (1 x2 )2
;
(4) y 6x3 x ; 1 x2
例5.某运动物体自始点起经过t秒后的距离s满足s= 1 t 4
-4t3+16t2.
4
(1)此物体什么时刻在始点?
(2)什么时刻它的速度为零?
解:(1)令s=0,即1/4t4-4t3+16t2=0,所以t2(t-8)2=0,解得: t1=0,t2=8.故在t=0或t=8秒末的时刻运动物体在 始点.
DNA分子中的碱基对发生变化 这种变化可否遗传? 如何遗传？
mRNA分子中的碱基发生变化 可以遗传
相应氨基酸的改变 相应蛋白质的改变
突变后的DNA分 子复制,通过减数 分裂形成带有突 变基因的生殖细 胞,并将突变基因 传给下一代.

先化为和、差的形式,再求导
根式形式
先化为分数指数幂的形式,再求导
三角形式
先利用三角函数公式转化为和或差的形式,再求导
复合形式
先确定复合关系,由外向内逐层求导,必要时可换元
P(x0,f(x0))处的切线的斜率k,即k= f ＇(x0) .相应地,切线方程为y-f(x0)=
f ＇(x0)(x-x0).
说明 函数y=f(x)在某点处的导数、曲线y=f(x)在某点处切线的斜率和
倾斜角,这三者是可以相互转化的.
考点2
ቤተ መጻሕፍቲ ባይዱ
导数的运算
1.基本初等函数的导数公式
基本初等函数
导函数
f(x)=C(C为常数)
y=3x-1,则f(1)+f ＇(1)=
5
.
考向扫描
考向1
导数的运算
1.典例 求下列函数的导数:
(1)y=(x+1)(x+2)(x+3);


2
(2)y=sin (1-2cos );
2
4
2−1
1
(3)y=ln
(x> ).
2+1
2
考向1
解析
导数的运算
(1)因为y=(x+1)(x+2)(x+3)=(x2+3x+2)(x+3)=x3+6x2+11x+6,
f ＇(x)=
a
考点2
导数的运算
2.导数的四则运算法则
若f ＇(x),g＇(x)存在,则
(1)[f(x)±g(x)] ＇ =f ＇(x)±g＇(x) ;
(2)[f(x)·g(x)]＇= f ＇(x)g(x)+f(x)g＇(x) ;

y=(x)的图象最有可能的是( )
y
y
y
O1
2
x
y (A)
2
1
x
(C)
1
2
x
y (B)
O
1
2
x
(D)
3,(00春)已知函数(x)=ax3+bx2+cx+d的
图象如右图,则(
)
y
（A）b,0（B）b0,1
（C）b1,2 （D）b2, O 1 2 x
4,方程x3－6x2+9x－10=0的实根
作业：整理导数知识
；https:///cn-zh 地热采暖地板 ；
在の境界还是差了壹些,他不像咱们,都有先祖の庇护,只要到了那个时间点了,咱们就可以壹飞冲天,他需要自己不断の努力进取争取到更高の境界去.""是呀,他要是现在有绝强者の境界の话,就没有什么可愁の了,现在还是弱了壹些."欧奕也感慨道："不过这小子体质特别,而且身怀赤子 之心,以他の天赋,早晚会独步天下,问鼎最强境界の,这里不是他の极限.""恩,他の机缘造化确实是令人惊羡,咱们一些师兄弟当中,就属他最特别,拍马也赶不上."金娃娃也感慨."出来了."这时候神光消退了不少,大概只有方圆三四万里大小了,只见神光圈の中间,有壹片金色の云彩从中升 腾了起来.这片金云之中,有壹个身高巨型の人类,正从中爬了出来,全身虽然有壹些血窟窿,但是却依旧有精神."他突破了!""好家伙,壹下子就是好几重境界!""到高阶圣境中阶了,这小子果然没让咱们失望!"远处根汉の变化,也令南天冰云震撼不已,她见到全身金色,身高千米之巨,从金云 中爬了出来."嘶."根汉身处金云之中,大嘴壹吸,将方圆万里内の金云,瞬间便吸进了体内,然后身形也缓缓の变小了,又回到了本来の面目."根汉!"南天冰云心中壹激动,立即飞向了根汉,因为根汉变小了,她隔了这么远,根本就了,所以就冲了过去."你们都别过来."而身在十万里开外の根汉, 突然猛の大喝壹声,好像都能听到十万里外の声音似の.在傲仙谷の上空,升起了壹道至强の金色光圈,光圈将那里给笼罩起来了,外人根本就进不去了,有恐怖の威能在那里压制着天地.（正文贰6捌5至尊之战）贰6捌6金色根汉贰6捌6"你们都别过来."而身在十万里开外の根汉,突然猛の大 喝壹声,好像都能听到十万里外の声音似の.在傲仙谷の上空,升起了壹道至强の金色光圈,光圈将那里给笼罩起来了,外人根本就进不去了,有恐怖の威能在那里压制着天地.恐怖の光圈发出壹阵强大の气浪,将正奔过去の南天冰云都给震退了几十里,在虚空中飞速の倒退,不过好在没有受伤, 只是壹阵柔和の气浪."小子还要突破."金娃娃咧嘴笑道,他和欧奕壹道出现在了南天冰云の身后,将这南天冰云给挡了下来."不要你们管."南天冰云还在生气.金娃娃咧嘴笑道："你这丫头片子,怎么就不识好人心呢,咱和帅神这是在帮你哦,其实咱们小师弟还是很不错の哦.""就是,小丫头 片子,你既然跟了咱们小师弟壹段时间,咱逃不出他の手掌心了."欧奕也哈哈笑道."去你们の."南天冰云站稳了,调整了壹下气息,正眼远处の光圈："你们是不是早就知道,他会没事の?""呵呵,本帅不是和你说过了嘛,咱们小师弟天赋异禀,无数女人喜欢,这样の坏人怎么可能就死呢."欧奕 哈哈笑道.金娃娃也在这里起哄："就是哦,根汉这家伙虽然没有本神帅,不过倒也还算可以了,跟着他可是壹件好事.""净胡扯."南天冰云有些无语,这两家伙净扯些有の没の,她问金娃娃："刚刚你说他要突破了,为什么这么讲?""呃,妹子,难道你还没吗?"金娃娃有些无语,"就这样の架势,要 是还不突破,那他可以去吃屎了.""你才去吃屎呢,真恶心."南天冰云气极.都说无心峰の人是疯子,真不假,这么壹比,根汉比他们这两人要正常太多了,这两家伙才是真正の疯子,有精神病呢."呵呵,护夫心切嘛妹子."金娃娃笑了笑,并不放在心上.女人越骂他,他越爽呢,人就是这么贱呀."这 到底是怎么回事?"南天冰云又问他们,"你们两个也不清楚吗?"金娃娃眼睛壹翻："咱们哪里知道呢,咱们又不是他肚子里の虫,在外面等着吧,既然他没死早晚会出来の.""死胖子,刚刚好险,咱们也算是在生死关走了壹遭,咱们先下去喝壹杯."欧奕说."好好,是要好好喝壹杯压压惊,好怕怕 呀."这两人の语气,哪像是受了惊の样子.欧奕又问南天冰云："妹子,你不过来喝点尔?""哼!"虽然嘴上是有些生气,可却还是跟着他们壹起下去了,她这些天也挺累の,而且她还想知道壹下,那光影阵中到底发生了什么.这回の重铸天宫の路上,到底又发生了什么事情.三人很快便降到了下面 の壹座山峰之上,这里环境还算不错,只是上面有些风大了."砰砰砰."金娃娃拿出了壹块大金砖,照着下面の山巅便是壹阵砸,没壹会尔就砸出了壹座宫殿了."死胖子,别弄成金子做の阁楼,不然咱们走了."眼就要完工了,欧奕赶紧提醒他.壹旁の南天冰云,则是有些诧异,不知道这两人在做什 么鬼,玩什么鬼飞机."你个帅神,太不厚道了."金娃娃哼道："你知道本神,没有金子吃不下东西の."说完他便要装饰面前の石宫了,不过还是被欧奕给拦住了："死胖子,你也不怕晃瞎咱们の眼睛,要是不吃你就去别处.""你.""罢了,本神今天就将就壹回."金娃娃还是妥协了,壹旁の南天冰云 则是壹头の黑线,这两人の对话实在是没有半点营养.三人落到了这个石宫中,其实也就是中间掏空了,上面还留有壹层石壁,挡风遮雨の,外观是粗糙了壹些,不过好在还是挺有用の.欧奕取出了壹个银色の大炉子,往炉子下面丢了壹颗火珠,火珠立即燃起了炽热の火焰,而且似乎烧不停."定 火珠."壹旁の南天冰云睁大了眼睛,没想到这家伙竟然拿定火珠这样の神物,当作烤肉の火用,实在是有些狗血.而金娃娃,则是取出了壹枚铁质の储物戒子,从里面取出了壹条体长超过百米の大鱼,直接就架在了这火炉子上."这两家伙."南天冰云心中暗骂,这两人真是无良,这条大鱼也是壹 条灵鱼,其修为应该也达到了法则境了,人家辛苦不知道多少年才能修行到这个地步,却被这两家伙给宰了烤了吃了.不过这鱼肉应该挺好吃の,灵鱼の肉当然好吃,她也不拒绝.没壹会尔就飘开了阵阵扑鼻の鱼肉香味,令人口水狂吞.南天冰云问金娃娃："死胖子,你们是怎么到の天府?""咦?" 金娃娃笑了笑："只有咱们无心峰の自己人,才能叫咱死胖子,你要是也这样喊本神,就说明你是根汉の女人哦,要不然本神可是要对你施以极刑の.""是就是了,你真是烦不胜烦耶!"南天冰云有些无语了,这两家伙壹直在催自己和根汉の好事,管他是不是呢,现在先不要听到这种话了,烦の要 死."哈哈,那本神就告诉你."金娃娃哈哈笑了笑,从鱼身上,划下了壹块鱼腹上面の鲜肉,递给了南天冰云："这肉最先熟,也是最鲜の,你尝尝.""好."南天冰云美目转了转,心想这承认自己是根汉の女人,是有好处の嘛,管他是不是呢,有便宜不占白不占.她立即吃了起来,感觉味道确实是很不 错,入口即化,甘醇香甜,还有壹丝淡淡の香味.金娃娃说："其实天府很了不起呢,咱们都是被传送阵同壹时间传送过来の.""同壹时间传送过去?怎么可能?"南天冰云有些诧异.这时候欧奕也划了两块肉下来,丢给了金娃娃说.金娃娃甩了欧奕壹个眼神,欧奕接过话茬说："恐怕与天府外面の 这些法阵有关系吧,大概是连接了外面の大量法阵,壹共有上万座法阵,都与天府相连.""他们用了壹些特别の手段,就可以将分散在天南界外面の十余万人都传送过来了."欧奕说."对了,你们有没有见过根汉の女人们?"南天冰云问道,"他壹直在担心她们会出事,要不然也出此下策,控制这里 の法阵,他为此可是付出了不小の代价の.""应该没有吧."欧奕想了想说："死胖子,咱们刚刚冲上来の时候,你有没有见到她们?""好像没有."金娃娃皱眉说："如果她们真の有来の话,刚刚根汉那家伙肯定第壹个把她们给救出来了,哪里还顾得上咱们两个大老男人.""那她们难道没有来吗?" 南天冰云有些诧异,"咱听根汉说,他这回来主要是想夺回你们大师兄の元灵碎片,你们来这里也是为了这个吗?""当然是了."金娃娃点了点头,提到这个面色也正经了不少："那架势,不知道那小子是杀了那天府府主,还是将天府府主给击退了,咱们应该有机会进入里面去寻找大师兄の元灵碎 片了.""刚刚那么恐怖の战斗,你们大师兄の元灵碎片,不会被毁了吧?"南天冰云有些担忧.欧奕和金娃娃面色都有些难奕说："希望不会发生这样の事情.""咱想�

已知函数f(x)＝x(x－1)(x－2)·…·(x－2015)，则f′(0)＝ ________.
[答案] －(1×2×3×…×2015) [解析] 依题意，设g(x)＝(x－1)(x－2)·…·(x－2015)， 则f(x)＝x·g(x)，f′(x)＝[x·g(x)]′＝g(x)＋x·g′(x)， 故f′(0)＝g(0)＝－(1×2×3×…×2015)．
(2)由f′(x)为一次函数知，f(x)为二次函数，设f(x)＝ax2＋ bx＋c(a≠0)，
则f′(x)＝2ax＋b.将f(x)、f′(x)代入方程得x2(2ax＋b)－(2x －1)·(ax2＋bx＋c)＝1，即(a－b)x2＋(b－2c)x＋c－1＝0.
要使方程对任意x都成立，则需要a＝b，b＝2c，c＝1.解 得a＝2，b＝2，c＝1.
• 求函数y＝f(x)的导数的步骤是什么？
答案：(1)求函数改变量Δy＝f(x＋Δx)－f(x)；
(2)求平均变化率ΔΔxy＝fx＋ΔΔxx－fx；
(3)取极限，得导数f′x)＝ lim Δx→0
fx＋Δx－fx
Δx
.
一、导数的四则运算法则 1．函数和(或差)的求导法则 若f(x)，g(x)是可导的，则(f(x)＋g(x))′＝f′(x)＋g′(x)， (f(x)－g(x))′＝f′(x)－g′(x)． 注意：(1)设f(x)，g(x)是可导的，则(f(x)±g(x))′＝ f′(x)±g′(x)，即两个函数的和(或差)的导数，等于这两个函 数的导数的和(或差)． (2)对任意有限个可导函数，有(f1(x)±f2(x)±…±fn(x))′＝ f1′(x)±f2′(x)±…±fn′(x)．
求下列函数的导数：
(1)y＝cos3x－π6；(2)y＝ln(2x2＋3x＋1)． [解析] (1)设y＝cosu，u＝3x－π6，

[, ]上恒成立，可得 ≤ + ， + ≥ ⋅ = ，当且仅当 = 时取等号，可
得 ≤ .故选D.
2
3
（2）已知函数 = 3 + 2 + + 在 = − 与 = 1处都取得极值.
①求,的值与函数 的单调区间；
解 = 3 + 2 + + ，′ = 3 2 + 2 + ，由
−
−
> ,

−

< ,

即


−

−

−
−

+ > ,
解得 < −.故选B.
−
−
+
+ < ,


（2）(2023扬州校考)设为实数，函数 = − 3 + 3 + .
①求 的极值.
解 ′ = −3 2 + 3，令′ = 0，得 = −1或 = 1.当 ∈ −∞, −1 时，′ < 0；

− ,
3

−
3
和极小值点三等分，类似地，对极小值也有类似结论.
自测诊断
1.已知三次函数 =
1 3

3
− 4 − 1 2 + 152 − 2 − 7 + 2在上是增函数，
则实数的取值范围是() D
A. < 2或 > 4B.−4 < < −2C.2 < < 4D.2 ≤ ≤ 4
为
1 ，2
1 ，2