导数与三次函数的关系

第28关：三次函数专题—全解全析一、定义：定义1、形如的函数，称为“三次函数”（从函数解析式的结构上命名）定义2、三次函数的导数，把叫做三次函数导函数的判别式二、三次函数图象与性质的探究：1、单调性一般地，当时，三次函数在上是单调函数；当时，三次函数在上有三个单调区间（根据两种不同情况进行分类讨论）2、对称中心三次函数是关于点对称，且对称中心为点，此点的横坐标是其导函数极值点的横坐标。

证明：设函数的对称中心为（m，n）。

按向量将函数的图象平移，则所得函数是奇函数，所以化简得：上式对恒成立，故，得，。

所以，函数的对称中心是（）。

可见，y＝f(x)图象的对称中心在导函数y＝的对称轴上，且又是两个极值点的中点，同时也是二阶导为零的点。

3、三次方程根的问题（1）当△=时，由于不等式恒成立，函数是单调递增的，所以原方程仅有一个实根。

（2）当△=时，由于方程有两个不同的实根，不妨设，可知，为函数的极大值点，为极小值点，且函数在和上单调递增，在上单调递减。

此时：①若，即函数极大值点和极小值点在轴同侧，图象均与轴只有一个交点，所以原方程有且只有一个实根。

②若，即函数极大值点与极小值点在轴异侧，图象与轴必有三个交点，所以原方程有三个不等实根。

③若，即与中有且只有一个值为0，所以，原方程有三个实根，其中两个相等。

4、极值点问题若函数f(x)在点x0的附近恒有f(x)≥f(x) (或f(x)≤f(x))，则称函数f(x)在点x0处取得极大值（或极小值），称点x为极大值点（或极小值点）。

当时，三次函数在上的极值点要么有两个。

当时，三次函数在上不存在极值点。

5、最值问题函数若，且，则：；三、三次函数与导数专题：1. 三次函数与导数例题例1. 函数.（1）讨论函数的单调性；（2）若函数在区间（1，2）是增函数，求的取值范围.解：（Ⅰ），的判别式△=36（1-a）.（ⅰ）当a≥1时，△≤0，则恒成立，且当且仅当，故此时在R上是增函数.来自QQ群3（ⅱ）当且，时，有两个根：，若，则, 当或时，，故在上是增函数；当时，，故在上是减函数；若，则当或时，，故在和上是减函数；当时，，故在上是增函数；（Ⅱ）当且时,,所以当时，在区间（1，2）是增函数.当时，在区间（1,2）是增函数，当且仅当且，解得.综上，的取值范围是.例 2. 设函数，其中。

4导数研究三次函数的性质复习目标：掌握三次函数的图象和性质，尤其是利用导数研究单调性、极值情况，以及三次函数的零点。

复习重点难点：（1）三次函数的图象的四种情况；（2）三次函数的极值情况；【典型例题】题型一：三次函数单调性的讨论例1．已知函数32()2f x ax x x =++在R 上恒为增函数，求实数a 的取值范围.例2．已知函数f (x )=-x 3＋3x 2＋9x ＋a ,（I ）求f (x )的单调递减区间；（II ）若f (x )在区间[－2，2]上的最大值为20，求它在该区间上的最小值．题型二：三次函数极值，最值的讨论例3. 已知a 是实数，函数2()()f x x x a =-；（1）若'(1)3f =，求a 的值及曲线()y f x =在点(1,(1))f 处的切线方程；（2）求()f x 在区间[]2,0上的最大值．例4．已知函数()f x 的导数2()33,f x x ax '=-(0).f b =,a b 为实数，12a <<.（1）若()f x 在区间[1, 1]-上的最小值、最大值分别为2-、1，求a 、b 的值；（2）设函数2()(()61)x F x f x x e '=++⋅，试判断函数()F x 的极值点个数．【课后作业】1.过曲线y ＝x 3+x-2上的点P 0的切线平行于直线y ＝4x-1,则切点P 0的坐标为2．已知向量a ＝(x 2，x ＋1)，b ＝(1－x ，t )．若函数f (x )＝a·b 在区间(－1,1)上是增函数，求t 的取值范围．3．函数f (x )=x 3＋x 2－x 在区间［－2，1］上的最大值和最小值分别是4.已知某生产厂家的年利润y （单位：万元）与年产量x （单位：万件）的函数关系式为31812343y x x =-+-，则使该生产厂家获得最大年利润的年产量为5．设函数b x a ax x x f +-+-=2233231)( (0<a <1)． (1)求函数)(x f 的单调区间； (2)当x ∈[]2,1++a a 时，不等式|()x f/ |≤a ，求a 的取值范围．6.已知函数3221()21(0)32a f x x x a x a =--+> （1）求函数()f x 的极值；（2）若函数()y f x =的图象与值线0y =恰有三个交点，求实数a 的取值范围；（3）已知不等式2'()1f x x x <-+对任意(1,)a ∈+∞都成立，求实数x 的取值范围.7.已知函数()()a x x f -=2()x b -,b a ,为常数,(1)若a b ≠,求证:函数()x f 存在极大值和极小值(2)设()x f 取得极大值、极小值时自变量分别为12,x x ,令点A 11(,()x f x ),B 22(,()x f x ),若a >b ，直线AB 的斜率为12-,求函数()x f 和/()f x 的公共递减区间的长度.答案：【典型例题】1． 61≥a . 2．（I ） 0)(,963)(2<'++-='x f x x x f 令，解得x <－1或x >3所以函数f (x )的单调递减区间为（－∞，－1），（3，＋∞）．（II ）)}2(),2(max{)(,5)1()(,3212m ax m in f f x f a f x f -=+-=-=∴<<-<-)2()2(,22)2(,2)2(->∴+=+=-f f a f a f 于是有 22＋a ＝20，解得 a ＝－2．故f (x )=－x 3＋3x 2＋9x －2，因此f (－1)＝－7，即函数f (x )在区间[－2，2]上的最小值为－7．3. 解析：（1）2'()32f x x ax =-．因为'(1)323f a =-=，所以0a =．又当0a =时，(1)1,'(1)3f f ==，所以曲线()(1,(1))y f x f =在处的切线方程为3x y --2=0．（2）令'()0f x =，解得1220,3a x x ==． 当203a ≤，即a ≤0时，()f x 在[0，2]上单调递增，从而max (2)84f f a ==-． 当223a ≥时，即a ≥3时，()f x 在[0，2]上单调递减，从而max (0)0f f ==． 当2023a <<，即03a <<，()f x 在20,3a ⎡⎤⎢⎥⎣⎦上单调递减，在2,23a ⎡⎤⎢⎥⎣⎦上单调递增，从而max 84,0 2.0,2 3.a a f a -<≤⎧⎪=⎨<<⎪⎩综上所述，max 84, 2.0, 2.a a f a -≤⎧⎪=⎨>⎪⎩4.解（Ⅰ）由已知得，323()2f x x ax b =-+； 由()0f x '=，得10x =，2x a =． ∵[1, 1]x ∈-，12a <<，∴ 当[1, 0)x ∈-时，()0f x '>，()f x 递增；当(0, 1]x ∈时，()0f x '<，()f x 递减．∴ ()f x 在区间[1, 1]-上的最大值为(0)f b =，∴1b =． 又33(1)11222f a a =-+=-，33(1)1122f a a -=--+=-，∴ (1)(1)f f -<． 由题意得(1)2f -=-，即322a -=-，得43a =．故43a =，1b =为所求． （Ⅱ） 2222()(3361)33(2)1x x F x x ax x e x a x e ⎡⎤=-++⋅=--+⋅⎣⎦． ∴ []222()63(2)233(2)1x x F x x a e x a x e '⎡⎤=--⋅+--+⋅⎣⎦22[66(3)83]x x a x a e =--+-⋅．二次函数266(3)83y x a x a =--+-的判别式为22236(3)24(83)12(31211)123(2)1a a a a a ⎡⎤∆=---=-+=--⎣⎦，令0∆≤，得：21(2),22333a a -≤-≤≤+令0∆>，得2,233a a <->+或 ∵20x e >，12a <<，∴当22a ≤<时，()0F x '≥，函数()F x 为单调递增，极值点个数为0；当12a <<()0F x '=有两个不相等的实数根，根据极值点的定义，可知函数()F x 有两个极值点．【课后作业】1.(1,0)或(-1,-4)2.解：f (x )＝a·b ＝x 2(1－x )＋t (x ＋1)＝－x 3＋x 2＋tx ＋t ，……4分∴f ′(x )＝－3x 2＋2x ＋t . …………7分∵f (x )在(－1,1)上是增函数，∴－3x 2＋2x ＋t ≥0在x ∈(－1,1)上恒成立．∴t ≥3x 2－2x ， ……………11分令g (x )＝3x 2－2x ，x ∈(－1,1)．∴g (x )∈⎣⎡⎭⎫－13，5，∴t ≥5. ……………15分3． f (x )max =1,f (x )min =－2。

导数在三次函数中的应用
欢迎来到三次函数与导数的世界！
首先，让我们来探讨一下什么是三次函数。

三次函数是一种把一个变量x关于另一个变量y的函数，其具体形式为：y=ax^3+bx^2+cx+d，其中a、b、c、d为实数，a不等于0。

大部分三次函数可以给出一个三次曲线，比如抛物线、弓形线等。

其次，让我们来讨论它的导数的概念。

在数学中，导数是表示函数变化率的量，也是函数的增量与x轴距离之比，也就是函数的斜率。

在三次函数中，它的一阶导数为：
y'=3ax^2+2bx+c；2阶导数为：y''=6ax+2b；3阶导数为：y'''=6a。

最后，让我们来讨论三次函数和导数在应用中的作用。

三次函数可以用来表示许多实际应用中的几何和物理运动,比如抛物线在射击中的运动，弓形线在心脏收缩的过程中的运动等。

三次函数的导数可以应用到各种数学和物理问题上，例如求一阶和二阶导数，可以用它来求抛物线的加速度、弓形线的加速度等等。

此外，可以用它来求解一些复杂的数学问题，比如求函数的极值，微分方程的积分等。

总而言之，三次函数和导数有着多功能的应用，它们可以用来解决许多数学和物理问题，并且有助于我们解决复杂的问题。

数学中的三次函数和导数是一个很重要的概念，并且可以应用到几乎任何物理问题之上。

专题：用导数研究三次函数的性质★★★教学目标1、 掌握三次函数的定义和解析式；2、 掌握用导数求三次函数的切线方程、单调区间、极值和最值；3、 能利用三次函数的图象和性质解决与三次函数有关的问题．知识梳理1．三次函数的定义：形如 的函数叫做三次函数． 2．三次函数的几种表达式：（1）一般形式： ；（2）已知函数的对称中心为),(n m ，则()f x = ；（3）已知函数图象与x 轴三个交点的横坐标)(,,γ<β<αγβα，则()f x = ； （4）已知函数图象与x 轴的一个交点的横坐标0x ，则()f x = ． 3．三次函数)0()(23>+++=a d cx bx ax x f 的性质：2()32(0)f x ax bx c a '=++>，则2()320f x ax bx c '=++=的判别式222124(4)b ac b ac =-=-△()．（1）函数的定义域为 ，值域为 ；（2）单调性：①若22120b ac =-≤△()，此时函数()f x 在上 是增函数；②若22120b ac =->△()，令2()320f x ax bx c '=++=两根为12,x x 且12x x <，则()f x 在上 单调递增，在 上单调递减；（3）极值：①若 ，此时函数无极值；②若0△>，且2()320f x ax bx c '=++=两根为12,x x 且12x x <，此时函数()f x 在 处取极大值 ，在 处取极小值 ． 答案：１．)0(23≠+++=a d cx bx ax y ．2．（1）32()(0)f x ax bx cx d a =+++≠；（2）3()()(0)A x m B x m n a -+-+≠；（3）()()()(0)a x x x a αβγ---≠；（4）20()()(0)x x ax mx n a -++≠．3．（1）R ， R ；（2）①R ；②12(,),()x x -∞+∞，12(,)x x ；（3）①0≤△，②1x x =，)(1x f ，2x x =，)(2x f ．思维升华：1． 三次函数d cx bx ax x f +++=23)(当且仅当 时是奇函数？2． 三次函数d cx bx ax x f +++=23)(的图象是对称图形吗？如果是，那么对称中心或对称轴是什么？ 答案：1． 0==d b ．2．图象关于点))3(,3(abf a b --中心对称． 证明如下：三次函数d cx bx ax x f +++=23)(关于点（m ，n ）对称的充要条件是n x m f x m f 2)()(=++-，即])()()([23d x m c x m b x m a +-+-+-+32[()()a m x b m x +++ ()]2c m x d n +++=，整理得，n d mc bm am x b ma 2)2222()26(232=+++++，据多项式恒等对应系数相等，可得a b m 3-=且d mc bm am n +++=23=)3()(abf m f -=，从而三次函数是中心对称曲线，且对称中心是))3(,3(abf a b --． 典例精讲30 min.例1（★★★）（全国卷2文）已知函数f （x ）=x 3-3ax 2+3x+1． （Ⅰ）设a=2，求f （x ）的单调期间；（Ⅱ）设f （x ）在区间（2，3）中至少有一个极值点，求的取值范围．分析：（1）求出函数的导数，由导数大于0，可求得增区间，由导数小于0，可求得减区间．（2）求出函数的导数'()f x ，在（2，3）内有极值，即为'()f x 在（2，3）内有一个零点，即可根据'(2)'(3)0f f <，即可求a 出的取值范围．解：当2a =时，32()631f x x x x =-++，'()3(23)(23)f x x x =--，当(,23)x ∈-∞时，'()0f x >，()f x 在(,23)-∞单调增加； 当(23,23)x ∈时，'()0f x <，()f x 在(23,23)单调减少； 当(23,)x ∈+∞时，'()0f x >，()f x 在(23,)+∞单调增加．综上所述，()f x 的单调增区间是(,23)(23,)-∞+∞和．()f x 的单调减区间是(23,23)．（II ））22'()3[()1]f x x a a =-+-．当210a -≥时， '()0f x >，()f x 为增函数，故()f x 无极值点；当210a -<时，'()0f x =有两个根12x a x a ==+由题意知，23a << ①或23a < ② ①式无解，②式的解为5543a <<， 因此a 的取值范围是5543⎛⎫ ⎪⎝⎭，． 点评：三次函数的单调性判定与一般函数一样，利用函数的导数来求解，求极值时，要注意函数取得极值时的充要条件． 巩固练习（★★★）已知函数f (x )=-x 3＋3x 2＋9x ＋a ， （I ）求f (x )的单调递减区间；（II ）若f (x )在区间[－2，2]上的最大值为20，求它在该区间上的最小值． 解析：（I ） 0)(,963)(2<'++-='x f x x x f 令，解得x <－1或x >3 所以函数f (x )的单调递减区间为（－∞，－1），（3，＋∞）． （II ）)}2(),2(max{)(,5)1()(,3212m ax m in f f x f a f x f -=+-=-=∴<<-<-(2)2,(2)22,(2)(2)f a f a f f -=+=+∴>-，于是有 22＋a ＝20，解得 a ＝－2．故f (x )=－x 3＋3x 2＋9x －2，因此f (－1)＝－7， 即函数f (x )在区间[－2，2]上的最小值为－7．例2（★★★）已知函数f （x ）=3231()2ax x x R -+∈，其中a>0． （Ⅰ）若a=1，求曲线y=f （x ）在点（2，f （2））处的切线方程； （Ⅱ）若在区间11,22⎡⎤-⎢⎥⎣⎦上，f （x ）>0恒成立，求a 的取值范围． 分析：先求切点坐标，再利用导数求出切线斜率，可得切线方程；再利用三次函数的图象求解函数的极值来解不等式．解：（Ⅰ）当a=1时，f （x ）=323x x 12-+，f （2）=3；'()f x =233x x -， '(2)f =6．所以曲线y=f （x ）在点（2，f （2））处的切线方程为y-3=6（x-2），即y=6x-9．（Ⅱ）'()f x =2333(1)ax x x ax -=-．令'()f x =0，解得x=0或x=1a．以下分两种情况讨论： （1） 若110a 2<≤≥，则，当x 变化时，'()f x ，f （x ）的变化情况如下表： 当11x f x 22⎡⎤∈-⎢⎥⎣⎦，时，（）>0等价于5a 10,()0,8215a ()0,0.28f f -⎧⎧>->⎪⎪⎪⎪⎨⎨+⎪⎪>>⎪⎪⎩⎩即 解不等式组得-5<a<5．因此0a 2<≤．（2） 若a>2，则11<<．当x 变化时，'()f x ，f （x ）的变化情况如下表：当11x 22⎡⎤∈-⎢⎥⎣⎦，时，f （x ）>0等价于1f(-)21f()>0,a ⎧⎪⎪⎨⎪⎪⎩>0,即25811->0.2a a -⎧⎪⎪⎨⎪⎪⎩>0,解不等式组得52a <<或2a <-．因此2<a<5． 综合（1）和（2），可知a 的取值范围为0<a<5．点评：三次函数的切线问题，要看清问题是在某点处的切线，还是过某点的切线，确定切线的切点是关键点．利用函数的图象来求解不等式也是常用之法． 巩固练习（★★★）已知函数xxxxf3231)(23+-=（Rx∈）的图象为曲线C．（1）求过曲线C上任意一点的切线的倾斜角的取值范围；（2）若在曲线C上存在两条相互垂直的切线，求其中一条切线与曲线C的切点的横坐标的取值范围；解析：（1）34)(2+-='xxxf，则11)2()(2-≥--='xxf，即过曲线C上任意一点的切线斜率的取值范围是[)+∞-,1；故倾斜角取值范围为3[0,)[,)24πππ⋃．（2）由（1）可知，⎪⎩⎪⎨⎧-≥--≥111kk解得01<≤-k或1≥k，由03412<+-≤-xx或1342≥+-xx．得：(][)+∞+-∞-∈,22)3,1(22,x；例3（★★★）设Ra∈，讨论关于x的方程0323=-+axx的相异实根的个数？分析：讨论三次方程的根的问题，可化为讨论三次函数的极值点与x轴之间的关系问题．解：0,263)()(212=-==+='xxxxxfxf的两根为导函数函数，，fxffxf0)0()(,4)2()(==-∴的极小值是的极大值是函数如图所示，（1）当0<a或4>a时，函数)(xf与)(xg只有一个交点，即方程只有一个根．（2）当0=a或4=a时，函数)(xf与)(xg只有两个交点，即方程只有两个根．（3）当40<<a时，函数)(xf与)(xg有三个交点，方程有三个根．点评：讨论三次函数的极值的大小与0的关系，可以解决三次方程根的个数问题．可以总结如下的经验：从数形结合的视角看三次方程320(0)ax bx cx d a+++=>的实数根：（1）若22120b ac =-≤△()，方程有且只有一个实数解；（2）若22120b ac =->△()，令2()320f x ax bx c '=++=两根为12,x x 且12x x <， ①若0)()(21<⋅x f x f ，则方程有三个不同的实数解)(,,γ<β<αγβα，且有γ<<β<<α21x x ，②若0)(0)(21==x f x f 或，则方程有两个不同的实数解，③若0)()(21>⋅x f x f ，则方程有且只有一个实数解α，且21x x >α<α或， 巩固练习（★★★）若函数()33f x x x a =-+有3个不同的零点，则实数a 的取值范围是 ．答案：()2,2- 解析：2'()33f x x =-，则'()0f x =可得1x =±，则有(1)0(1)0f f <⎧⎨->⎩，可解得22x -<<．回顾总结4 min.1．容易忽视三次函数的切线的特殊性而出错．例如3()2f x x x =-+经过(1,2)P 有几条切线？常见的错解有：把P 点当做切点，判定经过P 点只有一条，而实际上要分是否为切点两种情况来看． 2．容易忽视三次函数的图象的特殊性而出错．例如在讨论三次方程有三个根的问题时，不知道函数的极大值大于0且函数的极小值小于0．典型错题反思反思是自觉地对数学认知活动进行分析、总结、评价和调控的过程，是一种自我挑战、自我完善和自我超越，是优化解法、深化思维的有效手段，是高效的学习方法、最佳的纠错手段，是走出“题海”的最有效途径．请整理出本课时的典型错误，找出错因，并从审题、知识、方法和策略的层面进行反思！ 我的错题：错因：反思：。

三次函数的导数与导函数引言三次函数是指次数为3的多项式函数，其一般形式为 f(x) =ax^3 + bx^2 + cx + d。

在本文中，将讨论三次函数的导数与导函数。

导数的定义导数是函数在某一点处的变化率。

对于三次函数 f(x) = ax^3 +bx^2 + cx + d，其导数可以通过求函数的微分得到。

微分就是对函数进行局部线性近似，即求切线的斜率。

三次函数的导数计算根据导数的定义，可以使用微分的方法求出三次函数的导数。

首先，对三次函数 f(x) 进行微分得到 f'(x)。

然后求导数的公式为f'(x) = 3ax^2 + 2bx + c。

导函数的意义导函数是三次函数的导数，它描述了函数在不同点的变化率。

导函数的图像可以反映出原函数的整体趋势。

导函数的图像特点根据导函数的公式 f'(x) = 3ax^2 + 2bx + c，可以得到以下结论：- 如果 a>0，那么导函数是向上开口的抛物线；- 如果 a<0，那么导函数是向下开口的抛物线；- b 的值决定了导函数的平移与压缩；- c 的值决定了导函数的上下偏移。

导函数与原函数的关系根据导函数与原函数的关系，可以推导出以下结论：- 如果三次函数 f(x) 在某一点处的导数为0，那么该点是函数的极值点；- 如果三次函数 f(x) 的导函数恒为正，那么原函数是递增的；- 如果三次函数 f(x) 的导函数恒为负，那么原函数是递减的。

结论本文介绍了三次函数的导数与导函数的概念，并讨论了它们的计算方法、图像特点以及与原函数的关系。

对于进一步理解三次函数及其特性具有一定的参考价值。

> 注意：本文所述内容仅为概念介绍，具体应用时请结合实际情况进行分析和计算。

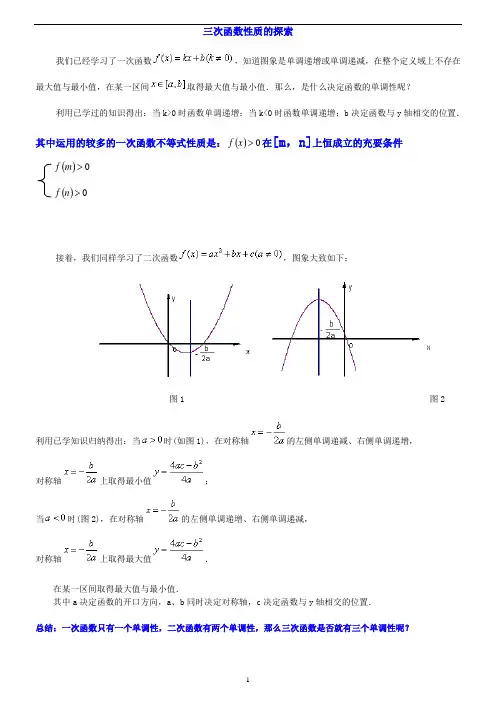
三次函数性质的探索我们已经学习了一次函数，知道图象是单调递增或单调递减，在整个定义域上不存在最大值与最小值，在某一区间取得最大值与最小值．那么，是什么决定函数的单调性呢？利用已学过的知识得出：当k>0时函数单调递增；当k<0时函数单调递增；b决定函数与y轴相交的位置．其中运用的较多的一次函数不等式性质是：()0>f在[m，n]上恒成立的充要条件x()0>fm()0>fn接着，我们同样学习了二次函数，图象大致如下：图1 图2利用已学知识归纳得出：当时(如图1)，在对称轴的左侧单调递减、右侧单调递增，对称轴上取得最小值；当时(图2)，在对称轴的左侧单调递增、右侧单调递减，对称轴上取得最大值．在某一区间取得最大值与最小值．其中a决定函数的开口方向，a、b同时决定对称轴，c决定函数与y轴相交的位置．总结：一次函数只有一个单调性，二次函数有两个单调性，那么三次函数是否就有三个单调性呢？三次函数专题一、定义：定义1、形如32(0)y ax bx cx d a =+++≠的函数，称为“三次函数”（从函数解析式的结构上命名）。

定义2、三次函数的导数232(0)y ax bx c a '=++≠，把2412b ac ∆=-叫做三次函数导函数的判别式。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题，已经成为高考命题的一个新的热点和亮点。

特别是文科。

系列探究1：从最简单的三次函数3x y =开始反思1：三次函数31y x =+的相关性质呢？ 反思2：三次函数31y x =-+的相关性质呢？ 反思3：三次函数()311y x =-+的相关性质呢？（2012天津理）（4）函数22)(3-+=x x f x在区间(0,1)内的零点个数是 B （A ）0 （B ）1 （C ）2 （D ）3系列探究2：探究一般三次函数)0()(23>+++=a d cx bx ax x f 的性质：先求导2()32(0)f x ax bx c a '=++>1．单调性：（1）若22120b ac =-≤△()，此时函数()f x 在R 上是增函数；（2）若22120b ac =->△()，令2()320f x ax bx c '=++=两根为12,x x 且12x x <，则()f x 在12(,),()x x -∞+∞上单调递增，在12(,)x x 上单调递减。