导数与三次函数的关系(1)

第28关：三次函数专题—全解全析一、定义：定义1、形如的函数，称为“三次函数”（从函数解析式的结构上命名）定义2、三次函数的导数，把叫做三次函数导函数的判别式二、三次函数图象与性质的探究：1、单调性一般地，当时，三次函数在上是单调函数；当时，三次函数在上有三个单调区间（根据两种不同情况进行分类讨论）2、对称中心三次函数是关于点对称，且对称中心为点，此点的横坐标是其导函数极值点的横坐标。

证明：设函数的对称中心为（m，n）。

按向量将函数的图象平移，则所得函数是奇函数，所以化简得：上式对恒成立，故，得，。

所以，函数的对称中心是（）。

可见，y＝f(x)图象的对称中心在导函数y＝的对称轴上，且又是两个极值点的中点，同时也是二阶导为零的点。

3、三次方程根的问题（1）当△=时，由于不等式恒成立，函数是单调递增的，所以原方程仅有一个实根。

（2）当△=时，由于方程有两个不同的实根，不妨设，可知，为函数的极大值点，为极小值点，且函数在和上单调递增，在上单调递减。

此时：①若，即函数极大值点和极小值点在轴同侧，图象均与轴只有一个交点，所以原方程有且只有一个实根。

②若，即函数极大值点与极小值点在轴异侧，图象与轴必有三个交点，所以原方程有三个不等实根。

③若，即与中有且只有一个值为0，所以，原方程有三个实根，其中两个相等。

4、极值点问题若函数f(x)在点x0的附近恒有f(x)≥f(x) (或f(x)≤f(x))，则称函数f(x)在点x0处取得极大值（或极小值），称点x为极大值点（或极小值点）。

当时，三次函数在上的极值点要么有两个。

当时，三次函数在上不存在极值点。

5、最值问题函数若，且，则：；三、三次函数与导数专题：1. 三次函数与导数例题例1. 函数.（1）讨论函数的单调性；（2）若函数在区间（1，2）是增函数，求的取值范围.解：（Ⅰ），的判别式△=36（1-a）.（ⅰ）当a≥1时，△≤0，则恒成立，且当且仅当，故此时在R上是增函数.来自QQ群3（ⅱ）当且，时，有两个根：，若，则, 当或时，，故在上是增函数；当时，，故在上是减函数；若，则当或时，，故在和上是减函数；当时，，故在上是增函数；（Ⅱ）当且时,,所以当时，在区间（1，2）是增函数.当时，在区间（1,2）是增函数，当且仅当且，解得.综上，的取值范围是.例 2. 设函数，其中。

三次函数的导数与导函数引言三次函数是指次数为3的多项式函数，其一般形式为 f(x) =ax^3 + bx^2 + cx + d。

在本文中，将讨论三次函数的导数与导函数。

导数的定义导数是函数在某一点处的变化率。

对于三次函数 f(x) = ax^3 +bx^2 + cx + d，其导数可以通过求函数的微分得到。

微分就是对函数进行局部线性近似，即求切线的斜率。

三次函数的导数计算根据导数的定义，可以使用微分的方法求出三次函数的导数。

首先，对三次函数 f(x) 进行微分得到 f'(x)。

然后求导数的公式为f'(x) = 3ax^2 + 2bx + c。

导函数的意义导函数是三次函数的导数，它描述了函数在不同点的变化率。

导函数的图像可以反映出原函数的整体趋势。

导函数的图像特点根据导函数的公式 f'(x) = 3ax^2 + 2bx + c，可以得到以下结论：- 如果 a>0，那么导函数是向上开口的抛物线；- 如果 a<0，那么导函数是向下开口的抛物线；- b 的值决定了导函数的平移与压缩；- c 的值决定了导函数的上下偏移。

导函数与原函数的关系根据导函数与原函数的关系，可以推导出以下结论：- 如果三次函数 f(x) 在某一点处的导数为0，那么该点是函数的极值点；- 如果三次函数 f(x) 的导函数恒为正，那么原函数是递增的；- 如果三次函数 f(x) 的导函数恒为负，那么原函数是递减的。

结论本文介绍了三次函数的导数与导函数的概念，并讨论了它们的计算方法、图像特点以及与原函数的关系。

对于进一步理解三次函数及其特性具有一定的参考价值。

> 注意：本文所述内容仅为概念介绍，具体应用时请结合实际情况进行分析和计算。

专题2-2三次函数图像与性质【题型1】求三次函数的解析式【题型2】三次函数的单调性问题【题型3】三次函数的图像【题型4】三次函数的最值、极值问题【题型5】三次函数的零点问题【题型6】三次函数图像，单调性，极值，最值综合问题【题型7】三次函数对称中心【题型8】三次函数的切线问题【题型9】三次函数根与系数的关系1/342/34【题型1】求三次函数的解析式（1）一般式：()³²f x ax bx cx d =+++（a ≠0）（2）交点式：()123()()()f x a x x x x x x =---（a ≠0）1．若三次函数()f x 满足()()()()00,11,03,19f f f f ''====，则()3f =（）A ．38B ．171C ．460D ．965【解析】待定系数法，求函数解析式设()³²f x ax bx cx d =+++，则()232f x ax bx c '=++，由题意可得：()()()()0011031329f d f a b c d f c f a b c ⎧==⎪=+++=⎪⎨==⎪⎪=+'=⎩'+，解得101230a b c d =⎧⎪=-⎪⎨=⎪⎪=⎩，则()3210123f x x x x =-+，所以()32310312333171f =⨯-⨯+⨯=.【题型2】三次函数的单调性问题三次函数是高中数学中的一个重要内容，其考点广泛且深入，主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。

以下是对三次函数常见考点的详细分析：1.三次函数的定义与形式∙定义：形如f (x )=ax 3+bx 2+cx +d （其中a ≠=0）的函数称为三次函数。

∙形式：注意系数a ,b ,c ,d 的作用，特别是a 的正负决定了函数的开口方向（a >0开口向上，a <0开口向下）。

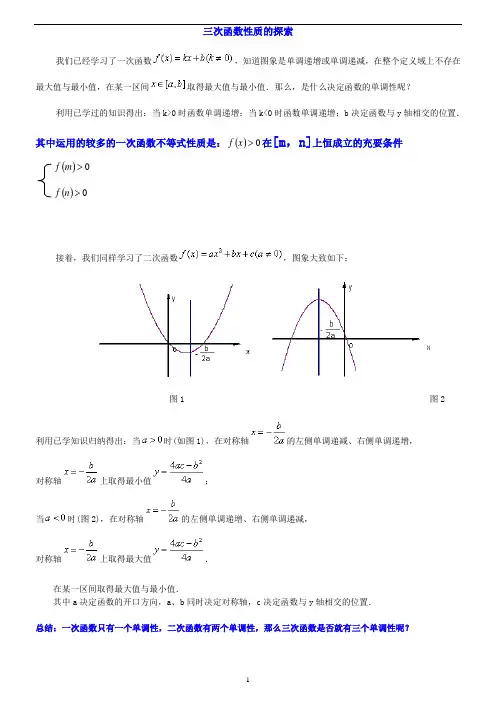
三次函数性质的探索我们已经学习了一次函数，知道图象是单调递增或单调递减，在整个定义域上不存在最大值与最小值，在某一区间取得最大值与最小值．那么，是什么决定函数的单调性呢？利用已学过的知识得出：当k>0时函数单调递增；当k<0时函数单调递增；b决定函数与y轴相交的位置．其中运用的较多的一次函数不等式性质是：()0>f在[m，n]上恒成立的充要条件x()0>fm()0>fn接着，我们同样学习了二次函数，图象大致如下：图1 图2利用已学知识归纳得出：当时(如图1)，在对称轴的左侧单调递减、右侧单调递增，对称轴上取得最小值；当时(图2)，在对称轴的左侧单调递增、右侧单调递减，对称轴上取得最大值．在某一区间取得最大值与最小值．其中a决定函数的开口方向，a、b同时决定对称轴，c决定函数与y轴相交的位置．总结：一次函数只有一个单调性，二次函数有两个单调性，那么三次函数是否就有三个单调性呢？三次函数专题一、定义：定义1、形如32(0)y ax bx cx d a =+++≠的函数，称为“三次函数”（从函数解析式的结构上命名）。

定义2、三次函数的导数232(0)y ax bx c a '=++≠，把2412b ac ∆=-叫做三次函数导函数的判别式。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题，已经成为高考命题的一个新的热点和亮点。

特别是文科。

系列探究1：从最简单的三次函数3x y =开始反思1：三次函数31y x =+的相关性质呢？ 反思2：三次函数31y x =-+的相关性质呢？ 反思3：三次函数()311y x =-+的相关性质呢？（2012天津理）（4）函数22)(3-+=x x f x在区间(0,1)内的零点个数是 B （A ）0 （B ）1 （C ）2 （D ）3系列探究2：探究一般三次函数)0()(23>+++=a d cx bx ax x f 的性质：先求导2()32(0)f x ax bx c a '=++>1．单调性：（1）若22120b ac =-≤△()，此时函数()f x 在R 上是增函数；（2）若22120b ac =->△()，令2()320f x ax bx c '=++=两根为12,x x 且12x x <，则()f x 在12(,),()x x -∞+∞上单调递增，在12(,)x x 上单调递减。

三次函数的图像与性质形如f（x）=ax3+bx2+cx+d（a≠0）的函数叫做三次函数。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题已经成为高考命题的一个新的热点和亮点，尤其是文科数学更是如此。

我们可以采用类比的方法，利用几何画板，较为深入地研究三次函数的图像与性质以及三次方程的解的个数的问题。

１三次函数的图像与性质设三次函数f（x）=ax3+bx2+cx+d（a≠0），其导函数f’（x）=3ax2+2bx+c，其判别式△=4b2-12ac=4（b2-3ac）。

当a>0时，若△>0，方程f’（x）=0有两个不相等的实数根，记作x1，x2，不妨令x1f（x2）。

结论1：f（x1）·f（x2）>0时，函数f（x）的图像与x轴有且仅有一个公共点；f（x1）·f（x2）=0时，函数f（x）的图像与x轴有且仅有两个公共点；f （x1）·f（x2）０，f（x2）0为例）：当a>0时，f（x）的四种图象３推论设三次函数f（x）＝ax3+bx2+cx+d（a>0），其导函数f’（x）=3ax2+2bx+c 的判别式△=4b2-12ac=4（b2-3ac）>0。

方程f’（x）=0有两个不相等的实数根，记作x1，x2，不妨令x1<x2，则函数f（x）在x=x1处取得极大值f（x1），函数f（x）在x=x2处取得极小值f（x2）。

类似可知a<0的情形（其余条件同前）：函数在x=x1处取得极小值f（x1），函数f（x）在x=x2处取得极大值f（x2）。

４例题例1.（湖南卷）用长为18 cm的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？解：设长方体的宽为x（m），则长为2x（m），高为h==4.5-3x（m）（0<x<），故长方体的体积为V（x）=2x2（4.5-3x）＝９x2－６x３（m３）（0<x<），从而V’（x）=18x-18x2（4.5-3x）=18x（１－x）。

用导数研究报告三次多项式曲线引言在数学中，多项式函数是一类重要的函数。

其中，三次多项式函数的特点是在自变量的三次方次项与一次方次项之间存在关系。

因此，研究三次多项式函数的性质对于数学理论的发展具有重要意义。

导数的定义导数是用来描述函数变化率的工具。

对于函数$f(x)$，它的导数$f'(x)$可以通过以下公式计算：$$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$$三次多项式函数的导数对于三次多项式函数$P(x)$，它的一般形式可以表示为：$$P(x) = ax^3 + bx^2 + cx + d$$其中$a$，$b$，$c$和$d$为常数。

为了研究三次多项式函数的性质，我们需要计算它的导数。

根据导数的定义，可以得到三次多项式函数$P(x)$的导数$P'(x)$：$$P'(x) = 3ax^2 + 2bx + c$$三次多项式曲线的特点通过对三次多项式函数的导数$P'(x)$进行分析，我们可以得到三次多项式曲线的一些特点：1. 曲线的斜率：导数$P'(x)$描述了曲线在不同点上的斜率。

当导数为正时，曲线上升；当导数为负时，曲线下降；当导数为零时，曲线达到极值点。

2. 曲线的拐点：拐点是指曲线从凸向上凹或从凹向上凸变化的点。

在三次多项式曲线上，拐点的位置可以通过导数$P'(x)$的二阶导数来确定。

3. 曲线的极值点：极值点是曲线上最高或最低的点。

在三次多项式曲线上，极值点可以通过导数$P'(x)$的一阶导数为零的点来确定。

结论通过导数的研究，我们可以了解到三次多项式曲线的斜率、拐点和极值点的位置，进而对曲线的形状和性质进行分析。

这为进一步研究和应用三次多项式函数提供了重要的理论基础。

需要注意的是，在实际应用中，有时会出现多个极值点或拐点的情况。

此外，导数可以应用于许多其他数学领域，如最优化问题和微分方程的求解等。

导数法解“三次”函数问题新教材中导数内容的介入，为研究函数的性质提供了新的活力，通过求导可以研究函数的单调性和极值，其操作的步骤学生易掌握，判别的方法也不难。

特别地，当f(x)为三次函数时，通过求导得到的f /(x)为二次函数，且原函数的极值点就是二次函数的零点；同时利用导数的几何意义：曲线在某一点P （00,y x ）处的切线的斜率)(0/x f k =，可得到斜率 k 为关于0x 的二次函数。

根据这些特点，一般三次函数问题，往往可通过求导，转化为二次函数或二次方程问题，然后结合导数的基本知识及二次函数的性质来解决。

下面笔者从课堂或试卷上出现的这一类型题目中选择几例，同时结合学生产生的问题，略作说明。

例1：已知f(x)=d cx bx x +++23在（—∞，0）上是增函数，在[0，2]上是减函数，且方程f(x)=0有三个根，它们分别为α、2、β.（1） 求c 的值；（2） 求证：f(1)≥2（3） 求｜α-β｜的取值范围。

解：（1）,23)(2/c bx x x f ++=由题意可得：x=0为f(x)的极值点，∴0,0)0(/=∴=c f（2）令023)(2/=+=bx x x f ，得32,021b x x -== ∵f(x)在（—∞，0）上是增函数，在[0，2]上是减函数， ∴232≥-b ，即3-≤b 又∵b d d b f 48,048,0)2(--=∴=++∴=∴.2371)1(≥--=++=b d b f（3）∵方程f(x)=0有三个根α、2、β.∴设),)(2()(223n mx x x d cx bx x x f ++-=+++= 由待定系数法得2,2d n b m -=+= ∴α、β为方程02)2(2=-++d x b x 的两根， ∴ α+β=-（b+2），αβ=-d/2；∴｜α-β｜2=16)2(1242)2(222--=--=++b b b d b∵3-≤b ，∴｜α-β｜2≥9，∴｜α-β｜ ≥3一般地，若已知三次函数f(x)=)0(23>+++a d cx bx ax 在（—∞，m ）上是增函数，在[m ，n]上是减函数，在（n,+∞）上是增函数,则二次方程f /(x)=0即0232=++c bx ax 的两个根为m ，n ；且当),(),(+∞⋃-∞∈n m x 时f /(x)>0，当),(n m x ∈时f /(x)<0，反之亦然。

三次函数的导数问题在微积分学中，导数被用于研究函数的变化率。

在下面的文章中，我们将研究三次函数的导数问题。

三次函数的定义三次函数是指具有一次、二次和三次项的函数，可以表示为：f(x) = ax^3 + bx^2 + cx + d其中a、b、c和d是常数。

三次函数的图像通常是一个“S”形的曲线，其形状取决于函数的系数。

具体来说，当a>0时，曲线呈现“下凸”，当a<0时，曲线则呈现“上凸”。

三次函数的导数三次函数的导数通常表示为f'(x)，它是指在某个点x处的切线斜率，也是函数在该点处的变化率。

为了求出三次函数的导数，我们可以使用微积分理论中的求导法则。

具体来说，我们需要求出三次函数的每一项的导数，然后将它们相加。

因此，三次函数的导数可以表示为：f'(x) = 3ax^2 + 2bx + c其中3a、2b和c是三次函数的一次导数项的系数。

三次函数的导数图像三次函数的导数图像通常是一个二次函数，并且其形状与三次函数本身的形状有很大的关系。

当三次函数的a>0时，它的导数图像呈现“上凸”的U形；当a<0时，导数图像则呈现“下凸”的n形。

如果三次函数有其导数为0的点，则该点是函数的临界点，也是函数的最值点之一。

应用三次函数的导数在实际应用中有着广泛的应用。

例如，在物理学中，三次函数可以用来描述物体的加速度变化；在经济学中，三次函数可以用来描述收入和消费之间的关系；在工程学中，三次函数可以用来描述材料的强度和韧性之间的关系等等。

结论通过本文，我们学习了三次函数的导数问题。

我们发现，三次函数的导数是函数变化率的表示，它可以帮助我们更好地理解和使用这些函数。

同时，我们也了解到了三次函数和导数图像的形状及其应用。

三次函数的性质2015年11月13日 意琦行 数海拾贝三次函数（）在高中阶段学习导数后频繁出现，同时也是其他复杂函数的重要组成部分，因此有必要对其性质有所了解，才可以做到知己知彼，百战不殆．性质一 单调性以为例，如图1，记为三次函数图象的判别式，则图1 用判别式判断函数图象当时，为上的单调递增函数；当时，会在中间一段单调递减，形成三个单调区间以及两个极值．性质一的证明 的导函数为其判别式为，进而易得结论．性质二 对称性f (x )=a +b +cx +d x 3x 2a ≠0a >0Δ=−3ac b 2Δ⩽0f (x )R Δ>0f (x )f (x )(x )=3a +2bx +c ,f ′x 24(−3ac )b2如图2，的图象关于点对称（特别地，极值点以及极值点对应的图象上的点也关于对称）．图2 图象的对称性反之，若三次函数的对称中心为，则其解析式可以设为其中．性质二的证明 由于即于是性质二得证．例1 设直线与曲线有三个不同的交点，且，求直线的方程．解 由可知为三次函数的对称中心，由性质二可得，进而不难求得直线的方程．例2 设函数，．（1）求导数，并证明有两个不同的极值点，；f (x )P (−,f(−))b 3a b 3aP (m ,n )f (x )=α⋅+β⋅(x −m )+n ,(x −m )3α≠0f (x )=a +(c −)(x +)−++d ,(x +)b 3a 3b 23a b 3a bc 3a 2b 327a2f (x )=a +(c −)(x +)+f (−),(x +)b 3a 3b 23a b 3a b 3al y =+x +1x 3A ,B ,C |AB |=|BC |=5√l |AB |=|BC |B B (0,1)l y =2x +1f (x )=x (x −1)(x −a )a >1(x )f ′f (x )x 1x 2（2）若不等式成立，求的取值范围．（1）解 的导函数而于是有两个变号零点，从而有两个不同的极值点．（2）解 根据性质二，三次函数的对称中心是两个极值点对应的函数图象上的点的中点．于是即结合，可得的取值范围是．注 本题为2004年高考重庆卷理科数学第题．性质三 切割线性质如图3，设是上任意一点（非对称中心），过作函数图象的一条割线与一条切线（点不为切点），、、均在的图象上，则点的横坐标平分、点的横坐标．f ()+f ()⩽0x 1x 2a f (x )(x )f ′=(x −1)(x −a )+x (x −a )+x (x −1)=3−2(a +1)x +a ,x 2(0)f ′(1)f ′(a )f ′=a >0,=1−a <0,=a (a −1)>0,(x )f ′f (x )(,f ())a +13a +13f ()+f ()=2f ()⩽0,x 1x 2a +132⋅⋅⋅⩽0,a +13a −23−2a +13a >1a [2,+∞)20P f (x )P f (x )AB PT P A B T f (x )T A B图3 切割线性质推论1 设是上任意一点（非对称中心），过作函数图象的两条切线、，切点分别为、，如图．则点的横坐标平分、点的横坐标，如图4．图4 切割线性质推论一推论2 设的极大值为，方程的两根为、（），则区间被和极小值点三等分．图5 切割线性质推论二性质三的证明 设（），直线，直线，则分别将直线与直线的方程与三次函数的解析式联立，得P f (x )P f (x )PM PN M P M P N f (x )M f (x )=M x 1x 2<x 1x 2[,]x 1x 2−b 3af (x )=a +b +cx +d x 3x 2a ≠0PT :y =x +k 0m 0PAB :y =kx +m PT PAB ++(−)+−=0,32于是根据三次方程的韦达定理可得即于是命题得证．推论1和推论2的证明留给读者．例3 如图6，记三次函数（）的图象为，若对于任意非零实数，曲线与其在点处的切线交于另一点，曲线与其在点处的切线交于另一点，线段、与曲线所围成的封闭图形的面积分别记为、．求证：是定值．图6解 由性质二，任意三次函数都可以通过平移变化变成然后可以作伸缩变换变成a +b +(c −)x +d −=0,x 3x 2k 0m 0a +b +(c −k )x +d −m =0,x 3x 22+=++,x T x P x A x B x P =,x T +x A x B 2f (x )=a +b +cx +d x 3x 2a ≠0C x 1C (,f ())P 1x 1x 1(,f ())P 2x 2x 2C P 2(,f ())P 3x 3x 3P 1P 2P 2P 3C S 1S 2S 1S 2f (x )g (x )=p +qx ,x 3而无论平移还是伸缩，题中的均保持不变，因此只需要证明命题对三次函数成立即可．根据题意，联立函数与函数在处的切线方程得于是即又由性质三的推论1，可得即于是，线段与曲线所围成的封闭图形的面积类似的，线段与曲线所围成图形的面积h (x )=+rx ,x 3S 1S 2h (x )=+rx x 3h (x )=+rx x 3h (x )P 1(x −⋅(x −)=0,x 1)2x 22+=0,x 1x 2=−2.x 2x 12=+,x 1x 2x 3=4.x 3x 1P 1P 2C S 1=(x −⋅(x −)d x ∣∣∣∫x 2x 1x 1)2x 2∣∣∣=(−3x +2)d x ∣∣∣∫−2x 1x 1x 3x 21x 31∣∣∣=∣∣∣(−+2x )14x 432x 21x 2x 31∣∣∣−2x 1x 1∣∣∣=,274x 41P 2P 3C于是所求的面积之比为注 此题即2010年高考福建卷理科数学第20题第（2）小问（第（1）小问要求证明该结论对成立）．性质四 切线条数如图7，过的对称中心作切线，则坐标平面被切线和函数的图象分割为四个区域，有以下结论：图7 切线条数① 过区域 I、III 内的点作的切线，有且仅有三条；② 过区域 II、IV 内的点以及对称中心作的切线，有且仅有一条；③ 过切线或函数图象（除去对称中心）上的点作的切线，有且仅有两条．性质四的证明 由性质二，不妨设，坐标平面内一点．三次函数图象上处的切线方程为=,S 2274x 42==.S 1S 2()x 1x 24116f (x )=−x x 3f (x )l l f (x )y =f (x )y =f (x )l f (x )y =f (x )f (x )=+mx x 3P (a ,b )x =t即切线过点，即而三次函数对称中心处的切线方程为于是考虑直线与函数的图象公共点个数．函数的零点为和，且为它的一个极值点，由性质二的推论2知，的另外一个极值点对应的函数图象上的点的坐标为，以为例，的草图如下：容易得到结论：当时，时为个公共点，时为个公共点，时为个公共点；当时，无论取何值，均为个公共点；当时，时为个公共点，y =(3+m )(x −t )++mt ,t 2t 3y =(3+m )x −2,t 2t 3P (a,b )b =−2+3a +ma .t 3t 2y =mx ,y =b −ma h (t )=−2+3a t 3t 2h (t )03a 20h (t )(a ,)a 3a >0h (t )a <0b <+ma ∨b >ma a 31b =ma ∨b =+ma a 32+ma <b <ma a 33a =0b 1a >0b >+ma ∨b <ma a 31时为个公共点，时为个公共点．综上，性质四得证．在高考中，对结论 ① 的考察最为常见，例如2007年高考全国II卷理科数学第22题（压轴题）就是证明性质四的结论 ①：已知函数．（1）求曲线在点处的切线方程；（2）设，如果过点可作曲线的三条切线，证明：．例4 设函数，其中．曲线在点处的切线方程为．（1）确定的值；（2）设曲线在点及处的切线都过点．证明：当时，；（3）若过点可作曲线的三条不同切线，求的取值范围．解 （1）的导函数为于是该函数在处的切线方程为因此b =ma ∨b =+ma a 32ma <b <+ma a 33f (x )=−x x 3y =f (x )M (t ,f (t ))a >0(a ,b )y=f (x )−a <b <f (a )f (x )=−+bx +c 13x 3a 2x 2a >0y =f (x )P (0,f (0))y =1b ,c y =f (x )(,f ())x 1x 1(,f ())x 2x 2(0,2)≠x 1x 2()≠()f ′x 1f ′x 2(0,2)y =f (x )a f (x )(x )=−ax +b ,f ′x 2x =0y =bx +c ,b =0,c =1.（2）函数在处的切线方程为当切线过点时可得于是是该方程的两个不等实根．考虑而两式相减并约去，得而于是f(x )x =t y =(−at )(x −t )+−+1,t 213t 3a 2t 2(0,2)−+1=0,23t 3a 2t 2,x 1x 2()−()f ′x 1f ′x 2=(−a)−(−a )x 21x1x 22x 2=(−)⋅(+−a ),x 1x 2x 1x 2⎧⎩⎨⎪⎪⎪⎪−+1=0,23x 31a2x 21−+1=0,23x 32a2x 22−x 1x 2++=,x 21x 1x 2x 2234a 2++x 21x 1x 2x 22=(+−x 1x 2)2x 1x 2>(+−(+x 1x 2)214x 1x 2)2=(+,34x 1x2)2+≠a ,x 1x 2进而可得（3）函数的对称中心为，于是在对称中心处的切线方程为根据性质四的结论 ①，可得解得即的取值范围是．注 此题为2010年高考湖北卷文科数学第21题（压轴题）． 练习题练习1、已知函数，且．（1）试用含的代数式表示；（2）求的单调区间；（3）令，设函数在（）处取得极值，记点，，证明：线段与曲线存在异于、的公共点．()≠().f ′x 1f ′x 2f (x )(,−+1)a 2a 312y =−(x −)−+1,a 24a 2a 3121<2<−+1,a 324a >2,3√3a (2,+∞)3√3f (x )=+a +bx 13x 3x 2(−1)=0f ′a b f (x )a =−1f (x ),x 1x 2<x 1x 2M (,f ())x 1x 1N (,f ())x 2x 2MN f (x )M N练习2、已知在上是增函数，在上是减函数，且方程有三个根，它们分别为从小到大依次为、、．求的取值范围．练习3、如图8，记原点为点，由点向三次函数（）的图象（记为曲线）引切线，切于不同于点的点，再由点引此曲线的切线，切于不同于点的点．如此继续作下去，得到点列．试回答下列问题：图8（1）求数列的递推公式与初始值；（2）求，并指出点列的极限位置在何处？练习4、已知，过点作图象的切线，如果可以作出三条切线，当时，求点所在的区域面积．练习5、已知函数．（1）求在区间上的最大值；（2）若过点存在条直线与曲线相切，求的取值范围；（3）问过点，，分别存在几条直线与曲线相切？（只需写出结论）f (x )=+b +cx +d x 3x 2(−∞,0)(0,2)f (x )=0α2β|α−β|(,)P 1x 1y 1P 1y =−3a +bx x 3x 2a ≠0C P 1(,)P 2x 2y 2P 2C P 2(,)P 3x 3y 3{(,)}P n x n y n {}x n lim n →+∞x n {}P n f (x )=−x x 3(,)x 0y 0f (x )∈(0,1)x 0(,)x 0y 0f (x )=2−3x x 3f (x )[−2,1]P (1,t )3y =f (x )t A (−1,2)B (2,10)C (0,2)y =f (x )1练习6、已知函数，且．（1）试用含的代数式表示，并求的单调区间；（2）令．设函数在（）处取值极值，记点，，，．请仔细观察曲线在点处的切线与线段的位置变化趋势，并解答以下问题：① 若对任意的，线段与曲线有异于、的公共点，试确定的最小值；② 若存在点，，使得线段与曲线有异于、的公共点，请直接写出的取值范围（不必写出求解过程）．练习题的参考答案练习1、（1）的导函数为于是所求的代数表达式为（2）在（1）的基础上，有于是当时，函数的单调递增区间是和，单调递减区间为；当时，函数的单调递增区间是；f (x )=+a +bx 13x 3x 2(−1)=0f ′a b f (x )a =−1f (x ),x 1x 2<x 1x 2M (,f ())x 1x 1N (,f ())x 2x 2P (m ,f (m ))<m ⩽x 1x 2f (x )P MP m ∈(t ,]x 2MP f (x )P Q t Q (n ,f (n ))⩽n <m x 1PQ f (x )P Q m f (x )(x )=+2ax +b ,f ′x 2b =2a −1.(x )=(x +1)⋅(x +2a −1),f ′a <1f (x )(−∞,−1)(1−2a ,+∞)(−1,1−2a )a =1f (x )R当时，函数的单调递增区间是和，单调递减区间是．（3）此时而于是，．根据性质二，该公共点为三次函数图象的对称中心．注 本题为2009年高考福建卷文科数学第21题（压轴题）．练习2、根据题意，为的导函数的零点，于是．又，于是即从而因此a >1f (x )(−∞,1−2a )(−1,+∞)(1−2a ,−1)f (x )=−−3x ,13x 3x 2(x )=−2x −3,f ′x 2M (−1,)53N (3,−9)f (x )(1,−)113x =0f (x )(x )=3+2bx +cf ′x 2c =0f (2)=08+4b +d =0,d =−4b −8,f (x )=+b −(8+4b )x 3x 2=(x −2)⋅[+(b +2)x +2b +4],x 2222另一方面，由在上是减函数得，即于是可得的取值范围是从而的取值范围是．练习3、（1） 根据已知，联立出发的切线方程与曲线的方程，得又，切线方程只能改变左边三次式的一次项和常数项，于是可得进而由性质三的推论1可得于是数列的递推公式与初始值为（2）由数列的递推公式不难得到通项于是=−4α⋅β=(2−b −16.(α−β)2(α+β)2)2f (x )(0,2)(2)⩽0f ′12+4b ⩽0,b b <−3.|α−β|[3,+∞)P 1C (x −)(x −=0,x 1x 2)2=0x 1=a .x 232∀n ⩾3∧n ∈,2=+.N ∗x n x n −1x n −2{}x n =,n ⩾3∧n ∈,=0,=a .x n +x n −1x n −22N ∗x 1x 232∀n ∈,=a ⋅[1−],N ∗x n (−)12n −1因此点列的极限位置为，也就是三次函数的对称中心．练习4、函数在对称中心处的切线方程为于是根据性质四的结论 ①，我们可得所求区域面积为练习5、（1）的导函数于是可得在区间上的最大值为（2）函数在对称中心处的切线方程为根据性质四的结论 ①，可得即=a .lim n →+∞x n {}P n (a ,−2+ab )a 3f (x )(0,0)y =−x ,[−x −(−x )]d x =d x =.∫10x 3∫10x 314f (x )(x )=6−3,f ′x 2f (x )[−2,1]max {f (−),f (1)}=.2√22√f (x )(0,0)y =−3x ,−3<t <f (1),于是的取值范围是．（3）根据性质四，可得过存在条直线与曲线相切；过存在条直线与曲线相切；过存在条直线与曲线相切．注 本题为2014年高考北京卷文科数学第20题（压轴题）．练习6、（1）；当时，函数的单调递增区间为和，单调递减区间为；当时，函数的单调递增区间为；当时，函数的单调递增区间为和，单调递减区间为．（2）① 的最小值为，证明从略；② 的取值范围为．注 本题为2009年高考福建卷理科数学第21题（压轴题）．−3<t <−1,t (−3,−1)A (−1,2)3y =f (x )B (2,10)2y =f (x )C (0,2)1y =f (x )b =2a −1a >1f (x )(−∞,1−2a )(−1,+∞)(1−2a ,−1)a =1f (x )R a <1f (x )(−∞,−1)(1−2a ,+∞)(−1,1−2a )t 2m (1,3]。

3次函数曲线-概述说明以及解释1.引言1.1 概述概述在数学中，三次函数是一种常见的多项式函数，其最高次项的指数为3。

三次函数的一般形式可以表示为y = ax^3 + bx^2 + cx + d，其中a、b、c和d都是实数，并且a不等于0。

三次函数曲线通常呈现出一种典型的"弓形"形状，有时可能具有一个局部极值点或者一个拐点。

它们在图像上的走势和特点在多个领域中都有重要的应用，例如物理学、经济学和计算机图形学等。

理解和掌握三次函数曲线的特点对于解决实际问题和进行进一步的数学研究都是非常重要的。

本文将围绕三次函数曲线展开讨论，首先介绍三次函数的基本定义和性质，然后探讨三次函数曲线的图像特点以及如何进行函数图像的变换和分析。

接下来，我们将进一步研究三次函数曲线的局部极值点和拐点的性质，并举例说明在实际问题中的应用。

最后，我们将总结所讨论的内容，并展望一些可能的研究方向。

通过研究和理解三次函数曲线的性质和特点，我们可以更好地应用它们解决实际问题，并且有助于我们对数学的深入理解和进一步研究。

接下来，我们将详细介绍本文的组织结构和目的。

1.2 文章结构2. 正文在本文中，我们将着重研究3次函数曲线。

通过对这种特殊类型的函数曲线进行深入的分析和研究，我们可以更好地理解它们的数学性质和应用。

本文的正文部分将分为三个要点来探讨3次函数曲线所涉及的关键概念和性质。

2.1 第一要点在第一要点中，我们将首先介绍3次函数曲线的基本定义和表达形式。

我们将学习如何根据给定的系数，利用函数表达式来绘制3次函数曲线的图像。

此外，我们还将讨论3次函数曲线的对称性和奇偶性，并探索其在数学和科学领域中的实际应用。

2.2 第二要点在第二要点中，我们将进一步研究3次函数曲线的性质和特征。

我们将通过对曲线的导数和导数变化率的分析，探讨曲线的增减性和凸凹性。

此外，我们还将介绍曲线的转折点和拐点，并讨论这些特殊点对曲线整体形状的影响。