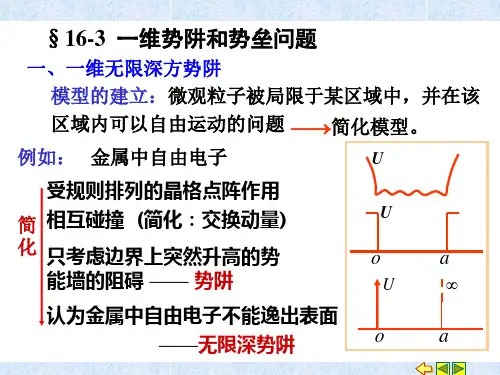
16-3一维势阱和势垒问题解读
- 格式:ppt
- 大小:1.10 MB
- 文档页数:36






一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数,对以上的透射系数的总结,推出了对于任意势垒中透射系数, 并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中,遇到的问题和 值得注意的地方。
在求方势垒波 函数中,首先要知道这是一个什 么样问题,满足什么样的方程, 方程可以写成什么样的形式,在 求解方程中,波函数的形式应该怎样需要怎样的分段,分段的过程中,特别要强调的边界条件问题。
并且验证了概率流密度。
在量子力学中,粒子在势垒附近发生的现象是不一样的,能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射,而能量小于0u 的粒子也会有部分穿过势垒,这在经典力学中是不会发生的。
下面讨论的是一维散射(即在非束缚态下问题,在无穷远处波函数不趋于零)。
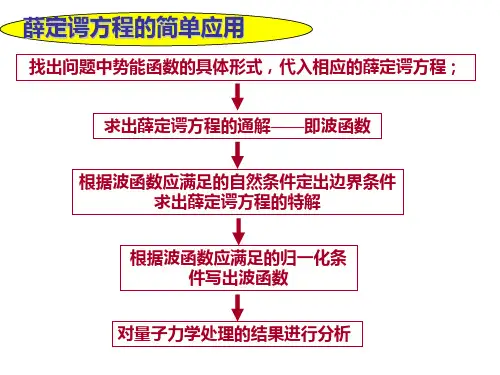
重点讨论的是粒子通过势垒的透射和反射,重点在于求出波函数,这就必须求解薛定谔方程,由于)(x U 是与时间无关的,此处是定态薛定谔方程。
定态薛定谔方程通式:ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域:⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h (1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注: 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时,通解xq xq eC e C y ---+=21,当0>q 时,通解xq ixq ie C e C y -+=21方程(1)的解可以表示为:⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ (2)定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-,可以看到式子(2)的三式,第一项是左向右传播的平面波,第二项是由右向左传播的平面波,即入射波和反射波。


一维势垒问题总结
一维势垒问题是指在一维空间中存在一个势能障碍的物理问题。
该问题涉及到粒子的运动和势能的影响,有着广泛的应用。
一维势垒问题的主要特点是势能障碍的存在。
这个势能障碍可以是有限高度的,也可以是无限高度的。
有限高度的势能障碍表示粒子可以跨越势垒,而无限高度的势能障碍表示粒子无法穿越势垒。
在求解一维势垒问题时,需要考虑的主要因素包括粒子的动能和势能。
根据量子力学的原理,粒子在势垒两侧会存在反射和透射两种情况。
对于势能障碍的高度低于粒子的能量,粒子可以自由穿越势垒,这称为透射现象。
透射的概率可以通过隧道效应来描述,隧道效应可以用量子力学中的波函数来解释。
对于势能障碍的高度高于粒子的能量,粒子会发生反射现象。
在经典力学中,反射的概率可以通过粒子的入射能量和势垒高度之间的关系来计算。
对于无限高度的势能障碍,粒子无法穿越势垒,只能发生反射现象。
这种情况下,粒子的能量必须超过势能障碍的高度才能透过。
一维势垒问题在物理学和化学领域都有广泛的应用。
例如,它可以用于解释原子核中的核反应、电子在导体中的传输等。
总之,一维势垒问题是涉及势能障碍的物理问题,涉及粒子的运动和势能的影响。
求解该问题需要考虑粒子的动能和势能,以及透射和反射两种现象。
一维势垒问题在科学研究中具有重要的应用价值。
一维无限深势阱定义编辑粒子在一种简单外力场中做一维运动,其势能函数为U(X)=0 (-a<x<a);U(x)=∞ (x≥a或x≤-a)。
由于其函数图形像阱,且势能在一定区域为0,而在此区域外势能为无穷大,所以这种势能分布叫做一维无限深势阱。
实际模型编辑自由电子在一块金属中的运动相当于在势阱中的运动。
在阱内,由于势能为零,粒子受到的总的力为零,其运动是自由的。
在边界上x=0或x=a处,由于势能突然增加到无限大,粒子受到无限大指向阱内的力。
因此,粒子的位置不可能到达0<x<a的范围以外。
一维无限深势阱中粒子运动的波函数编辑一维无限深势阱中粒子运动的波函数为Ψ(x)=√(2/a)·sin(nπx/a) (0<x<a)。
三、一维势阱3.1 一维无限深势阱要使电子脱离金属,需要对它做功,这相当于电子在金属表面处势能突然增大,自由电子在金属内部的运动,可近似比作在无限深势阱的运动。
由于金属是各向同性的,便可简化为电子在一维无限深势阱中的运动。
势能曲线如右图,势能表达式为电子在一维无限深势阱中运动,用经典力学描述和量子力学描述得到了完全不同的结果。
按照经典概念,当外界向它提供能量时,电子可获得此能量而自身能量发生连续变化。
电子在阱内任何位置出现的概率也是相等的。
然而,按照量子力学观点,它的行为却不是这样的。
(1) 定态薛定谔方程的解电子所受的保守力,在边界处电子所受的力无限大,指向阱内,意味着电子不可能越出阱外,由波函数物理意义可知势阱外波函数。
电子在势阱内势能为零,受力为零。
势阱内定态薛定谔方程为令方程变为其解为根据波函数应满足的标准化条件,波函数应在边界x=0和x=a上连续得应用归一化条件求得于是定态波函数为(2) 能量量子化因,合并(23.3.3)式,即得到一维无限深势阱中的电子能量上式表明:电子的能量不能连续地取任意值,只能取分立值,即能量是量子化的,可形象地称为处于相应的能级(如右图所示)。