当前位置：文档之家 › 一维有限深方势阱和势垒贯穿

一维有限深方势阱和势垒贯穿

  • 格式：ppt
  • 大小：1.05 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

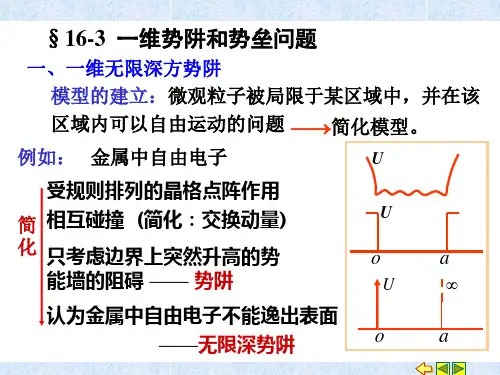
16-3 一维势阱和势垒问题

16-3 一维势阱和势垒问题

]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波： 由 x > a 处无反射波： B 3 = 0 令 A1 = 1（以入射波强度为标准） 以入射波强度为标准） 由波函数的 标准条件得 O 可解得
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立：微观粒子被局限于某区域中， 模型的建立：微观粒子被局限于某区域中，并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如： 例如： 金属中自由电子 受规则排列的晶格点阵作用 简化：交换动量) 简 相互碰撞 (简化：交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习： 练习
已知： 已知：
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞

势垒贯穿与应用解读

势垒贯穿与应用解读

势垒贯穿与应用 势垒贯穿设一个质量为m 的粒子，沿x 轴正方向运动，其势能为： U(x)=0 x<0 和x>a U(x)=U 0 0≤x ≤a这种势能分布称为一维势垒。

粒子在 x < 0 区域里，若其能量小于势垒高度，经典物理来看是不能越过势垒达到 x > a 的区域。

在量子力学中，情况又如果呢？为讨论方便，我们把整个空间分成三个区域： 在各个区域的波函数分别表示为ψ1 ψ2 ψ3三个区间的薛定谔方程简化为：求出解的形式是)(),0(),0(a x a x x ≥I ∏≤≤∏≤I ),()(212122x E dx x d m ϕϕ=- 0≤x ),()()(22202222x E x U dxx d m ϕϕϕ=+- ax ≤≤0),()(232322x E dxx d m ϕϕ=- a x ≥222 mEk =2021)(2 E U m k -=,0)()(12212≤=+x x k dxx d ϕϕa x x k dxx d ≤≤=-0,0)()(221222ϕϕa x x k dxx d ≥=+,0)()(32232ϕϕikxikx e A Ae -'+=ψ1x ik Be 12+=ψikx Ce =ψ3O(1)E>U 0按照经典力学观点,在E>U 0情况下，粒子应畅通无阻地全部通过势垒，而不会在势垒壁上发生反射而在微观粒子的情形，却会发生反射。

(2)E<U 0从解薛定谔方程的结果来看，在势垒内部存在波函数ψ。

即在势垒内部找出粒子的概率不为零，同时，在x>a 区域也存在波函数，所以粒子还可能穿过势垒进入x>a 区域粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应定义粒子穿过势垒的贯穿系数是：透射波的概率密度与入射波概率密度的比值。

势垒高度U 0越低、势垒宽a 度越小，则粒子穿过势垒的概率就越大。

隧道效应是经典力学所无法解释的由于电子的隧道效应，金属中的电子并不完全局限于表面边界之内，电子密度并不在表面边界处突变为零，而是在表面以外呈指数形式衰减，衰减长度约为1nm只要将原子线度的极细探针以及被研究物质的表面作为两个电极，当样品与针尖的距离非常接近时，它们的表面电子云就可能重叠若在样品与针尖之间加一微小电压U b 电子就会穿过电极间的势垒形成隧道电流。

第十八章4一维势阱势垒

第十八章4一维势阱势垒

求解定态薛定谔方程 2 2 h dψ − = Eψ (0 < x < a) 2
d2ψ(x) 2 + k ψ(x) = 0 2 dx ψ(x) = Asinkx + Bcoskx
由于阱壁无限高， 由于阱壁无限高，所以 ψ(0) = 0 阱壁无限高
ψ(a) = 0
Asin(0) + Bcos(0) = 0 Asin(a) + Bcos(a) = 0
Φn ( x) = a sin a
2
a
a
x, n = 1,2,3,⋅ ⋅ ⋅
En =
π 2h2
2ma
2
n , n = 1,2,3,⋅ ⋅ ⋅
10
则
Ψ( x) = C f ( x)
1 2 πx 2 2πx sin − sin = 2 a a a a 1 1 = Φ1 ( x) − Φ2 ( x) 2 2
时、空异号 为右行波
15
求出解的形式画于图中。 求出解的形式画于图中。 定义粒子穿过势垒的贯穿系数： 定义粒子穿过势垒的贯穿系数
隧道效应
I
II
III
势垒的宽度约50nm 以上时， 以上时， 当 时，势垒的宽度约 贯穿系数会小六个数量级以上。 贯穿系数会小六个数量级以上。隧道效应在 实际上已经没有意义了。量子概念过渡到经典了。 实际上已经没有意义了。量子概念过渡到经典了。
En = (
πh
2
2 2
2m a
)n , n = 1, 2, 3⋅ ⋅ ⋅
2
4
En = (
πh
2
2 2
2m a
)n , n = 1, 2, 3⋅ ⋅ ⋅
2

16-3一维势阱和势垒问题解读

16-3一维势阱和势垒问题解读
n4
x a
a x
第k激发态(n=k+1)有k个节点。
（2）一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰：量子 经典均匀分布 0
a a n 1，x 处，几率最大 0 3 2 b n ，峰数 ，当n 时，
4
U0
II
III
o
a
x
而在微观粒子的情形，却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
（2）E<U0 从解薛定谔方程的结果来看，在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零，同时，在 x>a区域也存在波函数，所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数，由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑，粒子不可能透过阱壁，因而按照波 函数的统计诠释，要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况，即
(0) 0, (a) 0
————边界条件
(0) 0
这说明：并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件，只有当能量取上式 给出的那些分立的值 En（体系的能量本征值）时， 相应的波函数才是物理上有意义的，即本问题中体系 的能量是量子化的，亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a

【大学物理】§3-2薛定谔方程 一维势阱和势垒问题

【大学物理】§3-2薛定谔方程 一维势阱和势垒问题
§2-3 薛定谔方程
一、一维无限深方势阱
对于一维无限深方势阱有
一维势阱和势垒问题
∞
∞
U(x)
U
(
x)
0
(0 x a) ( 0 x, x a)
势阱内U(x) = 0，哈密顿算符为
H
2
2
d2 d x2
定态薛定谔方程为
0
a
令
2E
k
薛定谔方程的解为
d 2
d x2
2E
2
0
(x) Asin(kx )
由此解得最大值得位置为
x (2N 1) a 2n
例如
n 1, N 0
最大值位置
x 1a 2
n 2, N 0,1, 最大值位置 x 1 a , 3 a Nhomakorabea44
n 3, N 0,1, 2, 最大值位置 x 1 a , 3 a , 5 a.
6 66
可见，概率密度最大值的数目和量子数n相等。
10
2m dx2
2. 波函数
(
x)
2 sin( n x), 0 x a
aa
0,
x 0或x a
3. 能量
En
n
2
22
2ma 2
n 1,2,3
4. 概率密度
(x) 2 2 sin 2 ( n π x)
a
a
4
讨论
n (x)
2 sin n x
a a
(0 x a)
1.n=0给出的波函数
1
根据 (0，)可以0确定 = 0或m，m =1,2,3,。于是上式改写为
根据 (a) 0，得
(x) Asin kx
ka = n， n = 1,2,3, ···

一维无限深势阱

一维无限深势阱

A e ikx B e ikx , ( x ) F e k3 x G e k3 x , C e ikx ,
2 2
x0 0 xa xa
(k k3 ) sh k3a B 2 , 2 A (k k3 ) shk3a 2ikk3chk3a
1 x x 1 x x shx (e e ), chx (e e ). 2 2
ik1 x
2
x0 0 xa xa
2 Beik x B e ik x
ik1 x 3 Ce C e (C 0) ik1 x
这里 k1 因子
ikx e 波数为K的平面波， 则是向左运动的平面波。在I、II两
x 0,
2mE ，k 2 2m( E V0 ) 。考虑到时间 ikx iEt / i t ，因此 代表向右运动的 e e
2
1 2
所以几率密度与 (1
2
/a )
2

1 2
成比例。
一、方势垒
1.方势垒是：
§3.3势垒贯穿 U(x)
U0
x 0 or 0, U ( x) U 0 0 0 x a
xa
0 a x
其特点是： (1)对于势阱，波函数在无穷远处趋于零，能谱是分立的。但 对于势垒，波函数在无穷远处不为零。下面将看到，粒子能量 可取任意值。 (2)按照经典力学观点，若E<U0 ,则粒子不能进入势垒,在x=0处 全被弹回；若 E> U0, 则粒子将穿过势垒运动。 但从量子力学的观点，由于粒子的波动性，此问题将与波 透过一层介质相似，总有一部分波穿过势垒，而有一部分波被 反射回去。因此，讨论的重点是反射和透射系数。

一一一维维维势势势垒垒垒贯贯贯穿穿穿

一一一维维维势势势垒垒垒贯贯贯穿穿穿
2 ˆ (x) = − � ψ (x)�� = Eψ (x) Hψ 2m
(2.88)
(2.89)
在x < 0, x > a的区域, 就是 ψ (x) + k = 0, 在0 ≤ x ≤ a, ψ (x) − β = 0,
�� 2 �� 2
k=
�
2mE �2
(2.90)
β=
�
2m(V0 − E ) . �2
.
(2.106)
2.4. 一维势垒贯穿
37
在以上计算的基础上, 我们来讨论些物理问题. 首先我们看到S 不等于零! 这意味着我们可以在势垒的右边找到粒子! 这一完 全不同于经典力学的结论称为隧 道 效 应 (tunneling effect). 下面作更详细的分析. 在势垒左边, x < 0区域, 我们可以计算几率流密度j . j= 1 ˆψ − ψ p ˆψ ∗ ), (ψ ∗ p 2m (2.107)
2 sinh2 βa V0 4E (V0 −E )
CHAPTER 2. 一维问题
= =
A + B, (A − B )β.
(2.95)
= =
Байду номын сангаас
Seika , ikSeika
(2.96)
= =
β + ik + R(β − ik ) β − ik + R(β + ik ). (2.97)
= =
eika−βa S (β + ik ) eika+βa S (β − ik ).
2 sin2 αa V0 4E (E −V0 )
(2.111) . (2.112)
我们应该可以观察到所谓的共振透射。当αa = nπ , n = 1, 2, 3, · · · , |S |2 = 1. 如果粒子遇到一个势井，V0 < 0, 会怎样？(2.112)仍然适用。唯一要注意的 是：当E → 0, T → 0.

16-3 一维势阱和势垒问题

16-3 一维势阱和势垒问题

ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为：
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高 所以粒子不能穿透势壁 理由 因为势壁无限高,所以粒子不能穿透势壁 故势 因为势壁无限高 所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量，E > 0，令 是粒子的总能量， 是粒子的总能量 ， 定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为： 谔方程简化为： d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式 ：
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式 ： ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动， 限高势壁间运动，这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关， 因为系统的势能与时间无关，因此这是一个定 态问题，可以用定态薛定谔方程进行求解。 态问题，可以用定态薛定谔方程进行求解。

一维势阱和势垒问题

一维势阱和势垒问题
§16-3 一维势阱和势垒问题
1.一维无限深势阱
一维无限深方势阱是金属中自由电子的简化模型
粒子在势阱内受力为零，势能为零。在阱内自由运 动。在阱外势能为无穷大，在阱壁上受极大的斥力, 不能到阱外。
一维无限深方势阱的数学表达形式 ：
0 (0 x a) U (x) (x 0及x a )
无数峰：量子 经典均匀0分布4 2
a
n4
x
0
ax
n时
量子经典
|n | 2 n很大
En
0
a
一维无限深势阱
En n
n(x)
En ( x)

h2 8ma 2
n2
n (x)
2 sin n x
aa
n(x)

2 sin2( n
aa
x)
0
ax
例1: 证明无限深方势阱中，不同能级的粒子波函数 具有正交性：
0 x a;
0,
x 0, x a.
讨论：
① 粒子的能量
En

2k 2
2

22n2
2 a2
,
n 1,2,3,
粒子的最低能量状态称为基态，则一维无限深方势 阱的基态能量为：
E1
22 2a2
0
————零点能
与零点能相对应的，应存在零点运动。这与经典粒
子的运动是相矛盾的。零点能是微观粒子波动性的表 现，因为“静止的波”是没有意义的。
② 图形
一维无限深方势阱中粒子的能级、波函数和几率密度
（2 sin nx , 0 x a;
a a
0,
x 0, x a. 0
除端点外，

量子力学专题三（一维势场中的粒子）

量子力学专题三（一维势场中的粒子）

量⼦⼒学专题三（⼀维势场中的粒⼦）量⼦⼒学专题三：⼀维势场中的粒⼦⼀、⼀维薛定谔⽅程边界条件和处理办法（熟练掌握）1、边界条件：A、束缚态边界条件：在⽆穷远处，找到粒⼦的概率为零，相应的波函数的值应该趋近于零；B、连续性边条件：a、波函数连续；b、波函数的⼀阶偏导数连续。

（注意：不⼀定同时成⽴！！）C、周期性边界条件：在求解⾓动量l分量的本征函数时，利⽤周期性边界条件可以确z定本征函数的归⼀化常数；在求解转⼦的能量本征函数时，亦可以利⽤周期性边界条件来确定其归⼀化常数。

2、处理⽅法：A、列出不同区间的能量本征⽅程，并对其进⾏求解；B、根据束缚态边条件，选择适合的解；C、根据连续性边条件，对得到的波函数进⾏归⼀化处理；D、写出本征函数和对应的能量本征值。

⼆、⼀维⽅势阱：1、⼀维⽆限深⽅势阱的求解⽅法及其物理讨论（熟练掌握） A 、⾮对称势阱： a 、解题步骤：（1）写出各个区间的能量本⾏⽅程；（2）根据写出的微分⽅程，求出其通解；（3）根据连续性边界条件，确定其相位及其能量本征值的取值；（4）根据概率诠释，对波函数进⾏归⼀化处理，确定待定常数；（5）写出能量本征⽅程和对应的能量本征值。

b 、具体过程：)0(),0(0)(a x a x x x V <<>∞=（1）列出不同区间的能量本征⽅程，并对其进⾏求解；在0区间，波函数为：0)(≡x ψ在ax <<0区间，能量本征⽅程为：)()(2222x E x dxdm ψψ=-对其变形，得2=+''ψψk其中，mE k2=（0>E ）。

解得： )sin()(δψ+=kx A x（2）根据束缚态边条件，选择适合的解；此处的束缚态边条件，即粒⼦在⽆穷远处出现的概率为零，在求解本征⽅程——在0区间，波函数为：0)(≡x ψ——时已经应⽤了！（3）根据连续性边条件，对得到的波函数进⾏归⼀化处理；在0=x 处，波函数连续，有0sin )0(==δψA ，则有0=δ。

一维有限深方势阱和势垒贯穿汇编

一维有限深方势阱和势垒贯穿汇编
讨论
从一维无限深方势阱 理解有限深方势阱
k2
2mE
2
V (x)
ka n n 1,2,3,
o
En
2 2
2ma 2
n2
n 1,2,3,
V (x) 0,
V (x) ,
ax
0 xa x 0, x a
E1
2 2
2ma2
1 2
2 2
ma2
,
微观能量尺度可以选取 2 2
ma2
微观动量尺度
ka = n
-a/2 a/2 x
对于参考书p47页说明
a)不在讨论为什么势能对称，波函数也对称了。 b) 公式29和30实质上是利用
c) 估计一下公式32的数值大小？ d)纵轴取决于势阱高度，横轴取决于能量，此处
是势阱内部动能。我们让动能变化，看看什 么时候能冲破势阱束缚。
公式右面=
U0 22
U0
2 2
2
STM样品必须具有一定程度的导电性； 在恒流工作模式下有时对表面某些沟 槽不能准确探测。任何一种技术都有 其局限性。
dx2
V0 2
(x)
E2 (x),
定态薛定谔方程 的解又如何呢？
0 xa
2 2m
d
23 (x)
dx2
E3
( x),
xa
令：
k
2
Байду номын сангаас
2mE 2
k12
2m(V0 2
E)
三个区间的薛定谔方程化为：
V
V0
d
21(
dx2
x)
k
21
(
x)
0,
x0
I
d

一维定态问题无限深方势阱

一维定态问题无限深方势阱

u(x)
2
=
2
sin 2
nπ
a a
0
x, ,
0≤ x≤a x < 0,or, x > a
n = 1, 2,3,
概率分布不均匀，存在概率为零的节点。 但：概率分布不随时间变化！
§2.4 一维定态问题–无限深方势阱
结论：
(3) 束缚在势阱中的粒子的能量是量子化的
=E
E=n
π2 2
2ma2
n2 ,
平均值
∫ = E
+∞
ψ
−∞
*
(r
,
t
)
−
2
2m
∇2
+V
(r,t) ψ
(r , t )dτ
总能能算符：
Hˆ
=−
2
∇2
+V
(r,t)
pˆ 2 =
+V (r,t)
2m
2m
称为粒子的哈密顿算符。
§2.5 力学量的平均值、算符表示—平均值
含时薛定谔方程：
i
∂ψ
∂t
=
−
2
2m
∇2
+ V (r,t) ψ
(1) 粒子的位置 r
例如：一维无限深方势阱
粒子的位置是不确定的，取值在[0, a]之间。 但粒子的概率分布是确定的，是
u(x)
2
=
2 sin2 nπ a a 0
x, ,
0≤ x≤a x < 0,or, x > a
n = 1, 2,3,
所以，可以得到粒子位置的平均值 (假设粒子处在基态 n =1 态)：
2
∇2 2m
+ V (r,t)ψ

一维无限深势阱 隧 道 效 应 东北大学 大学物理 - 副本

一维无限深势阱 隧 道 效 应 东北大学 大学物理 - 副本

2
n
a
x
En
n2
h2 8ma2
(n 1, 2, ... )
一、一维无限深势阱
一维无限深势阱中粒子的能级、波函数和概率密度
En n=3
w3
En E3 9E1
n 3
2 sin 3 x
aa
w2
n=2
E2 4E1
n=1 0
w1
a
E1
h2 8ma2
x
0
2
2 sin 2 x
aa
1
2 sin x
aa
2
sin
n
x)e
i
Ent
,
aa
(0 x a)
0,
(0 x, x a)
一、一维无限深势阱
1、势阱中粒子的波函数
一维无限深势阱中粒子的波函数：
(x)
2 sin n x,
aa
(0 x a)
0,
(0 x, x a)
概率密度函数：
w( x)
Ψ
2
(x) 2
2 a
sin
2
n
a
x,
(0 x a)
ax
一、一维无限深势阱
3、势阱中粒子的波函数的驻波特点
x 0 和 x a 处，
波函数的值皆为零。 波函数以驻波形式存在势阱中：
a n (n 1, 2, ... )
2
n
2a n
pn
h
n
nh 2a
n 4
n4
4 3 n3
2
3
n2
1
2
n 1
1 / 2
o
a
一、一维无限深势阱
3、势阱中粒子的波函数的驻波特点

量子力学 一维无限深方势阱,线性谐振子,势垒贯穿

量子力学 一维无限深方势阱,线性谐振子,势垒贯穿

(7)
由此得到，
Asin a 0,
B cos a 0
(8)
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
A 和 B 不能同时为零，否则 y 处处为零。因此，
A 0, B 0, cos a 0 sin a 0
(9) (10)
由此可求得：
n a , 2
(2n 1) 2 h2 En En1 En ， 8ma 2
a)、 En µ n 2 ，当 n ® ¥时，
DEn 1 n®¥ ~ ¾ ¾¾ ®0 En n
正如对应原理所示大量子数极限下量子理论将逐渐 逼近经典理论。
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
b)、 DEn µ
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
一维无限深势阱的能量本征函数一维无限深势阱中粒子位置几率密度分布
第二章 波函数和薛定谔方程 2.7、 线性谐振子
2.7.1、谐振子模型
2.7、 线性谐振子 2.7.1、谐振子模型 经典力学中，当质量为 m 的粒子受到弹性力 F kx 作 用，其运动方程为，
考察上式解的渐进行为，当
很大时， 与 相比可
以忽略，方程（4）可以近似表示为：
d 2 2 0 2 d
(5)
第二章 波函数和薛定谔方程 2.7、 线性谐振子
2.7.2、 线性谐振子的能量本征值问题
不难证明，
时， ~ e
2
/2
，
~ e
第二章 波函数和薛定谔方程
第二章 波函数和薛定谔方程
第三部分、一维无限深方势阱，线性谐振子，势垒贯穿
第二章 波函数和薛定谔方程 引言

无限深方势阱,势垒贯穿 - 温州大学 - 物理与电子信息工程学院

无限深方势阱,势垒贯穿 - 温州大学 - 物理与电子信息工程学院

答案：t g ka=- k/k1
2m E k 2
2m(V 0 E ) k1 2
kx
若k用ik代入,则微分方 程变为： 其解为：
1 Ae
Be
kx
本节内容：
• 介绍一个粒子分别在2种方位势下： 一维无限深方势阱, 有限深对称方势阱 如何用薛定谔方程求解
• 对束缚态与分立谱作一些讨论。
目的是以一维定态为例，通过求解已知势场的 定态薛定谔方程，了解怎样确定定态的能量E、波函 数，从而看出能量量子化是薛定谔方程的自然结果。
3.2.3
束缚态与分立谱的讨论
基本思想，对于束缚态（无穷远处波函数 为0），只有能量为某些值时，波函数在 x=±a/2处才能光滑连接起来。
作业－7
d 2 ( x) 2 1、求证微分方程 k ( x) 0 有三种等价解 2 dx
A）
B） 2 C sin kx D coskx C）
3.2.1 一维无限深方势阱
一维无限深方势阱：
0, V ( x) ,
0 xa ; x 0, x a,
V ( x)
金属中的电子可近似看成处在 一维有限深方势阱中运动。
其定态薛定谔方程：
2 d 2 ( x) V ( x) ( x) E ( x) 2 2m dx
联立求解。 用作图法（图3.3a) 可求能量E。
在奇宇称态下，要求波函数ψ与其一阶导数ψ΄在x=a/2连续（在x=a/2连续的结果相同），得：
得
k cot(ka / 2) 2 2 2 2 mV a / 2 cot ，联立 0
同样用作图法（图3.3b) 可求出另一能量E。
仅讨论束缚态（0＜E＜V0）情况。

一维无限深势阱

一维无限深势阱
因而，
(at x a) (at x a)
Acos ka 0,
B sin
ka
0.
有两种情形的解：
（1） B 0, coska 0, 所以，
(n 1 )
k 2 , a
(n 0,1,2, )
E
2 2 2a 2
n
12
2
,
(
x)
A cos
n
12
x
a
.
(偶宇称)
(2) A 0,sin ka 0 所以，
0
显然E必须>0，所以记
(a x a)
2E
k
那么方程变成： d 2
dx 2
k 2 (x)
0.
它的一般解是：
(x) Acos kx Bsin kx.
(a x a)
这三段的解必须在 x=±a 处衔接起来。在势能有无限
大跳跃的地方，衔接条件只有 本身的连续性。所以
现在
Acos ka Bsin ka 0, Acos ka Bsin ka 0,
n
k , a
(n 1,2,3, )
E
2 2 2a 2
n2,
( x) B sin nx .
a
（奇宇称）
二者合起来可写为：
n
kn 2a ,
(n 1,2,3, )
En
2 2 8a 2
n2,
n n (x) An sin 2a (x a).
波函数的归一化是：
所以，
a | (x) |2dx 1 a
R
B2 A2
(k 2
(k 2 k32 )2 sh 2k3a k32 )2 sh 2k3a 4k 2k32
,

52_6半无限深势阱_一维势垒解读

52_6半无限深势阱_一维势垒解读

4. 反馈：保持i不变
d不变（不撞坏针尖）
17
显示器
压电 控制 加电压 反馈传 感器 隧道 电流
参考信号
扫描隧道显微镜示意图
18
用STM得到的神经细胞象
用 AFM 得到的癌细 胞 的表面图象
19
1991年 恩格勒等用STM在镍单晶表面遂个移 动氙原子拚成了字母IBM，每个字母长5纳米，
20
1991 年 2 月 IBM的“原子书 法”小组又创造出“分子 绘画”艺术— “CO 小人” 图中每个白团是单个 CO分子竖 在铂片表面上的图象，上端为 氧原子， CO分子的间距：0.5 nm； “分子人”身高：5 nm， 堪称为世界上最小的“小人图”

2
2mE k 2
2
sin ( ka ) 1或
2
ka
h2 E U0 2 2 8ma 32ma
2 2
( x) Be
x
,
xa
结果说明粒子会出现在x＝a的表层附近
6
§6 一维方势垒 势垒贯穿（隧道效应） U
U ( x ) 0, x 0, x a
23
隧道效应应用之二 * 核的衰变
是通过 隧道效应出来的
U
35MeV
238
U
234
Th + He
4
库仑势能
E 4.25MeV
对不同的核，算出的 衰变概率和实验一致。 0 R
4.25MeV

r
核力势能
24
x 0, x a
n 1,2,3, 0 xa
一维无限深方势阱
n ( x) 0,
n ( x)
2
2 nx sin( ), a a

§2.8势垒贯穿解读

§2.8势垒贯穿解读

2 2 1 3 2 3
隧道效应的本质: 来源于微观粒子的波粒二相性
1981年IBM公司苏黎世实验室的两位科学家宾尼希(G．Binnig) 和罗雷尔(H．Roher)利用电子的隧道效应制成了扫描遂穿显微 镜 ( Scanning Tunneling Microscope)——观察固体表面原子情 况的超高倍显微镜。
透射几率流密度 J D D 入射几率流密度 J
——表示透过势垒的概率
反射几率流密度 J R R 入射几率流密度 J
——表示被势垒反射回去的概率
2 J D | C |2 4k12 k 2 D 2 2 2 2 2 J | A| (k1 k 2 ) sin 2 ak2 4k12 k 2
J R | A'|2 (k12 k 22 ) 2 sin 2 k 2 a R 2 2 2 2 1 D 2 2 2 J | A | (k1 k 2 ) sin ak2 4k1 k 2
说明入射粒子一部分贯穿到x>a区域，另一部分 被势垒反射回去，即 E U 0 的粒子也有可能被 反射回去
图象处理系统 扫描探针 样品表面电子云

STM具有空间的高分辨率(横向可达0.1nm， 纵向可优于0．01nm)，能直接观察到物质表 面的原子结构，把人们带到了微观世界。
纳米算盘
硅表面， 每一个隆起处是一个硅原子
原子组成的“原子”
单原子操纵1990年4月，美国IBM宣布，他 们用扫描隧道显微镜操纵氙原子，用35个 原子排出了"IBM"字样
2. E U 0 时——粒子是否有越过势垒的概率？ ——即看透射系数是否为零？！
d2 2 2 E 0 ，( x 0, x a) ——与前相同 2 dx

21.7 一维势阱 势垒 隧道效应

21.7 一维势阱 势垒 隧道效应

STM的发明者 宾尼、罗雷尔和电 子显微镜的发明者 卢斯卡分享了1986 年诺贝尔物理奖。
宾尼
罗雷尔
U0
电子云重叠 U0 U0 E
样 品
d
针 尖
扫描隧道显微镜（STM）装置示意图
用STM得到的神经细胞象
液体中观察原子图象
在电解液中得到的硫酸根离子吸附在铜 单晶表面的STM图象。
“扫描隧道绘画 ” 一氧化碳“分子人”
8 n1 x n2 y n3 z ( x, y, z ) sin sin sin l1l2 l3 l1 l2 l3
三维势阱中粒子的能量：
n12 2 2 n2 2 2 2 n32 2 2 E 2 2 2 2ml1 2ml2 2ml3
处在超晶格的一维量子线和两维量子阱中的电子 就属于一维和两维势阱中的粒子，而处在金属内的电 子可看作三维势阱中的粒子。
i En t
)e
i En t

( px En t )
C 2e
( px En t )
n ( x, t ) 是由两个沿相反方向传播的平面波叠加而
③粒子在阱中的分布 经典力学的结果：均匀分布 P ( x ) 1/ a a a P ( x)dx P ( x) dx P ( x)a 1
(4) 解方程、定常数 在 0<x<a 区域，定态薛定谔方程为
令
d x 2mE 2 x 0 2 dx 2mE 2 k 2 d 2 x 2 k x 0 2 dx
2
比较谐振动方程 特解为
d2x 2 x0 2 dt
( x ) C sin(kx )
2 2 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x0

2 2m
d
22 (x)
dx2
V0 2
(x)

E2 (x),
定态薛定谔方程 的解又如何呢？
0 xa

2 2m
d
23 (x)
dx2

E3
( x),
xa
令：
k
2

2mE 2
k12

2m(V0 2
E)
三个区间的薛定谔方程化为：
V
V0
d
21(
dx2
x)

k
21
(
x)
空气隙
样品 STM工作示意图
利用光学中的受抑全反射理论，研制 成功光子扫描隧道显微镜（PSTM)。 1989年提出成象技术。 它可用于不导电样品的观察。
STM样品必须具有一定程度的导电性； 在恒流工作模式下有时对表面某些沟 槽不能准确探测。任何一种技术都有 其局限性。
讨论
从一维无限深方势阱 理解有限深方势阱
k2

2mE h2
V (x)
ka n n 1,2,3,
o
En

2 2
2ma 2
n2
n 1,2,3,
V (x) 0,
V (x) ,
ax
0 xa x 0, x a
E1

h2 2
2ma2

1 2
h2 2
ma2
,
微观能量尺度可以选取 h2 2
§2.4 一维方势阱
➢ 一维方势阱
E<U0
U0 V (x)
-a/2 a/2 x
对于参考书p47页说明
a)不在讨论为什么势能对称，波函数也对称了。 b) 公式29和30实质上是利用
c) 估计一下公式32的数值大小？ d)纵轴取决于势阱高度，横轴取决于能量，此处
是势阱内部动能。我们让动能变化，看看什 么时候能冲破势阱束缚。
因为隧道电流对针尖与样品间的距离十分敏感。 若控制针尖高度不变，通过隧道电流的变化可 得到表面态密度的分布；
利用STM可以分辨表面上 原子的台阶、平台和原子 探针 阵列。可以直接绘出表面
的三维图象
使人类第一次能够实时地观 测到单个原子在物质表面上 的排列状态以及与表面电子 行为有关的性质。在表面科 学、材料科学和生命科学等 领域中有着重大的意义和广 阔的应用前景。

0,
x0
I
d
2 3 (
dx2
x)

k
23
(
x)

0,
xa
II
III
oa x
d
22 (
dx2
x)

k12
2
(
x)

0,
0 xa
若考虑粒子是从 I 区入射，在 I 区中有入射波
反射波；粒子从I区经过II区穿过势垒到III 区，
在III区只有透射波。粒子在 x 0 处的几率要大
于在 x a 处出现的几率。
|xa
d3 ( x)
dx
|xa
求出解的形式画于图中。
定义粒子穿过势垒的贯穿系数：
P | 3(a) |2 | 1(0) |2
隧道效应
V
V0
P

| 2(a) |2 | 2 (0) |2

T exp(2k1a) T exp(2k10)
I
I(2k1a)

§2.4 一维方势阱
b)奇宇称 波函数为sin(kx)
结论:当
时才有解(见下一页图)
一维方势阱奇宇称能谱图
一维方势阱
c)当势场趋于无穷时,回到一维无限深势阱的特例
波函数的确定以及在非经典区间 内的衰减
衰减与动能有 关，动能越大 ，衰减越慢。
P47，公式29确定了A与D的关系，则公式 28所对应的全空间波函数仅有一个未定常 数，在全空间分段求函数的归一化，则可 以确定这个常数。至此，波函数与能量全 部确定。
其解为： 1(x) Aeikx Re ikx,
x0
2 (x) Tek1x , 0 x a
根据边界条件： 3(x) Ceikx, x a
1(0) 2 (0)
d1(x)
dx
|x0
d2 (x)
dx
|x0
2(a) 3(a)
d2 (x)
dx
ma2
微观动量尺度
ka = n
En

En1

En

h2 2 (2n 1)
2ma2
n1

1.5
h2 2
ma2

3 8
h2 2
m

a 2
2

因此，如果是微观粒子，m,a很小，E1也很小，使用相对 尺度来测量能量，而不是用绝对的能量单位来表达，
更直观。
一维方势阱
势阱外部 势阱内部
公式右面=
U0 2h2

U0
2h2
2
2
=
U0
=某个常数
2 2h2
ma2

ma2


2

ma2

微观能量尺度 h2 2
ma2
一维方势阱偶宇称能谱图
正确读图方法: 1、只留一条圆，因 为该圆半径由 势能高度决定。 2、一条圆与各周期 函数的交点，自左至 右，对应能级个数， 对应能级升高。 3、当半径很大时， 低能级交点首先pai/2 线，也就是趋近无穷 深势阱，为什么？
只要将原子线度的极细探针 以及被研究物质的表面作为 两个电极，当样品与针尖的 距离非常接近时，它们的表 面电子云就可能重叠。
若在样品与针尖之间 加一微小电压Ub电子 就会穿过电极间的势 垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。 若控制隧道电流不变，则探针在垂直于样品 方向上的高度变化就能反映样品表面的起伏。
exp(
2a
2m(V0 E))
当V0 E 5eV 时，势垒的宽度约50nm 以上时， 贯穿系数会小六个数量级以上。隧道效应在
实际上已经没有意义了。量子概念过渡到经典了。
• 隧道效应和扫描隧道显微镜STM Scanning tunneling microscopy
由于电子的隧道效应，金属中的电子并不完全局限于 表面边界之内，电子密度并不在表面边界处突变为零， 而是在表面以外呈指数形式衰减，衰减长度越为1nm。
具有不同的深度 但是宽度相同的方势阱(2)
势垒贯穿（隧道效应）
V
V (x) 0, x 0, x a
V0
V (x) V0 ,
0 xa
在经典力学中,若E V0 ,粒子的动能
为正,,它只能在 I 区中运动。
I II III
Oa x

2 2m
d
21 ( x)
dx2

E1 ( x),