求二面角的平面角

图1二面角计算一 、直接法：即先作出二面角的平面角，再利用解三角形知识求解之。

通常作二面角的平面角的途径有：⑴定义法：在二面角的棱上取一个特殊点，由此点出发在二面角的两个面内分别作棱的垂线；⑵三垂线法：如图1，C 是二面角βα--AB 的面β内的一个点，CO ⊥平面α于O ，只需作OD⊥AB 于D ，连接CD ，用三垂线定理可证明∠CDO 就是 所求二面角的平面角。

⑶垂面法：即在二面角的棱上取一点，过此点作平面γ，使γ垂直于二面角的棱，则γ 与二面角的两个面的交线所成的角就是该二面角的平面角。

例1 如图2，在四棱锥V-ABCD 中，底面ABCD 是正方形，侧面VAD 是正三角形, 平面VAD⊥底面ABCD ． （1）证明AB⊥平面VAD ；（2）求面VAD 与面VDB 所成的二面角的大小． 解：（1）证明：VAD ABCD AB AD AB VADAB ABCD AD VAD ABCD ⊥⎫⎪⊥⎪⇒⊥⎬⊂⎪⎪=⎭平面平面平面平面平面平面 （2）解：取VD 的中点E ，连结AF ，BE ， ∵△VAD 是正三形，四边形ABCD 为正方形， ∴由勾股定理可知，BD VB,===∴AE⊥VD，BE⊥VD，∴∠AEB 就是所求二面角的平面角. 又在Rt△ABE 中，∠BAE=90°，AB ，因此，tan∠AEB=.332=AE AB 即得所求二面角的大小为.332arctan例2 如图3，AB⊥平面BCD ，DC⊥CB，AD 与平面BCD成30°的角，且AB=BC.（1）求AD 与平面ABC 所成的角的大小； （2）求二面角C-AD-B 的大小；（3）若AB=2，求点B 到平面ACD 的距离。

解：(1) ∵AB⊥平面BCD ，∴∠ADB 就是AD 与平面BCD 所成的角,即∠ADB=300,且CD⊥AB， 又∵DC⊥BC，ABBC B =,∴ CD⊥平面ABC ，∴ AD 与平面ABC 所成的角为∠DAC ，设AB=BC=a,则AC=a 2， BD=acot300=a 3,AD=2a, a BC BD CD 222=-=,∴ tan∠DAC=122==aa CDAC , ∴ 045=∠DAC ,即，AD 与平面ABC 所成的角为450. (2)作CE⊥BD 于E ，取AD 的中点F ，连CF ， ∵ AB⊥面BCD ，ABD AB ⊂面， ∴ 面ABD⊥面BCD ， 又∵ 面ABD面BCD=BD ，BCD CE ⊂面，CE⊥BD，∴ CE⊥面ABD ，又∵AC=BC=a 2，AF=FD ，∴AD⊥EF，有三垂线定理的逆定理可知，∠CFE 就是所求二面角的平面角.计算可知, BC CD CE BD ⋅=，2AD a,=12CF AD a ==，∴ CE sin CFE CF ∠==故，所求的二面角为3.略例3如图4，P 是边长为1的正六边形ABCDEF 所在平面外一点，1PA =，P 在平面ABC 内的射影为BF 的中点O.（1）证明PA ⊥BF ；（2）求面APB 与面DPB 所成二面角的大小。

完整版)找二面角的平面角的方法汇总二面角是高中立体几何中的重要内容，但很多学生在解决二面角问题时往往无从下手，因为他们没有掌握寻找二面角的平面角的方法。

本文将介绍六种寻找二面角平面角的方法。

一、根据平面角的定义找出二面角的平面角。

例如，在60度的二面角α-a-β的两个面内，有点A和B，已知A和B到棱的距离分别为2和4，线段AB为10，求直线AB与棱a所构成的角的正弦值以及直线AB与平面α所构成的角的正弦值。

为解决这道题，需要先找到二面角的平面角，即找到60度角所在的位置。

根据题意，在平面β内作AD垂直于a，在平面α内作BE垂直于α，CD平行于EB，然后连接BC、AC。

可以证明CD垂直于a，因此根据二面角平面角的定义，∠ADC为二面角α-a-β的平面角。

二、根据三垂线定理找出二面角的平面角。

例如，在平面β内有一条直线AC与平面α成30度，AC与棱BD成45度，求平面α与平面β的二面角的大小。

为了寻找二面角的平面角，可以通过点A作AF垂直于BD，AE垂直于平面α，并连接FE。

根据三垂线定理，可以证明BD垂直于EF，因此∠AFE 为二面角的平面角。

需要注意的是，寻找二面角平面角时需要注意“作”、“连”、“证”的顺序。

三、作二面角棱的垂面，垂面与二面角的两个面的两条交线所构成的角，即为二面角的平面角。

例如，在图1中，已知P为α-CD-β内的一点，PA垂直于α于点A，PB垂直于β于点B，如果∠APB=n度，则需要求二面角α-CD-β的平面角。

由PA垂直于α和PB垂直于β可得CD垂直于平面PAB。

因此，只需要画出平面PAB与平面α、β的交线即可。

可以证明∠AEB为α-CD-β的平面角，且∠AEB=180-n度（如图2）。

需要注意的是，如果通过点A作AE垂直于CD，垂足为E，并连接EB，则还需要证明EB垂直于CD，以及AEBP为平面图形。

由于篇幅限制，本文只介绍了三种寻找二面角平面角的方法，其他三种方法包括作二面角棱的垂线，作二面角的高线，以及利用向量的方法。

求二面角的平面角的九种方法
李永茂;刘文春
【期刊名称】《数学教学》
【年(卷),期】1990(000)006
【摘要】在立体几何中解二面角的问题,关键是正确地作出其平面角.以下给出九种常用的方法. （一）观察法. 当两半平面的位置关系较明显时,可用该方法. 例一.如图1.棱长为1的正方体AC₁.
【总页数】3页(P28-30)
【作者】李永茂;刘文春
【作者单位】[1]天津静海县教研室;[2]天津静海县唐官屯中学
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.“一线法”求二面角的平面角 [J], 吕井奎
2.求二面角的平面角方法列举 [J], 戴立
3.确定二面角的平面角的一种方法 [J], 卢剑春
4.夹垂线（面）法求作二面角的平面角 [J], 王常庆
5.向量的叉乘在立体几何求二面角平面角大小中的应用 [J], 程振
因版权原因，仅展示原文概要，查看原文内容请购买。

求解二面角的六种常规方法作者：李淑芸来源：《中学教学参考·理科版》2010年第03期求解二面角问题是高考的热点问题,在近几年的高考中几乎每一年、每一套高考题的立体几何问题都涉及到求二面角的大小问题.然而通过对学生考卷的分析,我们发现这一问题的得分率却并不理想.因此,本文总结了常见的六种求解二面角的方法,希望能给部分读者以帮助.1.定义法是指过二面角的棱上任一点在两个面内分别作垂直于棱的直线,则两直线所构成的角即为二面角的平面角,继而在平面中求出其平面角的一种方法.【例1】如图1,空间四边形ABCD中,AB=BC=CD=DA=a,对角线AC=a,BD=2a,求二面角A—BD—C的大小.图1解:取BD的中点为O,分别连接AO、CO,∵AB=AD,BC=CD.∴AO⊥BD,CO⊥BD.∴∠AOC为二面角A—BD—C的平面角.∵AB=AD=a,BD=2a,∴AO=22a.∵BC=CD=a,BD=2a,∴OC=22a.在△AOC中,OC=22a,OA=22a,AC=a,OA2+OC2=AC2,∴∠AOC=90°,即二面角A—BD—C为直二面角.2三垂线法是指利用三垂线定理,根据“与射影垂直,则也与斜线垂直”的思想构造出二面角的平面角,继而求出平面角的方法.【例2】如图2,二面角α-AB-β的棱AB上有一点C,线段CDα,CD=100,∠BCD=30°,点D 到平面β的距离为253,求二面角α-AB-β的度数.图2解:过D作DE⊥β于E,DF⊥AB于F,连接EF.∵DF⊥AB,EF是DF在β内的射影,∴AB⊥EF(三垂线定理).∴∠DFE为二面角为α-AB-β的平面角.在Rt△DEF中,DF=12CD=50,DE=253,∴sin∠DFE=DEDF=25350=32.∴∠DFE=60°.即二面角α-AB-β的度数为60°.3.垂面法是指用垂直于棱的平面去截二面角,则截面与二面角的两个面必有两条交线,这两条交线构成的角即为二面角的平面角,继而再求出其平面角的一种方法.【例3】如图3,已知SA⊥平面ABC,AB⊥BC,SA=AB,SB=BC,E是SC的中点,DE⊥SC交AC于D,求二面角E-BD-C的大小.图3解:∵BS=BC,SE=EC,∴SC⊥BE,又∵SC⊥DE,∴SC⊥面BDE.∴SC⊥BD.又∵BD⊥SA,∴BD⊥面SAC.∴∠EDC为二面角E-BD-C的平面角.设SA=a,则SB=BC=2a.∵BC⊥AB,SA⊥平面ABC.∴BC⊥SB.∴SC=2a,∠SCD=30°.∴∠EDC=60°,即二面角E-BD-C的大小为60°.4.面积射影法所谓面积射影法,就是根据三角形及其在某一个平面上的射影面积之间的关系,利用cosθ=S射S来计算二面角的一种方法(其中θ为二面角).【例4】在正方体ABCD-A1B1C1D1中,K∈BB1,M∈CC1,且BK=14BB1,CM=34CC1,求平面AKM与ABCD所成角的大小.图4解:连结AC,则由题意可知,△ABC是△AKM在平面AC上的射影.设平面AKM与ABCD所成角为θ,则cosθ=S射S=S△ABCS△AKM.令正方体的棱长为4,∴S△ABC=12AB•A C=12×4×4=8.在△AKM中,AK=12+42=17,AM=42+42+32=41,KM=42+22=20.由海伦公式可知S△AKM=221,∴cosθ=421,θ=arccos421.5.法向量法法向量法是通过求与二面角垂直的两个向量所成的角,继而利用这个角与二面角的平面角相等或互补的关系,求出二面角的一种方法.【例5】如图5,过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=ɑ,求平面PAB 和平面PCD所成的二面角的大小.图5解:以A为射点建立直角坐标系(如图5所示),则P(0,0,a),D(0,a,0),C(a,a,0).设平面PCD的法向量为n=(x,y,z),则n•PD=0,n•CD=0.即(x,y,z)•(0,a,-a)=0,(x,y,z)•(-a,0,0)=0.∴y=-z,x=0.即n=(0,1,-1).又AD成为平面PAB的法向量,而cos〈AD,n〉=(0,a,0)•(0,1,-1)a•2=22,∴AD与n所成的角为45°.因此平面PAB和平面PCD所成的角为45°.6.垂线法是指先利用待定系数法确定垂足,再利用公式求出二面角的大小.【例6】如图6,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC,已知PD=2,CD=2,AE=12,求(1)异面直线PD与EC的距离;(2)二面角E-PC-D的大小.图6解:(1)略.(2)以D为原点,DA、DC、DP分别为x,y,z轴建立空间直角坐标系.作DG⊥PC,可设G(0,y,z).由DG•PC=0得(0,y,z)•(0,2,-2)=0,即z=2y.故可取DG=(0,1,2).作EF⊥PC于F,设F(0,m,n),则EF=(-32,m-12,n).由EF•PC=0,得(-32,m-12,n)•(0,2,-2)=0,即2m-1-2n=0.又由F在PC上得n=-22m+2,故m=1,n=22,EF=(-32,12,22).因EF⊥PC,DG⊥PC,故二面角E-PC-D的平面角θ的大小为向量EF与DG的夹角.故cosθ=DG•EF|DG|•|EF|=22,∴θ=π4.故二面角E-PC-D的大小为π4.(责任编辑金铃)。

二面角基本求法一、基本观点(一).求二面角的主要方法：（1） 定义法：①找（作）二面角的平面角；【先证】②解三角形求出角。

【后算】 （2） 公式法：设二面角的度数为θ，则侧面三角形射影三角形S S =θcos多用于求无棱二面角。

(二) 求作二面角的平面角求作二面的平面角是解决二面角问题的关键，也是难点，通过前面教学及习题涉及到的作法有下面三种：1.定义法2.三垂线法：3.垂面法二.求二面角的大小的基本方法为先证后算,即先由有关立几结论找出二面角的平面角(大多数题是用三垂线法去找),然后借助于解三角形求出平面角. 例题解析一.定义法：从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面，在棱上取点，分别在两面内引两条射线与棱垂直，这两条垂线所成的角的大小就是二面角的平面角。

[例1].如图 在三棱锥S —ABC 中，∠SAB =∠SAC =∠ACB =90°，且AC =BC =5，SB =55（Ⅰ）证明：SC ⊥BC ；（Ⅱ）求侧面SBC 与底面ABC 所成二面角的大小；变式1：在正三角形ABC 中，AD ⊥BC 于D ，沿AD 折成二面角B-AD-C 后，BC=21AB ，求二面角B-AD-C 的大小。

变式2: 设P 是二面角α－l －β内一点，P 到面α、β的距离PA 、PB 分别为8和5，且AB＝7，求这个二面角的大小。

.[例2]如图所示,已知四棱锥S--ABCD 的底面ABCD 是正方形，SA ⊥底面ABCD ，点E 是SC 上任意一点.（Ⅰ）求证：平面EBD ⊥平面SAC ；（Ⅱ）设SA=4，AB=2，求点A 到平面SBD 的距离；（Ⅲ）当SAAB的值为多少时，二面角B-SC-D 的大小为120°。

二、三垂线法三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。

★二面角的平面角的求法：⒈定义法：在二面角的棱上找一点（特殊点），在两个半平面内分别作垂直与棱的射线。

如图，在二面角βα--a 的棱a 上任取一点O ，在平面α内过点O 作a OA ⊥，在平面β内过点O 作a BO ⊥，则AOB ∠为二面角βα--a 的平面角。

⒉垂面法：过棱上一点作棱的垂直平面，该平面与二面角的两个半平面产生交线，这两条射线所成的角，即为二面角的平面角。

如图，已知二面角-αβ-l ，过棱上一点O 作一平面γ，使l γ⊥，.,OB OA =⋂=⋂βγβγOB l OA l OB OA ⊥⊥⊆⊆,,,γγ ∴ AOB ∠为二面角βα--l 的平面角。

⒊垂线法：※ 该法也就是利用三垂线定理或逆定理来寻找二面角的平面角，是最常用的一种方法。

由一个半平面内异与棱上的点A 向另一个半平面作垂线，垂足为B ，由点B 向二面角的棱作垂线，垂足为O ，连结AO ，则AOB ∠为二面角的平面角。

如图，已知二面角βα--l ，自平面α内一点A 作AB β⊥于B ，由点B 作BO l ⊥于O ，连结AOAO 为平面β的斜线，BO 为AO 在平面β内的射影∴ AO ,l ⊥∴ AOB ∠为二面角l -α-β的平面角。

⒋射影法： 被投影面投影面S S =θcos⒌向量法：（1）⑴AB,CD 分别是二面角βα--l 的两个面内与棱AC 垂直的异面直线，则二面角的大小为CD AB .[（2）平面α与β相交于直线l ，平面α的法向量为n 1，平面β的法向量为n 2，<n 1，n 2>＝θ，则二面角α－l －β为θ或π－θ.设二面角大小为φ，则|cos φ|＝|cos θ|＝|n 1·n 2||n 1|·|n 2|. ★★利用二面角的两个面的法向量求解※ 法向量的夹角与二面角的大小相等或互补①当法向量21n n 与的方向分别指向二面角的内侧与外侧时，二面角的大小等于法向量夹角②当法向量1n 与2n 方向同时指向二面角的内侧或外侧时，二面角的大小等于法向量夹角的补角，1．二面角的棱上有A 、B 两点，直线AC 、BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知AB ＝4，AC ＝6，BD ＝8，CD ＝217，则该二面角的大小为( )A ．150°B ．45°C ．60°D ．1202.如图，四棱锥S -ABCD 的底面是边长为1的正方形，SD ⊥底面ABCD ，SB ＝3，求平面ASD 与平面BSC 所成二面角的大小．3.如图，在四棱锥P－ABCD中，底面ABCD是矩形，P A⊥平面ABCD，AP＝AB＝2，BC＝22，E，F分别是AD，PC的中点．(1)证明：PC⊥平面BEF.(2)求平面BEF与平面BAP夹角的大小．4.如图，在长方体ABCD—A1B1C1D1中，E、F分别是棱BC，CC1上的点，CF＝AB＝2CE，AB∶AD∶AA1＝1∶2∶4.(1)求异面直线EF与A1D所成角的余弦值；(2)证明AF⊥平面A1ED；(3)求二面角A1-ED-F的正弦值．5.如图所示，在正三棱柱ABC－A1B1C1中，底面边长为a，侧棱长为22a，D是棱A1C1的中点．(1)求证：BC1∥平面AB1D；(2)求二面角A1－AB1－D的大小；6．(12分)在直三棱柱ABC-A1B1C1中，AB＝AC＝1，∠BAC＝90°且异面直线A1B与B1C1所成的角等于60°，设AA1＝a.(1)求a的值；(2)求平面A1BC1与平面B1BC1所成的锐二面角的大小．7.．如图，已知正方形ABCD 和梯形ACEF 所在平面互相垂直，AB ＝2，AF ＝22，CF ∥AF ，AC ⊥CE ，ME →＝2FM →，(1)求证：CM ∥平面BDF ；(2)求异面直线CM 与FD 所成角的余弦值的大小；(3)求二面角A －DF －B 的大小．8. (2010·湖北)如图所示，在四面体A －BOC 中，OC ⊥OA ，OC⊥OB ，∠AOB ＝120°，且OA ＝OB ＝OC ＝1.(1)设P 为AC 的中点，证明：在AB 上存在一点Q ，使PQ ⊥OA ，并计算AB AQ的值； (2)求二面角O -AC -B 的平面角的余弦值．9．(14分)已知四棱锥S -ABCD 的底面ABCD 是正方形，SA ⊥底面ABCD ，E 是SC 上的任意一点．(1)求证：平面EBD ⊥平面SAC ；(2)当SA AB的值为多少时，二面角B -SC -D 的大小为120°.。

C A B DA A 1B DC C 1 B 1 解二面角问题（一）寻找有棱二面角的平面角的方法和求解。

（1）定义法：利用二面角的平面角的定义，在二面角的棱上取一点，过该点在两个半平面内作垂直于棱的射线，两射线所成的角就是二面角的平面角，这是一种最基本的方法。

要注意用二面角的平面角定义的三个“主要特征”来找出平面角，当然这种找出的角要有利于解决问题。

下面举几个例子来说明。

例1：如图，立体图形V －ABC 的四个面是全等的正三角形，画出二面角V －AB －C 的平面角并求出它的度数。

例2：在三棱锥P-ABC 中，∠APB=∠BPC=∠CPA=600，求二面角A-PB-C 的余弦值。

这样的类型是不少的，如下列几道就是利用定义法找出来的：1、在正方体ABCD －A 1B 1C 1D 1中，找出二面角B －AC －B 1的平面角并求出它的度数。

2、．边长为a 的菱形ABCD ，∠ACB=600，现沿对角线BD 将其折成才600的二面角，则A 、C 之间的距离为 。

（菱形两条对角线互相垂直，对折后的一条对角线成两条线段仍都垂直于另一条对角线，则所成的角是二面角的平面角）3、正三棱柱ABC —A 1B 1C 1的底面边长是4，过BC 的一个平面与AA 1交于D ，若AD =3，求二面角D ―BC ―A 的正切值。

总之，能用定义法来找二面角的平面角的，一般是图形的性质较好，能够较快地找到满足二面角的平面角的三个主要特征。

并且能够很快地利用图形的一些条件来求出所要求的。

在常见的几何体有正四面体，正三棱柱，正方体，以及一些平面图形，正三角形，等腰三角形，正方形，菱形等等，这些有较好的一些性质，可以通过它们的性质来找到二面角的平面角。

至于求角，通常是把这角放在一个三角形中去求解。

由图形及题目的已知条件来求这个三角形的边长或者角，再用解三角形的知识去求解。

（2）三垂线法：是利用三垂线的定理及其逆定理来证明线线垂直，来找到二面角的平面角的方法。

用公式法求二面角的平面角1.问题的提出大家知道，当一个三面角的三个面角都固定时，则它们任意两个面的平面角的大小也就确定．它们之间一定存在着某种必然的内在联系．事实上，我们有如下的定理．定理 设ABC O -为一个三面角，ϕ=∠AOB ，1θ=∠AOC ，2θ=∠BOC ，二面角B OC A --的平面角为α，则有αθθθθϕcos sin sin cos cos cos 2121+=．略证：如图，OC AC ⊥，OC BC ⊥，则α=∠A C B ．令a OA =，b OB =．在Rt △ACO 中，1sin θa AC =，1cos θa OC =．同理，2sin θb BC =，2cos θb OC =．故21cos cos θθb a =．又在△AOB 中，ϕcos 2222ab b a AB -+=， ①在△ABC 中，αθθθθcos sin sin 2sin sin 212221222ab b a AB -+=． ② 由①，②得αθθθθϕcos sin sin cos cos cos 2121+=．证毕同理可证，当1θ，2θ中有一个为钝角（或直角）时，公式也照样成立（这里从略）．由此可知：（1）将此公式反过来，只要知道了1θ，2θ，ϕ，即可求平面角α；（2）此公式与三角形中的余弦定理有相似之处，不妨把它叫做三面角的余弦定理．2.例题例 1 已知正三棱锥侧面与底面的夹角为α，任两侧面的夹角为β，求证01cos 2cos 32=-+βα．略证：如图2，设ABC V -为正棱锥，VAC B -构成三面角．又设C AB V --的平面角为α，C VB A --的平面角为β，ϕ=∠=∠VBC ABV ．由公式得:αϕϕϕcos 60sin sin 60cos cos cos +=，故αϕcos 3ctg =． ①又βϕϕcos sin cos 60cos 22+= ，故βϕcos 21ctg 2-=． ② 由①，②得 01cos 23cos 2=-+βα．例 2 如图，在梯形ABCD 中，BC AD //，a AB =，a AD 3=，a PA =，2π=∠ABC ，55arcsin =∠ADC ，⊥PA 平面ABCD ，求以CD 为棱的二面角A CD P --的大小（1994年上海高考题）．略解：APC D -构成三面角，令ϕ=∠PDA ，则a PA AD PD 1022=+=，a 10103cos =ϕ， 1θ=∠ADC ，55arcsin=∠ADC ，55sin 1=θ，552c 1=θos ． 由a AB =，a AD 3=，55arcsin =∠ADC ，知a BC =，a CD 5=． 又在Rt △PAB 中，由a PA =，a AB =，得a PB 2=． 在Rt △PBC 中，a PC 3=．令2θ=∠PDC ，则5232cos 2222=⋅⋅-+=PD CD PC PD CD θ，57sin 2=θ． 由公式得αcos 575552355210103⋅+⋅=，14143cos =α． ∴14143arccos =α． 例3 如图,已知正三棱柱ABC C B A -111，D 为AC 之中点，（1）求证：//1AB 平面1BDC ；（2）若11BC AB ⊥，求以1BC 为棱二面角C BC D --1的大小．（1994年高考题，本文公解（2））．略解：1-CDC B 为三面角，连结1BC ，交C B 1于E ．连结DE ．DBE BC DE BC AB BC AB DE ∆⇒⊥⊥==111112121，为等腰直角三角形．令a CA BC AB ===，则a DC BD 231==，a BC 261=． 由22212121a CD D C C C =-=，得a C C 221=．设 30=∠=CBD ϕ， 4511=∠=DBC θ，22cos sin 11==θθ，12CBC ∠=θ，36cos 2=θ，33sin 2=θ．由公式得αθθcos sin 45sin cos 45cos 30cos 22+= 即αcos 3322362223⋅+⋅=，22cos =α．∴ 45=α．。

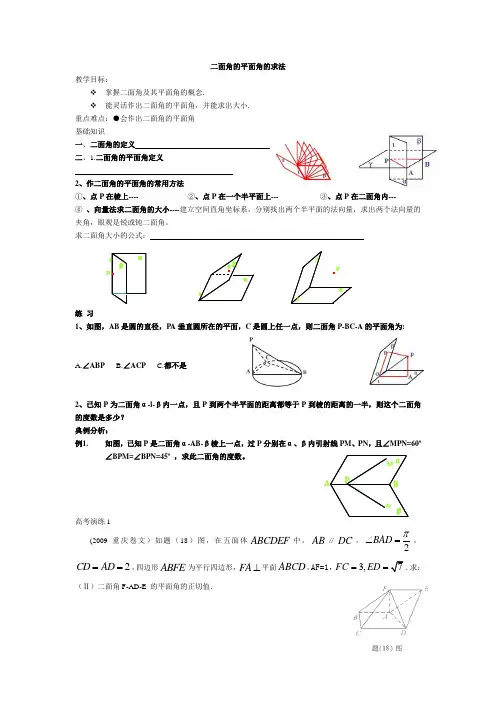
二面角的平面角的求法教学目标：掌握二面角及其平面角的概念.能灵活作出二面角的平面角，并能求出大小. 重点难点：●会作出二面角的平面角①、点P 在棱上---- ②、点P 在一个半平面上--- ③、点P 在二面角内--- ④ 、向量法求二面角的大小----建立空间直角坐标系，分别找出两个半平面的法向量，求出两个法向量的夹角，眼观是锐或钝二面角。

求二面角大小的公式： 练 习1、如图，AB 是圆的直径，PA 垂直圆所在的平面，C 是圆上任一点，则二面角P-BC-A 的平面角为:A.∠ABPB.∠ACPC.都不是2、已知P 为二面角α-l-β内一点，且P 到两个半平面的距离都等于P 到棱的距离的一半，则这个二面角的度数是多少？ 典例分析： 例1. 如图，已知P 是二面角α-AB-β棱上一点，过P 分别在α、β内引射线PM 、PN ，且∠MPN=60º ∠BPM=∠BPN=45º ，求此二面角的度数。

高考演练1(2009重庆卷文）如题（18）图，在五面体ABCDEF中，AB∥DC，2BAD π∠=，2CD AD ==，四边形ABFE 为平行四边形，FA ⊥平面ABCD ，AF=1，（Ⅱ）二面角F-AD-E 的平面角的正切值．例2．如图P 为二面角α–ι–β内一点，PA ⊥α,PB ⊥β,且PA=5， PB=8，AB=7，求这二面角的度数。

例3．如图，三棱锥P-ABC 的顶点P 在底面ABC 上的射影是底面Rt △ABC 斜边AC 的中点O ，若PB=AB=1，BC= ，求二面角P-AB-C 的正切值。

高考演练2（2009四川卷文）（本小题满分12分）如图，正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直，△是等腰直角三角形，,,45ABAE FA FEAEF ︒==∠=（III ）求二面角F BD A --的大小。

练习1：已知Rt △ABC 在平面α内，斜边AB 在30º的二面角α-AB-β的棱上，若AC=5，BC=12，求点C 到平面β的距离CO 。