高等数学D 空间直角坐标系

高数下册常用常见知识点高等数学下册常用知识点第八章：空间解析几何与向量代数一、向量及其线性运算1.向量的概念及基本性质：包括向量相等、单位向量、零向量、向量平行、共线、共面等基本概念。

2.向量的线性运算：包括加减法和数乘。

3.空间直角坐标系：包括坐标轴、坐标面、卦限和向量的坐标分解式等。

4.利用坐标进行向量的运算：设向量a=(ax。

ay。

az)，向量b=(bx。

by。

bz)，则a±b=(ax±bx。

ay±by。

az±bz)，λa=(λax。

λay。

λaz)。

5.向量的模、方向角、投影：包括向量的模、两点间的距离公式、方向角、方向余弦和投影等。

二、数量积和向量积1.数量积：包括数量积的概念、性质和计算公式等。

2.向量积：包括向量积的概念、性质和计算公式等。

三、曲面及其方程1.曲面方程的概念：包括曲面方程的定义和基本性质等。

2.旋转曲面：包括旋转曲面的定义、方程和旋转后方程的计算等。

3.柱面：包括柱面的特点、方程和母线的概念等。

4.二次曲面：包括椭圆锥面的方程和图形等。

2.椭球面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$3.旋转椭球面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$4.单叶双曲面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$5.双叶双曲面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1$6.椭圆抛物面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=z$7.双曲抛物面（马鞍面）：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=z$8.椭圆柱面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$9.双曲柱面：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$10.抛物柱面：$2x=ay^2$空间曲线及其方程：1.参数方程：$\begin{cases}x=x(t)\\y=y(t)\\z=z(t)\end{cases}$，如螺旋线：$\begin{cases}x=a\cos t\\y=a\sin t\\z=bt\end{cases}$2.一般方程：$F(x,y,z)=0$，消去$z$，得到曲线在面$xoy$上的投影。

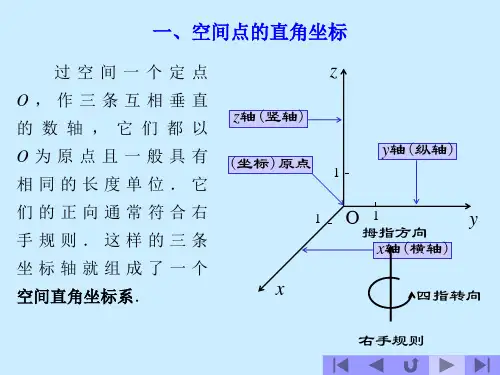
第七章向量代数与空间解析几何空间解析几何是多元函数微积分学必备的基础知识.本章首先建立空间直角坐标系，然后引进有广泛应用的向量代数，以它为工具，讨论空间的平面和直线，最后介绍空间曲面和空间曲线的部分内容.第一节空间直角坐标系平面解析几何是我们已经熟悉的，所谓解析几何就是用解析的，或者说是代数的方法来研究几何问题.坐标法把代数与几何结合起来.代数运算的基本对象是数,几何图形的基本元素是点.正如我们在平面解析几何中所见到的那样，通过建立平面直角坐标系使几何中的点与代数的有序数之间建立一一对应关系.在此基础上,引入运动的观点,使平面曲线和方程对应,从而使我们能够运用代数方法去研究几何问题.同样,要运用代数的方法去研究空间的图形——曲面和空间曲线,就必须建立空间内点与数组之间的对应关系.一、空间直角坐标系空间直角坐标系是平面直角坐标系的推广.过空间一定点O，作三条两两互相垂直的数轴，它们都以O为原点.这三条数轴分别叫做x轴（横轴）、y轴（纵轴）、z轴（竖轴），统称坐标轴.它们的正方向按右手法则确定，即以右手握住z轴，右手的四个手指指向x轴的正向以π2角度转向y轴的正向时，大拇指的指向就是z轴的正向（图7-1），这样的三条坐标轴就组成了一空间直角坐标系Oxyz，点O叫做坐标原点.图7-1三条坐标轴两两分别确定一个平面，这样定出的三个相互垂直的平面:xOy,yOz,zOx,统称为坐标面.三个坐标面把空间分成八个部分，称为八个卦限，上半空间（z＞0）中，从含有x 轴、y轴、z轴正半轴的那个卦限数起，按逆时针方向分别叫做Ⅰ，Ⅱ，Ⅲ，Ⅳ卦限，下半空间（z＜0）中，与Ⅰ，Ⅱ，Ⅲ，Ⅳ四个卦限依次对应地叫做Ⅴ，Ⅵ，Ⅶ，Ⅷ卦限（图7-2）.图7-2确定了空间直角坐标系后，就可以建立起空间点与数组之间的对应关系.设M为空间的一点，过点M作三个平面分别垂直于三条坐标轴，它们与x轴、y轴、z 轴的交点依次为P、Q、R（图7-3）.这三点在x轴、y轴、z轴上的坐标依次为x，y，z.这样，空间的一点M就惟一地确定了一个有序数组（x，y，z），它称为点M的直角坐标，并依次把x,y和z叫做点M的横坐标，纵坐标和竖坐标.坐标为（x,y,z）的点M通常记为M（x,y,z）.图7-3反过来，给定了一有序数组（x,y,z），我们可以在x轴上取坐标为x的点P，在y轴上取坐标为y的点Q，在z轴上取坐标为z的点R，然后通过P、Q与R分别作x轴，y轴与z 轴的垂直平面，这三个平面的交点M就是具有坐标（x,y,z）的点（图7-3）.从而对应于一有序数组（x,y,z），必有空间的一个确定的点M.这样，就建立了空间的点M和有序数组（x,y,z）之间的一一对应关系.如图7-3所示x轴，y轴和z轴上的点的坐标分别为P（x,0,0），Q（0,y,0）,R（0,0,z）；xOy面，yOz面和zOx面上的点的坐标分别为A（x,y,0），B（0，y,z）,C（x,0,z）；坐标原点O的坐标为O（0,0,0）.它们各具有一定的特征，应注意区分.二、空间两点间的距离设M1（x1,y1,z1）、M2（x2,y2,z2）为空间两点，为了用两点的坐标来表达它们间的距离d，我们过M1，M2各作三个分别垂直于三条坐标轴的平面.这六个平面围成一个以M1，M2为对角线的长方体（图7-4）.根据勾股定理，有图7-4｜M 1M 2｜2＝｜M 1N ｜2＋｜NM 2｜2＝｜M 1P ｜2＋｜M 1Q ｜2＋｜M 1R ｜2.由于｜M 1P ｜＝｜P 1P 2｜＝｜x 2－x 1｜,｜M 1Q ｜＝｜Q 1Q 2｜＝｜y 2－y 1｜,｜M 1R ｜＝｜R 1R 2｜＝｜z 2－z 1｜,所以d ＝｜M 1M 2｜＝212212212)()()(z z y y x x -+-+-，这就是两点间的距离公式.特别地，点M （x,y,z ）与坐标原点O （0,0,0）的距离为d ＝｜OM ｜＝222z y x ++。

大学高等数学知识点框架
一、微积分
1.导数与微分
2.积分与不定积分
3.定积分与曲线下面积
4.微分方程
二、级数
1.数列与级数的概念
2.收敛与发散
3.数项级数
4.幂级数
三、微分方程
1.一阶微分方程
2.二阶线性齐次微分方程
3.二阶线性非齐次微分方程
4.变量分离法与齐次微分方程
四、空间解析几何
1.三维空间直角坐标系
2.平面与直线的方程
3.空间曲面与二次曲线
4.空间直线与平面的位置关系
五、多元函数微分学
1.多元函数的极限
2.偏导数与全微分
3.多元复合函数的求导法则
4.隐函数与参数方程的求导
六、重积分与曲线曲面积分
1.重积分的概念与性质
2.二重积分的计算
3.三重积分的计算
4.曲线曲面积分的计算
七、常微分方程
1.一阶常微分方程
2.二阶常微分方程
3.高阶常微分方程
4.常微分方程的解析解与数值解
八、线性代数
1.线性方程组与矩阵
2.矩阵的运算与性质
3.矩阵的秩与逆
4.特征值与特征向量
九、概率论与数理统计
1.基本概念与概率空间
2.随机变量及其分布律
3.多维随机变量与联合分布
4.参数估计与假设检验
以上是大学高等数学的主要知识点框架，涵盖了微积分、级数、微分方程、空间解析几何、多元函数微分学、重积分与曲线曲面积分、常微分方程、线性代数以及概率论与数理统计等内容。

通过深入学习这些知识点，可以建立起扎实的数学基础，为进一步学习相关学科打下坚实的基础。

大一空间解析几何知识点总结大一空间解析几何是大学数学的一门基础课程，主要研究几何对象在空间中的性质和相互关系。

以下是大一空间解析几何的一些主要知识点总结，供参考学习：1. 空间直角坐标系：空间直角坐标系是三维空间中最常用的坐标系，它由三条相互垂直的坐标轴构成，通常用x、y、z表示。

空间中的点可以由它们在三个坐标轴上的坐标表示。

2. 点的坐标计算：在空间直角坐标系中，给定一个点P，可以通过测量与三个坐标轴的距离，计算出点P的坐标。

例如，点P在x轴上的坐标为x，点P在y轴上的坐标为y，点P在z轴上的坐标为z。

3. 点、线、面的方程：通过坐标计算，可以得到点、线、面的方程。

例如，对于点P(x, y, z)，点P的坐标就可以通过方程x = x，y = y，z = z来表示。

对于直线l，可以通过两点的坐标计算直线的方程。

对于平面，可以通过三点的坐标计算平面的方程。

4. 空间中的距离：空间中两点之间的距离可以通过勾股定理计算。

设点P(x1, y1, z1)和点Q(x2, y2, z2)为两点，它们之间的距离为d，表示为d = √[(x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2]。

5. 点、线的位置关系：在空间解析几何中，点和线的位置关系有几种情况：点在直线上、点在直线外、点在直线的延长线上等。

可以通过点和线的坐标来判断它们的位置关系。

6. 直线的方向向量和参数方程：在空间直角坐标系中，直线可以用方程式表示，其中的参数t表示直线上的任意一点P的位置。

直线的方向向量可以用一个行向量表示，例如，直线l可以表示为l：(x, y, z) = (x0, y0, z0) + t(a, b, c)，其中，(x0, y0, z0)表示直线上一点，(a, b, c)表示直线的方向向量。

7. 平面的法向量和一般方程：在空间直角坐标系中，平面可以用方程式表示。

平面的一般方程为Ax + By + Cz + D = 0，其中(A, B, C)为平面的法向量，D为常数。

高等数学下册第七章习题答案详解1. 在空间直角坐标系中，定出下列各点的位置：()123A ，，；()2,3,4B -； 2,3,4C --（）； D 3,4,0（）；()0,4,3E ；3,0,0F （）. 解：点A 在第Ⅰ卦限；点B 在第Ⅱ卦限；点C 在第Ⅷ卦限； 点D 在xOy 面上；点E 在yOz 面上；点F 在x 轴上.2. xOy 坐标面上的点的坐标有什么特点？yOz 面上的呢？zOx 面上的呢？ 答: 在xOy 面上的点，z =0;在yOz 面上的点，x =0; 在zOx 面上的点，y =0.3. 对于x 轴上的点，其坐标有什么特点?y 轴上的点呢?z 轴上的点呢? 答：x 轴上的点，y =z =0;y 轴上的点，x =z =0; z 轴上的点，x =y =0.4. 求下列各对点之间的距离： (1) (000)，，，(234)，，； (2) (000)，，，(23,4)--，； (3) (2,3,4)--，() 1,0,3； (4) (4,2,3)-，(2,1,3)-.解：（1）22223429s =++=(2) 2222(3)(4)29s =+-+-=(3) 222(12)(03)(34)67s =++-++=(4) 222(24)(12)(33)35s =--+++-=5. 求点(4,3,5)-到坐标原点和各坐标轴间的距离.解：点(4，-3，5)到x 轴，y 轴，z 轴的垂足分别为（4，0，0），（0，-3，0），（0，0，5）. 故 22204(3)552s =+-+=222(44)(30)(50)34x s =-+--+-=2224(33)541y s =+-++=2224(3)(55)5z s =+-+-=.6. 在z 轴上求一点，使该点与两点(4,1,7)A -和(3,5,2)B -等距离. 解：设此点为M （0，0，z ），则222222(4)1(7)35(2)z z -++-=++--解得 149z =即所求点为M （0，0，149）. 7. 试证:以三点(4,1,9)A ，(10,1,6)B -，(2,4,3)C 为顶点的三角形是等腰直角三角形. 证明：因为|AB |=|AC |=7.且有 |AC |2+|AB |2=49+49=98=|BC |2. 故△ABC 为等腰直角三角形.习题7-21. 验证:()()++=++a b c a b c . 证明：利用三角形法则得证.见图7-1图12. 设2,3=-+=-+-u a b c v a b c .试用a,b,c 表示23-u v . 解：232(2)3(3)2243935117-=-+--+-=-++-+=-+u v a b c a b c a b c a b c a b c3.把ABC ∆的BC 边五等分，设分点依次为1234,,,D D D D ，再把各分点与A 连接，试以,AB BC ==c a 表示向量123,,A D A D A D 和4D A .解：1115D A BA BD =-=--c a 2225D A BA BD =-=--c a3335D A BA BD =-=--c a444.5D A BA BD =-=--c a4. 设向量OM 的模是4，它与投影轴的夹角是60°，求这向量在该轴上的投影. 解：设M 的投影为M '，则1Pr j cos604 2.2u OM OM =︒=⨯=5. 一向量的终点为点(2,1,7)B -，它在三坐标轴上的投影依次是4，－4和7，求这向量的起点A 的坐标.解：设此向量的起点A 的坐标A (x , y , z )，则{4,4,7}{2,1,7}AB x y z =-=----解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0). 6. 一向量的起点是1(4,0,5)P ，终点是2(7,1,3)P ，试求: (1) 12P P 在各坐标轴上的投影； (2) 12P P 的模；(3) 12P P 的方向余弦； (4) 12P P 方向的单位向量.解：（1）12Pr j 3,x x a PP == 12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==- (2) 22212(74)(10)(35)14PP =-+-+-=(3) 123cos 14x a PP α==121cos 14y a PP β==122cos 14z a PP γ-==(4) 120123{}141414141414PP PP ===-e j . 7. 三个力123(1,2,3),(2,3,4),(3,4,5)=---F F F 同时作用于一点，求合力R 的大小和方向余弦. 解：R =（1-2+3，2+3-4，3-4+5）=（2，1，4）222||21421=++=R cos cos cos 212121αβγ=== 8. 求出向量,235=++=-+a i j k b i j k 和22=--+c i j k 的模，并分别用单位向量,,a b c e e e 来表达向量,,a b c .解：222||1113=++=a222||2(3)538=+-+=b222||(2)(1)23=-+-+=c3, 38, 3. a b c ===a e b e c e9. 设358,247,54,=++=--=+-m i j k n i j k p i j k 求向量43=+-a m n p 在x 轴上的投影及在y 轴上的分向量.解：a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k 在x 轴上的投影a x =13,在y 轴上分向量为7j . 10. 已知单位向量a 与x 轴正向夹角为π3，与其在xOy 平面上的投影向量的夹角为π4.试求向量a .22223===34411cos cos cos 1cos ,cos ,42112112,,.222222a πππαγγαβγββ++===±⎧⎧⎪⎪±-±⎨⎨⎪⎪⎪⎪⎩⎭⎩⎭由已知得单位向量的分向量：，或由知从而所求向量为，，或11. 已知两点12(2,5,3),(3,2,5)M M --，点M 在线段12M M 上，且123M M MM =，求向径OM 的坐标.解：设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为，123M M MM =所以，11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 12. 已知点P 到点(0012)A ，，的距离是7，OP 的方向余弦是236,,777，求点P 的坐标.解：设P 的坐标为（x , y , z ）, 2222||(12)49PA x y z =++-=得2229524x y z z ++=-+122226570cos 6, 749z z z x y z γ==⇒==++ 又122222190cos 2, 749xx x x y z α==⇒==++ 122223285cos 3, 749y y y x y z β==⇒==++ 故点P 的坐标为P （2，3，6）或P （190285570,,494949）. 13. 已知,a b 的夹角2π3ϕ=，且3=a ， 4=b ，计算: (1) ⋅a b ；(2) (32)(2)-⋅+a b a b .解：（1）a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b14. 已知(4,2,4),(6,3,2)=-=-a b ，计算:(1) ⋅a b ； (2) (23)()-⋅+a b a b ；(3) 2-a b .解：（1）46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b36238499=-⨯+=15. 已知32,2=+-=-+a i j k b i j k ， 求: (1) ⨯a b ； (2) 27⨯a b ；(3) 72⨯b a ； (4) ⨯a a .解：（1） 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .16 已知向量a 和b 互相垂直，且3,4==a b ， 计算： (1) ()()+⨯-a b a b ；(2) (3)(2)+⨯-a b a b .解：（1）|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a bπ2||||sin242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin842=⨯⨯⨯= 习题7-31. 求过点(41,2)，-，且与平面32611x y z -+=平行的平面方程.解：所求平面与平面3x -2y +6z =11平行 故n ={3,-2,6}，又过点(4,1,-2)故所求平面方程为：3(x -4)-2(y -1)+6(z +2)=0 即3x -2y +6z +2=0.2. 求过点0(1,7,3)M -，且与连接坐标原点到点0M 的线段0OM 垂直的平面方程. 解：所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为：x -1+7(y -7)-3(z +3)=0 即x +7y -3z -59=03. 设平面过点(1,2,-1)，而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍，求此平面方程.解：设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上，则有121122b b b-++= 得b =2.故所求平面方程为1424x y z ++= 4. 求过(1,1,-1),(2,-2,2)-和(1,-1,2)三点的平面方程. 解：由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点，有1112121210111121x y z --+----+=---+化简得x -3y -2z =0即为所求平面方程.5. 指出下列各平面的特殊位置，并画出其图形： (1) 0y =； (2) 310x -=； (3) 2360x y --=； (4) 0x y -=； (5) 2340x y z -+=.解：(1) y =0表示xOz 坐标面（如图2） (2) 3x -1=0表示垂直于x 轴的平面.(如图3)图2 图3(3) 2x -3y -6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x =3和y =-2的平面.(如图4) (4) x –y =0表示过z 轴的平面（如图5）(5) 2x -3y +4z =0表示过原点的平面（如图6）.图4 图5 图66. 通过两点(1,1,1)和(2,2,2)作垂直于平面0x y z +-=的平面. 解：设平面方程为Ax +By +Cz +D =0 则其法向量为n ={A ,B ,C }已知平面法向量为n 1={1,1,-1} 过已知两点的向量l ={1,1,1} 由题知n ·n 1=0, n ·l =0 即00, .0A B C C A B A B C +-=⎧⇒==-⎨++=⎩所求平面方程变为Ax -Ay +D =0又点（1，1，1）在平面上，所以有D =0 故平面方程为x -y =0.7. 求通过下列两已知点的直线方程： (1)()1,2,1,(3,1,1)--；(2) (3,1,0),(1,0,3)--.解：（1）两点所确立的一个向量为s ={3-1，1+2，-1-1}={2，3，-2}故直线的标准方程为：121232x y z -+-==- 或 311232x y z --+==- （2）直线方向向量可取为s ={1-3，0+1，-3-0}={-2，1，-3}故直线的标准方程为：31213x y z -+==-- 或 13213x y z -+==-- 8. 求直线234035210x x z x y z +--=⎧⎨-++=⎩的标准式方程和参数式方程.解：所给直线的方向向量为 12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点（0，7，17），因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为：771719x t y t z t =⎧⎪=-⎨⎪=-⎩9. 决定参数k 的值，使平面29x ky z +-=适合下列条件： (1) 经过点(5,4,6)－；(2) 与平面230x y z -+=成π4的角. 解：（1） 因平面过点（5，-4，6） 故有 5-4k -2×6=9 得k =-4.（2） 两平面的法向量分别为 n 1={1,k ,-2} n 2={2,-3,1} 且122123π2cos cos ||||42514k k θ⋅-====+⋅n n n n 解得70k =±10. 确定下列方程中的l 和m ：(1) 平面2350x ly z ＋＋－＝和平面620mx y z --+=平行； (2) 平面3530x y lz -+-=和平面3250x y z +++=垂直. 解：（1）n 1={2,l ,3}, n 2={m ,-6,-1}12232,18613l m l m ⇒==⇒=-=--n n (2) n 1={3, -5, l }, n 2={1,3,2}12315320 6.l l ⊥⇒⨯-⨯+⨯=⇒=n n11. 通过点(11,1)，－作垂直于两平面10x y z -+-=和210x y z +++=的平面. 解：设所求平面方程为Ax +By +Cz +D =0其法向量n ={A ,B ,C }n 1={1,-1,1}, n 2={2,1,1}12203203A C A B C A B C CB ⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n n n n又（1，－1，1）在所求平面上，故A －B +C +D =0，得D =0故所求平面方程为2033CCx y Cz -++= 即2x -y -3z =012. 求平行于平面375x y z -+=，且垂直于向量2i j k －＋的单位向量. 解：n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n故1217733152122111--=⨯=++=+---n n n i j k i j k则1(52).30n =±+-e i j k 13. 求下列直线的夹角： (1) 533903210x y z x y z -+-=⎧⎨-+-=⎩和2223038180x y z x y z +-+=⎧⎨++-=⎩；(2) 2314123x y z ---==-和38121y z x --⎧=⎪--⎨⎪=⎩.解：（1）两直线的方向向量分别为：s 1={5, -3,3}×{3, -2,1}=533321ij k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直，夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是 12126cos 0.2064135785θθ⋅==≈⋅'≈︒s s s s 14. 求下列直线与平面的交点： (1) 11,2310126x y zx y z -+==++-=-；(2)213,2260232x y z x y z +--==+-+= 解：（1）直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为（2，-3，6）.（2） 直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为（-2，1，3）. 15. 求点(121)，，到平面22100x y z ++-=的距离.解：过点（1，2，1）作垂直于已知平面的直线，直线的方向向量为s =n ={1，2，2}所以垂线的参数方程为12212x ty t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =.故垂足为485(,,)333，且与点（1，2，1）的距离为222122()()()1333d =++= 即为点到平面的距离.习题7-41. 建立以点(13-2)，，为中心，且通过坐标原点的球面方程. 解：球的半径为22213(2)14.R =++-=设(x ,y ,z )为球面上任一点，则(x -1)2+(y -3)2+(z +2)2=14即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程. 2. 一动点离点(20-3)，，的距离与离点(4-6,6)，的距离之比为3，求此动点的轨迹方程. 解：设该动点为M (x ,y ,z )，由题意知222222(2)(0)(3) 3.(4)(6)(6)x y z x y z -+-++=-+++-化简得：8x 2+8y 2+8z 2-68x +108y -114z +779=0 即为动点的轨迹方程.3. 指出下列方程所表示的是什么曲面，并画出其图形：(1)2222a a x y ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭； （a 为正常数）(2)22149x y -+=；(3)22194x z +=；(4)20y z －＝； (5)220x y －＝；(6)220x y ＋＝.解：（1）母线平行于z 轴的抛物柱面，如图7. （2）母线平行于z 轴的双曲柱面,如图8.图7 图8 （3）母线平行于y 轴的椭圆柱面，如图9. （4）母线平行于x 轴的抛物柱面，如图10.图9 图10 （5）母线平行于z轴的两平面，如图11.（6）z轴，如图12.图11 图124. 指出下列方程表示怎样的曲面，并作出图形：(1)222149y zx++=；(2)22369436x y z+-=；(3)222149y zx--=；(4)2221149y zx+-=；(5)22209zx y+-=.解：（1）半轴分别为1，2，3的椭球面，如图13.(2) 顶点在（0，0，-9）的椭圆抛物面，如图14.图13 图14(3) 以x轴为中心轴的双叶双曲面，如图15.(4) 单叶双曲面，如图16.图15 图16(5) 顶点在坐标原点的圆锥面，其中心轴是z 轴，如图17.图175. 作出下列曲面所围成的立体的图形： (1)2222x y z a ＋＋＝与()0,02az z a ==>为常数； (2)4x y z =＋＋，0,1,0,2x x y y ====及0z =； (3)24,0,0,0z x x y z =-===及24x y +=； (4)226,0,0,0z x y x y z =-+===（）及1x y +=. 解：（1）（2）（3）（4）分别如图18，19，20， 1所示.图18 图19图20 图216. 求下列曲面和直线的交点：(1)222181369x y z ++=与342364x y z --+==-； (2)22211694x y z +-=与2434x y z +==-. 解：（1）直线的参数方程为334624x t y t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1. 得交点坐标为（3，4，-2），（6，-2，2）. (2) 直线的参数方程为4324x t y tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1, 得交点坐标为（4，-3，2）.7. 设有一圆，它的中心在z 轴上、半径为3，且位于距离xOy 平面5个单位的平面上，试建立这个圆的方程.解：设（x ，y ，z ）为圆上任一点，依题意有2295x y z ⎧+=⎨=±⎩ 即为所求圆的方程.8. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状，并写出其方程.(1) 平面2x =； (2) 平面0y =； (3) 平面5y =； (4) 平面2z =.解：（1）截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.（2）截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ⎧==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.9. 求曲线2222222,x y z a x y z ＋＋＝＋＝在xOy 面上的投影曲线. 解：以曲线为准线，母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩10. 建立曲线22,1x y z z x ＋＝＝＋在xOy 平面上的投影方程. 以曲线为准线，母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=. 故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题七1.填空题：（1）过(0,1,0)且与平面1x y z -+=平行的平面方程为1x y z -+=-（2）点(2,1,0)到平面3450x y z ++=的距离（3）原点关于平面6291210x y z +-+=的对称点是 （-12，-4，18） 。

第五篇 向量代数与空间解析几何第八章 向量代数与空间解析几何解析几何的基本思想是用代数的方法来研究几何的问题，为了把代数运算引入几何中来，最根本的做法就是设法把空间的几何结构有系统的代数化，数量化. 平面解析几何使一元函数微积分有了直观的几何意义，所以为了更好的学习多元函数微积分，空间解析几何的知识就有着非常重要的地位.本章首先给出空间直角坐标系，然后介绍向量的基础知识，以向量为工具讨论空间的平面和直线，最后介绍空间曲面和空间曲线的部分容.第1节 空间直角坐标系1.1 空间直角坐标系用代数的方法来研究几何的问题，我们需要建立空间的点与有序数组之间的联系，为此我们通过引进空间直角坐标系来实现.1.1.1 空间直角坐标系过定点O ，作三条互相垂直的数轴，这三条数轴分别叫做x 轴(横轴）、y 轴(纵轴)、z 轴(竖轴)，它们都以O 为原点且具有相同的长度单位. 通常把x 轴和y 轴配置在水平面上，而z 轴则是铅垂线；它们的正方向要符合右手规则：右手握住z 轴，当右手的四指从x 轴的正向转过2角度指向y 轴正向时，大拇指的指向就是z 轴的正向，这样就建立了一个空间直角坐标系（图8-1），称为Oxyz 直角坐标系，点O 叫做坐标原点.图8-1在Oxyz 直角坐标系下，数轴Ox ,Oy ,Oz 统称为坐标轴，三条坐标轴中每两条可以确定一个平面，称为坐标面，分别为xOy ，yOz ，zOx ，三个坐标平面将空间分为八个部分，每一部分叫做一个卦限（图8-2），分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ表示.yxzO图8-21.1.2 空间点的直角坐标设M 为空间中的任一点，过点M 分别作垂直于三个坐标轴的三个平面，与x 轴、y 轴和z 轴依次交于A 、B 、C 三点，若这三点在x 轴、y 轴、z 轴上的坐标分别为x ，y ，z ，于是点M 就唯一确定了一个有序数组(, , )x y z ，则称该数组(, , )x y z 为点M 在空间直角坐标系Oxyz 中的坐标，如图8-3．x ，y ，z 分别称为点M 的横坐标、纵坐标和竖坐标．图8-3反之，若任意给定一个有序数组(, , )x y z ，在x 轴、y 轴、z 轴上分别取坐标为x ，y ，z 的三个点A 、B 、C ，过这三个点分别作垂直于三个坐标轴的平面，这三个平面只有一个交点M ，该点就是以有序数组(, , )x y z 为坐标的点，因此空间中的点M 就与有序数组(, , )x y z 之间建立了一一对应的关系．注：A 、B 、C 这三点正好是过M 点作三个坐标轴的垂线的垂足．yxzOyxzAB C(,,)M x y z1.2 空间中两点之间的距离设两点111(, , )M x y z ，222(, , )N x y z ，则M 与N 之间的距离为212212212)()()(z z y y x x d -+-+-= （8-1-1）事实上，过点M 和N 作垂直于xOy 平面的直线，分别交xOy 平面于点1M 和1N ，则1MM ∥1NN ，显然，点1M 的坐标为11(, , 0)x y ，点1N 的坐标为22(, , 0)x y （如图8-4）．图8-4由平面解析几何的两点间距离公式知，1M 和1N 的距离为：21221211)()(||y y x x N M -+-=．过点M 作平行于xOy 平面的平面，交直线1NN 于2N ，则11M N ∥2MN ，因此2N 的坐标为221(, , )x y z ，且212212112)()(||||y y x x N M MN -+-==，在直角三角形N MN 2中，||||122z z N N -=，所以点M 与N 间的距离为2122122122222)()()(||||z z y y x x N N MN d -+-+-=+=．例1 设(1, 2, 0)A -与(1, 0, 2)B --为空间两点，求A 与B 两点间的距离． 解 由公式（8-1-1）可得，A 与B 两点间的距离为d ==例2 在z 轴上求与点(3, 5, 2)A -和(4, 1, 5)B -等距的点M ．解 由于所求的点M 在z 轴上，因而M 点的坐标可设为(0, 0, )z ，又由于MA MB =，由公式（8-1-1），得222222)5(1)4()2(53z z -++-=--++．从而解得72=z ，即所求的点为2(0, 0, )7M ．习题8-11．讨论空间直角坐标系的八个卦限中的点的坐标的符号． 2．在坐标轴上的点和在坐标平面上的点的坐标各有何特点？ 3．在空间直角坐标系中，画出以下各点：(2, 0, 0)A ；(0, 3, 0)B -；(3, 0, 1)C ；(3, 2, 1)D -．4．求点(1, 2, 3)-关于各坐标平面对称的点的坐标． 5．求点(1, 2, 3)关于各坐标轴对称的点的坐标． 6．求以下各对点间的距离： (1) (0, 1, 3)A -与(2, 1, 4)B ；(2) (1, 4, 2)C -与D(2, 7, 3)．7．在坐标平面yOz 上求与三点(3, 1, 2)A 、(4, 2, 2)B --和(0, 5, 1)C 等距的点． 8．求点(12, 3, 4)A -与原点、各坐标平面和各坐标轴的距离．9. 证明以()()()A 4,3,1,B 7,1,2,C 5,2,3为顶点的三角形△ABC 是一等腰三角形.第2节 空间向量的代数运算2.1 空间向量的概念在日常生活中，我们经常会遇到一些量，如质量、时间、面积、温度等，它们在取定一个度量单位后，就可以用一个数来表示．这种只有大小没有方向的量，叫做数量（或标量）．但有一些量，如力、位移、速度、电场强度等，仅仅用一个实数是无法将它们确切表示出来，因为它们不仅有大小，而且还有方向，这种既有大小又有方向的量，叫做向量（或矢量）．在数学上，我们用有向线段AB 来表示向量，A 称为向量的起点，B 称为向量的终点，有向线段的长度就表示向量的大小，有向线段的方向就表示向量的方向．通常在印刷时用黑体小写字母a ，b ，c ，…来表示向量，手写时用带箭头的小写字母, ,,a b c来记向量.向量的长度称为向量的模，记作a 或AB ，模为1的向量叫做单位向量，模为0的向量叫做零向量，记作0，规定：零向量的方向可以是任意的．本章我们讨论的是自由向量，即只考虑向量的大小和方向，而不考虑向量的起点，因此，我们把大小相等，方向相同的向量叫做相等向量，记作a =b .规定：所有的零向量都相等.与向量a 大小相等，方向相反的向量叫做a 的负向量(或反向量)，记作 a ． 平行于同一直线的一组向量称为平行向量（或共线向量）．平行于同一平面的一组向量，叫做共面向量，零向量与任何共面的向量组共面.2.2 向量的线性运算2.2.1 向量的加法我们在物理学中知道力与位移都是向量，求两个力的合力用的是平行四边形法则，我们可以类似地定义两个向量的加法．定义1 对向量a ，b ，从同一起点A 作有向线段AB 、AD 分别表示a 与b ，然后以AB 、AD 为邻边作平行四边形ABCD ，则我们把从起点A 到顶点C 的向量AC 称为向量a 与b 的和（图8-5），记作a +b ．这种求和方法称为平行四边形法则．图8-5 图8-6若将向量b 平移，使其起点与向量a 的终点重合，则以a 的起点为起点，b 的终点为终ab Cabc =a +b点的向量c 就是a 与b 的和(图8-6），该法则称为三角形法则．多个向量，如a 、b 、c 、d 首尾相接，则从第一个向量的起点到最后一个向量的终点的向量就是它们的和a +b +c +d （图8-7）．图8-7对于任意向量a ，b ，c ，满足以下运算法则： (1)a +b =b +a (交换律)．(2)()()a +b +c =a +b +c (结合律)． (3)0a +=a ．2.2.2 向量的减法定义2 向量a 与b 的负向量-b 的和，称为向量a 与b 的差，即()--a b =a +b ．特别地，当b =a 时，有()-0a +a =.由向量减法的定义，我们从同一起点O 作有向线段OA ，OB 分别表示a ，b ，则()OA OB OA OB --=+-a b =OA BO BA =+=．也就是说，若向量a 与b 的起点放在一起，则a ，b 的差向量就是以b 的终点为起点，以a 的终点为终点的向量（图8-8）．图8-82.2.3数乘向量定义3 实数λ与向量a 的乘积是一个向量，记作λa ，λa 的模是λa ，方向： 当0λ>时，λa 与a 同向；当0λ<时，λa 与a 反向；当0λ=时，λ0a =．abcda +b +c +daabb -a bBAC对于任意向量a ，b 以与任意实数λ，μ，有运算法则： (1) ()()λμλμa =a ． (2) ()+λμλμ+a =a a ．(3) ()+λλλ+a b =a b ．向量的加法、减法与数乘向量运算统称为向量的线性运算，λμa +b 称为a ，b 的一个线性组合(, )R λμ∈．特别地，与 a 同方向的单位向量叫做a 的单位向量，记做a e ，即aa e a=.上式说明：一个非零向量除以它的模的结果是一个与原向量同方向的单位向量.例1 如图8-9，在平行六面体///ABCD B C D /—A 中，设/=AA ,a AD =b AB =c ,试用,,a b c 来表示对角线向量//,.AC A C图8-9解 ''AC AB BC CC =++'AB BC AA =++a b c =++；'''AC A A AB BC AA AB AD =++=-++a b c =++.由于向量λa 与a 平行，所以我们通常用数与向量的乘积来说明两个向量的平行关系.即有,定理1 向量a 与非零向量b 平行的充分必要条件是存在一个实数λ，使得λa =b .2.3 向量的坐标表示2.3.1向量在坐标轴上的投影设A 为空间中一点，过点A 作轴u 的垂线，垂足为'A ，则'A 称为点A 在轴u 上的投影(图8-10)．图8-10若M 为空间直角坐标系中的一点，则M 在x 轴、y 轴、z 轴上的投影为A 、B 、C ，如图8-11所示．图8-11设向量AB 的始点与终点B 在轴u 的投影分别为A '、B '，那么轴u 上的有向线段A B ''的值A B ''叫做向量AB 在轴u 上的投影，记作u prj AB A B ''=，轴u 称为投影轴.图8-12当A B ''与轴u 同向时，投影取正号，当A B ''与轴u 反向时，投影取负号． 注 (1) 向量在轴上投影是标量．(2) 设MN 为空间直角坐标系中的一个向量，点M 的坐标为111(, , )x y z ，点N 的坐标为222(, , )x y z ，显然，向量MN 在三个坐标轴上的投影分别为12x x -，12y y -，12z z -． 2.3.2向量的坐标表示yxzOA B CM取空间直角坐标系Oxyz ，在x 轴、y 轴、z 轴上各取一个与坐标轴同向的单位向量，依次记作, , i j k ，它们称为坐标向量．空间中任一向量a ，它都可以唯一地表示为, , i j k 数乘之和． 事实上，设MN a =，过M 、N 作坐标轴的投影，如图8-13所示．MN =MA+AP +PN =MA+MB +MC a =．由于MA 与i 平行，MB 与j 平行，MC 与k 平行，所以，存在唯一的实数, , x y z ，使得MA x =i ，MB y =j ，MC z =k ，即x y z a =i +j +k ． (8-2-1)图 8-13我们把(8-2-1)式中, , i j k 系数组成的有序数组(, , )x y z 叫做向量a 的直角坐标，记为{, , }x y z a =，向量的坐标确定了，向量也就确定了．显然，(8-2-1)中的, , x y z 是向量a 分别在x 轴、y 轴、z 轴上的投影．因此，在空间直角坐标系中的向量a 的坐标就是该向量在三个坐标轴上的投影组成的有序数组．例2 在空间直角坐标系中设点(3, 1, 5)M -，(2, 3, 1)N -，求向量MN 与NM 的直角坐标．解 由于向量的坐标即为向量在坐标轴上的投影组成的有序数组，而向量的各投影即为终点坐标与起点坐标对应分量的差．所以向量MN 的坐标为{5, 4, 4}--，向量NM 的坐标为{5, 4, 4}-． 例3(定比分点公式) 设111(,,)A x y z 和222(,,)B x y z 为两已知点，有向线段AB 上的点M 将它分为两条有向线段AM 和MB ，使它们的值的比等于数(1)λλ≠-，即AMMBλ=，求分点(,,)M x y z 的坐标.图8-14 解 如图8-14，因为AM 与MB 在同一直线上，且同方向，故AM MB λ=⋅，而122{,,}AM x x y y z z =---， 222{,,}MB x x y y z z =---222{(),(),()}MB x x y y z z λλλλ=---所以 12()x x x x λ-=-，12()y y y y λ-=-，12()z z z z λ-=- 解得121212,,.111x x y y z z x y z λλλλλλ+⋅+⋅+⋅===+++当λ=1, 点M 的有向线段→AB x 2.3.3向量可以用它的模与方向来表示，设空间向量12a M M =分别为,,αβγ，规定： 0,0απ≤≤≤称,,αβγ为向量a 的方向角因为向量a 12cos cos x a M M a αα=⋅=⋅12cos cos y a M M a ββ=⋅=⋅(8-2-2)12cos cos z a M M a γγ=⋅=⋅公式(8.2.2)中出现的cos ,cos ,cos αβγ称为向量a 的方向余弦.而{,,}{cos ,cos ,cos }x y z a a a a a a a αβγ==⋅⋅⋅{cos ,cos ,cos }a a a e αβγ=⋅=⋅{cos ,cos ,cos }a e αβγ=是与向量a 同方向的单位向量.而 a =M M =12,,x y z M P a M Q a M R a ===111，故向量a 的模为 x a a a =+2(8-2-3)从而向量a 的方向余弦为cos a αβγ===(8-2-4)并且 222cos cos cos 1αβγ++=.例4 已知两点1M 和()21,3,0M ,求向量12M M 的模、方向余弦和方向角.解12(12,32,0(1,1,M M =--=-2)2(1)1(222=-++-=；11cos ,cos ,cos 22αβγ=-==； 23,,334πππαβγ===. 例5 已知两点(4,0,5)A 和(7,1,3)B ，求与AB 同方向的单位向量e . 解 因为{74,10,35}{3,1,2},AB =---=-所以23AB == 于是 {}.e =2.4 向量的数量积在物理中我们知道，一质点在恒力F 的作用下，由A 点沿直线移到B 点，若力F 与位移向量AB 的夹角为θ，则力F 所作的功为||||cos W F AB θ=⋅⋅．类似的情况在其他问题中也经常遇到．由此，我们引入两向量的数量积的概念． 定义1 设a ，b 为空间中的两个向量，则数cos ,a b a b叫做向量a 与b 的数量积(也称积或点积)，记作⋅a b ，读作“a 点乘b ”．即cos ,⋅a b =a b a b （8-2-5）其中,a b 表示向量a 与b 的夹角，并且规定0, π≤≤a b ．两向量的数量积是一个数量而不是向量，特别地当两向量中一个为零向量时，就有0⋅a b =.由向量数量积的定义易知：(1)2⋅a a =a ，因此=a(2) 对于两个非零向量a ，b ，a 与b 垂直的充要条件是它们的数量积为零，即⊥a b ⇔0⋅a b =．注 数量积在解决有关长度、角度、垂直等度量问题上起着重要作用． 数量积的运算满足如下运算性质： 对于任意向量a ，b 与任意实数λ，有 (1) 交换律：⋅⋅a b =b a ．(2) 分配律：()⋅⋅⋅a b +c =a b +a c ．(3) 与数乘结合律：()()()λλλ⋅⋅=⋅a b =a b a b ． (4)0⋅≥a a 当且仅当0a =时，等号成立．例6 对坐标向量i ，j ，k ，求⋅i i ，⋅j j ，⋅k k ，⋅i j ，⋅j k ，⋅k i ． 解 由坐标向量的特点与向量积的定义得1⋅⋅⋅i i =j j =k k =， 0⋅⋅⋅i j =j k =k i =．例7 已知2=a ，3=b ，2, 3π=a b ，求a b ⋅，(2)()-+a b a b ⋅，+a b ． 解 由两向量的数量积定义有2cos , 23cos 3π⋅=⨯⨯a b =a b a b 123()=32=⨯⨯--．(2)()=22-⋅+⋅⋅-⋅-⋅a b a b a a +a b b a b b22=2-⋅-a a b b 222(3)23=11=---⨯-．2()()+=⋅+a b a +b a b =⋅⋅+⋅+⋅a a +a b b a b b222=+⋅+a a b b 2222(3)3=7=+⨯-+，因此+=a b ．在空间直角坐标系下，设向量111{,,}x y z a =，向量222{,,}x y z b =，即111x y z ++a =i j k , 222x y z ++b =i j k ．则111222()()x y z x y z ⋅++⋅++a b =i j k i j k121212()()+()x x x y x z ⋅+⋅⋅=i i i j i k 121212()()+()y x y y y z ⋅+⋅⋅+j i j j j k 121212()()+()z x z y z z ⋅+⋅⋅+k i k j k k ．由于1⋅⋅⋅i i =j j =k k =， 0⋅⋅⋅i j =j k =k i =，所以121212x x y y z z ⋅++a b =．(8-2-6)也就是说，在直角坐标系下，两向量的数量积等于它们对应坐标分量的乘积之和．同样，利用向量的直角坐标也可以求出向量的模、两向量的夹角公式以与两向量垂直的充要条件，即设非零向量111{,,}x y z a =，向量222{,,}x y z b =，则=a (8-2-7)cos ||||⋅=a ba,b a b=． (8-2-8)⊥a b ⇔1212120x x y y z z ++=． (8-2-9)例8 在空间直角坐标系中，设三点(5, 4, 1)A -，(3, 2, 1)B ，(2, 5, 0)C -．证明:ABC ∆是直角三角形．证明 由题意可知{2, 6, 0}AB =-，={3, 1, 1}AC ---，则(2)(3)6(1)0(1)0AB AC ⋅=-⨯-+⨯-+⨯-=，所以AB AC ⊥．即ABC ∆是直角三角形．2.5向量的向量积在物理学中我们知道，要表示一外力对物体的转动所产生的影响，我们用力矩的概念来描述．设一杠杆的一端O 固定，力F 作用于杠杆上的点A 处，F 与OA 的夹角为θ，则杠杆在F 的作用下绕O 点转动，这时，可用力矩M 来描述．力F 对O 的力矩M 是个向量，M 的大小为||||||sin OA OA =M F ,F ．M 的方向与OA 与F 都垂直，且OA ，F ，M 成右手系，如图8-16所示．图8-162.5.1向量积的定义在实际生活中，我们会经常遇到象这样由两个向量所决定的另一个向量，由此，我们引入两向量的向量积的概念．定义2 设a ，b 为空间中的两个向量，若由a ，b 所决定的向量c ，其模为sin , c =a b a b ． (8-2-10)其方向与a ，b 均垂直且a ，b ，c 成右手系（如图8-17），则向量c 叫做向量a 与b 的向量积(也称外积或叉积)．记作⨯a b ，读作“a 叉乘b ”．注 (1) 两向量a 与b 的向量积⨯a b 是一个向量，其模⨯a b 的几何意义是以a ，b 为邻边的平行四边形的面积． (2)⨯0a a =这是因为夹角θ=0，所以⨯0a a = 图8-17(3)对两个非零向量a 与b ，a 与b 平行(即平行)的充要条件是它们的向量积为零向量．a ∥b ⇔⨯0a b =．向量积的运算满足如下性质：对任意向量a ，b 与任意实数λ，有 (1) 反交换律：⨯-⨯a b =b a ． (2) 分配律:()⨯⨯⨯a b +c =a b +a c ，()⨯⨯⨯a +b c =a c +b c ．(3) 与数乘的结合律：()()()λλλ⨯⨯⨯a b =a b =a b ．例9 对坐标向量i ，j ，k ，求⨯i i ，⨯j j ，⨯k k ，⨯i j ，⨯j k ，⨯k i ． 解⨯⨯⨯0i i =j j =k k =．⨯i j =k ，⨯j k =i ，⨯k i =j ．2.5.2向量积的直角坐标运算在空间直角坐标系下，设向量111{, , }x y z a =，向量222{, , }x y z b =，即111x y z ++a =i j k ，222x y z ++b =i j k ，因为⨯⨯⨯0i i =j j =k k =． ⨯i j =k ，⨯j k =i ，⨯k i =j ， ⨯-j i =k ，⨯-k j =i ，⨯-i k =j ．则111222()()x y z x y z ⨯++⨯++a b =i j k i j k121212()()+()x x x y x z ⨯+⨯⨯=i i i j i k 121212()()+()y x y y y z ⨯+⨯⨯+j i j j j k 121212()()+()z x z y z z ⨯+⨯⨯+k i k j k k121212121212()()+()()()()x y y x y z z y x z z x -⨯-⨯--⨯=i j j k k i 121212121212()()+()y z z y x z z x x y y x ----=i j k ．为了便于记忆，借助于线性代数中的二阶行列式与三阶行列式有111111222222y z x z x y y z x z x y ⨯-a b =i j +k 111222x y z x y z =i j k ． 注 设两个非零向量111{, , }x y z a =，222{, , }x y z b =，则a ∥b ⇔⨯0a b =，⇔212121z z y y x x ==． 若某个分母为零，则规定相应的分子为零．例10 设向量{1,2,1}--a =，{2,0,1}b =，求⨯a b 的坐标．解211112121012120201----⨯--=-i j ka b =i j +k 234=--i j +k ．因此⨯a b 的直角坐标为{2, 3, 4}--．例11 在空间直角坐标系中，设向量{3, 0, 2}a =，{1, 1, 1}--b =，求同时垂直于向量a 与b 的单位向量．解 设向量⨯c =a b ，则c 同时与a ，b 垂直．而302111⨯--i j kc =a b =23=-+i j +k ，所以向量c 的坐标为{2, 1, 3}-．再将c 单位化，得02,1,3}={=-c ，即{与-- 为所求的向量． 例12 在空间直角坐标系中，设点(4, 1, 2)A -，(1, 2, 2)B -，(2, 0, 1)C ，求ABC ∆的面积．解 由两向量积的模的几何意义知：以AB 、AC 为邻边的平行四边形的面积为AB AC ⨯，由于{3, 3, 4}AB =--，{2, 1, 1}AC =--，因此33453211AB AC ⨯=--=++--i j ki j k ，所以21AB AC ⨯=故ABC ∆的面积为235=∆ABC S ．2.6向量的混合积定义3 给定空间三个向量,,a b c ，如果先作前两个向量a 与b 的向量积，再作所得的向量与第三个向量c 的数量积，最后得到的这个数叫做三向量,,a b c 的混合积，记做()a b c ⨯⋅或abc ⎡⎤⎣⎦.说明：三个不共面向量,,a b c 的混合积的绝对值等于以,,a b c 为棱的平行六面体的体积V .定理如果111a X i Y j Z k =++，222b X i Y j Z k =++，333c X i Y j Z k =++，那么 111222333.X Y Z abc X Y Z X Y Z ⎡⎤=⎣⎦习题8-21.,,,,,().ABCD AB AD AC DB MA M ==设为一平行四边形试用表示为平行四边形对角线的交点a b.a b12.,().2M AB O OM OA OB =+设为线段的中点,为空间中的任意一点证明 2223.?(1)()();(2)();(3)()().==⨯=⨯对于任意三个向量与判断下列各式是否成立a,b c,a b c b c a a b a b a b c c a b4.:(1);(2)(3).利用向量证明三角形的余弦定理正弦定理；勾股定理5.设,,a b c 为单位向量,且满足0a b c ++=,求.a b b c c a ++6.1(3,2,2),(1,3,2),(8,6,2),322a b c a b + c.求=-==--7.已知三点(3,0,2),A B AB ==求的坐标、模、方向余弦和方向角.8.一向量的终点在点B(2,-1,7),它在x 轴、y 轴和z 轴上的投影依次为4，-4和7.求这向量的起点A 的坐标.9．设2=a ，4=b ，3πa,b =，求⋅a b ，(2)-⋅a b b ，-a b ． 10．设向量a ，b ，c 两两垂直，且1=a ，2=b ，3=c ，求向量d =a +b +c 的模与d,a ．11．在空间直角坐标系中，已知{1,2,3}-a = ，{2,2,1}-b = ，求： (1)⋅a b ；(2) 25⋅a b ；(3) a ；(4)cos a,b ．12.已知向量2332和,,a i j k b i j k c i j =-+=-+=-，计算 （1）()();a b c a c b -（2）()();a b b c +⨯+（3）()a b c ⨯.13．设向量a ，b 的直角坐标分别为{1, 3, 2}--和{2, 4, }k -，若a b ⊥，求k 的值．14．设向量{2, 1, 1}-a =，{1, 3, 0}-b =，求以、a b 为邻边构造的平行四边形面积． 15．求同时垂直于向量{3, 2, 4}-a =和纵轴的单位向量．16．已知三角形三个顶点(4, 1, 2)A -，(3, 0, 1)B -，(5, 1, 2)C ，求ABC ∆的面积．第3节 空间中的平面与直线方程在本节我们以向量为工具，在空间直角坐标系中讨论最简单的曲面和曲线——平面和直线.3.1平面与其方程首先利用向量的概念，在空间直角坐标系中建立平面的方程，下面我们将给出几种由不同条件所确定的平面的方程．3.1.1平面的点法式方程若一个非零向量n 垂直于平面π，则称向量n 为平面π的一个法向量．显然，若n 是平面π的一个法向量，则λn (λ为任意非零实数)都是π的法向量，即平面上的任一向量均与该平面的法向量垂直．由立体几何知识知道，过一个定点0000(, , )M x y z 且垂直于一个非零向量{, , }A B C n =有且只有一个平面π．设(, , )M x y z 为平面π上的任一点，由于π⊥n ，因此0M M ⊥n ．由两向量垂直的充要条件，得00M M =⋅n ,而0000{, , }M M x x y y z z =---，{, , }A B C n =，所以可得0)()()(000=-+-+-z z C y y B x x A ． (8-3-1)由于平面π上任意一点(, , )M x y z 都满足方程(8-3-1)，而不在平面π上的点都不满足方程(8-3-1)，因此方程(8-3-1)就是平面π的方程．由于方程(8-3-1)是给定点0000(, , )M x y z 和法向量{, , }A B C n =所确定的，因而称式(8-3-1)叫做平面π的点法式方程．图8-18例1 求通过点0(1, 2, 4)M -且垂直于向量{3, 2, 1}-n =的平面方程．解 由于{3, 2, 1}-n =为所求平面的一个法向量，平面又过点0(1, 2, 4)M -，所以，由平面的点法式方程(6-14)可得所求平面的方程为3(1)2(2)1(4)=0x y z --⋅++⋅-，整理，得32110x y z -+-=．例2 求过三点()12,1,4M -，()2M 1,3,2--，()3M 0,2,3 的平面π的方程． 解 所求平面π的法向量必定同时垂直于12M M 与13M M ．因此可取12M M 与13M M 的向量积1213M M M M ⨯为该平面的一个法向量n ．即1213n =M M M M ⨯．由于12{3, 4, 6}M M =--，13{2, 3, 1}M M =--，因此1213-631i j kn =M M M M =342⨯---149i j k,=+-,因此所求平面π的方程为0419214=--++-)()()(z y x ，化简得.015914=--+z y x一般地，过三点(,,)(1,2,3)k k k k M x y z k =的平面方程为1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 称为平面的三点式方程。

第一章空间解析几何与向量代数考点一：空间直角坐标系1．空间直角坐标系建立过空间定点O作三条垂直的数轴，以O为原点，具有相同单位长度，三条数轴分别为x轴、y轴、z轴，统称坐标轴。

三条坐标轴的任意两条都可确定一个平面，称为坐标面。

分别是x和y确定的Oxy平面，y和z确定的Oyz平面,x和z确定的Oxz平面。

三个相互垂直的坐标面把空间分为八个部分，每一部分称为一个卦象。

2．空间中两点间的距离公式设空间两点（）,（）,他们两点之间的距离为：||==。

特别地，点P（x，y，z）到原点O（0，0，0）的距离|OP|=。

考点二：向量代数1.向量的概念由数值决定大小的量，如：质量，温度，面积，密度等，称之为标量（数量）。

有大小还有方向，如：力，加速度，速度等，称之为向量。

空间中以A为起点，B为终点的线段称为有向线段，记为，简记为，将向量的长度记为||或||，称为向量的模。

如果向量的模为零，称为零向量。

定义1：如果两个向量与的长度相等且方向相同，则称这两个向量是相等的向量，记作=。

一个向量在空间中平移到任何位置而得到的向量与原向量相等，称为自由向量。

将若干个向量起点平移到同一个点后，它们的起点和终点都位于同一直线上，则称向量是共线的；起点和终点都位于同一个平面上，则称这些向量是共面的。

不论长度大小，两向量与的方向相反或相同，称与平行，记为。

2.向量的加法平行四边形法则：给定两个向量与，平移到同一个O点，设它们终点为A和B，则=，=，以，为邻边构造一个平行四边形OBCA。

以O为起点C为终点的向量=称为向量与的和，记为+=，即+=。

三角形法则：给定两个向量与，将平移，使其起点平移到的终点，此时的终点与用平行四边形法则确定的点C重合，从而=，于是与的和为+=。

零向量起点与终点重合，对于任何向量，三角形法则可得+0=。

向量加法的逆运算称为向量减法。

给定向量与，如存在使得=，则称是向量与的差，记为-=。

设=，=，有三角形法则可知=+，于是-=。

《高等数学》课程介绍一、课程简介高等数学是一门重要的数学基础课程，是理工科、经济金融等专业的重要必修课。

本课程旨在培养学生掌握高等数学的基本概念、方法和技能，提高学生的数学素养和解决实际问题的能力。

通过本课程的学习，学生将掌握微积分、线性代数、空间解析几何等基础知识，为后续课程的学习打下坚实的基础。

二、课程目标本课程的目标是让学生掌握高等数学的基本概念、方法和技能，提高学生的数学素养和解决实际问题的能力。

具体来说，学生需要掌握极限、导数、微分、积分等基本概念，学会运用这些概念解决函数单调性、最值、极值等问题；掌握矩阵、行列式等基本概念和运算方法，学会运用这些概念解决线性方程组、矩阵变换等问题；掌握空间解析几何的基本概念和方法，学会运用这些概念解决几何问题。

三、课程内容本课程主要包括微积分、线性代数和空间解析几何三个部分。

1.微积分部分包括函数、极限、连续、导数、微分、不定积分和定积分等内容。

通过学习这些内容，学生将掌握函数的基本性质和运算方法，学会运用极限和导数解决函数单调性、极值等问题，掌握不定积分和定积分的计算方法。

2. 线性代数部分包括矩阵、行列式、向量组等内容。

通过学习这些内容，学生将掌握矩阵的基本概念和运算方法，学会运用行列式解决线性方程组等问题，掌握向量组的基本概念和方法，学会运用向量组解决几何问题。

3. 空间解析几何部分包括向量代数、空间直角坐标系、平面与直线等内容。

通过学习这些内容，学生将掌握向量代数的基本概念和方法，学会运用空间直角坐标系解决几何问题，掌握平面与直线的基本性质和方法。

四、教学方法与手段本课程采用多种教学方法和手段，包括课堂讲授、案例分析、小组讨论、课堂互动等。

教师将根据教学内容和学生实际情况选择合适的教学方法，以提高学生的学习积极性和教学效果。

同时，教师还将利用多媒体教学技术，通过图片、视频等形式展示教学内容，帮助学生更好地理解和掌握知识。

五、考核方式本课程的考核方式包括平时成绩和期末考试成绩两部分。