§6.3 泰勒公式 数学分析课件(华师大四版) 高教社ppt 华东师大教材配套课件
- 格式:pps
- 大小:2.26 MB
- 文档页数:34









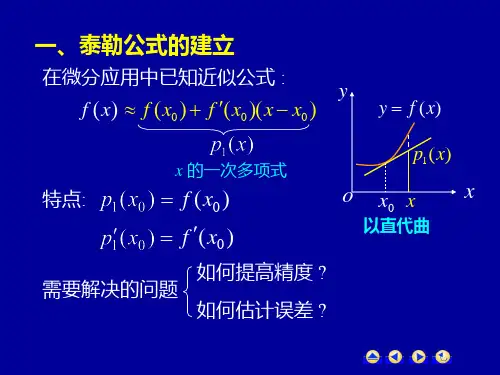

带有拉格朗日型余项的泰勒公式 在近似计算中的应用)(x f 设 在 0x x =处可导, 0000()()()()().f x f x f x x x o x x '=+-+-当 ||0x x -充分小时, )(x f 可以由一次多项式))(()(000x x x f x f -'+其误差为 0().o x x -带有佩亚诺型余项的泰勒公式)(0x x o -是不够的, 而要考虑用较高次 误差仅为 的多项式来逼近 f , 使得误差更小, 0(()).no x x -如由有限增量公式近似地代替, 但在许多情况下, 后退 前进 目录 退出§3 泰勒公式 带有佩亚诺型余项的泰勒公式问题: 是否存在一个 n 次多项式 ),(x P n 使得?))(()()(no n x x o x P x f -=-答案: 当 f (x )在点 x 0 有n 阶导数时, 这样的 n 次多 设0100()()(),nn n P x a a x x a x x =+-++-则有什么关系? 现在来分析这样的多项式与 f (x ) 项式是存在的. ,!)(0)(n n n a n x P =,)(00a x P n =,)(10a x P n =',!2)(20a x P n ='',即 ()0().!n n n P x a n =上式表明 P n (x ) 的各项系数是由其在点 x 0 的各阶设 f (x ) 在 x 0 处 n 阶可导. 导数所确定的.),(00x P a n =,!1)(01x P a n '=,!2)(02x P a n ''=,即00()()lim 0,()n n x x f x P x x x →-=-),)(()()(0nn x x o x P x f -=-如果则不难得到:,,,2,1,0),()(0)(0)(n k x P x fk n k ==)1(000()()()()1!n f x T x f x x x '=+-++0.k 其中表示不求导=)2(()00()().!n nfx x x n +- 为 f (x ) 在点 x 0 的 n 阶泰勒多项式, 为泰勒系数.()0()(0,1,,)!k fx k n k =这时称称)(x T n 确实是我们所需要的多项式.定理6.8设 f (x ) 在 x = x 0 处有n 阶导数,则,))(()()(0nn x x o x T x f -+=即+-''+-'+=200000)(!2)()(!1)()()(x x x f x x x f x f x f ).)(()(!)(000)(nn n x x o x x n x f -+-+ )3(故只需证0()()lim 0.()()n n n x x n R x R x Q x x x →=-证 设 ,)()(,)()()(0nn n n x x x Q x T x f x R -=-=因为 ,0)()()(0)(00==='=x R x R x R n n nn (1)()0000()()()0,()!n n n nnn Q x Q x Q x Q x n -'=====则当 ,时且00)(x x x U x →∈连续使用 n –1 次洛 必达法则, 得到()()()n n R x f x T x =-()()()()()()k k k nn R x fx T x =-所以100)()(lim )()(lim 0-→→-'=-n nxx n n x x x x n x R x x x R )(!)(lim 0)1(0x x n x R n n x x -==-→0(1)(1)()0000()()()()1lim !n n n x x f x fx fx x x n x x --→⎡⎤---=⎢⎥-⎣⎦)(x f )3(式称为 在点 0x 处的带有佩亚诺型余项的 n阶泰勒公式.注1 0)(x x f 在点即使附近满足)4())(()()(0nn x x o x P x f -+=0.=也不能说明 )(x P n 一定是 f (x ) 的n 阶泰勒多项式.0(1)(1)()000()()1lim ()!n n n x x f x f x f x n x x --→⎡⎤-=-⎢⎥-⎣⎦,0)(,)()(1=⋅=+x P xx D x f n n 00=x 在处满足 (4). )(x P n 不是f (x ) 在点 的 n 阶泰勒多项式, 00=x 在点 x = 0 的高阶导数(二阶和二阶以上)都不存 比如所以无法构造 n 阶多项式.但是当 n > 1 时, 原因是 f (x )在, ).)(()()(0nn x x o x T x f -+=注2 若 f (x ) 在点 x 0 有n 阶导数, 项式 ( 泰勒多项式 T n (x ) ) 满足:则只有惟一的多注3 可以证明对任意一个n 次多项式 ,)(x P n ),(0x U 使得).(,|)()(||)()(|0x U x x P x f x T x f n n ∈-≤-这也就是说, )(x T n 是逼近 )(x f 的最佳 n 次多项式. 存在 在以后的应用中, 公式 (3) 中的 x 0 常被取作 0, 形式 ()'(0)(0)()(0)()1!!n n nf f f x f x x o x n =++++).(!)0(0)(nnk k k x o x k f +=∑=变为此式称为(带有佩亚诺型余项)的麦克劳林公式.泰勒( Taylor,B. 1685-1731, 英国 )麦克劳林( Maclaurin,C. 1698-1746, 苏格兰 )例1 验证下列公式2e 1();1!2!1.!nxn x xx o x n =+++++32112sin (1)();3!(21.)2!m m mxx x x o x m --=-++-+-2221cos 1(1)();2!(2)!3.mm m xx x o x m +=-++-+231ln(1)(1)();234.nn nx xx x x o x n-+=-+++-+211(6..)1nnx x x o x x=+++++-以上这些公式均为最基本的泰勒公式(麦克劳林公 2(1)(1)152!.x x x αααα-+=++++);(!)1()1(nn x o x n n ++--ααα 式), 请务必牢记.下面验证 1 和 6, 其余请读者自己验证.于是 e 的xn 阶麦克劳林公式为).(!!2!11e 2nnxx o n x x x +++++= 验证 1 因为 ,e )()(xk x f=所以.1)0()0()0()(==='=n ff f 2e 1();1!2!1.!nxnx x x o x n =+++++211(6..)1n nx x x o x x=+++++-,)1(!1)(2x x g -=',,)1(!2)(3 x x g -=''故101x n x=-于是在的阶麦克劳林公式为,)1(!)(1)(+-=n n x n x g).(1112nn x o x x x x+++++=- 验证 6 设 ,11)(xx g -=则 ,1)0(=g ,!1)0(='g ,!2)0(=''g ()!.)0(,n g n =例2 求 22()ex f x -=的麦克劳林公式, 并求 )0()98(f解 由例1 2e 1(),1!2!!nxnx x x o x n =+++++那么 2224222e 1(1)().222!2!x nn nn x x x o x n -=-+++-+⋅⋅.)0()99(f与,!492)1(!9814949)98(⋅-=f 由定理 6.8 的注 2, 可知上式就是 22ex -的麦克劳林 公式, ,0)0(!991)99(=f 于是得到 .0)0(,!492!98)0()99(49)98(=⋅-=ff由泰勒系数公式可知 9899x x 和的系数为x 1例3 求 在点 1=x 的泰勒公式.解 )1(111-+=x x 21(1)(1)x x =--+-+(1)(1)((1)).n n nx o x +--+-)]1([11---=x 下面这个例题是说明如何利用泰勒公式来求极限.211().1n nx x x o x x利用=+++++-例4 求 22330ln(1)e sin 1lim .x x x x x-→---+解 因为 ),(2)1ln(4422x o x x x +--=-4224e 1(),2!x x x o x -=-++333sin (),x x o x =+所以 22330ln(1)e sin 1lim x x x x x-→---+3330()lim 1.x x o x x→-+==-本题虽然可用洛必达法则来求, 但上法比较简单 .22333011()=lim x x x x o x x→--+-++前面讲的带有佩亚诺型余项的泰勒公式实际上是 0(()).no x x 下面是一个定量形式的泰勒公式.我们用泰勒多项式去替代函数,其误差为有限增量公式的一个推广, 泰勒公式带有拉格朗日型余项的 它只是定性地的告诉定理6.10(泰勒定理)若函数 ],[)(b a x f 在上存在直 在(a ,b )内存在(n +1)阶导数, 200000()()()()()()1!2!f x f x f x f x x x x x '''=+-+-+()(1)100()()(),(5)!(1)!n n n f x f x x n n ξ++++-+或者 (1)10()()()().(1)!n n n f f x T x x x n ξ++=+-+其中 n x x f x T n 的在点是0)()(阶泰勒多项式.到n 阶连续导函数, 0,[,],x x a b ∀∈则对(,),a b ξ∈存在使证 设 2()()()()[()()()1!2!f t f t F t f x f t x t x t '''=-+-+-;])(!)()(n n t x n t f -++ ,)()(1+-=n t x t G ),(0x x 上可导, 且0()(1)()0,[,).n G t n x t t x x '=-+-≠∈不妨设 ,0x x >上连续, 0(),()[,]F t G t x x 则在在 (1)00()()().(1)!n f F x G x n ξ+=+只要证明 (1)()()(),!n n f t F t x t n +'=--()()0F x G x ==由柯西中值定理(1)0,(),()(,),(1)!n f x x a b n ξξ+=∈⊂+于是得到 (1)10()()()().(1)!n n n f f x T x x x n ξ++=+-+我们称(1)10()()()()()(1)!n n n n f R x f x T x x x n ξ++=-=-+0000()()()().()()()()F x F x F x FG x G x G x G ξξ'-=='-为 f (x ) 在点 x 0 的 n 阶拉格朗日型余项.称为 f (x ) 在点 x 0 的带有拉格朗日型余项的 n 阶 注 请比较公式 (5) 与拉格朗日中值定理.泰勒公式. 故存在正数 (01),θθ<<使得 ,)(00x x x -+=θξ所以 )(x R n 又可写成.)()!1())(()(1000)1(++-+-+=n n n x x n x x x f x R θ因 0x x ξ介于与之间, 200000()()()()()()1!2!f x f x f x f x x x x x '''=+-+-+()(1)100()()(),(5)!(1)!n n n f x f x x n n ξ++++-+当 00=x 时, 公式 (5) 成为2(0)(0)()(0)1!2!f f f x f x x '''=+++()(1)1(0)().(6)!(1)!n n n n f f x x x n n θ+++++公式 (6) 称为带有拉格朗日型余项的麦克劳林公式. 样. 为泰勒多项式, 公式 (3) 与公式 (5) 都是泰勒公式, 并且前面部分均 余项.而不同的是 R n (x ) 的表达形式不一 读者在应用时,需根据不同情况选择合适形式的例1 中六个公式的余项均为佩亚诺型的, 现在将 它们改写为带有拉格朗日型余项的公式:21e e 1,2!!(1)(!i)n x x n x x x x n n θ+=++++++(01,(,)).x θ<<∈-∞+∞3211sin (1)3!(1!i )2(i )m m x x x x m --=-++--21cos (1),(01,(,)).(21)!m m x x x m θθ++-<<∈-∞+∞+242cos 1(1)2!4!(2)!(iii)m m x x x x m =-+++-,)!22(cos )1(221+++-+m m x m x θ(01,(,)).x θ<<∈-∞+∞1ln(1)(1)3(iv)2n x x x x x n-+=-+++-11(1),(1)(1)n n n x n x θ+++-++(01,1).x θ<<>-2(1)(1)(12!v)x x x αααα-+=+++n x n n !)1()1(+--+ααα (01,1).x θ<<>-11(1)()(1),(1)!n n n x x n ααααθ--+--+++2211,1(1)(vi)n n x x x x x x θ+=+++++--(01,1).x θ<<>-这里仅对公式 (iii) 进行验证, 其余 5 个请读者自证. 于是(0)1,(0)0,(0)1,(0)0,f f f f ''''''===-=()cos ,f x x =设则0,1,2,.k =()π()cos(),2k f x x k =+⋅,)1()0()2(m m f -=(22)1()cos((1))(1)cos .m m f x x m x θθπθ++=++=-,0)0()12(=+m f从而有)!2()1(!4!21cos 242m x x x x mm -+++-= 122(1)cos .(21)!m m x x m θ++-+⋅+例5 (1) 计算 e 的值,使其误差不超过 .106-(2) 证明 e 是无理数.解 由例5 可知11e e 11,0 1.2!!(1)!n n θθ=+++++<<+所以误差因为,3e 2,10<<<<θ6933(1)10.10!3628800R -<=<泰勒公式在近似计算中的应用于是 11e 2 2.718281,2!9!≈+++≈其误差不超过 .610-11e !e !(11).(7)2!!1n n n n θ-++++=+e (,)1.p p q q ==倘若是有理数下证 e 是无理数. 这是因为矛盾. ( 同样可证明 都不是有理数.)sin1,cos1,则 (7) 式左边是整数, 当n >2时(7)式右边不是整数. 3,n q n ≥≥取且e e 3,111n n n θ<<+++由于 所以 e 是一个无理数.例 6 计算 ln2 的值, 使其误差不超过10 -4.解 我们自然会想到利用公式 (iv),此时用 x = 1 代入,它的余项是11(1)(1),0 1.(1)(1)n n n R n θθ+=-<<++现考虑函数.11,11ln )(<<--+=x xx x f (1)0.0001,10000.R n <>要确保必须满足显然这样的计算量太大, 所以必须寻找新的方法. 阶泰勒多项式为:的因为n x )1ln(+21(1),2n nx x x n---++阶泰勒多项式为:的n x )1ln(-2,2n x x x n ----1ln 21x n x +-所以的阶泰勒多项式为:.1232123⎪⎪⎭⎫ ⎝⎛-+++-n x x x n 而 1212)12()1()!2()1()!2()(----+-++=n n n x n x n x f ,)1()!2()1()!2(1212++-++=n n x n x n于是.)1(1)1(1121)(1212122+++⎥⎦⎤⎢⎣⎡-+++=n n n n x x x n x R θθ112,. 13x x x +==-令解得221110.0001,3212n n R n ⎛⎫⎛⎫≤< ⎪ ⎪+⎝⎭⎝⎭只要取 n = 6, 便得到311111ln 220.6931,333113⎛⎫≈+++= ⎪⨯⨯⎝⎭其误差不超过0.0001 (真值为0.693147180…). 要使复习思考题阶泰勒多项式,的在是若n x x f x T n 0)()(.1 2. 7?教材上的例说明了什么那么,在什么条件下 T n (x 2) 一定是 f (x 2) 的 2n 阶 泰勒多项式?。