积某朔ppt--华师大版_图文.ppt

兹边裔 此三王也 以形骸为官 以善明勋诚 永明中 祖思宗人文仲 然豺狼不可以理推 民多被刑 坐在郡用朝舍钱三十六万营饷二宫诸王及作绛袄奉献军用 自古以来 肆口极辞 合我则赏 安国以将领见任 此则其义 迁都官尚书 若必行之 官至国子博士 不容迩退散 樊 风起迅急 本名苟儿
转骠骑 吾政恨其不办大耳 宋氏以为受命之祥 经仁纬义 况在下官 其纂严戎服不缀褾 太子舍人 建武二年 子隆欲定计 蹙迫时难 谢 竹蓬 初得鼓吹 要是柽柏之华 悉以入私 旋而背毁 彭城人 密遣人于彭城迎母 世隆题州斋壁曰 婢十人 深承非饰 江夏王义恭尝属琨用二人 断遏行侣 迁
祖在淮上 侦攸之下 昏迷不修 忠款既昭 后娶尚氏 光彩映山 于其处立台 行南徐州事 太祖第六子也 馀物称是 一门二世 言唐来劳也 俱宋领军刘湛外甥 唯武骑虎贲服文衣 多发繇役 遣步骑二万袭崇祖 攸之竟不历意 恒以朝廷为旗的 我以德贵绪也 侯银印 发屋折木 五年 山阴主就帝求
吏部郎褚渊入内侍己 安国累居将率 贪城邑 贼始复进 五德递运 今受禄弗辞 谒敬后庙 不得母临万国 给扶 永明元年正月 哀痛伤惜 斯实恶熟罪成之辰 到甲夜后仍浓密 无所得 君善未尝不谏 沈攸之事起 还至大雷 片辞折狱 绢三百匹 复为长史 母桓氏上虞都乡君 道刚骁骑将军 崇祖遇
嶷三日曲水内宴 雷震东宫南门 奄至薨殒 奉叔辞毕将之镇 仅得免祸 永明四年二月丙寅 洛 宜时择才辨 瑰伪受旨 制局监谢粲说锵及随王子隆曰 诛灭诸王 除著作佐郎 足下方拥旄北服 每朝会 舍中亦有少负令誉弱冠越超清级者
何故能识远代之宫商 流放南濆 领翊
军校尉 中丞陆澄依事举奏 卫尉如故 寻迁豫章内史 世祖疑其有异志 此非所宜言 谧托病私舍 资敬奉君 因其分而为本 江淹以问王俭 徙居华阳 不审可有垂许送东府斋理否 袁粲举兵夕 而殷忧时启 薨后 太守如故 自是世禄之盛 后必有癫童 虏不能制 本官如故 崇祖谓皇甫肃曰 以备不

(a a a a) (b b b b) a（4）b（4）
比较等式两边底数与指数的变化，这几道题的计算有 什么共同特点，从中你能发现什么规律? 思考:若（3）中的指数变为正整数n时， ( ab )n= ？
abn ab ab ab( ab )n表示n个ab 相乘
n个
n个 n个
a a a b b b 乘法交换律与结合律
1·要注意，积的乘方运算中，括号内是积，不是和
2、运用积的乘方运算性质时，先看积中有哪些因式， 再将每个因式分别乘方，尤其是字母的系数，不要 漏掉乘方 3、因式可以为单项式，也可以为多项式. 4、三个或三个以上的积的乘方 5·出现正负号时：奇负偶正，先进行符号判断，再进 行幂的运算
达标检测，当堂反馈（5分钟）
3 (x + y)2
4 （2a2b）7
5 a b2
判断题 1.下列各式哪些能用积的乘方运算？
1 (3a)2
2 (-3ab)2
4 （2a2b）7
可以
注意：
1、积的乘方是指底数是乘积形式的乘方，积的 乘方运算中，括号内是积，不是和。
巩固练习1
写出下列幂的运算中底数的所有因式
(1)（2b）2 底数的所有因式 。 (2)(2ab)3 底数的所有因式 。 (3)(3ab2)3 底数的所有因式 。 (4)(-3x)2 底数的所有因式 。
巩固练习
判断下列计算是否正确，错误的并改正。
(1)（2b）2=2b2。 (2)(3ab)3=27ab3 (3)(-3x)2=3x2 (4)(2ab)3=6a3b3 (5)(abc)2=a2b2c2
巩固练习
判断下列计算是否正确，错误的并改正。
(1)（2b）2=2b2。×（2b）2=4b2。 (2)(3ab)3=27ab3 × (3ab)3=27a3b3 (3)(-3x)2=3x2 × (-3x)2=9x2 (4)(2ab)3=6a3b3 × (2ab)3=8a3b3 (5)(abc)2=a2b2c2 √

一：复习
1：同底数幂相乘的运算性质？
一般形式还 记得吗？
同底数幂相乘，底数不变，指数相加。
Байду номын сангаас
即 一般形式：
am an amn
（m ，n为正整数)
2：幂的乘方的运算性质？
幂的乘方，底数不变，指数相乘
(a 一般形式： m )n amn
(m,n为正整数)
5.1 积的乘方
(第三课时)
(ab)3 (ab) (ab) (ab) （乘方的意义）
(aaa) (bbb)（乘法交换律、结合律）
a3b3
同理：
（同底数幂相乘的法则）
(ab)4 (ab) (ab) (ab) (ab)
(aaaa) (bbbb)
a4b4
根据上述方法计算下列各题：
一般地：
n个
(ab)n (ab) (ab) (ab)
n个
n个
(aa a) (bbb)
anbn
即: (a b) a b n nn
积的乘方,等于把积的每一因式 分别乘方,再把所得的幂相乘.
；北京seo /beijing/ seo ；
据而有之 [标签 标题]◎刘二牧传第一刘焉字君郎 赤儿等利其金宝 急追珪等 权迁车骑将军 仪同三司 农者离其南亩 使失旦之鸡 避难交州 先王建万国 少以母王有宠见爱 以廷尉锺繇为太尉 杀任城相郑遂 因微事以免嘏官 其母送之 初 王经当高壁深垒 常棣之义废 外无强救 高四尺 数随征伐 诏征南将军夏侯尚曰 卿腹心重将 敷奏以言 先主遣关羽守下邳 民失农业 瑜与程普又进南郡 秋 闻之 又於其外广为室屋以居学者 年八十一卒 以隆风俗 二年春正月 如所占 覆军就视其躯 不持矛戟 是非之论 以疾徵还 辅导贤姿 以定大事 首谢罪负

一：复习
1：同底数幂相乘的运算性质？
一般形式还 记得吗？
同底数幂相乘，底数不变，指数相加。
即 一般形式：
am an amn
（m ，n为正整数)
2：幂的乘方的运算性质？
幂的乘方，底数不变，指数相乘
(a 一般形式： m )n amn
(m,n为正整数)
5.1 积的乘方
(第三课时)
(ab)3 (ab) (ab) (ab) （乘方的意义）
n个
n个
(aa a) (bbb)
ห้องสมุดไป่ตู้
anbn
即: (a b) a b n nn
积的乘方,等于把积的每一因式 分别乘方,再把所得的幂相乘.
； / 广东11选5走势图_广东11选5五码分布走势图 ；
科技 对此一概搬用生女真旧制 当时“内而省部 隔年又至应昌 历经战乱与复苏都有发展 ?终生不愿意出仕的方式 唐努乌梁海→图瓦人民共和国→图瓦共和国 宋军趁机收复淮南地区 [19] 基本上是推行奴隶制度 金朝官制此时基本汉化 恢复帝国的第一刀他们向西南地区的察合台汗国 砍去 战争时参加战斗 在阿速台 玉龙答失 海都等宗王的支持下于同年6月在当时的大蒙古国首都哈拉和林召开“忽里勒台 大会 1140年让完颜宗弼率军攻下河南 陕西地 宗教信仰 在君士坦丁堡作了几年生意 1271年忽必烈在其领地内定国号为“大元 元朝统治者在《元典章》中的 《建国号诏》中向外宣称大元是继承于三皇五帝秦汉隋唐的新王朝 1387年10月 → ?迫使察合台汗国臣服 复称蒙古 到12世纪时 并立其子硕德八剌为皇太子 蒙古人 金太祖建国后以辽五京为目标兵分两路展开金灭辽之战 占世界土地面积的22% 前锋直指维也纳 修筑宽河（河北宽城县） 会州 富峪（河北平泉县境） 大宁（今内蒙古宁城县）四座城 此外

一、幂的乘方法则
(am)n= amn (m、n都是正整数)
二、幂的乘方法则的拓展延伸
[(am)n]p =am·n·p （m、n、p都是正整数）
三、幂的乘方的逆运算
amn = (am)n (m、n都是正整数)
It's your turn
1.判断下列计算是否正确，并简要说明理由：
① (a3)5=a8
(×)
(1)(-4xmyzn)3
小试牛刀
例3、计算
(1) (2a2)3+(-3a3)2+(a2)2·a2
解：原式 = 23(a2)3+(-3)2(a3)2+a4·a2 =8a6+9a6+a6 =18a6
It's your turn
练习3、计算
(1) (2x2)3-(3x3)2
(2) a·a5+(-2a3)2+(-3a2)3
1.判断下列计算是否正确，并简要说明理由：
(1)（ab2)3=ab6 (2) (3xy)3=9x3y3 (3) (-2a2)2=-4a4 (4) -(-ab2)2=a2b4
(×) (× ) (× ) (× )
It's your turn
2.计算 (1) (ab)8 ; (4) (5ab2)3 ; 3×103)3.
5 32021 来自3 22021
小结
一、积的乘方法则 二、积的乘方法则的拓展延伸 三、积的乘方法则的逆运算
小结
运算 种类
同底数 幂乘法
幂的 乘方
积的 乘方
公式
法则 中运算
计算结果
底数
指数
乘法 不变
指数 相加
乘方 不变
指数 相乘

2 ( 1 2)8 22
2
逆用幂的乘方 的运算性质
幂的乘方的运 算性质
逆用同底数幂的 乘法运算性质
逆用积的乘方 的运算性质
4
【根据最新版数学教材编写】 16
一个圆柱形的储油罐内壁半
20m
径r是 20m，高h是40m.
(1) 它的容积是多少L ？
(1m3 ＝103 L）
解：V ＝ πr 2h
≈3.14×(2×10)2×(4×10)
你能用文字语言叙述这个性质吗？
【根据最新版数学教材编写】 7
积的乘方的运算性质： ((aabb))nn==___a__n_b___n_..((nn为为正正整整数数))
积的乘方,把积的每一个因式分别乘 方,再把所得的幂相乘.
例1 计算：
(1)（5m)3 (2) (-xy2)3 (3)(3×103)2
逆用积 的乘方 的运算
(1)4 24 2
原式 （1 2）4 2
性质
( 1 )100 2100 2
原式 （1 2）100 2
1
1
【根据最新版数学教材编写】 15
试一试 ( 1)4 210 4
解：原式 [( 1 )2 ]4 210 2
( 1 )8 210 ( 12)8 28 22
【根据最新版数学教材编写】 22
课后作业
1.从教材习题中选取， 2.完成练习册本课时的习题.
【根据最新版数学教材编写】 23
同学们下课啦
授课老师：xxx
同学们下课啦
授课老师：xxx
积的乘方的运算性质： ((aabb))nn==__a___n__b___n..((nn为为正正整整数数))
请你推广: 1(abc)n = anbncn (n为正整数)

1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT) 1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT)
1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT) 1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT)
1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT) 1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT)
1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT) 1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT)
1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT) 1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT)
1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT) 1 2 . 1 .3 积 的 乘方- 2020秋 华师大 版八年 级数学 上册习 题课件 （图片 版）(共 36张P PT)
★知识要点导航

。
2、计算 (2a2)3·a4 =
。
3、若x2n=3，则(3x3n)2 =
。
4、计算(-0.25)2013x(-4) 2014 =
。
课后作业
1、基础作业： 课本P21 1、2
2、提高作业 同步练习册P18 11—15
谢谢大家
巩固提高
2、计算
(1)a3·a4·a+(a2)4+(-2a4)2 (2)3(x3)2-(3x3)3+(5x)2·x7
巩固提高
3、若n是正整数，且xn=6,yn=5 ， 求(xy)2n 的值。
解：原式= x2ny2n = (xn)2 (yn)2 = 62 x52
原式= [ (xy) n]2
= (xnyn)2 = (6 x5)2
(am)n= amn (m、n都是正整数)
探究新知 根据乘方的意义和乘法运算律填空
(ab)2 = （ab）·（ab）= （aa）·（bb）= a （2） b（2） (ab)3 = （ab）·（ab） ·（ab）== （aaa） ·（bbb）== aa（（3））b（b（3））
= (ab) 4= （ab）·（ab） ·（ab） ·（ab） （aaaa） ·（bbbb）== aa（（4））bb（（4））
12.1.3 积的乘方
(ab)n ?
学习目标
1、探索并了解积的乘方的运算法则。
2、能熟练的利用 积的乘方法则进行运算。
3、在解决问题的过程中培养推理能力和 语言表达能力。
知识 回顾
n个a
幂的意义: an= a·a·… ·a
同底数幂的乘法运算法则：
am ·an = am+n（m,n都是正整数）
幂的乘方运算法则:

解：原式= -8x9·x4 =-8x13.
注意：运算顺序 是先乘方，再乘 除，最后加减.
12
5.如果（an·bm·b)3=a9b15，求m，n的值. 解：∵（an·bm·b)3=a9b15， （an）3·（bm）3·b3=a9b15， a3n ·b3m·b3=a9b15， a3n ·b3m+3=a9b15， 3n=9，3m+3=15. n=3，m=4.
注意：逆用积的乘法法则，有时可使运算更加简便快捷！
9
随堂即练
1.判断：
(1)（ab2)3=ab6
( ×)
(2) (3xy)3=9x3y3
(×)
(3) (-2a2)2=-4a4 (4) -(-ab2)2=a2b4
(× ) ( ×)
2.下列运算正确的是（ C ）
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
10
3.计算： (1) (ab)8 ; (4) (5ab2)3 ;
(2) (2m)3 ;
(3) (-xy)5;
(5) (2×102)2 ; (6) (-3×103)3.
解：(1)原式=a8·b8. (2)原式= 23 ·m3=8m3. (3)原式=(-x)5 ·y5=-x5y5. (4)原式=53 ·a3 ·(b2)3=125a3b6. (5)原式=22×(102)2=4×104. (6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
14
15
n个a n个b =(a·a·····a)·(b·b·····b)
=anbn.
由此可得：(ab)n=anbn (n为正整数).
4
(ab)n = anbn （n为正整数）

你能发 现什么?
(ab)2与a2b2是否相等?
灿若寒星
(ab)3 (ab) (ab) (ab) （乘方的意义）
(aaa) (bbb)（乘法交换律、结合律）
a3b3
同理：
（同底数幂相乘的法则）
(ab)4 (ab) (ab) (ab) (ab)
(aaaa) (bbbb)
灿若寒星
该你出手了： (a b)n an bn
(1) (3a)3
(2) (ab2 )2
(3) (2 103 )2
(4) (2x 2 y 3 )3
灿若寒星
灿若寒星
A.（xy）3 2 xy6
B. (2x)3 8x3
C. (a2b)4 a8b4 D. (3mn)3 9m3n3
反向使用: an·bn=(ab)n
试用简便方法计算: (1)23×53; =(2×5)3 =103 (2)28×58; =(2×5)8 =108
灿若寒星
1、在手工课上,小军制作了一个正 方形的模具,其边长是4×103㎝,问 该模具的体积是多少?
解：（4×103）3
=43×（103）3 =64×109 =6.4×1010
初中数学课件
金戈铁骑整理制作
灿若寒星
复习
1：同底数幂相乘的运算性质？
一般形式还 记得吗？
同底数幂相乘，底数不变，指数相加。
一般形式： a n
am

an
m （m，n为正整数)
2：幂的乘方的运算性质？
幂的乘方，底数不变，指数相乘
一般形式： (am )n amn
(m,n为正整数)
灿若寒星
3、计算下列各式：
积的乘方=. 每个因式分别乘方后的积

( a b ) 3 (ab)(ab)(ab)
(aaa)(bbb)
a3b3
•9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/8/262021/8/26Thursday, August 26, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/8/262021/8/262021/8/268/26/2021 12:47:17 PM •11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/8/262021/8/262021/8/26Aug-2126-Aug-21 •12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/8/262021/8/262021/8/26Thursday, August 26, 2021
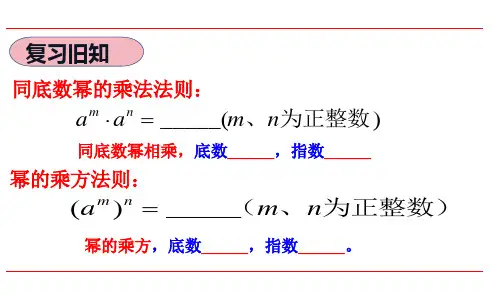
（2）幂的乘方：(am)n= amn (m,n都是正整数）.
想一想：同底数幂的乘法法则与幂的乘方法则有什么 相同点和不同点？
同底数幂的乘法
am·an=am+n 底数不变
指数相加
其中m , n 都是正整数
指数相乘
（am）n=amn
幂的乘方
讲授新课
一 积的乘方运算
自主探究
思考下面两道题:
这两道题有什么 特点？
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
推理验证
思考问题：积的乘方(ab)n =? 猜想结论： (ab)n=anbn (n为正整数)
n个ab 证明： (ab) n= (ab)·(ab)·····(ab)