(精品)小学二年级数学加减巧算大全
- 格式:pdf
- 大小:149.02 KB
- 文档页数:10


二年级速算方法与技巧口诀
1. 加法凑十法呀,那可太好用啦!比如 8+5,把 5 分成 2 和 3,8 和 2 凑成 10,再加上 3 就是 13 啦!这方法多棒呀,你说是不是?
2. 减法破十法也很厉害哟!像 13 减 5,把 13 分成 10 和 3,10 减 5 等于 5,再加上 3 就是 8 呀!这不是很简单嘛?
3. 个位相同的数相加,有个小窍门哦!5+5 等于 10,那 25 加 35 呢,个位 5 加 5 等于 10,十位 2 加 3 等于 5,不就是 60 嘛!你试试看呀!
4. 十几减几,用个小技巧就轻松搞定啦!12 减 3,把 12 分成 10 和2,10 减 3 等于 7,再加上 2 就是 9 啦!是不是很神奇呀?
5. 乘法也有口诀哦,一一得一,一二得二,这多顺溜呀!就像 2 个 3 就是 6 呀,简单吧!
6. 除法也不难呀,20 除以 5 等于 4,就好像把 20 个糖果平均分给 5 个小朋友,每个小朋友得 4 个呀,这很好理解吧!
7. 加减混合运算,先算前面的呀!比如 3+5-2,先算 3 加 5 等于 8,再算 8 减 2 等于 6 啦,很容易的哟!
8. 乘法的交换律也好用呢!2 乘以 3 等于 3 乘以 2 呀,都是 6 呢!这多有意思呀!
9. 看到数字就想想口诀呀,这能让你算得又快又准呢!就像看到 3 个4,马上就想到三四十二呀!
10. 算来算去,技巧用对了就简单啦!平时多练练,速度就上来啦!加油哦!
我的观点结论:这些速算方法和技巧口诀真的很实用,能让二年级的小朋友们算得更快更准,一定要好好掌握呀!。

二年级加减法简便运算二年级简便运算一、加法凑整例:112+36+28=176+28=204例:215+37+23=215+60=275口算练:82+73+18=173+18=19135+36+25=71+25=9619+23+17=42+17=5938+13+62=51+62=11318+56+24=74+24=9831+27+33=58+33=9126+37+24=63+24=8771+32+68=103+68=171 61+32+29=93+29=12298+44+32=142+32=174 15+21+39=36+39=7524+33+46=57+46=10335+46+14+25=81+39=120 36+47+14+23=83+37=12078+29+12+11=107+23=13032+67+23+58=99+81=18088+24+16+12=112+28=14055+39+25+21=94+46=140解决问题:1、XXX有25张画片,照片比画片多18张。
照片和画片一共多少张?答:25+25+18=68(张)2、水果店运来一批苹果,上午卖出26筐,下午卖出38筐,还剩12筐.运来多少筐?答:运来的筐数为:26+38+12=76(筐)二、减法凑整例:192-26-32=140-32=108 简便运算:63-34-13=63-47=1687-25-47=87-72=1572-19-52=72-71=1口算练:91-45-21=46-21=2584-29-44=55-44=1168-36-18=32-18=1489-25-59=64-59=565-38-25=27-25=296-47-36=49-36=1380-13-50=67-50=1773-26-33=47-33=1487-48-17=39-17=22解决问题:1、果园里有73棵树,苹果树有26棵,杏树有33棵。
其余的是桃树,桃树有多少棵?答:73-26-33=14(棵)2、一本书有98页,第一天看了35页,第二天看了28页,要把这本书看完,第三天要看几页?答:第一天和第二天看了63页,还剩35页。

二年级数学巧算100题一、加法巧算1. 25 + 36 + 15- 解析:观察式子可以发现25和15相加能凑成整十数。
所以先算25 +15=40,再算40+36 = 76。
2. 18+23+32- 解析:18和32相加可得整十数,先计算18 + 32 = 50,再算50+23=73。
3. 34+19+26- 解析:34和26相加为60,然后60 + 19=79。
4. 12+38+29- 解析:先算12+38 = 50,再算50+29 = 79。
5. 45+17+15- 解析:45和15相加得60,60+17 = 77。
二、减法巧算6. 85 - 36 - 14- 解析:36和14相加可凑成50,根据减法的性质,一个数连续减去两个数等于这个数减去这两个数的和。
所以85-(36 + 14)=85 - 50=35。
7. 92-27-23- 解析:27和23相加得50,92-(27 + 23)=92 - 50 = 42。
8. 76-18-22- 解析:18和22相加是40,76-(18+22)=76 - 40 = 36。
9. 65-29-11- 解析:29和11相加为40,65-(29+11)=65 - 40 = 25。
10. 58 - 17 - 23- 解析:17和23相加得40,58-(17 + 23)=58 - 40 = 18。
三、加减混合巧算11. 32+28 - 12- 解析:先算32+28 = 60,再算60 - 12 = 48。
12. 45 - 18+15- 解析:先算45+15 = 60,再算60 - 18 = 42。
13. 23+37 - 13- 解析:先算23 - 13 = 10,再算10+37 = 47。
14. 56+14 - 26- 解析:先算56 - 26 = 30,再算30+14 = 44。
15. 38 - 19+22- 解析:先算38+22 = 60,再算60 - 19 = 41。

二年级数学巧算100题(10篇)我们总是觉得数学是一门很枯燥、没有精彩点的学科。
其实不然,如果我们深入了解数学、研究数学你就会发现里面也有十分有趣的地方。
昨天,妈妈下班回家给我看了一个有趣的信息,信息里是一些阿拉伯数字组成的金字塔一样的题目,看了这些奇妙的数字,我不由得赞叹不已,就这些简单的数字竟能拼成这么完美的形状出来。
然后妈妈选了一组来给我做题,说要让我亲自做做题目,自己感受一下它的奇妙。
题目是:1×9+2=?、12×9+3=?、123×9+4=?、1234×9+5=?以此类推一直到×9+10=?;我看到这些题目就说:“这也没什么特别奇妙的啊。
”妈妈听到就说:“那好,我们把它竖起来写。
”哈哈,这个题目就有趣多吧,然后我就拿起笔开始计算起来了,刚算了两题就把我难住了,妈妈看到我为难的样子,就从身后拿出了计算机说到:“我知道四年级的小朋友还没教到3位数以上的乘法,但是今天我们不是来做算数题目的,我们是来体验数学的奇妙的,来,下面的题目就用计算机算吧。
”我迫不及待的拿过计算机“啪啪啪”的按着计算机上的按钮开始计算了。
当我开始计算第6题时,妈妈一把拿走计算机:“接下来4道题你自己充分发挥现象来做吧,这下我傻眼了:“个、十、百、千、万、十万、十万位的数字叫我怎么算啊?”我心里正纳闷着,妈妈看到我为难的样子就笑了:“欣芸看看上面5道题的得数有什么规律啊?”我刚才只顾着计算题目,还没注意到呢,结果一看,傻眼了,怎么都是1啊?而且一道比一道多一个1。
妈妈接着补充说到:“先看看每道题的规律,然后结合规律、充分发挥现象来做题喔。
”我发现每道题前面多加一位数,后面的得数也就会多出一个1来,这个会不会就是解题的规律呢?我半信半疑地按着这个规律做完了后面的题目,做完之后,我赶紧用计算机检查了一遍,得数居然都是对的,我的心里美滋滋的。
今天数学小测试,我认真地答题,仔细地计算,字迹也比较工整。

二年级学而思巧算.————————————————————————————————作者:————————————————————————————————日期:加减法的速算与巧算一、凑整法:两个数相加,若能恰好凑成整十、整百、整千、整万…,就说两个数互为“补数”。
10 =1.计算:(1)32+17+48 (2)53+36+47 (3)24+44+56 (4)389+163+237 (5)223+168+332 (6)478+243+222 2.计算(拆分凑整):(1)96+15 (2)52+69 (3)63+18+19 (4)28+28+28 (5)574+498(6)1003+103+13+3二、减法中的巧算1.把几个互为“补数”的减数先加起来,再从被减数中减去。
(1)500-75-25 (2)1000-370-3302.先减去那些与被减数有相同尾数的减数。
(1)566-338-166 (2)843-122-543三、混合运算改变运算顺序:在只有“+”、“—”号的混合算式中,运算顺序可改变※带着符号搬家1.计算:(1)674+367-174(2)45-18+19(3)874-(379+274)+579 (4)356+(644-178)利用“补数”把接近整十、整百、整千…的数先变整,再运算(注意把多加的数再减去,把多减的数再加上)。
(1)506-397 (2)323-189(3)467+997 (4)987-178-222-390四、计算等差数列的和相邻的两个数的差都相等的一串数就叫等差连续数,又叫等差数列,如(1)1,2,3,4,5,6,7,8,9(2)1,3,5,7,9(3)2,4,6,8,10(4)3,6,9,12,15(5)4,8,12,16,20 等等都是等差连续数.1. 等差连续数的个数是奇数时,它们的和等于中间数乘以个数,简记成:和= 中间数×个数(1)计算:1+2+3+4+5+6+7+8+9=5×9 中间数是5 共9个数=45(2)计算:1+3+5+7+9 (3)计算:2+4+6+8+10(4)计算:3+6+9+12+15 (5)计算:4+8+12+16+20+24+28+32+362. 等差连续数的个数是偶数时,它们的和等于首数与末数之和乘以个数的一半,简记成:和=(首数+ 末数)×个数的一半(1)计算:1+2+3+4+5+6+7+8=(1+8)×4=9×4 首+ 末是9 个数的一半是4=36(2)计算:3+5+7+9+11+13+15+17(3)计算:6+8+10+12+14+16+18+20+22+243.计算:(1)1+2+3+4+5+6+7+6+5+4+3+2+1(2)1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2 +1(3)1+2+3+4+5+6+7+8+7+6+5+4+3五、基准数法:各加数大小都接近某整十整百的数。

二年级巧算练习题加减3.135+75-35+254.7845.739+141-639-41 .8867.1996-.1326+39-184+61 -26-74-8--629.9+99+999+999 10.298+996+995+1111.1465-386+3812.702113.1005-201-394-206-19914.1968-101+398-297-95-40515.12+14+16+18+20+22+24+26+28-284+28116.1 = 17.1 =418.1 = 19.1 =820.1 =121.122.24.=1 3. =425. ===加减法的巧算例题1 计算3326+303574+49方法一:先看做整十,整百,整千的数进行计算。
3326+3074+498=3326+300+=574+500-2=3626+ =1074-2=362=1072方法二:根据“和”的变化规律:一个加数增加多少,另一个加数就减少多少,那么和不变,来进行简算。
3326+3074+498=+ =+=3329+300=572+500=362=1072特别注意:在计算时,将接近整十,整百,整千的数看成整十,整百,整千的数进行计算,然后根据和不变的规律,多加的要减掉,少加的要补上。
例题计算487+321+113+479方法:487和113,321和479分别可以凑成整百数。
我们可以通过交换位置的方法,487+113得600,321+479得800.487+321+113+479=+=600+800=1400特别注意:这道题要运用凑整的思路,将487和113,321和479分别凑成整百数,便于计算。
注意:先算的要加括号。
例题计算 998+998+98+8方法:本题可采用凑整的方法,将9998,998,98分别凑成10000,1000,100.而凑成这些数可从8里面借用。
9998+998+98+8=+++2= __________________________ =————————————特别注意: 对于接近整百,整千的数,应先将其凑成整数,然后再将多加的数从后面去掉。

二年级数学巧算加减法1. 凑整法。
- 加法凑整。
- 概念:在加法运算中,把两个或几个数凑成整十、整百、整千等的数,再进行计算会更简便。
- 例如:计算28 + 36,可以把28看成30 - 2,把36看成40 - 4。
- 那么28+36=(30 - 2)+(40 - 4)=30+40-(2 + 4)=70 - 6 = 64。
- 再如:19+31+22,可以先算19+31 = 50(因为19和31凑成整十数50),再算50+22 = 72。
- 减法凑整。
- 概念:在减法运算中,把减数凑成整十、整百、整千等的数,再进行计算。
- 例如:计算83 - 29,可以把29看成30 - 1。
- 那么83 - 29=83-(30 - 1)=83 - 30+1 = 53+1 = 54。
2. 带符号搬家法(交换律)- 在加减法混合运算中,可以带着数字前面的符号搬家。
- 例如:32+18 - 12,可以先算32 - 12+18。
- 先计算32 - 12 = 20,再算20+18 = 38。
- 再如:45 - 23+15,可以先算45+15 - 23。
- 45+15 = 60,60 - 23 = 37。
3. 添括号、去括号法(结合律)- 添括号。
- 如果括号前面是加号,添括号后里面的符号不变。
- 例如:25+13+7 = 25+(13 + 7)=25+20 = 45。
- 去括号。
- 如果括号前面是加号,去括号后里面的符号不变。
- 例如:36+(24 - 16)=36+24 - 16 = 60 - 16 = 44。
- 如果括号前面是减号,去括号后里面的符号要变号。
- 例如:50-(18+12)=50 - 18 - 12 = 32 - 12 = 20。
4. 基准数法。
- 当有多个数相加且这些数都接近某个数时,可以把这个数作为基准数。
- 例如:计算21+19+23+18+22。
- 可以把20作为基准数。
- 21 = 20+1,19 = 20 - 1,23 = 20+3,18 = 20 - 2,22 = 20+2。

小学数学二年级下册加减法巧算加法互换律两个或两个以上因数相加时 , 因数互换地点,和不变。
这个规律叫加法互换律此法也合用于有减法或加减法同时存在时用字母表示: A+ B= B+ A15+8= 8+ 15=23A+B+C=A+C+B15+9+5=15+5+9=20+9=29A+B-C=A-C+B13+8-3=13-3+8=18A-B-C=A-C-B84-27-14=84-14-27=70-27=43加法联合律三个数相加,能够先把前两个数相加,再加第三个数,或许先把后两个数相加,再与第一个数相加,它们的和不变。
这个规律叫加法联合律此法也合用于有减法或加减法同时存在时用字母表示: A+ B+ C= A+( B+ C) 18+25+15=18+(25+15)=18+40=58A+B-C=A+( B-C)18+25-15=18+(25-15)=18+10=28互换律和联合律并用A+B+C+D=A+C+B+D( 互换律 ) =(A+C)+(B+D)( 联合律 )例:18+23+32+47=18+32+23+47=(18+32)+(23+47)=50+70=120拆掉 () 1、当() 前为 +时,拆掉 () 时 () 内+,- 号不变A+(B+C)=A+B+C15+(8+25)=15+8+25=15+25+8=(15+25)+8=40+8=48A+(B-C)=A+B-C65+(33-25)=65+33-25=65-25+33=(65-25)+33=40+33=732、当() 前为 - 时,拆掉 () 时() 内 +,- 号要改变 A-(B+C)=A-B-C85-(8+25)=85-8-25=85-25-8=60-8=52 A-(B-C)=A-B+C65-(33-25)=65-33+25=65+25-33=90-33=57加 () 1、当加 () 时 () 前为 +时, () 内 +,- 号不变A+B+C=A+(B+C)8+15+25=8+(15+25)=8+40=48A+B-C=A+(B-C)65+33-23=65+(33-23)=65+10=752、当加 () 时() 前为 - 时, () 内+,- 号要改变A-B-C=A-(B+C)85-8-22=85-(8+22)=85-30=52A-(B-C)=A-B+C65-28+18=65-(28-18)=65-10=55综合例题 :97+(21+13)86+(43-26)+1722-(36-18)86-(29+26)-11=97+21+13=86+43-26+17=22-36+18=86-29-26-11=97+13+21=86-26+43+17=22+18-36=86-26-29-11=110+21=(86-26)+(43+17)=40-36=(86-26)-(29+11)=131=60+60=4=60-40=120=2036+87+6499+136+1011361+ 972+639+28300-73-271000-90-80-20-104723-(723+189)2356-159-256506-397-103323-189+77-11467+ 997987-178-222-390100 + (10-30)-70197+(221+13)186+(43-26)+17122-(236-178)。

小学数学二年级下册加减法巧算加法交换律两个或两个以上因数相加时,因数交换位置,和不变。
这个规律叫加法交换律此法也适用于有减法或加减法同时存在时用字母表示:A+B=B+A15+8=8+15=23A+B+C=A+C+B15+9+5=15+5+9=20+9=29A+B-C=A-C+B13+8-3=13-3+8=18A-B-C=A-C-B84-27-14=84-14-27=70-27=43加法结合律三个数相加,可以先把前两个数相加,再加第三个数,或者先把后两个数相加,再与第一个数相加,它们的和不变。
这个规律叫加法结合律此法也适用于有减法或加减法同时存在时用字母表示:A+B+C=A+(B+C)18+25+15=18+(25+15)=18+40=58A+B-C=A+(B-C)18+25-15=18+(25-15)=18+10=28交换律和结合律并用A+B+C+D=A+C+B+D(交换律)=(A+C)+(B+D)(结合律)例:18+23+32+47=18+32+23+47=(18+32)+(23+47)=50+70=120拆除()1、当()前为+时,拆除()时()内+,-号不变A+(B+C)=A+B+C15+(8+25)=15+8+25=15+25+8=(15+25)+8=40+8=48A+(B-C)=A+B-C65+(33-25)=65+33-25=65-25+33=(65-25)+33=40+33=732、当()前为-时,拆除()时()内+,-号要改变A-(B+C)=A-B-C85-(8+25)=85-8-25=85-25-8=60-8=52A-(B-C)=A-B+C65-(33-25)=65-33+25=65+25-33=90-33=57加()1、当加()时()前为+时,()内+,-号不变A+B+C=A+(B+C)8+15+25=8+(15+25)=8+40=48A+B-C=A+(B-C)65+33-23=65+(33-23)=65+10=752、当加()时()前为-时,()内+,-号要改变A-B-C=A-(B+C)85-8-22=85-(8+22)=85-30=52A-(B-C)=A-B+C65-28+18=65-(28-18)=65-10=55综合例题:97+(21+13)86+(43-26)+1722-(36-18)86-(29+26)-11=97+21+13=86+43-26+17=22-36+18=86-29-26-11=97+13+21=86-26+43+17=22+18-36=86-26-29-11=110+21=(86-26)+(43+17)=40-36=(86-26)-(29+11)=131=60+60=4=60-40=120=2036+87+6499+136+1011361+972+639+28300-73-271000-90-80-20-104723-(723+189)2356-159-256506-397-103323-189+77-11467+997987-178-222-390100+(10-30)-70197+(221+13)186+(43-26)+17122-(236-178)。
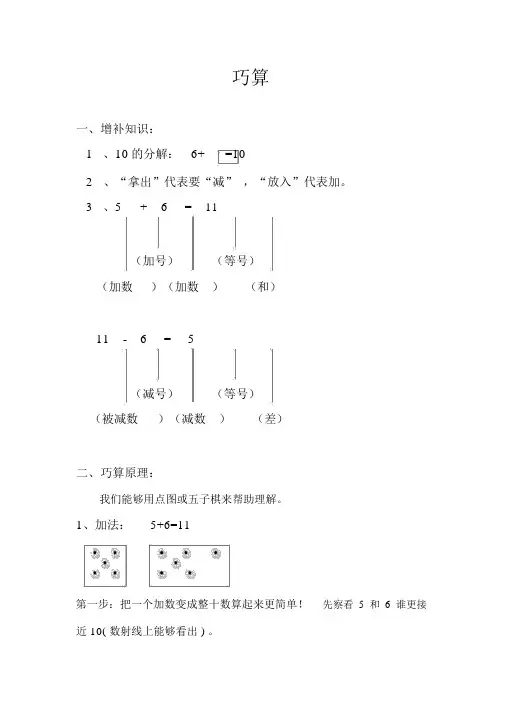
巧算一、增补知识:1、10的分解:6+ =102、“拿出”代表要“减” ,“放入”代表加。
3、5+ 6 =11(加号)(等号)(加数)(加数)(和)11 - 6 = 5(减号)(等号)(被减数)(减数)(差)二、巧算原理:我们能够用点图或五子棋来帮助理解。
1、加法:5+6=11第一步:把一个加数变成整十数算起来更简单!先察看5和6谁更接近 10( 数射线上能够看出 ) 。
第二步:我们从左侧的方框里拿出4个(5-4=1),放入右侧的方框里(6+4=10)。
左侧方框里还有1 个小圆点,右侧10 个,10+1=11。
一个加数增添,另一个加数减少同样的数,和不变。
2 、减法11-6=5把减数变成整十数算起来更简单!减数 6 增添 4,总的小圆点(被减数)也就随着增添了 4(发现了没)。
减数增添多少,被减数也增添多少,差不变。
减数减少多少,被减数也减少多少,差不变。
三、谁能讲讲为何要巧算19+25=的计算方法:1、2、 19+2519+1-1+25=20+241= 4444四、计算 20 道两位数加两位数,分别用竖式和巧算,看看哪一种方法快!1、 28+17=2、55+27=3、 36+45=4、28+14=5、 36+37=6、39+15=7、 14+27=8、28+13=9、 19+22=10、26+38= 11、27+16=12、54+29= 13、28+16=14、37+28= 15、45+56=16、29+13= 17、28+14=18、35+27= 19、12+39=20、56+27=。