掌握线面角的定义(精)

浅谈线线角、线面角、面面角的定义方式北京市顺义区第九中学101300高中阶段在学习空间线、面位置关系的时候，会给出线线角、线面角及面面角的定义，本文以角形成的定义方式及蕴含的基本思想为主，进行研究。

1、直线与直线所成的角：（1）共面：同一平面内的两直线所成角，是利用两直线位置关系，平行、重合所成角为0度，如果相交就取交线所构成的锐角（或直角）。

（2）异面：如图所示，已知两条异面直线a和b,经过空间任一点O分别作直线a′∥a，b′∥b，我们把直线a′与b′所成的角叫做异面直线a与b所成的角（或夹角）。

θ定义方式：是发生定义法（即构造定义方式）定义中的“空间中任取一点O”，意味着：角的大小与O 点选取的位置无关；通过平移把异面直线所成角转化成两相交直线，是将空间图形问题转化成平面图形问题的定义方式，体现了定义的纯粹性和完备性。

2、直线和平面所成的角：如图，一条直线和一个平面相交，但不与这个平面垂直，这条直线叫做这个平面的斜线，斜线和平面的交点A叫做斜足.过斜线上斜足以外的一点P向平面引垂线PO，过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角，叫做这条直线和这个平面所成的角。

规定：一条直线垂直于平面，我们说它们所成的角是直角；一条直线和平面平行，或在平面内，我们说它们所成的角是0°的角。

3、面面所成的角：(1)在二面角的棱l上任取一点O，以该点O为垂足，在半平面和内分别作垂直于棱l的射线OA和OB，则射线OA和OB构成的角称为二面角的平面角.( 2)作二面角的平面角的方法方法一：(定义法)在二面角的棱上找一个特殊点，在两个半平面内分别作垂直于棱的射线．如图所示，∠AOB为二面角α­a­β的平面角．方法二：(垂线法)过二面角的一个面内一点作另一个平面的垂线，过垂足作棱的垂线，连接该点与垂足，利用线面垂直可找到二面角的平面角或其补角．如图所示，∠ACB为二面角α­m­β的平面角．4、线线、线面、面面所成角的定义方式线线、线面、面面所成角的定义方式是“属加种差定义法”。

高中数学线面角教案
教学目标：
1. 理解线面角的概念及其特点。

2. 掌握线面角的基本性质。

3. 能运用线面角的知识解决相关问题。

教学内容：
1. 线面角的定义。

2. 线面角的种类。

3. 线面角的性质及相关定理。

教学步骤：
一、导入（5分钟）
教师引入线面角的概念，以实际生活中的角度为例，让学生对线面角有一个直观的认识。

二、讲解（15分钟）
1.讲解线面角的定义及性质。

2.讲解线面角的种类，如平面角、平行线面角等。

三、练习（20分钟）
1.提供一系列练习题，让学生巩固线面角的概念和相关性质。

2.指导学生完成相关练习题，并讲解解题思路。

四、拓展（10分钟）
引导学生拓展思维，探讨线面角在其他几何问题中的应用，如平行线、相似三角形等。

五、总结（5分钟）
要求学生总结本节课所学的知识点，并提出问题和疑惑。

六、作业布置（5分钟）
布置相关作业，巩固学生所学知识，并要求学生在课后复习相关内容。

教学资源：
1. 教材内容
2. 多媒体教学PPT
3. 练习题集
教学反思：
在教学过程中，应重点讲解线面角的概念及性质，并引导学生通过实际练习题来巩固所学知识。

同时，要引导学生拓展思维，将线面角的知识与其他几何知识进行联系，以提高学生的综合应用能力。

线面角和二面角的范围一、引言线面角和二面角是几何学中的重要概念，广泛应用于计算机图形学、化学、材料科学等领域。

本文将详细介绍线面角和二面角的定义、计算方法以及其范围。

二、线面角的定义和计算方法1. 定义线面角是指直线与平面之间的夹角，即直线在平面上的投影与该直线本身之间的夹角。

它通常用于描述两个分子之间的相对位置关系。

2. 计算方法设直线L与平面P相交于点A，过点A作平面P上的垂线AD，则所求得的夹角就是∠LAD。

其中，LAD构成了一个直角三角形，因此可以使用三角函数来计算该夹角。

三、线面角的范围由于直线和平面可以任意取向，因此线面角没有固定的范围。

但是，在实际应用中，通常将其限制在0到180度之间。

四、二面角的定义和计算方法1. 定义二面角是指两个平面之间的夹角，即一个多面体两个相邻侧面所张开的空间部分所对应的立体角。

它通常用于描述多边形网格模型中不同面的相对位置关系。

2. 计算方法设多面体的两个相邻侧面分别为ABC和ABD，则所求得的二面角就是∠CABD。

其中，CABD构成了一个四面体，因此可以使用四面体立体角公式来计算该夹角。

五、二面角的范围二面角的范围通常被限制在0到180度之间。

在实际应用中，如果两个相邻侧面共线，则其二面角为0度；如果两个相邻侧面互相垂直，则其二面角为90度；如果两个相邻侧面背向而行，则其二面角为180度。

六、总结本文介绍了线面角和二面角的定义、计算方法以及其范围。

线面角是直线与平面之间的夹角，没有固定的范围；而二面角是两个平面之间的夹角，通常被限制在0到180度之间。

这些概念在计算机图形学、化学、材料科学等领域中有着广泛应用。

线面角线线角面面角的取值范围1. 引言嘿，大家好！今天我们来聊聊一个看似高深，其实跟我们生活息息相关的话题——线面角、线线角、面面角的取值范围。

听起来有点复杂？别担心，咱们慢慢来，保证你听完之后心里有个明白的数。

这就像一碗热腾腾的汤，虽然材料多，但调和之后，味道才是最重要的。

2. 线面角的魅力2.1 什么是线面角？首先，咱们得搞清楚线面角的定义。

简单来说，线面角就是一条线与一个平面之间形成的角度。

想象一下，你在地上画了一条线，天花板是一个平面，线和天花板之间的夹角就叫线面角。

这玩意儿看似简单，但其实背后可是有门道的。

2.2 线面角的取值范围那么，这个线面角的取值范围又是个啥呢？其实，线面角的取值范围是从0度到90度之间的。

也就是说，线和面之间可以有很多种不同的角度，但最极端的情况是，线完全垂直于面，角度就是90度；而当线跟面平行的时候，角度就是0度。

听起来像是数数，但实际应用可广泛得多，像建筑设计、机械制造等领域，线面角的掌控可是一门重要的技术活。

3. 线线角的多样性3.1 线线角是什么？接下来，我们来聊聊线线角。

这个名字听上去有点拗口，但其实它就是两条线之间的夹角。

比如说，两根棒子交叉在一起，咱们就能测量出它们之间的角度。

就像朋友之间的关系，有时亲密无间，有时又像两条平行线，永远不会相交，哈哈！3.2 线线角的取值范围那么，线线角的取值范围又如何呢？其实，它是从0度到180度之间的。

也就是说，线线角可以是小于90度的锐角，也可以是大于90度的钝角，甚至可以是180度的平角。

想象一下，两个朋友争论得不可开交，最后选择了平局，谁也不让谁，真是太有意思了！4. 面面角的奥秘4.1 面面角的定义最后，我们来看看面面角。

它就是两个平面之间形成的角度。

就像两扇门打开的角度，它们之间的关系就可以用面面角来描述。

这玩意儿可大可小，关键看门是开得多大。

4.2 面面角的取值范围面面角的取值范围从0度到180度，跟线线角有点类似。

线线角和线面角[重点]：确定点、斜线在平面内的射影。

[知识要点]：一、线线角1、定义：设a、b是异面直线，过空间一点O引a′//a,b′//b,则a′、b′所成的锐角(或直角),叫做异面直线a、b所成的角.2、范围:(0,]3. 向量知识：对异面直线AB和CD(1)；(2) 向量和的夹角<,>(或者说其补角)等于异面直线AB和CD的夹角；(3)二、线面角1、定义：平面的一条斜线和它在这个平面内的射影所成的锐角，斜线和平面所成角的范围是(0,).2、直线在平面内或直线与平面平行，它们所成角是零角；直线垂直平面它们所成角为，3、范围: [0,]。

4、射影定理：斜线长定理：从平面外一点向这个平面所引的垂线段和斜线段中：（1）射影相等的两条斜线段相等，射影较长的斜线段也较长；（2）相等的斜线段的射影相等，较长的斜线段的射影也较长；（3）垂线段比任何一条斜线段都短。

5、最小角定理：平面的一条斜线与平面所成的角，是这条直线和平面内过斜足的直线所成的一切角中最小的角。

6、向量知识（法向量法）与平面的斜线共线的向量和这个平面的一个法向量的夹角<,>(或者说其补角)是这条斜线与该平面夹角的余角.[例题分析与解答]例1．如图所示，在棱长为a的正方体ABCD-A1B1C1D1中，求：异面直线BA1与AC所成的角.分析：利用，求出向量的夹角,再根据异面直线BA1，AC所成角的范围确定异面直线所成角.解：∵，，∴∵AB⊥BC，BB1⊥AB，BB1⊥BC，∴∴又∴∴所以异面直线BA1与AC所成的角为60°.点评：求异面直线所成角的关键是求异面直线上两向量的数量积，而要求两向量的数量积，必须会把所求向量用空间的一组基向量来表示.例2．如图(1)，ABCD是一直角梯形，AD⊥AB，AD//BC，AB=BC=a, AD=2a,且PA⊥平面ABCD，PD与平面ABCD成30°角.(1)若AE⊥PD，E为垂足，求证：BE⊥PD；(2)求异面直线AE与CD所成角的大小（用反三角函数表示）解法一：（1）证明：∵PA⊥平面ABCD，∴PA⊥AB，∵AD⊥AB，∴AB⊥平面PAD，∴AB⊥PD，又AE⊥PD，∴PD⊥平面ABE，∴BE⊥PD.(2)解：设G、H分别为ED、AD的中点，连BH、HG、GB（图（1））易知，∴BH//CD.∵G、H分别为ED、AD的中点，∴HG//AE则∠BHG或它的补角就是异面直线AE、CD所成的角，而，，，在ΔBHG中，由余弦定理，得，∴.∴异面直线AE、CD所成角的大小为.解法二：如图（2）所示建立空间直角坐标系A-xyz，则，，，，，（1）证明：∵∴∴∴（2）解：∵∴∴异面直线AE、CD所成角的大小为例3．如图，在正方体ABCD-A1B1C1D1中，，求BE1与DF1所成角的余弦值.解：以D为坐标原点，为x,y,z轴，建立空间直角坐标系D-xyz，设正方体的棱长为4，则D(0,0,0)，B(4,4,0),E1(4,3,4), F1(0,1,4).则，∴，∵.∴∴BE1与DF1所成角的余弦值为点评：在计算和证明立体几何问题中，若能在原图中建立适当的空间直角坐标系，把图形中的点的坐标求出来，那么图形有关问题可用向量表示.利用空间向量的坐标运算来求解，这样可以避开较为复杂的空间想象。

专题3-1几何法求二面角，线面角立体几何空间向量求解过程，丧失了立体几何求解的乐趣，无形中也降低了学生的空间想象能力。

这是空间向量求解的巨大优点，也是缺点，就这么共存着。

其实不建系而直接计算真的很比较锻炼空间想象的能力，方法上也更灵活一些，对于备考的中档学生来说，2种方法都要熟练掌握。

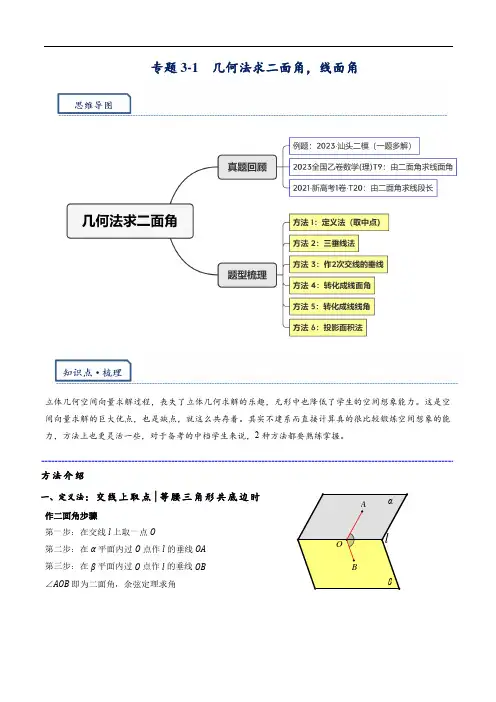
方法介绍一、定义法：交线上取点 等腰三角形共底边时作二面角步骤第一步：在交线l上取一点O第二步：在α平面内过O点作l的垂线OA第三步：在β平面内过O点作l的垂线OB∠AOB即为二面角，余弦定理求角αβl OAB二、三垂线法（先作面的垂直）—后续计算小使用情况：已知其中某个平面的垂线段第二步：过垂直B作l的垂线OB∠AOB即为二面角且△AOB为直角三角形，邻比斜三、作2次交线的垂线作二面角步骤第一步：作AO⊥l第二步：作OB⊥l连接AB，∠AOB即为二面角，余弦定理求角四、转换成线面角作二面角步骤第一步：作AO⊥l第二步：作AB⊥β(找不到垂足B的位置用等体积求AB长)连接AB，∠AOB即为二面角△AOB为直角三角形，邻比斜五、转换成线线角—计算小，也是法向量的原理提问：什么时候用？若α平面存在垂线AB，且β平面存在垂线AC则α平面与β平面的夹角等于直线AC与AB的夹角αβlOABαβlOABβαOABCαβlOAB六、投影面积法——面积比（三垂线法进阶）将cos θ＝边之比∣面积之比，从一维到二维，可多角度求出两面积，最后求解如图△ABC 在平面α上的投影为△A 1BC ， 则平面α与平面ABC 的夹角余弦值1cos A BCABCθ=△△即cos θ=投影原S S补充：即使交线没有画出来也可以直接用例题：一题多解2023汕头二模T20如图在正方体ABCD －A 1B 1C 1D 1中，PQ 是所在棱上的中点.1C 1CD ABA B 1αBCAA 1D（1）求平面APQ 与平面ABCD 夹角的余弦值 （2）补全截面APQ2023全国乙卷数学(理)T9——由二面角求线面角P C 1CDABA B 1P C 1DABA B 1P C 1CDABA B 1P C 1DABA B 1P C 1CDABA B 1PC 1DABA B 11．已知ABC 为等腰直角三角形，AB 为斜边，ABD △为等边三角形，若二面角C AB D −−为150︒，则直线CD 与平面ABC 所成角的正切值为（ ）A ．15B ．25C ．35D ．252021·新高考1卷·T20——由二面角求线段长2．如图，在三棱锥A BCD −中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D −−的大小为45︒，求三棱锥A BCD −的体积.题型一 定义法1．如图，在三棱锥S—ABC 中，SC ⊥平面ABC ，点P 、M 分别是SC 和SB 的中点，设PM=AC =1，∠ACB =90°，直线AM 与直线SC 所成的角为60°.(1)求证：平面MAP ⊥平面SAC . (2)求二面角M—AC—B 的平面角的正切值；2．(湛江期末)如图，在三棱锥P －ABC 中，PA ⊥平面ABC ，点M ，N 分别是PB ，AC 的中点，且MN ⊥A C ． （1）证明：BC ⊥平面PA C ．（2）若PA ＝4，AC ＝BC ＝22，求平面PBC 与平面AMC 夹角的余弦值．(几何法比较简单)3．如图1，在平行四边形ABCD 中，60,2,4A AD AB ∠=︒==，将ABD △沿BD 折起，使得点A 到达点P ，如图2．重点题型·归类精讲(1)证明：平面BCD⊥平面P AD；(2)当二面角D PA B−−的平面角的正切值为6时，求直线BD与平面PBC夹角的正弦值．题型二三垂线法4．(佛山期末)如图，四棱锥P－ABCD中，AB∥CD，∠BAD＝90°，12PA AD AB CD===，侧面PAD⊥底面ABCD，E为PC的中点．（1）求证：BE⊥平面PCD；（2）若PA＝PD，求二面角P－BC－D的余弦值．5．如图，在四棱锥P -ABCD 中，△P AD 是以AD 为斜边的等腰直角三角形，,,224,23BC AD CD AD AD CD BC PB ⊥====∥ （2023广州一模T19）（1） 求证：AD PB ⊥；（2）求平面P AB 与平面ABCD 交角的正弦值.6．如图，在三棱锥A BCD −中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点．（1）证明：OA CD ⊥；（2）若OCD 是边长为2的等边三角形，点E 在棱AD 上，2DE EA =且二面角E BC D −−的大小为60，求三棱锥A BCD −的体积．7．（2023·浙江·统考二模）如图，在三棱柱111ABCA B C 中，底面ABC ⊥平面11AA B B ，ABC 是正三角形，D 是棱BC 上一点，且3CD DB =，11A A A B =.(1)求证：111B C A D ⊥；(2)若2AB =且二面角11A BC B −−的余弦值为35，求点A 到侧面11BB C C 的距离.8．如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，ABC 和ACD 均为正三角形，4AC =，3BE =.(1)在线段AC 上是否存在点F ，使得BF ∥平面ADE ?说明理由； (2)求平面CDE 与平面ABC 所成的锐二面角的正切值.题型三 作2次交线的垂线9．在三棱锥S ABC −中,底面△ABC 为等腰直角三角形,90SAB SCB ABC ∠=∠=∠=︒. （杭州二模） （1）求证：AC ⊥SB ；（2）若AB ＝2，22SC =，求平面SAC 与平面SBC 夹角的余弦值．题型四 找交线10．如图，在四棱锥P －ABCD 中，底面ABCI )是平行四边形，∠ABC ＝120°，AB ＝1，BC ＝2，PD ⊥C D ． (1)证明：AB ⊥PB ；(2)若平面PAB ⊥平面PCD ，且102PA =，求直线AC 与平面PBC 所成角的正弦值． （广东省二模T19）题型五 转换成线线角湖北省武汉市江汉区2023届高三上学期7月新起点考试11．在直三棱柱111ABC A B C −中，已知侧面11ABB A 为正方形，2BA BC ==，D ，,E F 分别为AC ，BC ，CC 1的中点，BF ⊥B 1D ．(1)证明：平面B 1DE ⊥平面BCC 1B 1；(2)求平面BC 1D 与平面1B DE 夹角的余弦值六、 题型六 投影面积法12．(2022·惠州第一次调研)如图，在四棱锥P －ABCD 中，已知//AB CD ，AD ⊥CD ，BC BP =，CD ＝2AB＝4，△ADP 是等边三角形，E 为DP 的中点．(1)证明：AE ⊥平面PCD ；(2)若2,PA =求平面PBC 与平面PAD 夹角的余弦值13．(2022深圳高二期末)如图(1)，在直角梯形ABCD 中，AB //CD ，AB ⊥BC ，且12,2BC CD AB ===取AB 的中点O ，连结OD ，并将△AOD 沿着OD 翻折，翻折后23AC =M ，N 分别是线段AD ，AB 的中点，如图(2)．（1）求证：AC⊥OM.（2）求平面OMN与平面OBCD夹角的余弦值．专题3-1几何法求二面角，线面角立体几何空间向量求解过程，丧失了立体几何求解的乐趣，无形中也降低了学生的空间想象能力。

诚西郊市崇武区沿街学校高二数学〔下〕复习讲义〔1〕线面角与面面角一、知识与方法要点：1．斜线与平面所成的角就是斜线与它在平面内的射影的夹角。

求斜线与平面所成的角关键是找到斜线在平面内的射影，即确定过斜线上一点向平面所作垂线的垂足，这时经常要用面面垂直来确定垂足的位置。

假设垂足的位置难以确定，可考虑用其它方法求出斜线上一点到平面的间隔。

2．二面角的大小用它的平面角来度量，求二面角大小的关键是找到或者者作出它的平面角(要证明)。

作二面角的平面角经常要用三垂线定理，关键是过二面角的一个面内的一点向另一个面作垂线，并确定垂足的位置。

假设二面角的平面角难以作出，可考虑用射影面积公式求二面角的大小。

3．断定两个平面垂直，关键是在一个平面内找到一条垂直于另一个平面的直线。

两个平面垂直的性质定理是：假设两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．二、例题例1．正方体ABCD-A1B1C1D1中，M为C1D1中点．(1)求证：AC1⊥平面A1BD．(2)求BM与平面A1BD成的角的正切值．解：(1)连AC，∵C1C⊥平面ABCD，∴C1C⊥BD．又AC⊥BD，∴AC1⊥BD．同理AC1⊥A1B∵A1B∩BD=B．∴AC1⊥平面A1BD ．(2)设正方体的棱长为a ，连AD1，AD1交A1D 于E ，连结ME ，在△D1AC1中，ME∥AC1，∵AC1⊥平面A1BD ．∴ME⊥平面A1BD ．连结BE ，那么∠MBE 为BM 与平面A1BD 成的角．在Rt MEB ∆中，1322AC ME==， 22262BE a a ⎛⎫=+= ⎪ ⎪⎝⎭，∴2tan 2ME MBE BE ∠==．例2．如图，把等腰直角三角形ABC 以斜边AB 为轴旋转，使C 点挪动的间隔等于AC 时停顿，并记为点P ． 〔1〕求证：面ABP⊥面ABC ；〔2〕求二面角C-BP-A 的余弦值． 证明〔1〕 由题设知AP ＝CP ＝BP ．∴点P 在面ABC 的射影D 应是△ABC 的外心， 即D∈AB．∵PD⊥AB，PD ⊂面ABP ， 由面面垂直的断定定理知，面ABP⊥面ABC ． 〔2〕解法1 取PB 中点E ，连结CE 、DE 、CD ． ∵△BCP 为正三角形，∴CE⊥BD．△BOD 为等腰直角三角形，∴DE⊥PB．∴∠CED 为二面角C-BP-A 的平面角． 又由〔1〕知，面ABP⊥面ABC ，DC⊥AB，AB ＝面ABP∩面ABC ，由面面垂直性质定理，得DC⊥面ABP ．∴DC⊥DE．因此△CDE 为直角三角形．设1BC =，那么32CE =，12DE =，132cos 332DE CED CE ∠===． 例3．如下列图，在正三棱柱111ABC A B C -中，1E BB ∈，截面1A EC ⊥侧面1AC ．(1)求证：1BE EB =；(2)假设111AA A B =，求平面1A EC 与平面111A B C所成二面角(锐角)的度数．证明：在截面A1EC 内，过E 作EG⊥A 1C ，G 是垂足，如图，∵面A 1EC⊥面AC 1，∴EG⊥侧面AC 1．取AC 的中点F ，分别连结BF 和FC ，由AB ＝BC 得BF⊥AC． ∵面ABC⊥侧面AC 1，∴BF⊥侧面AC 1，得BF∥EG．BF 和EG 确定一个平面，交侧面AC 1于FG ． ∵BE∥侧面AC 1，∴BE∥FG，四边形BEGF 是，BE ＝FG ．∴BE∥AA 1，∴FG∥AA 1，△AA 1C∽△FGC． 解：(2)分别延长CE 和C1B1交于点D ，连结A 1D ． ∵∠B 1A 1C 1＝∠B 1C 1A 1＝60°，∴∠DA 1C 1＝∠DA 1B 1＋∠B 1A 1C 1＝90°，即DA 1⊥A 1C 1． ∵CC 1⊥面A 1C 1B 1，由三垂线定理得DA 1⊥A 1C ，所以∠CA 1C 1是所求二面角的平面角．且∠A 1C 1C ＝90°． ∵CC 1＝AA 1＝A 1B 1＝A 1C 1，∴∠CA 1C 1＝45°，即所求二面角为45°． 说明：假设改用面积射影定理，那么还有另外的解法．三、作业： 1．平面的一条斜线a 与平面成角，直线b，且a,b 异面，那么a 与b 所成的角为〔A 〕A ．有最小值，有最大值2π B ．无最小值，有最大值2π。

线线角,线面角,面面角的公式
线线角：
1、定义：线线角是由两条相交的直线上所标注的交汇夹角。

2、公式：计算线线角的公式是以弧度为单位的夹角的函数，公式为：
ϴ=arctan[(y2-y1)/(x2-x1)]。

3、特殊情况下：当两条直线平行时，线线角是否存在？此时两条直线不相交，因此没有线线角存在；当两条直线重合时，此时也可以设定一个夹角为0度的直角，这样线线角的值也是零。

线面角：
1、定义：线面角是指一条直线与一个平面相交时，定义的一个夹角。

2、公式：计算线面角的公式为θ=arccos[n∙l/|n||l|]，其中n是平面的法向量，l是直线上的位置向量。

3、特殊情况下：当线与平面垂直时，线面角的值为90度，即θ=π/2；当线与平面平行时，线面角的值为零，即θ=0。

面面角：
1、定义：面面角是两个平面在不同方向上接触的交点夹角。

2、公式：计算面面角的公式为θ=arccos[n1∙n2/|n1||n2|]，其中n1、n2是平面的法向量。

3、特殊情况下：当两平面垂直时，面面角的值为90度，即θ=π/2；当两平面平行时，面面角的值为零，即θ=0。

线面直线所成的角线面直线所成的角是指当一条直线与一个面相交时，所形成的两个角。

一个角位于面的一侧，被称为外角；另一个角位于面的另一侧，被称为内角。

线面直线所成的角在几何学中经常被应用，具有重要的实际意义和应用价值。

1.概述线面直线所成的角线面直线所成的角是指当一条直线与一个面相交时所形成的两个角。

这两个角是外角和内角。

外角是指直线位于面的一侧，被称为外的角度；内角则位于面的另一侧，被称为内角。

外角和内角的度数加起来等于180度。

2.线面直线所成角的性质和特点线面直线所成的角具有一些性质和特点，这些性质和特点可以用于解决与线面直线相关的问题。

(1)线面直线所成的角相等性如果两条直线与同一个面相交，且它们分别形成的角相等，则这两条直线就是相等的。

(2)线面直线所成的角互补性如果两条直线与同一个面相交，且一个角是直角，则这两条直线就是互相垂直的。

(3)线面直线所成的角的平行性如果两条直线与同一个平面相交，且它们分别形成的内角相等，则这两条直线是平行的。

(4)线面直线所成的角的补角性如果两条直线与同一个面相交，且一个角是直角，则这两个角是补角。

3.线面直线所成角的应用线面直线所成的角在几何学中有着广泛的应用。

它们可以帮助我们解决许多与线面直线相关的实际问题。

(1)斜面与地面的夹角当一个斜面与地面相交时，它们形成了一条直线与一个面相交的情况。

这时，斜面与地面的夹角就是线面直线所成的角。

我们可以利用斜面与地面的夹角来计算斜面的倾斜程度，以及在斜面上放置物体时的稳定性。

(2)航空航天中的进近角在航空航天领域中，进近角指的是飞机或火箭的飞行航向与水平面之间的夹角。

进近角可以影响飞行器的进近路径和着陆速度。

通过调整进近角，可以更好地控制飞行器的下滑角度和速度，以确保安全着陆。

(3)地理学中的地球与赤道的倾角地球的自转轴与赤道面之间的夹角被称为地球的倾角。

地球的倾角对地球的季节变化和气候分布有着重要的影响。

通过研究地球的倾角，我们可以更好地理解地球的旋转规律，以及不同地区季节变化的原因。

线线角和线面角[重点]：确定点、斜线在平面内的射影。

[知识要点]：一、线线角1、定义：设a、b是异面直线，过空间一点O引a′//a,b′//b,则a′、b′所成的锐角(或直角),叫做异面直线a、b所成的角.2、范围:(0,]3. 向量知识：对异面直线AB和CD(1)；(2) 向量和的夹角<,>(或者说其补角)等于异面直线AB和CD的夹角；(3)二、线面角1、定义：平面的一条斜线和它在这个平面内的射影所成的锐角，斜线和平面所成角的范围是(0,).2、直线在平面内或直线与平面平行，它们所成角是零角；直线垂直平面它们所成角为，3、范围: [0,]。

4、射影定理：斜线长定理：从平面外一点向这个平面所引的垂线段和斜线段中：（1）射影相等的两条斜线段相等，射影较长的斜线段也较长；（2）相等的斜线段的射影相等，较长的斜线段的射影也较长；（3）垂线段比任何一条斜线段都短。

5、最小角定理：平面的一条斜线与平面所成的角，是这条直线和平面内过斜足的直线所成的一切角中最小的角。

6、向量知识（法向量法）与平面的斜线共线的向量和这个平面的一个法向量的夹角<,>(或者说其补角)是这条斜线与该平面夹角的余角.[例题分析与解答]例1．如图所示，在棱长为a的正方体ABCD-A1B1C1D1中，求：异面直线BA1与AC所成的角.分析：利用，求出向量的夹角,再根据异面直线BA1，AC所成角的范围确定异面直线所成角.解：∵，，∴∵AB⊥BC，BB1⊥AB，BB1⊥BC，∴∴又∴∴所以异面直线BA1与AC所成的角为60°.点评：求异面直线所成角的关键是求异面直线上两向量的数量积，而要求两向量的数量积，必须会把所求向量用空间的一组基向量来表示.例2．如图(1)，ABCD是一直角梯形，AD⊥AB，AD//BC，AB=BC=a, AD=2a,且PA⊥平面ABCD，PD与平面ABCD成30°角.(1)若AE⊥PD，E为垂足，求证：BE⊥PD；(2)求异面直线AE与CD所成角的大小（用反三角函数表示）解法一：（1）证明：∵PA⊥平面ABCD，∴PA⊥AB，∵AD⊥AB，∴AB⊥平面PAD，∴AB⊥PD，又AE⊥PD，∴PD⊥平面ABE，∴BE⊥PD.(2)解：设G、H分别为ED、AD的中点，连BH、HG、GB（图（1））易知，∴BH//CD.∵G、H分别为ED、AD的中点，∴HG//AE则∠BHG或它的补角就是异面直线AE、CD所成的角，而，，，在ΔBHG中，由余弦定理，得，∴.∴异面直线AE、CD所成角的大小为.解法二：如图（2）所示建立空间直角坐标系A-xyz，则，，，，，（1）证明：∵∴∴∴（2）解：∵∴∴异面直线AE、CD所成角的大小为例3．如图，在正方体ABCD-A1B1C1D1中，，求BE1与DF1所成角的余弦值.解：以D为坐标原点，为x,y,z轴，建立空间直角坐标系D-xyz，设正方体的棱长为4，则D(0,0,0)，B(4,4,0),E1(4,3,4), F1(0,1,4).则，∴，∵.∴∴BE1与DF1所成角的余弦值为点评：在计算和证明立体几何问题中，若能在原图中建立适当的空间直角坐标系，把图形中的点的坐标求出来，那么图形有关问题可用向量表示.利用空间向量的坐标运算来求解，这样可以避开较为复杂的空间想象。

线面角二面角线线角的公式线面角、二面角和线线角是在几何学中常见的概念，它们有各自的计算公式。

下面将分别介绍这三个角的定义和计算方法。

1.线面角：线面角是由一条线与一个平面相交所形成的角。

设平面上有一条直线L，平面上有一点A和直线上的一点B，在平面上从点A引一条垂线，与直线L相交，就形成了一个线面角。

线面角的度量是直线L的角度与平面的夹角。

线面角的计算公式如下：线面角=直线L与平面的夹角2.二面角：二面角是由两个平面相交所形成的角。

设有一个平面P1和一个不与P1平行的平面P2，两个平面相交于一条直线L。

通过P1和P2的交线L 可以确定两个交点A和B。

二面角的计算公式如下：二面角=（直线L在P1中所成的角）+（直线L在P2中所成的角）值得注意的是，二面角没有固定的度量单位，它的度量取决于直线L 在两个平面上的角度度量单位。

3.线线角：线线角是由两条直线相交所形成的角。

设有两条直线L1和L2，它们相交于一点O。

通过O可以确定L1上的一点A和L2上的一点B。

线线角的计算公式如下：线线角=∠AOB其中，∠AOB表示点A、O和B所形成的角。

总结：线面角、二面角和线线角是几何学中常见的角度概念。

线面角由一条直线与一个平面相交所形成，计算公式为线面角=直线L与平面的夹角。

二面角由两个平面相交所形成，计算公式为二面角=（直线L在P1中所成的角）+（直线L在P2中所成的角）。

线线角由两条直线相交所形成，计算公式为线线角=∠AOB。

这些角度概念在几何学的应用中起着重要的作用。

直线和平面所成的角、二面角都是教学大纲和高考考纲要求掌握的，是立体几何的重点内容，也是高考的必考内容.要熟练掌握它们，需要从以下四个方面入手。

一、1个公式公式12cos cos cos q q q =中涉及三个角，q 是指平面的斜线l 与平面内过斜足且不同于射影的直线m 所在所成的角，1q 是指l 与其射影'l 所成的角，2q 是指'l 与m 所成的角.其中210cos 1,.q q q <<<由此可得最小角定理.二、2个定义1.线面角：一个平面的斜线和它在这个平面内的射影所成的角，叫做斜线和这个平面所成的角（斜线和平面的夹角）.如果直线和平面垂直，那么就说直线和平面所成的角是直角；如果直线和平面平行或直线在平面内，那么说直线和平面所成的角是零度的角.直线和平面所成的角的取值范围为[0,90]鞍，斜线和平面所成角的取值范围为(0,90)鞍.2.二面角：从一条直线出发的两个半平面所组成的图形叫做二面角，其中直线、半平面分别叫做二面角的棱和面.一个平面垂直于二面角l a b --的棱l ，且与两个半平面的交线分别是射线OA OB 、，O 为垂足，则AOB Ð叫做二面角l a b --的平面角.它决定着二面角的大小.其中平面角是直角的二面角叫做直二面有，相交成直二面角的两个平面叫做互相垂直的平面.二面角的取值范围为[0,180]鞍.三、3个定理1.最小角定理：平面的斜线和它在平面内的射影所成的角，是这条斜线和这个平面内任一条直线所成的角中最小的角.2.平面与平面垂直的判定定理：如果一个平面过另一个平面的一条垂线，那么这两个平面互相垂直.3.平面与平面垂直的性质定理：如果两个平面互相垂直，那么在一个平面内垂直它们交线的直线垂直于另一个平面.四、4类求法1.几何法求直线和平面的夹角：根据直线和平面所成角的定义，先找出或作出直线在平面内的射影，然后把直线、射影对应的线段放在三角形中进行求解，其中能够寻找到垂直关系用直角三角形求解更佳.2.向量法求直线和平面的夹角：主要适用于图形比较规则，容易建立空间直角坐标系或容易选择空间向量的基底(要求作为基底的三个向量的模及夹角已知)的题目.(1)平面向量法：在斜线上取向量a 和其射影上取向量'a (注意方向，夹角为锐角)，则|'|c o s ,'|||'|a a a a a a ×<>=×，这里a 、'a 形式上在同一个平面内；(2)法向量法：在斜线上取向量a ，并求出平面的法向量n ，所求夹角记为q ，则||sin |cos ,|||||a n a n a n q ×=<>=×，所以||arcsin ||||a n a n q ×=×.需要注意的是，当法向量与坐标平面平行或垂直时，可以直接给出法向量，当法向量与坐标平面不平行也不垂直时，由于法向量不唯一，不妨设横坐标、纵坐标、竖坐标中的某一个坐标为1，而且尽量让1以外的坐标在点乘中与0相乘，这样计算量较小.3.几何法求二面角的大小：(1)定义法(垂面法)：过二面角内的一点作棱的垂面，垂面与二个半平面的交线形成所求平面角. (2)等价定义法：在二面角的棱上取一点(中点等特殊点) ，分别在两个半平面内作棱的垂线，得出平面角.(3)三垂线法：先作(或找)出二面角的一个面内一点到另一个面的垂线，用三垂线定理或逆定理作出平面角.(4)射影面积法：利用面积射影公式cos S S q =射投其中 为平面角的大小，特点在于不需要画出平面角，也不需要找出棱，尤其适用于没有画出棱的二面角问题.4.向量法求二面角的大小：图形比较规则，又不容易直接作出平面角的具体顶点时，可采用此法.(1)平面向量法:在棱上取一平面角的顶点，利用向量垂直时点乘等于零，求出平面角顶点的坐标，进而转化为向量夹角问题，此时两个向量形式上在同一个平面内.(2)空间向量法：方法基本同(1)，此时两个向量形式上不在同一个平面内，思维量、运算都小一些，试题更具有一般性.(3)法向量法：建立空间直角坐标系后，分别求出两个平面的法向量,，利用公式||||,cos n m ⋅>=<.另外：证明两个平面垂直的关键是面面垂直转化为线面垂直；两个平面垂直的性质应用关键是在一个平面内找出两个平面交线的垂线.利用向量知识求线线角，线面角，二面角的大小。

线面角的计算公式线面角在数学和几何中是一个非常重要的概念。

它与平面和空间图形的研究有着密切的关系，同时也在日常生活中具有很大的应用。

在本文中，我们将介绍线面角的定义、计算公式以及如何应用这些公式。

1. 线面角的定义首先，我们需要了解什么是线面角。

线面角是由一条线段与一个平面形成的夹角。

当我们将线段平移到平面上时，它将会成为一个角，这个角就是线面角。

线面角有两个端点，一个位于线段所在的点，另一个位于线段与平面相切的点。

线面角是一种度量角度大小的方法。

通常用弧度或度数来表示。

弧度是一个圆心角所对的角度，它的单位是弧长与半径的比值。

度数是每个角度有360个度的计量方法。

2. 线面角的计算公式线面角的计算公式可以根据情况有所不同。

下面列出一些常用的公式以供参考。

（1）线面角的弧度表示如果用弧度表示线面角，则公式为：线面角（弧度）= 弧长 / 半径例如，一条长4米的线段与一个半径为2米的球体相交。

则线面角的弧度表示为：线面角（弧度）= 4 / 2 = 2（2）线面角的度数表示如果用度数表示线面角，则公式为：线面角（度数）= 弧度/ π × 180°例如，如果线面角的弧度表示为2，则线面角的度数表示为：线面角（度数）= 2 / π × 180° ≈ 114.59°（3）线面角的余弦值线面角的余弦值可以用来计算两个线面角之间的夹角。

公式如下：cos θ = a · b / |a| × |b|其中，a 和 b 分别代表两个向量，|a| 和 |b| 分别代表它们的模长。

θ 代表两向量之间的夹角。

例如，如果有两条线段 a 和 b，它们的向量分别为a = (1,2,3)b = (4,5,6)则它们之间的线面角的余弦值为：cos θ = (1 · 4 + 2 · 5 + 3 · 6) / √(1² + 2² + 3²) × √(4² + 5² + 6²) ≈ 0.974（4）线面角的正弦值线面角的正弦值可以用来计算线面角所在平面与另一平面之间的夹角。

线面角面面角线线角的取值范围一、前言线面角面面角线线角是几何学中常见的概念，对于初学者来说，理解这些概念的取值范围是非常重要的。

本文将详细介绍线面角面面角线线角的定义及其取值范围。

二、线1. 定义在几何学中，一条直线是由无数个点组成的无限长的集合。

直线可以用两个端点来确定。

2. 取值范围直线没有长度和宽度，因此其取值范围为无穷大。

三、面1. 定义在几何学中，一个平面是由无数个点组成的二维图形。

平面可以用三个点或一条直线和一个点来确定。

2. 取值范围平面没有体积和厚度，因此其取值范围为无穷大。

四、角1. 定义在几何学中，一个角是由两条相交的线段所组成的图形。

相交的两条线段称为角的边，它们相交的点称为角的顶点。

2. 取值范围一个角可以被分为四个部分：零度到90度之间称为锐角；90度称为直角；大于90度小于180度之间称为钝角；等于180度称为平角。

五、面角1. 定义在几何学中，一个面角是由三条相交的线段所组成的图形。

相交的三条线段称为面角的边，它们相交的点称为面角的顶点。

2. 取值范围一个面角可以被分为四个部分：小于90度称为锐面角；等于90度称为直面角；大于90度小于180度之间称为钝面角；等于180度称为平面角。

六、面角线1. 定义在几何学中，一个面角线是从一个顶点开始，穿过这个顶点所在的平面，并与另一条边相交而得到的一条线段。

2. 取值范围对于任意一个平面上的顶点来说，它可以连接该顶点和该平面上任意一点，因此其取值范围为无穷大。

七、线角1. 定义在几何学中，一个线角是由两条相交的直线所组成的图形。

相交的两条直线称为线角的边，它们相交的点称为线角的顶点。

2. 取值范围一个线角可以被分为四个部分：小于90度称为锐线角；等于90度称为直线角；大于90度小于180度之间称为钝线角；等于180度称为平线角。

八、总结通过以上的介绍，我们可以得出以下结论：- 线的取值范围为无穷大；- 面的取值范围为无穷大；- 角的取值范围为0到180度；- 面角的取值范围为0到180度；- 面角线的取值范围为无穷大；- 线角的取值范围为0到180度。

直线与法向量的夹角与线面角之间的关系1. 引言1.1 概述本文研究的主题是直线与法向量之间的夹角和线面角的关系。

在几何学中，直线和法向量是常见的概念，在各种应用领域中都有广泛的运用。

夹角作为两个向量之间的关系度量方式，对于理解直线和法向量之间的关联至关重要。

而线面角则描述了一条直线与一个平面之间的夹角，它与法向量也有着密切的联系。

通过探究这些数学概念之间的关系，我们可以更好地理解它们在几何学和实际应用中的意义及作用。

1.2 研究背景直线和法向量是几何学中基础而重要的概念，在计算机图形学、力学、物理等领域都有广泛应用。

在计算机图形学中，直线和法向量常被用来描述三维空间中物体的位置、方向和表面属性。

在力学和物理学中，直线代表了力或位移方向，而法向量指示了所研究对象所处位置或表面性质。

然而，在许多实际问题中，人们通常需要考虑到夹角和线面角这两个概念。

在解决问题中，正确理解和应用这些关系可以帮助我们更准确地分析和计算结果。

1.3 目的本文的目的是研究直线与法向量之间的夹角，并探讨夹角与线面角之间的关系。

通过数学推导和实例分析，我们将阐述直线与法向量夹角的定义、计算方法以及它们在实际问题中的应用。

同时，我们还将探讨线面角的定义、特性以及它与法向量之间的联系。

最后，本文将总结结论并展望未来可能的研究方向，为读者提供思考和启示。

通过本文对直线与法向量夹角和线面角之间关系的深入讨论，读者可以更全面地理解这些重要概念，在解决实际问题时能够灵活运用，并为进一步研究提供有益参考。

2. 直线与法向量的夹角：2.1 直线的定义及性质：直线是平面几何中的基本概念，它由无限多个点组成，并且在平面上没有宽度和厚度。

直线可以用一种简单而明确的方式表示，即通过两个不同的点。

两个不同点确定了唯一的一条直线。

在数学中，直线有着许多重要性质。

首先，任意两点都可以确定一条直线。

其次，直线上的任意两个点与第三个不在这条直线上的点构成一个三角形，而这个三角形将呈现出一些特殊性质。