线面角的求法

线面角的求法1．直接法 ：平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。

通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。

例1 （ 如图1 ）四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。

（2）SC 与平面ABC 所成的角。

BMHSCA解:（1） ∵SC ⊥SB,SC ⊥SA,图1∴SC ⊥平面SAB 故 SB 是斜线BC 在平面SAB 上的射影， ∴∠SBC 是直线BC 与平面SAB 所成的角为60°。

（2） 连结SM,CM ，则SM ⊥AB,又∵SC ⊥AB,∴AB ⊥平面SCM, ∴面ABC ⊥面SCM过S 作SH ⊥CM 于H, 则SH ⊥平面ABC ∴CH 即为 SC 在面ABC 内的射影。

∠SCH 为SC 与平面ABC 所成的角。

sin ∠SCH=SH ／SC∴SC 与平面ABC 所成的角的正弦值为√7／7（“垂线”是相对的，SC 是面 SAB 的垂线，又是面 ABC 的斜线. 作面的垂线常根据面面垂直的性质定理，其思路是：先找出与已知平面垂直的平面，然后一面内找出或作出交线的垂线，则得面的垂线。

） 2. 利用公式sin θ=h ／ι其中θ是斜线与平面所成的角， h 是 垂线段的长，ι是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可用三棱锥的体积自等来求垂线段的长。

例2 （ 如图2） 长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ，求AB 与面 AB 1C 1D 所成的角。

A 1C 1D 1H4C123BAD解：设点 B 到AB 1C 1D 的距离为h ，∵V B ﹣AB 1C 1=V A ﹣BB 1C 1∴1／3 S △AB 1C 1·h= 1／3 S △BB 1C 1·AB，易得h=12／5 ，设AB 与 面 A B 1C 1D 所成的角为θ,则sin θ=h ／AB=4／5，∴AB 与面AB 1C 1D 所成的角为arcsin0.83. 利用公式cos θ=cos θ1·cosθ2（如图3） 若 OA 为平面的一条斜线，O 为斜足，OB 为OA 在面α内的射影，OC 为面α内的一条直线，其中θ为OA 与OC 所成的角，B αOAC图3θ1为OA 与OB 所成的角，即线面角，θ2为OB 与OC 所成的角，那么 cos θ=cos θ1·cosθ2，它揭示了斜线和平面所成的角是这条斜线和这个平面内的直线所成的一切角中最小的角（常称为最小角定理）1．平面的斜线和平面所成的角：已知，如图，AO 是平面α的斜线，A 是斜足，OB 垂直于平面α，B 为垂足，则直线AB 是斜线在平面α内的射影。

求线面角的三种常见思路方法线面角是指直线与平面之间所形成的角，是几何学中一个重要的概念。

解线面角问题可以采用以下三种常见的思路方法：思路一：利用平行线的性质在解线面角问题时，常常会涉及到平行线的性质。

根据平行线的特征，可以使用以下思路来解决线面角问题：1.利用平行线的对应角相等和内错角相等性质。

如果已知两条直线平行，可以利用对应角相等和内错角相等的性质来求解线面角。

通过对已知条件进行分析，找到与线面角有关的对应角或内错角，利用性质得到所求的线面角的大小。

2.利用平行线与截线的交角性质。

当一条直线与两条平行线相交时，可以利用平行线与截线的交角性质来求解线面角。

根据已知条件，找到已知直线与平行线之间的交角，利用交角的性质计算出线面角的大小。

思路二：利用投影思想在解线面角问题时，可以利用投影的概念，将线面角问题转化为由线段形成的平面角的问题。

通过以下思路来解决线面角问题：1.利用垂直平分线的性质。

如果已知一条线段与平面之间的夹角，并且该线段的中垂线与平面垂直相交，就可以利用垂直平分线的性质求解线面角。

通过画出线段的垂直平分线，找到与线面角有关的平面角，根据平面角的性质计算出线面角的大小。

2.利用投影线段的长度比例。

当已知一条线段与平面之间的夹角，并且该线段在平面上的投影与线段本身的长度之间存在一定的比例关系时，可以利用投影线段的长度比例求解线面角。

通过给出的长度比例关系，利用投影线段的性质计算出线面角的大小。

思路三：利用旋转思想在解线面角问题时，可以借助旋转的概念，将线段或线面角问题转化为更容易解决的问题。

以下是利用旋转思想解决线面角问题的方法：1.利用其中一直线的旋转。

如果已知一条直线与平面之间的夹角，并且可以将该直线绕一个点旋转，使旋转后的直线与平面重合或相切，就可以利用旋转后的性质来求解线面角。

通过旋转后的直线与平面的位置关系，找到与线面角有关的平面角，根据平面角的性质求解线面角的大小。

2.利用绕轴旋转。

线面角的求法复习目标：1.理解直线与平面所成角的概念，并掌握求线面角常用方法．2.掌握求角的计算题步骤是“一作、二证、三计算”,思想方法是将空间图形转化为平面图形的思想方法.高考热点： 直线与平面所成角的求法知识整合:1.线面角(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫这条斜线和这个平面所成的角(2)若直线l ⊥平面α，则 l 与α所成角为直角若直线l ∥平面α，或直线l ⊂平面α，则l 与α所成角为0°(3)范围;⎥⎦⎤⎢⎣⎡2,0π方法一：直接法（几何法）.,,,,1111就是所求的线面角面于作，连接交于点连接G DD ACD DG G O D DG O D O CD AB ∠∴⊥⊥【解题回顾】“线面角定射影”也就是说要求直线与平面所成的角，关键是找到直线在此平面上的射影，为此，必须在这条直线上的某一点处作一条(或找一条)平面的垂线，本题中GD 就是平面的垂线.化归为平面几何问题来解决.方法二：活用线面角定义求解111133ACD ACD S DO S DD ∆∆⋅=⋅11D ACD D ACDV V --=n e n e n e l n e l ⋅==θϕθϕααcos sin ,,.2，则夹角为的，两向量所成角为与平面，直线的法向量为平面的方向向量为如图，设直线量求法直线和平面所成角的向.,111111所成角的余弦值与平面求直线中如图所示，正方体ACD BB D C B A ABCD -A B C D A1 B1C1 D1 O G .,//111111所成角相等与平面所成的角与与平面ACD DD ACD BB DD BB ∴ 由等体积法平面设,1ACD DG ⊥【解题回顾】先利用等体积法求出直线上某点到平面的距离，再由斜足、垂足、所取三点构成直角三角形求解.方法三：向量法【解题回顾】求线面角，常规解法“一作二证三求”，难在不易找到所求角，利用向量解法可避免“作、证”，只需利用公式，通过简单的向量计算即可解决，显现了向量这一工具巨大的作用. 变式训练：感悟 提高线面角的求解方法，一种是几何法，另 一种是向量法.1.几何法作角是关键，而确定斜线在平面内的射影是作角的突破口.2.向量法是把求角的问题转化为求两个向量的夹角，这里的平面法向量常用待定系数法求解，求平面法向量是关键.课后作业：a a a S DD S DO ACD ACD 3332311==⋅=∆∆36cos 33sin 111=∠∴==∠O DD DD DO O DD ())1,0,0(,1,1,1111==BB n ACD 又的法向量，易得平面设正方体棱长为解：如图建立坐标系，36cos 33131cos sin =∴=⋅=<=θθθn ，设所求角为_____.1111111成角的正弦值等于所与侧面等，则的侧棱长与底面边长相已知正三棱柱A ACC AB C B A ABC -.2190.21110111所成角的正弦值与面，求，，是等腰直角三角形，中，底面直三棱柱BC A BC AA AC ACB ABC C B A ABC ===∠-..,.31111111所成角的正弦值与平面求直线的中点是棱中，如图所示，正方体A ABB BE DD E D C B A ABCD -。

线线角-线面角的向量求法--
在几何中，线段与面的角度是指两个线段在空间上的夹角，一条线段穿过一个平面，产生了一个线面角。

它的计算是利用空间线段的垂直向量来求解的，它与传统的线线角的求法有所不同。

线面角的求法主要有以下三种：
（1）直接求解线段的垂直向量。

利用空间线段的垂直向量，可以比较容易地求出线面角，其具体步骤是：（1）确定两个空间线段，并计算出每条线段的斜率；（2）由斜率计算出线段的垂直向量；（3）通过两个垂直向量的夹角来求出线面角的余弦值，然后将余弦值转化为角度值，即，线面角的值。

（2）转换为线线角的求法。

首先，由空间线段可以构造出一个平面；然后，可以将两个空间线段在这个平面上展开，其中一条线段是斜45°展开，另一条线段则与它垂直，这样，就可以计算出展开后的两条线段间的夹角，这个夹角就是原来空间中的线面角。

（3）空间坐标描述求解法。

空间线段可以根据它的端点坐标来描述，给定每条线段的端点坐标，可以用端点坐标计算出空间线段的方向向量，由此可以计算出这两条线段的夹角，即空间中的线面角。

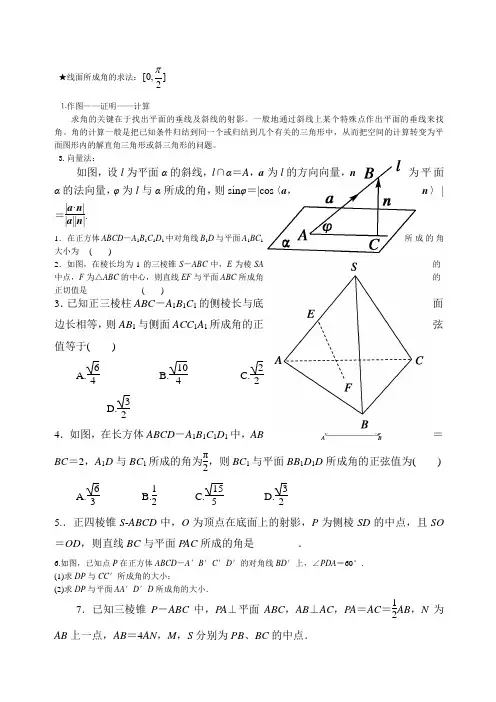
★线面所成角的求法：]2,0[⒈作图——证明——计算 求角的关键在于找出平面的垂线及斜线的射影。

一般地通过斜线上某个特殊点作出平面的垂线来找角。

角的计算一般是把已知条件归结到同一个或归结到几个有关的三角形中，从而把空间的计算转变为平面图形内的解直角三角形或斜三角形的问题。

3.向量法：如图，设l 为平面α的斜线，l ∩α＝A ，a 为l 的方向向量，n为平面α的法向量，φ为l 与α所成的角，则sin φ＝|cos 〈a ，n 〉|＝|a ·n ||a ||n |. 1．在正方体ABCD －A 1B 1C 1D 1中对角线B 1D 与平面A 1BC 1所成的角大小为 ( )2．如图，在棱长均为1的三棱锥S －ABC 中，E 为棱SA的中点，F 为△ABC 的中心，则直线EF 与平面ABC 所成角的正切值是 ( ) 3．已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则AB 1与侧面ACC 1A 1所成角的正弦值等于( ) A.64 B.104 C.22 D.32 4．如图，在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝2，A 1D 与BC 1所成的角为π2，则BC 1与平面BB 1D 1D 所成角的正弦值为( ) A.63 B.12 C.155 D.325.．正四棱锥S -ABCD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，则直线BC 与平面P AC 所成的角是________．6.如图，已知点P 在正方体ABCD －A ′B ′C ′D ′的对角线BD ′上，∠PDA ＝60°.(1)求DP 与CC ′所成角的大小；(2)求DP 与平面AA ′D ′D 所成角的大小．7．已知三棱锥P －ABC 中，P A ⊥平面ABC ，AB ⊥AC ，P A ＝AC ＝12AB ，N 为AB 上一点，AB ＝4AN ，M ，S 分别为PB 、BC 的中点．(1)证明：CM⊥SN；(2)求SN与平面CMN所成角的大小．8．如图，在五棱锥P-ABCDE中，P A⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，∠ABC＝45°，AB＝22，BC＝2AE＝4，三角形P AB是等腰三角形．(1)求证：平面PCD⊥平面P AC；(2)求直线PB与平面PCD所成角的大小；(3)求四棱锥P-ACDE的体积．9.如图所示，在正方体ABCD—A1B1C1D1中，E是棱DD1的中点．(1)求直线BE和平面ABB1A1所成的角的正弦值；(2)在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．10.如图，四棱锥PABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD＝PD，E，F分别为CD，PB的中点．(1)求证：EF⊥平面PAB；(2)设AB＝2BC，求AC与平面AEF所成角的正弦值．11．如图，四棱锥P-ABCD中，底面ABCD是矩形，P A⊥底面ABCD，P A＝AB＝1，AD＝3，点F是PB的中点，点E在边BC上移动．(1)点E为BC的中点时，试判断EF与平面PAC的位置关系. 并说明理由；(2)证明：无论点E在BC边的何处，都有PE⊥AF；(3)当BE等于何值时，PA与平面PDE所成角的大小为45°？。

线面角的求法总结三种求解线面角的方法1.直接法：当平面的斜线与斜线在平面内的射影相交时，它们所成的角即为直线与平面所成的角。

一般通过解直角三角形来计算，其中垂线段是最重要的元素，它可以联系各线段。

例如，在四面体ABCS中，SA、SB、SC两两垂直，且∠SBA=45°，∠SBC=60°，M为AB的中点，求（1）BC与平面SAB所成的角。

（2）SC与平面ABC所成的角。

解：（1）由于SC垂直于SB和SA，因此SB是BC在平面SAB上的射影，∴∠XXX为60°。

2）连接SM和CM，得到SM垂直于AB。

由于SC垂直于AB，因此AB垂直于平面SCM，从而面ABC垂直于面SCM。

过S作SH⊥CM于H，则SH⊥平面ABC，∴CH即为SC在面ABC内的射影。

因此，∠SCH为SC与平面ABC所成的角，其正弦值为√7／7.2.利用公式sinθ=h／ι，其中θ是斜线与平面所成的角，h是垂线段的长，ι是斜线段的长。

求出垂线段的长是关键也是难点，可以使用三棱锥的体积相等来求解。

例如，在长方体ABCD-A1B1C1D1中，AB=3，BC=2，A1A=4，求AB与面AB1C1D1所成的角的正弦值。

解：设点B到AB1C1D1的距离为h，由于VAB1C1D1=VA1B1C1D，因此1／3S△AB1C1·h=1／3S△BB1C1·AB，解得h=12／5.设AB与面AB1C1D1所成的角为θ，则sinθ=h／AB=4／5.3.利用公式cosθ=cosθ1·cosθ2已知，其中AO是平面α的斜线，A是斜足，OB垂直于平面α，B为垂足，则直线AB是斜线在平面α内的射影。

设AC是平面α内的任意一条直线，且OBC垂直于AC，垂足为C，则∠BAO=θ1，∠BAC=θ2.例如，如图所示，求直线AB与平面α所成的角的余弦值。

解：由于OB垂直于平面α，因此∠XXX即为直线AB与平面α所成的角。

线面角的三种求法1．直接法 ：平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。

通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。

例1 （ 如图1 ）四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。

（2）SC 与平面ABC 所成的角。

解:（1） ∵SC ⊥SB,SC ⊥SA,BMHSCA图1∴SC ⊥平面SAB 故 SB 是斜线BC 在平面SAB 上的射影， ∴∠SBC 是直线BC 与平面SAB 所成的角为60°。

（2） 连结SM,CM ，则SM ⊥AB,又∵SC ⊥AB,∴AB ⊥平面SCM, ∴面ABC ⊥面SCM过S 作SH ⊥CM 于H, 则SH ⊥平面ABC ∴CH 即为 SC 在面ABC 内的射影。

∠SCH 为SC 与平面ABC 所成的角。

sin ∠SCH=SH ／SC∴SC 与平面ABC 所成的角的正弦值为√7／7（“垂线”是相对的，SC 是面 SAB 的垂线，又是面 ABC 的斜线. 作面的垂线常根据面面垂直的性质定理，其思路是：先找出与已知平面垂直的平面，然后一面内找出或作出交线的垂线，则得面的垂线。

） 2. 利用公式sin θ=h ／ι其中θ是斜线与平面所成的角， h 是 垂线段的长，ι是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可用三棱锥的体积自等来求垂线段的长。

例2 （ 如图2） 长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ，求AB 与面 AB 1C 1D 所成的角。

解：设点 B 到AB 1C 1D 的距离为h, ∵V B ﹣AB 1C 1=V A ﹣BB 1C 1∴1／3 S △AB 1C 1·h= 1／3 S △BB 1C 1·AB ，易得h=12／5 设AB 与 面 A B 1C 1D 所成的角为θ,则sin θ=h ／AB=4／5A 1C 1D 1H4CB 123BAD图2∴AB 与面AB 1C 1D 所成的角为arcsin 4／5 3. 利用公式cos θ=cos θ1·cos θ2（如图3） 若 OA 为平面的一条斜线，O 为斜足，OB 为OA 在面α内的射影，OC 为面α内的一条直线，其中θ为OA 与OC 所成的角，B αOAC图3θ1为OA 与OB 所成的角，即线面角，θ2为OB 与OC 所成的角，那么 cos θ=cos θ1·cos θ2 （同学们可自己证明），它揭示了斜线和平面所成的角是这条斜线和这个平面内的直线所成的一切角中最小的角（常称为最小角定理）例3（如图4） 已知直线OA,OB,OC 两两所成的角为60°, ，求直线OA 与 面OBC 所成的角的余弦值。

第9节线面角及二面角的求法【基础知识】求线面角、二面角的常用方法：(1)线面角的求法，找出斜线在平面上的射影，关键是作垂线，找垂足，要把线面角转化到一个三角形中求解．(2）二面角的大小求法，二面角的大小用它的平面角来度量．： ]【规律技巧】平面角的作法常见的有①定义法；②垂面法．注意利用等腰、等边三角形的性质．【典例讲解】【例1】如图，在四棱锥P。

ABCD中，PA⊥底面ABCD，AB⊥AD,AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1）求PB和平面PAD所成的角的大小；(2)证明:AE⊥平面PCD；（3)求二面角A－PD－C的正弦值．（1)解在四棱锥P－ABCD中，因PA⊥底面ABCD，AB⊂平面ABCD，故PA⊥AB。

又AB⊥AD，PA∩AD＝A，从而AB⊥平面PAD,故PB在平面PAD内的射影为PA,从而∠APB为PB和平面PAD所成的角．在Rt△PAB中,AB＝PA，故∠APB＝45°.所以PB和平面PAD所成的角的大小为45°.(2)证明在四棱锥P－ABCD中，因PA⊥底面ABCD，CD⊂平面ABCD,故CD⊥PA.由条件CD⊥AC，PA∩AC＝A,∴CD⊥平面PAC。

又AE⊂平面PAC，∴AE⊥CD。

由PA＝AB＝BC,∠ABC＝60°，可得AC＝PA.∵E是PC的中点，∴AE⊥PC。

又PC∩CD＝C,综上得AE⊥平面PCD.【变式探究】如图所示，在四棱锥P－ABCD中,底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC.E是PC的中点，作EF⊥PB交PB于点F。

(1）证明PA∥平面EDB;(2)证明PB⊥平面EFD；（3）求二面角C－PB－D的大小．（1）证明如图所示,连接AC，AC交BD于O，连接EO.∵底面ABCD是正方形，∴点O是AC的中点．在△PAC中,EO是中位线，∴PA∥EO.而EO⊂平面EDB且PA⊄平面EDB，∴PA∥平面EDB.【针对训练】1．如图,四棱锥P－ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC＝2错误!，PA＝2,E 是PC上的一点,PE＝2EC。

线面角的求法总结（经典实用）
1、直接法：即定义法，做出斜线、垂线、斜线在平面上的射影组成的直角三角形,根据条件求出斜线与射影所成的角即为所求.
2、三余弦定理：设斜线与平面所成角为θ，在平面上作出一条过斜足的特殊直线,求出该直线与射影间的夹角θ，以及它与斜线间的夹角γ或其余弦,就可利用三余弦关系cosγ=cosθ·cosβ求出线面角的余弦值。

3、三正弦定理
设二面角M-AB-N的度数为α，在平面M内有一条射线AC，它和棱AB所成角为β，和平面N所成角为γ，则sinγ=sinαsinβ结论：二面角是半平面内的一条直线与另一半平面所成线面角的最大值，即二面角是线面角的最大值。

求线面角的方法引言求线面角是我们在数学中经常遇到的一个问题，它涉及到线与平面的交角，有着广泛的应用。

在实际问题中，求解线面角可以帮助我们计算光线的入射角、判断两个对象的相对位置等等。

本文将总结几种常见的方法来求解线面角，并进一步思考其应用。

1. 通过向量求解线面角以平面上一条直线与平面的交角为例，我们可以通过向量的夹角来求解线面角。

使用向量可以简化计算过程，并得到准确的结果。

首先，我们可以得到直线与平面的法向量，记为n，直线的方向向量，记为d。

然后，我们可以通过向量的内积公式（?·?=|?|·|?|·cos?）求得两个向量的夹角，即线面角。

具体计算方法如下：1.使用直线上两点的坐标差来计算直线的方向向量d；2.使用法线方程或者其他方法计算平面的法向量n；3.计算向量d和向量n的夹角，即可得到线面角。

举个例子，假设我们要求解直线L与平面P的交角，直线上两点的坐标分别为(x1, y1)和(x2, y2)，平面的法向量为(a, b, c)。

那么计算方法如下：1.方向向量d = (x2 - x1, y2 - y1)；2.计算法向量n = (a, b, c)；3.计算线面角的余弦值：cos? = d · n / (|d|·|n|)；4.求解弧度值：? = arccos(cos?)。

2. 利用平面方程求解线面角另一种常见的方法是利用平面的方程求解线面角。

通过平面的法向量和点到平面的距离，我们可以得到平面的方程，并利用方程求解线面角。

具体步骤如下：1.使用直线上两点的坐标差来计算直线的方向向量d；2.使用法线方程或者其他方法计算平面的法向量n；3.使用给定的点(x0, y0, z0)和法向量n计算平面的方程：ax + by + cz + d =0；4.通过点与平面的距离公式计算平面的距离：d = |ax0 + by0 + cz0 + d| /√(a^2 + b^2 + c^2)；5.计算线面角的余弦值：cos? = |d| / √(a^2 + b^2 + c^2)；6.求解弧度值：? = arccos(cos?)。

向量法求线面角公式
线面角是指由一条直线和一个平面所形成的角度。

通过向量法可以求出线面角的公式，具体如下：
假设直线的向量为 a，平面的法向量为 n，则线面角的大小可以通过向量点积计算：
cosθ = (a·n) / (|a||n|)
其中，|a|为向量 a 的模长，|n|为法向量 n 的模长，a·n 表示向量 a 和向量 n 的点积，θ 为线面角的大小。

通过反余弦函数可以求出线面角的弧度值，再将其转换为角度值即可得到最终的结果。

需要注意的是，在计算时需要确保直线和平面是在同一坐标系下表示的，且向量 a 与法向量 n 是互相垂直的。