专题3 空间垂直问题的证明方法-2019年高考数学考点讲解与真题分析

高中数学常见题型解法归纳 空间直线、平面垂直位置关系的证明【知识要点】一、空间直线、平面垂直位置关系的判定和证明空间直线、平面垂直位置关系的判定和证明一般有两种方法.方法一（几何法）：线线垂直⇔线面垂直⇔面面垂直，它体现的主要是一个转化的思想.方法二（向量法）：它体现的是数学的转化的思想和向量的工具性. 其中向量,a b 是直线,a b 的方向向量，且111222(,,),(,,)a x y z b x y z ==向量,m n 是平面,αβ的法向量，且333444(,,),(,,)m x y z n x y z ==1200(,1212z z a b a b a b x x y y a b a b +⊥⇔⊥⇔=⇔+=直线直线其中分别为直线，的方向向量）,,31313(1x y y z z a a m x a a m λλλαα===⊥⇔⇔直线平面其中为直线的方向向量,为平面的法向量）3400(3434z z m n m n x x y y m αβαβ+⊥⇔⊥⇔=⇔+=平面平面其中,n 分别为平面，的法向量） 二、空间的几何元素的位置关系从低到高有三个层次：线线关系、线面关系和面面关系.三、空间垂直位置关系的证明，总是把要证明的垂直关系首先转化成最靠近它的位置关系去证明.如果要证明线线垂直，只能首先转化成证明线面垂直；如果要证明线面垂直，可以首先转化成证明线线垂直或者面面垂直；如果要证明面面垂直，只能首先转化成证明线面垂直. 【方法讲评】【例1】【2017北京，文18】如图，在三棱锥P –ABC 中，PA ⊥AB ，PA ⊥BC ，AB ⊥BC ，PA =AB =BC =2，D 为线段AC 的中点，E 为线段PC 上一点．（Ⅰ）求证：PA ⊥BD ；（Ⅱ）求证：平面BDE ⊥平面PAC ； （Ⅲ）当PA ∥平面BD E 时，求三棱锥E –BCD 的体积．（III ）因为PA ∥平面BDE ，平面PAC平面BDE DE =，所以PA DE ∥.因为D 为AC 的中点，所以112DE PA ==，BD DC ==由（I ）知，PA ⊥平面ABC ，所以DE ⊥平面PAC .所以三棱锥E BCD -的体积1163V BD DC DE =⋅⋅=. 【点评】（1）本题的第1问证明PA ⊥BD ，转化成证明PA ⊥平面ABC ，第2问证明平面BDE ⊥平面PAC 转化成证明BD ⊥平面PAC .（2）空间垂直位置关系的证明，总是把要证明的垂直关系首先转化成最靠近它的位置关系去证明.转化成哪一条线垂直哪一条线，哪一条线垂直哪一个平面，哪一个平面垂直哪一个平面，这取决于你的观察和分析，主要关注已知条件中的有垂直关系的线和面.【例2】如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，60AB ADAC CD ABC ⊥⊥∠=，，°，PA AB BC ==，E 是PC 的中点．（Ⅰ）证明CD AE ⊥； （Ⅱ）证明PD ⊥平面ABE ；（Ⅲ）求二面角A PD C --的大小．（Ⅲ）ABCDPEABCDPEM⊥的关键是证明CD垂直AE所在的平面PCD.(2)证明PD⊥平面ABE的【点评】（1）证明CD AEPC CD关键是证明PD垂直平面ABE内的两条相交直线,.【反馈检测1】【2017课标3，理19】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C 的余弦值.【例3】如图，已知正方体1AC 棱长为2，E 、F 、G 分别是1CC 、BC 和CD 的中点. （1）证明：1A G ⊥面EFD ；（2）求二面角E DF C --的余弦值.(2)由(1)知1(2,1,2)AG =--为面EFD 的法向量 ∵CE ⊥面CFD ，(0,0,1)CE =为面CFD 的法向量 设1AG 与CE 夹角为θ，则11cos A G CE A G CEθ⋅==⋅231-⋅23=- 由图可知二面角E DF C --的平面角为πθ- ∴二面角E DF C --的余弦值为23. 【点评】本题由于是正方体，所以方便建立空间直角坐标系，所以选择向量的方法比较直接. 当然，也可以选择几何法.【反馈检测2】如图，已知多面体ABCDEF 中，ABCD 为菱形，60ABC ∠=︒，AE ⊥平面ABCD ，,1,AE CF AB AE AF BE ==⊥．（1）求证：AF ⊥平面BDE ；（2）求二面角F BE D --的余弦值．高中数学常见题型解法归纳及反馈检测第60讲： 空间直线、平面垂直位置关系的证明参考答案【反馈检测1答案】(1)证明略；.（2）由题设及（1）知，,,OA OB OD 两两垂直，以O 为坐标原点，OA 的方向为x 轴正方向，OA 为单位长，建立如图所示的空间直角坐标系O xyz -.则()()()()1,0,0,,1,0,0,0,0,1A B C D -.由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得12E ⎛⎫ ⎪ ⎪⎝⎭.故()()11,0,1,2,0,0,2AD AC AE ⎛⎫=-=-=- ⎪⎪⎝⎭.【反馈检测2答案】（1）见解析;(2）所求二面角得余弦值为5． 【反馈检测2详细解析】（1）设AC BD O ⋂=以O 为空间直角坐标系原点，以OB 为x +轴，以OC 为y +轴，以过O 点平行于AE 的射线为z +轴建立空间直角坐标系xOy ∵1AB AE ==，且菱形ABCD 中60ABC ∠=︒∴1110,,0,,0,,0,,0,,122222A B C D E ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ∵AECF 且()0,0,1AE =，∴设()()0,0,0CF λλ=> ∴10,,2F λ⎛⎫ ⎪⎝⎭又∵AF BE ⊥∴102AF BE λ⋅=-+=，∴12λ=，∴110,,22F ⎛⎫ ⎪⎝⎭又∵()10,1,02AF BD ⎛⎫⋅=⋅= ⎪⎝⎭∴AF BD ⊥，又AF BE ⊥且BD BE B = ∴AF ⊥平面BDE（2）设⊥m 平面BEF ，(),,x y z =m∴()11,,,1022BE x y z x y z ⎛⎫⋅=⋅-=-+= ⎪ ⎪⎝⎭m设所求二面角为θ，则有cosθ=.。

高考指南立体几何垂直证明的六大绝招秒懂！类型一AD⊥SC，求证:AD⊥面SBC证明：∵SA⊥面ABC ∴SA⊥BC又∠ACB=90°∴AC⊥BC又AC，SA⊆面SAC ∴BC ⊥面SAC∴BC⊥AD又AD⊥SC且BC，SC⊆面SBC∴AD⊥面SBC变式：如图，在三棱锥A-BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，求证：AD⊥AC类型二利用等腰三角形中线证垂直例题：在三棱锥P-ABC中，AC=BC，AP=BP，求证PC⊥AB证明：取AB的中点M，连接PM，CM∵AC=BC，M是AB的中点，∴AB⊥CM∵AP=BP，M是AB的中点，∴AB⊥PM∴AB⊥面PCM∴AB⊥PC变式：四棱锥P-ABCD，底面ABCD是正方形，PA=AD，求证面PAD⊥面PCD类型三利用勾股定理逆定理证垂直例题：如图，四棱锥P-ABCD的底面是边成为3的正方形，PA⊥CD，PA=4，PD=5，求证：PA⊥面ABCD证明：∵PA=4，AB=3，PD=5∴PA2+AB2=PD2，∴三角形PAD是直角三角形，∴PA⊥AD又PA ⊥CD，∴PA⊥面ABCD变式：如果，在三棱台ABC-DEF中，平面BDEF⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3，求证：BF⊥面ACFD类型四利用三角形全等证垂直例题：如图，三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°，求证：AB⊥PC证明：取AB的中点M，连接CM，∵△PAB是等边三角形，∴PB=PA又PC=PC，∠PAC=∠PBC=90°∴△PBC≌△PAC，∴BC=AC∴△ACB是等腰三角形，M是AB的中点，∴CM⊥AB又在等边△PAB中，M是AB的中点，∴PM⊥AB∴AB⊥面PMC∴AB⊥PC变式：如图，在以A、B、C、D、E、F为顶点的五面体中，平面CDEF⊥平面ABCD，FC=FB，四边形ABCD为平行四边形，且∠BCD=45°，求证：CD⊥BF类型五利用平行关系证明垂直例题：如图四棱锥P-ABCD，底面是正方形，PA⊥底面ABCD，∠PDA=45°，E是棱AB的中点，求证：面PCE⊥面PCD证明：分别做PC，PD的中点M，N两点，连接EM，MN，NA∵MN为△PCD的中位线，∴MN∥CD且MN=1/2CD又∵E是AB的中点，∴AE∥CD且AE=1/2CD ∴四边形AEMN是平行四边形，则EM∥AN，∵PA⊥面ABCD，∴PA⊥AD，且∠PDA=45°，∴△PAD 是等腰直角三角形又N是PD中点，∴AN⊥PD∵四边ABCD是正方形，∴CD⊥AD，又PA⊥CD，∴CD⊥面PAD，∴CD⊥AN，又上面已求PD⊥AN，∴AN⊥面PCD又∵EM∥AN，∴EM⊥面PCD∵EM ⊂面PEC，∴面PEC⊥面PCD变式：如图1，在直角梯形ABCD中，AD∥BC，∠BAD=90°，AB=BC=1，AD=2，E是AD的中点，O是AC与BE的交点，将△ABE沿BE折起到△A1BE的位置，如图2，证明CD⊥面A1OC.类型六梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2CD，侧面PBC⊥底面ABCD，证明：PA⊥BD。

专题32 空间中直线、平面垂直位置关系的证明方法【高考地位】立体几何是高考的重点内容之一，每年高考大题必有立体几何题，尤其是第一问主要考查证明线面垂直、平行，面面垂直等问题，解决这类问题的方法主要有：几何法和空间向量法. 在高考中其难度属中档题. 【方法点评】方法一 几何法使用情景：转化的直线或平面比较容易找到解题模板：第一步 按照线线垂直得到线面垂直，进而得出面面垂直的思路分析解答；第二步 找到关键的直线或平面； 第三步 得出结论.例1、【2018广西桂林市第十八中模拟】如图，在三棱锥P ABC -中， ,44CBA AB π∠===，,D E 分别为线段,AB BC 的中点， ,PD AC PE BC ⊥⊥.（1）求证： CD ⊥平面PAB ；（2）若F 为PA 上的点，且2,3C PEF PF FA V -==P 平面ABC 的距离.又∵,PD AC BC AC C ⊥⋂=，∴PD ⊥面ABC ， ∵CD ⊂面ABC ∴PD CD ⊥在ABC ∆中D 是AB 的中点， AC BC =，∴CD AB ⊥ ∵PD AB D ⋂=， ,PD AB ⊂面PAB ，∴CD ⊥平面PAB （2）由（1）知P 到面ABC 的距离为PD 由等体积知： 2233C PEF F PEC A PEC P AEC V V V V ----===∵3C PEF V -=2P AEC V -=∴123AEC PD S ∆⨯⨯⨯=∵122AEC S AC AE ∆=⨯⨯=， 1223PD ⨯⨯⨯=， ∴98PD =. 例2、如图所示，在四棱锥P ABCD -中，底面四边形ABCD 为等腰梯形，E 为PD 中点，PA ⊥平面ABCD ，//,,24AD BC AC BD AD BC ⊥==．证明：平面EBD ⊥平面PAC ； 【答案】详见解析线线垂直PA BD ⊥.试题解析：因为PA ⊥平面,ABCD BD ⊂平面ABCD ，所以PA BD ⊥，又因为,AC BD PA AC A ⊥=，所以BD ⊥平面PAC ，而BD ⊂平面EBD ，所以平面EBD ⊥平面PAC ． 考点：面面垂直判定定理【思路点睛】利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.【变式演练1】如图, 已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面, 平面ABCD平面ABPE AB =,且2,1,AB BP AD AE AE AB ====⊥,且AE BP . 设点M 为棱PD 中点, 在面ABCD 内是否存在点N ,使得MN ⊥平面ABCD ？若存在, 请证明, 若不存在, 说明理由。

2019年高考数学 专题32 空间中直线、平面垂直位置关系的证明方法黄金解题模板【高考地位】立体几何是高考的重点内容之一，每年高考大题必有立体几何题，尤其是第一问主要考查证明线面垂直、平行，面面垂直等问题，解决这类问题的方法主要有：几何法和空间向量法. 在高考中其难度属中档题.【方法点评】方法一 几何法使用情景：转化的直线或平面比较容易找到解题模板：第一步 按照线线垂直得到线面垂直，进而得出面面垂直的思路分析解答；第二步 找到关键的直线或平面；第三步 得出结论.例1、【2018广西桂林市第十八中模拟】如图，在三棱锥P ABC -中， ,44CBA AB π∠===，,D E 分别为线段,AB BC 的中点， ,PD AC PE BC ⊥⊥.（1）求证： CD ⊥平面PAB ；（2）若F 为PA 上的点，且2,3C PEF PF FA V -==P 平面ABC 的距离.又∵,PD AC BC AC C ⊥⋂=，∴PD ⊥面ABC ，∵CD ⊂面ABC ∴PD CD ⊥在ABC ∆中D 是AB 的中点， AC BC =，∴CD AB ⊥∵PD AB D ⋂=， ,PD AB ⊂面PAB ，∴CD ⊥平面PAB（2）由（1）知P 到面ABC 的距离为PD由等体积知： 2233C PEF F PEC A PEC P AEC V V V V ----===∵3C PEF V -=2P AEC V -=∴123AEC PD S ∆⨯⨯⨯=∵122AEC S AC AE ∆=⨯⨯=， 1223PD ⨯⨯⨯=， ∴98PD =. 例2、如图所示，在四棱锥P ABCD -中，底面四边形ABCD 为等腰梯形，E 为PD 中点，PA ⊥平面ABCD ，//,,24AD BC AC BD AD BC ⊥==．证明：平面EBD ⊥平面PAC ；【答案】详见解析线线垂直PA BD ⊥.试题解析：因为PA ⊥平面,ABCD BD ⊂平面ABCD ，所以PA BD ⊥，又因为,AC BD PA AC A ⊥=，所以BD ⊥平面PAC ，而BD ⊂平面EBD ，所以平面EBD ⊥平面PAC ．考点：面面垂直判定定理【思路点睛】利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.【变式演练1】如图, 已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面, 平面ABCD 平面ABPE AB =,且2,1,AB BP AD AE AE AB ====⊥,且AE BP . 设点M 为棱PD 中点, 在面ABCD 内是否存在点N ,使得MN ⊥平面ABCD ？若存在, 请证明, 若不存在, 说明理由。

空间几何中的垂线定理与推论在空间几何中，垂线定理与推论是重要的基础概念。

它们帮助我们理解不同几何形体之间的关系，探索空间中的垂直性质。

本文将详细介绍垂线定理与推论的概念、证明方法以及应用场景。

1. 垂线定理的定义与证明垂线定理是指：如果两条直线垂直于同一平面上的第三条直线，并且它们互相垂直，则这两条直线平行。

该定理在解决空间中直线和平面相互垂直的问题时起到了关键作用。

假设在空间中有三条直线，分别为AB、CD和EF。

已知CD⊥EF，且AB⊥CD，我们需要证明AB∥EF。

证明过程：首先，在CD上找一点O，使得AO⊥CD。

根据垂线定义，我们知道AO与CD垂直。

然后，连接BO并假设BO与EF相交于点N。

根据角的性质，我们得到∠NOB=90°。

此外，由于AB⊥CD，所以∠BAO=90°。

根据传递性质，我们可以得出∠BAO=∠NOB。

因此，可得到AO∥BO。

接下来，我们需要证明EF⊥BO。

由于FO⊥CD，所以FO⊥BO。

此外，根据垂线定理的定义，我们知道AO∥BO，因此，可得到EF⊥BO。

根据垂线定理，我们可以得出AB∥EF。

2. 垂线推论的应用垂线定理还引申出许多有用的推论，这些推论广泛应用于几何学的各个领域。

下面列举了几个常见的垂线推论及其应用。

推论1：如果两条直线垂直于同一平面上的某条直线，它们互相垂直。

应用：在解决平面几何问题时，可以利用该推论判断两条直线是否垂直。

推论2：如果两条直线分别与同一直线垂直，并且它们不相交，则它们平行。

应用：在平面几何中，该推论帮助我们判定两条直线是否平行。

推论3：如果两个平面互相垂直，则它们的交线是一条直线。

应用：该推论在解决空间几何问题时非常有用，可以帮助我们找到两个垂直平面的交线。

推论4：如果两条直线分别与同一平面垂直，并且它们不在同一直线上，则它们平行于平面。

应用：该推论在解决空间几何问题中帮助我们判断直线与平面之间的关系。

3. 垂线定理与推论的应用举例垂线定理与推论不仅具有理论意义，还广泛应用于实际问题中。

空间几何垂直的判定定理公式在我们学习数学的漫漫征途中，空间几何垂直这一板块就像是一座神秘的城堡，而垂直的判定定理公式则是打开城堡大门的神奇钥匙。

咱们先来说说线面垂直的判定定理。

如果一条直线与一个平面内的两条相交直线都垂直，那么这条直线就与这个平面垂直。

这就好比在操场上，有一根旗杆直直地立在地面上。

假设地面是一个平面，而在地面上有两条相交的跑道线，这根旗杆和这两条跑道线都相互垂直，那这旗杆肯定就和整个地面垂直啦！再看看面面垂直的判定定理，如果一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直。

这就好像是两块相邻的木板，一块木板垂直地靠在另一块木板上，那这两块木板所在的平面自然就是垂直的关系。

还记得我之前教过的一个学生小明，他一开始对这些判定定理那叫一个头疼，总是搞混。

有一次做作业，碰到一个证明线面垂直的题目，他想都不想就乱写一通，结果当然是错得一塌糊涂。

我就问他：“小明啊，你想想那个操场上的旗杆，是不是得和两条相交的跑道线都垂直才能立稳呀？”小明眨眨眼，好像突然开窍了。

从那以后，他每次遇到这类问题，都会在脑海里想象那个画面，做题的准确率也越来越高。

其实啊，这些判定定理并不是什么高深莫测的东西。

咱们只要多联系实际，多做几道题，就能把它们掌握得牢牢的。

比如说，家里的墙角，是不是就是三条线两两垂直，从而形成了三个相互垂直的面？还有，建筑工地上的塔吊，那长长的吊臂和塔身是不是也存在着垂直的关系？在解决空间几何垂直问题的时候，咱们要善于从生活中寻找例子，把抽象的定理具体化。

这样一来，不仅能让我们更好地理解和记忆这些定理，还能提高我们解决问题的能力。

对于线线垂直的判定，也有一些小窍门。

如果一条直线垂直于一个平面，那么这条直线垂直于平面内的任意一条直线。

这就好比你手里拿着一根垂直于桌面的铅笔，那这根铅笔是不是和桌面上的所有直线都垂直呀？还有一种情况，如果两条平行线中的一条垂直于一条直线，那么另一条也垂直于这条直线。

1．以立体几何的定义、公理和定理为出发点，认识和理解空间中线、面垂直的有关性质与判定定理。

2．能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题。

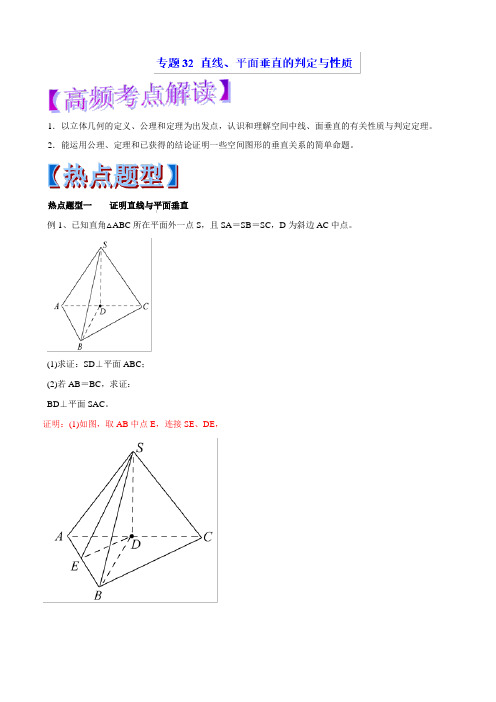
热点题型一证明直线与平面垂直例1、已知直角△ABC所在平面外一点S，且SA＝SB＝SC，D为斜边AC中点。

(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC。

证明：(1)如图，取AB中点E，连接SE、DE，∴BD ⊥平面SAC 。

方法二，若AB ＝BC ，则BD ⊥AC 。

由(1)知SD ⊥平面ABC ，又SD ⊂平面SAC ， ∴平面ABC ⊥平面SAC ，又平面ABC∩平面SAC ＝AC 。

∴BD ⊥平面SAC 。

【提分秘籍】证明线面垂直的常用方法 (1)利用线面垂直的判定定理。

(2)利用“两平行线中的一条与平面垂直，则另一条也与这个平面垂直”。

(3)利用“一条直线垂直于两个平行平面中的一个，则与另一个也垂直”。

(4)利用面面垂直的性质定理。

【举一反三】如图所示，已知AB 为圆O 的直径，点D 为线段AB 上一点，且AD ＝13DB ，点C 为圆O 上一点，且BC ＝3AC ，PD ⊥平面ABC ，PD ＝DB 。

求证：PA⊥CD。

解析：因为AB为圆O的直径，所以AC⊥CB，在Rt△ABC中，由3AC＝BC得，∠ABC＝30°，热点题型二证明平面与平面垂直例2、（2018年江苏卷）在平行六面体中，．求证：（1）；（2）．【答案】答案见解析【解析】所以AB1⊥平面A1BC．因为AB1平面ABB1A1，所以平面ABB1A1⊥平面A1BC．【变式探究】如图所示，已知△ABC是等边三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、DB在平面ABC 的同侧，M为EA的中点，CE＝2BD，求证：(1)平面BDM⊥平面ECA；(2)平面DEA⊥平面ECA。

∴平面BDM⊥平面ECA。

(2)∵MD⊥平面ECA，MD⊂平面DEA，∴平面DEA⊥平面ECA。

2019年高考数学（文）热点题型和提分秘籍1．在空间中，l，m，n，a，b表示直线，α表示平面，则下列命题正确的是()A．若l∥α，m⊥l，则m⊥αB．若l⊥m，m⊥n，则m∥nC．若a⊥α，a⊥b，则b∥αD．若l⊥α，l∥a，则a⊥α【答案】D2．已知平面α与平面β相交，直线m⊥α，则()A．β内必存在直线与m平行，且存在直线与m垂直B．β内不一定存在直线与m平行，不一定存在直线与m垂直C．β内不一定存在直线与m平行，但必存在直线与m垂直D．β内必存在直线与m平行，不一定存在直线与m垂直【解析】如图，在平面β内的直线若与α，β的交线a平行，则有m与之垂直．但却不一定在β内有与m平行的直线，只有当α⊥β时才存在。

9．设a，b是夹角为30°的异面直线，则满足条件“a⊂α，b⊂β，且α⊥β”的平面α，β()A．不存在B．有且只有一对C．有且只有两对 D．有无数对【答案】D10．如图7-5-10，在正方形ABCD中，E、F分别是BC、CD的中点，G是EF的中点，现在沿AE、AF及EF 把这个正方形折成一个空间图形，使B、C、D三点重合，重合后的点记为H，那么，在这个空间图形中必有()图7-5-10A．AG⊥平面EFH B．AH⊥平面EFHC．HF⊥平面AEF D．HG⊥平面AEF【答案】B【解析】根据折叠前、后AH⊥HE，AH⊥HF不变，∴AH⊥平面EFH，B正确；∵过A只有一条直线与平面EFH垂直，∴A不正确；∵AG⊥EF，EF⊥GH，AG∩GH＝G，∴EF⊥平面HAG，又EF⊂平面AEF，∴平面HAG⊥AEF，过H作直线垂直于平面AEF，一定在平面HAG内，∴C不正确；由条件证不出HG⊥平面AEF，∴D不正确．故选B.11．如图7-5-11，∠BAC＝90°，PC⊥平面ABC，则在△ABC，△P A C的边所在的直线中，与PC垂直的直线是________；与AP垂直的直线是________．图7-5-11【答案】AB，BC，AC；AB12．如图7-5-12所示，在四棱锥P-ABCD中，P A⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)图7-5-12【答案】DM⊥PC(或BM⊥PC)【解析】连接AC，BD，则AC⊥BD，∵P A⊥底面ABCD，∴P A⊥BD.又P A∩AC＝A，∴BD⊥平面P AC，∴BD⊥PC．∴当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD.而PC⊂平面PCD，∴平面MBD⊥平面PCD.13．α，β是两个平面，m，n是两条直线，有下列四个命题：①如果m⊥n，m⊥α，n∥β，那么α⊥β.②如果m⊥α，n∥α，那么m⊥n.③如果α∥β，m⊂α，那么m∥β.④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．其中正确的命题有________．(填写所有正确命题的编号)【答案】②③④14.如图7-5-16，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，底面是以∠ABC为直角的等腰直角三角形，AC＝2a，BB1＝3a，D是A1C1的中点，点F在线段AA1上，当AF＝________时，CF⊥平面B1DF.图7-5-16【答案】a或2a【解析】∵B1D⊥平面A1ACC1，∴CF⊥B1D.为了使CF⊥平面B1DF，只要使CF⊥DF(或CF⊥B1F)．设AF＝x，则CD2＝DF2＋FC2，∴x2－3ax＋2a2＝0，∴x＝a或x＝2a.【答案】216．在△ABC中，∠ACB＝90°，AB＝8，∠ABC＝60°，PC⊥平面ABC，P C＝4，M是AB上一个动点，则PM的最小值为__________。

立体几何垂直证明题常见模型及方法证明空间线面垂直需注意以下几点：①由已知想性质，由求证想判定，即分析法与综合法相结合寻找证题思路。

②立体几何论证题的解答中，利用题设条件的性质适当添加辅助线（或面）是解题的常用方法之一。

③明确何时应用判定定理，何时应用性质定理，用定理时要先申明条件再由定理得出相应结论。

垂直转化：线线垂直 线面垂直 面面垂直；基础篇类型一：线线垂直证明（共面垂直、异面垂直）（1） 共面垂直：实际上是平面内的两条直线的垂直 （只需要同学们掌握以下几种模型）○1 等腰（等边）三角形中的中线○2 菱形（正方形）的对角线互相垂直 ○3勾股定理中的三角形 ○4 1:1:2 的直角梯形中 ○5 利用相似或全等证明直角。

例：在正方体1111ABCD A B C D -中，O 为底面ABCD 的中心，E 为1CC ,求证：1A O OE ⊥（2） 异面垂直 （利用线面垂直来证明，高考中的意图） 例1 在正四面体ABCD 中，求证AC BD ⊥变式 1 如图，在四棱锥ABCD P -中，底面ABCD 是矩形，已知60,22,2,2,3=∠====PAB PD PA AD AB ．证明：AD PB ⊥；变式2 如图，在边长为2的正方形ABCD 中，点E 是AB 的中点，点F 是BC 的中点，将△AED,△DCF 分别沿,DE DF 折起，使,A C 两点重合于'A . 求证:'A D EF ⊥；变式3如图，在三棱锥P ABC -中，⊿PAB 是等边三角形，∠P AC =∠PBC =90 º证明：AB ⊥PC类型二：线面垂直证明方法○1 利用线面垂直的判断定理例2：在正方体1111ABCD A B C D -中，O 为底面ABCD 的中心，E 为1CC ,求证：1A O BDE ⊥平面变式1：在正方体1111ABCD A B C D -中，,求证：11AC BDC ⊥平面 变式2：如图：直三棱柱ABC －A 1B 1C 1中， AC =BC =AA 1=2，∠ACB =90︒.E 为BB 1的中点，D 点在AB 上且DE = 3 . 求证：CD ⊥平面A 1ABB 1；BE'ADFG变式3：如图，在四面体ABCD 中，O 、E 分别是BD 、BC 的中点，变式4 如图，在底面为直角梯形的四棱锥P ABCD -中，AD BC ∥，90ABC ∠=°，PA ⊥平面ABCD ．3PA =，2AD =，AB =6BC =C类型3：面面垂直的证明。

高中数学专题讲座垂直问题1、空间的垂直关系总论 (2)2、直线与直线垂直 (2)3、直线与平面垂直 (4)（1）直线与平面垂直的定义 (4)（2）直线与平面垂直的判定定理 (4)3．平面与平面垂直 (6)（1）平面与平面垂直的判定定理 (6)（2）平面与平面垂直的性质定理 (7)1、空间的垂直关系总论空间的垂直关系：线⊥线 −−−→←−−−判定性质 线⊥面 −−−→←−−−判定性质 面⊥面可见垂直关系的基础是线线垂直2、直线与直线垂直空间两条直线垂直包括两种情况——相交（共面）垂直和异面垂直,均可用a b ⊥表示. 要证明空间两条直线（线段）垂直，首先判断两直线是相交还是异面：1、若两直线是相交的，往往借助平面几何的一些性质，如：（1）等腰三角形底边上的中线与底边垂直；（2）直角三角形；法1：勾股定理，法2：若一个三角形一边上的中线长等于该边的一半则为直角三角形；（3）矩形，正方形，菱形自身的属性；（4）直径所对的圆周角为直角;（5）一些特殊平面图形的几何特征：模型1: 长宽比为例 矩形ABCD 中，1AD =，DC =，E 是DC 的中点，下面证明AE ⊥BD:tan tan 22DE BC EAD BDC AD DC ∠==∠== 所以EAD BDC ∠=∠，故AE BD ⊥模型2：长宽比为1:2的长方形模型3:边长为112的直角梯形模型4：内角为60°的菱形2、若两条直线是异面的，则需要利用空间的一些特殊方法；（1）a b ⊥，//b c ⇒a c ⊥；（2）a ⊥（b 所在的一个平面）⇒a b ⊥；两个重要模型：（1） 三垂线定理直线b 是平面的一条斜线，即与平面α相交但不垂直，直线c 在平面α内，因为a ⊥平面α，则a ⊥c ；若m ⊥c ，则因为a ，m 是相交直线，则c ⊥平面β，于是c ⊥b（这个定理最重要的应用在于，证明平面内的一条直线与平面的一条斜线垂直，尤其是二者是异面直线时）应用举例：正方体中，求证：1BD AC ⊥（2） 双等腰模型已知：,AM AN BM BN == ，求证：AB MN ⊥证明：取MN 的中点为O ，连接AO,BO ，在因为,AM AN BM BN ==，则AO ⊥MN ，BO ⊥MN ，又AO ∩BO=O ，则MN ⊥平面AOB ，于是AB MN ⊥3、直线与平面垂直（1）直线与平面垂直的定义是指直线与平面任何一条(所有)直线垂直，a a αα⊥⇔⊥平面内任意直线平面知道下面两个事实：过一点有且只有一条直线和一个平面垂直，过一点有且只有一个平面和一条直线垂直.（2）直线与平面垂直的判定定理法1：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面.即 ,,l b l aa b l a b O αα⊥⊥⎫⎪⊂⇒⊥⎬⎪=⎭平面平面简记为“线线垂直⇒线面垂直”法2：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.例1 已知P A ⊥⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上任意一点（不同于,A B ），（1）求证：BC ⊥平面P AC .（2）过A 点作AE ⊥PC 于点E ，求证：AE ⊥平面PBC .证明：（1）∵P A ⊥平面ABC ，∴P A ⊥BC .又∵AB 是⊙O 的直径，∴BC ⊥AC .而P A ∩AC =A ，∴BC ⊥平面P AC .（2）在（1）中已证BC ⊥平面P AC .又∵AE 在平面P AC 内，∴BC ⊥AE .∵PC ⊥AE ，且PC ∩BC =C ，∴AE ⊥平面PBC .例 如图, PA ⊥矩形ABCD 所在的平面，,M N 分别是AB 、PC 的中点．求证：MN AB ⊥；证法1：证明AB ⊥MN 所在的一个平面即可；连AC ，取AC 中点E ，连,ME NE ，则NE ∥PA ，∵PA ⊥平面ABCD ，∴ NE ⊥平面ABCD ，∴NE ⊥AB ，在△ABC 中，ME 是中位线，故ME ⊥AB ，ME ∩NE=E ，所以AB ⊥平面MNE,∴MN ⊥AB ．证法2：取DC 的中点E ，去证明AB ⊥平面NME 即可【思路2】：注意到AB 与MN 是相交的，可以考虑利用平面几何的方法，产生下面的解法证法3：因为MN 与AB 相交，E 是中点，所以可以考虑用“等腰三角形底边上的中线与底边垂直”这个方法；连,,.AC AN NB PB ,∵PA ⊥平面ABCD ，∴PA BC ⊥，又AB BC ⊥,∴BC ⊥平面PAB;∴BC ⊥PB那么在直角△PBC 中，NB=½PC ，在直角△PAC 中，AN=½PC;∴AN=NB∴MN ⊥AB4．平面与平面垂直（1）平面与平面垂直的判定定理若一个平面内有一条直线与另一个平面垂直，则这两个平面互相垂直 l a l αββ⊥⎫⇔⊥⎬⊂⎭平面平面可见，证明面面垂直的关键还是线面垂直，归根结底是线线垂直！例 如图所示，△ABC 所在平面外一点S ，且SA SC =，BA=BC ，点D 为AC 的中点.求证：平面SBD ⊥平面SAC ；分析：在两个三角形平面内寻找，哪条线垂直于另外的平面，逐个扫描，如果有现成的自然好，若没有，则考虑做辅助线；证明：因为SA=SC ，D 为AC 的中点， 所以SD ⊥AC.连接BD. 在△ABC 中，∵BA=BC ，所以 BD ⊥AC.又SD ∩BD=D ，所以AC ⊥平面ABC ，又AC ⊂平面SAC;所以平面SBD ⊥平面SAC ；例 （呼市2014届一模） 四棱锥P-ABCD 的底面ABCD 为菱形，PD ⊥平面ABCD ，PD=AB=2，角BAD=60°，E,F 分别为BC ，PA的中点，（1） 求证：平面DEF ⊥平面PAD（2） 求平面PDE 与平面PAB 所成二面角的正弦值解：（1）连接BD ，在△BDC 中，BD=DC=BC ，又E 为BC 的中点，故DE ⊥BC ，而AD ∥BC ，于是AD ⊥DE ；又PD ⊥平面ABCD ，于是PD ⊥DE ；PD ∩DA=D,所以DE ⊥平面PAD ， 则PD ⊥DE ，PD=AD，F为PA的中点，则PA⊥FD，于是PA⊥平面FDE，PA在平面PAD内，所以平面PDE⊥平面PAD【技巧总结】要证明面面垂直，关键是在一个面内找到另一个面的垂线，注意到此时两个平面一定是相交的，所以，我们先找到交线，然后，先逐条扫描每个面内的线是否可能垂直交线，我们遇到的问题中，平面多用三角形或四边形表示，因此这个扫描的工作量是不大的，如果现成的线中没有，就考虑做辅助线。

空间几何的证明方法空间几何是研究点、线、面和立体等几何图形之间的相互关系和性质的数学学科。

证明是数学学科中重要的思维方法之一，通过证明可以推理出几何问题的解决方案。

本文将介绍一些常用的空间几何的证明方法，帮助读者更好地理解几何问题。

一、直线的垂直性证明方法在空间几何中，直线的垂直性是一个基本的概念。

直线A和直线B 互相垂直的证明方法可以采用以下步骤：1. 通过测量或给出直线A和直线B的斜率，判断直线A和直线B 是否互相垂直。

2. 在给出直线A和直线B的坐标系中，通过计算两条直线之间的夹角，以判断直线A和直线B是否互相垂直。

3. 如果直线A和直线B的斜率或夹角满足一定条件（如斜率的乘积等于-1），则可以推论直线A和直线B互相垂直。

二、平面的平行性证明方法在空间几何中，平面的平行性是一个重要的性质。

平面A和平面B 互相平行的证明方法可以采用以下步骤：1. 给出两个平面的方程，通过比较两个平面的法向量，判断平面A 和平面B是否互相平行。

2. 给出两个平面的法向量和一个共面点，通过计算两个法向量的向量积，以判断平面A和平面B是否互相平行。

3. 如果两个平面的法向量相等或平行，并且一个共面点在另一个平面上，则可以推论平面A和平面B互相平行。

三、立体的相似性证明方法在空间几何中，立体的相似性是用来描述两个立体形状相似程度的性质。

立体A和立体B相似的证明方法可以采用以下步骤：1. 给出立体A和立体B的形状特征，通过比较两个立体的边长、面积和体积，判断立体A和立体B是否相似。

2. 给出立体A和立体B的顶点坐标，通过计算两个立体的相对位置和形状变换，以判断立体A和立体B是否相似。

3. 如果两个立体的形状特征满足一定条件（如边长之比相等等），则可以推论立体A和立体B相似。

四、圆锥的相似性证明方法在空间几何中，圆锥的相似性是描述两个圆锥形状相似程度的性质。

圆锥A和圆锥B相似的证明方法可以采用以下步骤：1. 给出圆锥A和圆锥B的形状特征，通过比较两个圆锥的高度、底面半径和斜高，判断圆锥A和圆锥B是否相似。

立体几何中垂直证明一、 “垂直关系”常见证明方法1直线与直线垂直的证明1.1 利用某些平面图形的特性：如直角三角形的两条直角边互相垂直,等边、等腰三角形（中线即高线），正方形、矩形邻边垂直，正方形菱形对角线垂直等。

1.2 看夹角：两条共（异）面直线的夹角为90°，则两直线互相垂直。

1.3 利用直线与平面垂直的性质：如果一条直线与一个平面垂直，则这条直线垂直于此平面内的所有直线。

1.4 利用平面与平面垂直的性质推论：如果两个平面互相垂直，在这两个平面内分别作垂直于交线的直线，则这两条直线互相垂直。

1.5 利用常用结论：① 如果两条直线互相平行，且其中一条直线垂直于第三条直线，则另一条直线也垂直于第三条直线。

② 如果有一条直线垂直于一个平面，另一条直线平行于此平面，那么这两条直线互相垂直。

2 直线与平面垂直的证明2.1 利用某些空间几何体的特性：如长方体侧棱垂直于底面 等2.2 看直线与平面所成的角：如果直线与平面所成的角是直角，则这条直线垂直于此平面。

2.3 利用直线与平面垂直的判定定理：bβαlb l a b a l ⊥⊥⊂⊂=⋂⊥βαβαβαba ⊥⇒ca ba ⊥∥cb ⊥⇒baαcabαα⊥⊂b a ab ⊥⇒αb αα∥b a ⊥ba ⊥⇒一条直线与一个平面内的两条相交直线都垂直，则该直线垂直于此平面。

2.4 利用平面与平面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。

2.5 利用常用结论：① 一条直线平行于一个平面的一条垂线，则该直线也垂直于此平面。

② 两个平面平行，一直线垂直于其中一个平面，则该直线也垂直于另一个平面。

3 平面与平面垂直的证明3.1 利用某些空间几何体的特性：如长方体侧面垂直于底面等3.2 看二面角：两个平面相交，如果它们所成的二面角是直二面角（即平面角是直角的二面角），就说这连个平面互相垂直。

3.3 利用平面与平面垂直的判定定理一个平面过另一个平面的垂线，则这两个平面垂直。

(高考冲刺押题)2019高考数学三轮基础技能闯关夺分必备空间中的垂直关系（含解析）【考点导读】1、掌握直线与平面、平面与平面垂直的判定定理和性质定理，并能用它们证明和解决有关问题。

2、线面垂直是线线垂直与面面垂直的枢纽，要理清楚它们之间的关系，学会互相转化，善于利用转化思想。

【基础练习】1、“直线l 垂直于平面α内的无数条直线”是“l α⊥”的 必要 条件。

2、如果两个平面同时垂直于第三个平面，那么这两个平面的位置关系是 平行或相交 。

3、、αβ是两个平面，直线,.l l αβ⊄⊄假设以①l α⊥，②//l β，③αβ⊥中两个为条4、在正方体中，与正方体的一条对角线垂直的面对角线的条数是6。

5、两个平面互相垂直，一条直线和其中一个平面平行，那么这条直线和另一个平面的位置关系是平行、相交或在另一个平面内。

6、在正方体1111ABCD A B C D -中，写出过顶点A 的一个平面__AB 1D 1_____，使该平面与正方体的12条棱所在的直线所成的角均相等(注：填上你认为正确的一个平面即可，不必考虑所有可能的情况)。

【范例导析】例1、如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F .〔1〕证明PA //平面EDB ；〔2〕证明PB ⊥平面EFD ；解析：本小题考查直线与平面平行,直线与平面垂直基础知识,考查空间想象能力和推理论证能力.证明：〔1〕连结AC ,AC 交BD 于O ,连结EO .∵底面ABCD 是正方形,∴点O 是AC 的中点在PAC ∆中,EO 是中位线,∴PA //EO而⊂EO 平面EDB 且⊄PA 平面EDB ,【反馈演练】 1、以下命题中错误的选项是〔3〕。

〔1〕假设一直线垂直于一平面，那么此直线必垂直于这一平面内所有直线〔2〕假设一平面经过另一平面的垂线，那么两个平面互相垂直 〔3〕假设一条直线垂直于平面内的一条直线，那么此直线垂直于这一平面 〔4〕假设平面内的一条直线和这一平面的一条斜线的射影垂直，那么它也和这条斜线垂直2、设z y x ,,是空间的不同直线或不同平面，且直线不在平面内，以下条件中能保证“假设 z x ⊥，且y x z y //,则⊥”为真命题的是①③④〔填所有正确条件的代号〕①x 为直线，y ，z 为平面②x ，y ，z 为平面 ③x ，y 为直线，z 为平面④x ，y 为平面，z 为直线 ⑤x ，y ，z 为直线3、二面角α—a —β的平面角为120°，在面α内，AB ⊥a 于B ，AB=2在平面β内，CD ⊥a 于D ，CD=3，BD=1，M 是棱a 上的一个动点，那么AM+CM 的最小值为26 。

一、考点简介线面关系是立体几何中的一种重要关系，在高考中几乎每年都会考查，且常以多面体为背景。

1、高考始终把直线与平面平行（垂直）的性质与判定和平面与平面平行（垂直）的判定与性质作为考查的重点，常以棱柱、棱锥为背景设计命题。

转化法是空间中垂直（平行）关系的重要数学方法，证明面面垂直（平行），则需要转化为线面垂直（平行）；而证明线面垂直（平行），则需要转化为线线垂直（平行）。

通过这一转化能够给某些有关空间中垂直关系的问题巧妙地创造条件。

近几年以探索性问题考查线面、面面关系是考查热点，如探索点的存在性、探索点的位置等是命题热点。

2、空间的角度与距离知识的考查形式既有选择题与填空题，有时又会出现解答题。

特别是异面直线所成角，直线与平面所成的角，二面角以及两点间的距离，点到平面的距离等，都是命题的重要内容。

高考中常把空间角与距离综合在一起，以解答题的形式考查，通常情况下，这类问题都可以用两种解法，即传统法与向量法，其中向量法更简单。

二、考点例析1、点、线、面之间位置关系例1、若l m n ，，是互不相同的空间直线，αβ，是不重合的平面，则下列命题中为真命题的是（ ） Ａ．若l n αβαβ⊂⊂，，∥，则l n ∥ Ｂ．若l αβα⊥⊂，，则l β⊥ Ｃ．若l n m n ⊥⊥，，则l m ∥Ｄ．若l l αβ⊥，∥，则αβ⊥解：两面平行，两面中的直线不一定都互相平行，因此A 不对；两面垂直，一个面内的直线不一定垂直于另一个平面，因此B 不对；在空间中垂直于同一直线的两直线，未必垂直，因此C 不对；故选D.点评：本题考查了考生对空间点、线、面的平行与垂直关系的空间想象能力及对其位置关系的理论推导，同时也考查了考生将几何语言、符号语言、图形语言进行转化与利用的能力，及灵活选择不同的信息条件进行解题的信息处理与分析能力。

例2、给出下列命题：（1）若平面α上的直线a 与平面β上的直线b 为异面直线，直线c 是α与β的交线，那么c 至多与a 、b 中一条相交；（2）若直线a 与b 异面，直线b 与c 异面，则直线a 与c 异面；（3）一定存在平面γ同时和异面直线a 、b 都平行，其中正确命题为（ ） A 、（1） B 、（2） C 、（3） D 、（4）解：（1）错，c 可与a 、b 中的两条相交；（2）错，因a 、c 可能相交也可能平行；（3）对，例如：过异面直线a 、b 的公垂线段的中点且与公垂线垂直的平面即可满足条件，因此选C.点评：此题考查了异面直线的性质，除以上的几个方面之外，还有以下结论：过两异面直线中一条有且只有一个平面与另一条直线平行；过不在两异面直线上空间任一点与两异面直线都相交的直线有一条或不存在；两异面直线的公垂线有且只有一条等。

高中数学空间直线、平面垂直的判定及其性质解析！一、直线和平面垂直的判定和性质1、证明直线和平面垂直的常用方法：① 利用判定定理；② 利用平行线垂直于平面的传递性（a∥b , a⊥α，则b⊥α .）;③ 利用面面平行的性质（a⊥α，α∥β , 则a⊥β .）;④ 利用面面垂直的性质 .注：当直线和平面垂直时，该直线垂直于平面内的任何一条直线，常用来证明线线垂直 .【例题1】如图所示，已知 PA 垂直于矩形 ABCD 所在的平面，点 M , N 分别是 AB , PC 的中点，若∠PDA = 45°，求证：MN⊥平面 PCD .例题1图【解析】思路：点 M , N 是中点，取 PD 中点 E，则MN∥AE ,AE⊥平面 PCD，则MN⊥平面 PCD .解答：证明：如下图所示，取 PD 的中点 E，连接 AE , NE .∵ 点 E , N 分别为 PD , PC 的中点，∴ EN∥且= 1/2 CD , (三角形中位线定理)又∵ 点 M 是 AB 的中点，四边形 ABCD 为矩形，∴ AM ∥且= 1/2 CD ,∴ EN ∥且= AM，∴ 四边形 AMNE 为平行四边形 .∴ MN ∥且= AE ,又∵ PA⊥平面 ABCD，∠PDA = 45°，∴ △PAD 为等腰直角三角形，∴ AE⊥PD .又∵ CD⊥AD，CD⊥PA，∴ CD⊥平面 PAD , 而 AEㄷ平面 PAD ,∴ CD⊥AE .又∵ CD∩PD = D ,∴ AE⊥平面 PCD ，∴MN⊥平面 PCD .二、平面与平面垂直的判定1、证明面面垂直的常用方法：① 利用判定定理；（判断垂线常用等腰三角形“三线合一”、“勾股定理”等结论 .）② 利用定义证明；（判断两平面所成的二面角是直二面角 .）③ 利用常用结论；（若α∥β，α⊥γ，则有β⊥γ .）【例题2】如图所示，在直三棱柱 ABC-A1B1C1 中，AB = BC , 点 D 是 AB 的中点 .(1) 求证：BC1∥平面 CA1D ;(2) 求证：平面CA1D⊥平面 AA1B1B .例题2图【解析】思路：(1) 连接 AC1 交 A1C 于点 E，连接 DE，则 E 为中点，则DE∥BC1 , 所以BC1∥平面 CA1D ; （DE 是△ABC1 的中位线）(2) AC = BC , 则AB⊥CD（等腰三角形中“三线合一”），A1A⊥平面 ABC 则A1A⊥CD , 则CD⊥平面 A1ABB1 ,所以平面CA1D⊥平面 AA1B1B .解答：(1)证明：如下图所示，连接 AC1 交 A1C 于点 E，连接 DE ，∵ 四边形 AA1C1C 为矩形，∴ 点 E 为对角线 AC1 的中点，又∵ 点 D 是 AB 的中点，∴ DE 为△ABC1 的中位线，∴ DE∥BC1，又∵ DEㄷ平面 CA1D , BC1 不ㄷ平面 CA1D，∴ BC1∥平面 CA1D .(2) 证明：∵ AC = BC , 点 D 为 AB 的中点，∴ CD⊥AB，又∵ A1A⊥平面 ABC，CDㄷ平面 ABC，∴ A1A⊥CD，∵ A1A∩AB = A，∴ CD⊥平面 A1ABC1 ,又∵ CDㄷ平面 CA1D ,∴ 平面CA1D⊥平面 AA1B1B .三、平面与平面垂直性质的应用① 当两个平面垂直时，把面面垂直转化为线面垂直，从而在证明线线垂直 .常作的辅助线是在其中一个平面内作两平面交线的垂线 .② 已知面面垂直，通过作辅助线转化为线面垂直，从而有更多的线线垂直的条件可用 .通过证线面垂直来证线线垂直是空间中证明两直线垂直最常用的方法 .【例题3】如图所示，在四棱锥P-ABCD 中，平面PAD⊥平面ABCD，AB∥CD，△PAD 是等边三角形，已知 BD = 2AD = 8 , AB = 2CD = 4√5 .(1) 设 M 是 PC 上的一点，证明：平面MBD⊥平面 PAD；(2) 求四棱锥 P-ABCD 的体积 .例题3图思路：(1) 因为两平面垂直与点 M 的位置无关，所以在平面 MBD 中，一定有直线垂直于平面 PAD，猜想来证明BD⊥平面 PAD .(2) 四棱锥底面 ABCD 为一梯形，高为点 P 到平面 ABCD 的距离 .解答：(1) 证明：在△ABD 中，∵ AD = 4 , BD = 8 , AB = 4√5 ,∴ AD^2 + BD^2 = AB^2 ,∴ AD⊥BD，又∵ 平面PAD⊥平面 ABCD，平面PAD∩平面 ABCD = AD，∴ BD⊥平面 PAD，又∵ BDㄷ平面 BDM，∴ 平面MBD⊥平面 PAD .(2)过点 P 作PO⊥AD，∵ 平面PAD⊥平面 ABCD，∴ PO⊥平面 ABCD，∴ PO 为四棱锥底面 ABCD 的高，又∵ △PAD 是边长为 4 的等边三角形，由 (1) 可知△ABD 是直角三角形，斜边 AB 上的高为：∴ 梯形的面积为：∴ 四棱锥 P-ABCD 的体积为：。

专题23 空间中的平行与垂直证明技巧一．【学习目标】（1）熟练掌握线面平行、面面平行的判定定理和性质，会把空间问题转化为平面问题．（2）学会应用“化归思想”进行“线线问题、线面问题、面面问题”的互相转化．（3）能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题．（4）熟练掌握空间中线面垂直的有关性质与判定定理；运用公理、定理证明或判定空间图形的垂直关系的简单命题．不论何种“垂直”都能化归到“线线垂直”二.【知识点及方法归纳】1．直线与平面平行的判定(1)判定定理：如果平面外一条直线和这个平面内的一条直线，那么这条直线和这个平面平行，即a∥b，a⊄α，b⊂α⇒a∥α.(2)如果两个平面平行，那么一个平面内的直线与另一个平面平行，则a∥β. 2．直线与平面平行的性质如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交；那么这条直线就和平面平行，即a∥α，a⊂β，α∩β＝b，．3．直线与平面垂直的判定(1)(定义)如果一条直线和平面内任意一条直线都垂直，那么这条直线和这个平面垂直．(2)(判定定理1)如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面．用符号语言表示为：若m⊂α，n⊂α，m∩n＝B，l⊥m，l ⊥n，则l⊥α.(3)如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面．用符号语言表示为：若a∥b，a⊥α，则b⊥α.(4)(面面垂直的性质定理)如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．(5)(两平面平行的性质定理)如果两个平面平行，那么与其中一个平面垂直的直线也与另一个平面垂直．(6)如果两个相交平面都垂直于第三个平面，那么它们的交线也垂直于第三个平面．4..两平面平行的判断方法(1)依定义采用反证法.(2)依判定定理通过说明一平面内有两相交直线与另一平面平行来判断两平面平行.(3)依据垂直于同一直线的两平面平行来判定.(4)依据平行于同一平面的两平面平行来判定.5.平行关系的转化程序线线平行线面平行面面平行从上易知三者之间可以进行任意转化，因此要判定某一平行的过程就是从一平行出发不断转化的过程.在解题时要把握这一点，灵活确定转化思路和方向.三【解题方法总结】1．证明直线与平面平行和直线与平面垂直常运用判定定理，即转化为线线的平行与垂直关系来证明．2．直线与平面平行的判定方法： (1)a ∩α＝∅⇒a ∥α(定义法)，(2)⎭⎪⎬⎪⎫a ∥b a ⊄αb ⊂α⇒a ∥α，这里α表示平面，a ，b 表示直线．【点睛】本题主要考查了平面的基本性质和空间中两直线的位置关系，其中解答中熟记平面的基本性质和空间中两直线的位置关系是解答的关键，着重考查了推理与论证能力，属于基础题。

用向量的数量积公式证明空间中的垂直问题利用向量的数量积公式为工具解决立体几何中的有关问题，可以有效克服单纯根据“形”进行推理的困难，从而降低学习立体几何的难度。

下面就空间中的垂直问题加以说明。

1、证明直线与直线垂直，可以转化为证明这两条直线上的非零向量的数量积为零。

反之易成立。

例1已知四面体ABCD 中，BD AC CD AB ⊥⊥,，求证：BC AD ⊥。

证明：因为BD AC CD AB ⊥⊥,，0,0=⋅=⋅∴BD AC CD AB ， )()(+⋅+=⋅ ⋅++⋅+⋅=2)(++⋅=0=⋅=， BC AD ⊥∴，BC AD ⊥∴。

2、证明直线与平面垂直，可以转化为证明这条直线上的非零向量与平面内两相交直线上的非零向量的数量积都为零。

例2已知平行六面体1111D C B A ABCD -的低面ABCD 是菱形，且CD C CB C 11∠=∠060=∠=BCD 。

（1）求证：BD C C ⊥1；（2）当1CC CD 值等于多少时，能使⊥C A 1平面BD C 1？（1）证明：设=a ，=b ，=1CC c ，则|a |=|b |，且<a,b >=<a,c >=<b,c >060=。

从而)(1CC -⋅=⋅=c •（a--b ）=|c ||a |cos <a,c >|-c||b|cos <b,c >0=，BD C C ⊥1,ABCD ADCB 1A1B1C1DBD C C ⊥∴1。

（2）解：设当)0(1>=x x CC CD时，能使⊥C A 1平面BD C 1。

此时，|a |=|b |=x |c |，不妨令|c |=1。

故=1CA a+b+c ，=D C 1a -c ，=a-b ， 于是由011=⋅C CA 得：0232=--x x ，解得：321-==x x 或(舍去)。

又01=⋅CA 恒成立，∴当111==CC CDx ，即时，⊥C A 1平面BD C 1。

空间向量的垂直判定空间向量是三维空间中的有向线段，它在数学和物理领域具有广泛的应用。

在解决空间向量问题时，常常需要确定两个向量是否垂直。

本文将介绍判定空间向量垂直的方法和应用。

一、向量的定义与表示向量是具有大小和方向的量，常用箭头表示。

在三维空间中，向量可以表示为：AB = (x1, y1, z1)，其中x1、y1、z1分别表示向量AB在x、y、z轴上的分量。

二、向量的垂直判定方法判定向量垂直有两种常见方法：内积法和向量积法。

1. 内积法两个向量垂直的充要条件是它们的内积等于0。

设向量A和向量B 分别为：A = (x1, y1, z1),B = (x2, y2, z2)，则向量A与向量B垂直的条件为：x1*x2 + y1*y2 + z1*z2 = 0。

2. 向量积法两个向量垂直的充要条件是它们的向量积等于零向量。

设向量A和向量B分别为：A = (x1, y1, z1),B = (x2, y2, z2)，则向量A与向量B垂直的条件为：(x1, y1, z1) × (x2, y2, z2) = (0, 0, 0)，即：y1*z2 - y2*z1 = 0,z1*x2 - z2*x1 = 0,x1*y2 - x2*y1 = 0。

三、向量垂直判定的应用1. 平面垂直判定在三维空间中，平面可以用向量方程表示，其法向量为向量n = (A, B, C)。

若向量n与已知直线的方向向量垂直，则该直线与平面垂直。

2. 直线垂直判定在三维空间中，直线也可以用向量方程表示，若两直线的方向向量垂直，则这两条直线互相垂直。

3. 圆锥曲线垂直判定对于椭圆、双曲线、抛物线等圆锥曲线，判定其切线与半焦弦的垂直性，可以利用向量的垂直判定方法。

四、示例分析以向量A = (1, 2, 3)和向量B = (2, -1, 1)为例，利用内积法和向量积法来判断两个向量是否垂直。

1. 内积法：向量A与向量B的内积为：1*2 + 2*(-1) + 3*1 = 2 + (-2) + 3 = 3，由于内积不等于0，所以向量A与向量B不垂直。