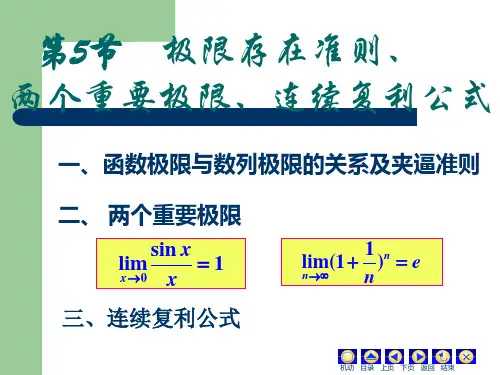
极限存在准则两个重要极限公式

极限存在准则两个重要极限公式首先，我们来介绍极限保号公式。

设函数f(x)在点a的一些邻域内有定义，如果存在常数M>0，使得对于任意的x∈(a-h,a+h)（h>0），都有，f(x)，≤M，则称M为f(x)在点a处的一个保号常数。

现在我们来证明极限保号公式：假设f(x)在其中一点a的一些邻域内有定义，并且存在常数M>0，使得对于任意的x∈(a-h,a+h)（h>0），都有，f(x)，≤M。

如果limx→af(x)=L存在，那么L也满足，L，≤M。

证明：由于limx→a f(x)=L存在，那么对于任意的ε>0，存在δ>0，使得对于任意的x∈(a-h,a+h)（h>0），如果0<，x-a，<δ，那么有，f(x)-L，<ε。

现在我们取ε=M，那么存在δ>0，使得对于任意的x∈(a-h,a+h)，如果0<，x-a，<δ，那么有，f(x)-L，<M。

这说明，对于任意的x∈(a-h,a+h)，如果0<，x-a，<δ，那么有，f(x)，=，f(x)-L+L，≤，f(x)-L，+，L，<M+，L。

我们再取任意的x∈(a-h,a+h)，如果0<，x-a，<δ，那么有，f(x)，≤M+，L，但是我们已经知道，在点a的一些邻域内存在保号常数M>0，使得对于任意的x∈(a-h,a+h)，都有，f(x)，≤M。

所以有，L，≤M。

这就是极限保号公式的证明。

接下来我们来介绍夹逼准则。

设函数f(x)、g(x)、h(x)在点a的一些邻域内有定义，并且对于任意的x∈(a-h,a+h)（h>0），都有g(x)≤f(x)≤h(x)。

如果limx→a g(x)=limx→a h(x)=L存在，那么limx→a f(x)=L也存在。

证明：对于任意的ε>0，由于limx→a g(x)=L存在，那么存在δ1>0，使得对于任意的x∈(a-h,a+h)，如果0<，x-a，<δ1，那么有，g(x)-L，<ε。

两个极限存在准则和两个重要的极限第一个极限存在准则是柯西-斯维亚切斯极限存在准则（Cauchy-Schwarz Limit Existence Criteria）。

其表述为：对于一个函数 f(x)，如果对于任意的ε>0，存在一个δ>0，使得当 0<，x-a，<δ 时，总有，f(x)-f(a)，<ε，则函数 f(x) 在点 a 处存在极限。

第二个极限存在准则是海涅定理（Heine's Theorem），也被称为局部有界性定理（Local Boundedness Theorem）。

其表述为：如果对于一个函数 f(x)，在点 a 的一些邻域内 f(x) 有界，即存在一个常数 M>0，使得对于所有的x∈(a-δ,a+δ) 有，f(x)，≤M，则函数 f(x) 在点 a 处存在极限。

这两个极限存在准则都用于判断函数在其中一点处的极限是否存在。

柯西-斯维亚切斯极限存在准则要求函数在该点的极限存在时，对于任意给定的ε>0，都能找到对应的δ>0，使得函数值与极限值的差小于ε。

而海涅定理则要求函数在该点附近有界，即函数在该点附近的函数值都不超过一些常数M。

这两个定理的应用范围和方法略有不同。

除了极限存在准则外，还有两个重要的极限：无穷小与无穷大。

无穷小是指极限趋近于零的数列或函数。

对于一个数列 {a_n}，如果对于任意的正数ε>0，存在正整数 N，使得当 n>N 时，有，a_n，<ε，则该数列是无穷小。

对于一个函数 f(x)，如果在其中一点 a 处，有lim(x→a) f(x)=0，则该函数在点 a 处是无穷小。

无穷大则是指极限趋于无穷的数列或函数。

对于一个数列 {a_n}，如果对于任意的正数 M>0，存在正整数 N，使得当 n>N 时，有，a_n，>M，则该数列是无穷大。

对于一个函数 f(x)，如果在其中一点 a 处，有lim(x→a) f(x)=∞（或表示为lim(x→a) ，f(x)，=∞），则该函数在点 a 处是无穷大。

两个重要极限公式
两个重要极限公式：极限是微积分中的基础概念，它指的是变量在一定的变化过程中，从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值（极限值）。

1、第一个重要极限的公式：
lim sinx / x = 1 (x->0)当x→0时，sin / x的极限等于1。

特别注意的是x→∞时，1 / x是无穷小，根据无穷小的性质得到的极限是0。

2、第二个重要极限的公式：
lim (1+1/x) ^x = e（x→∞）当x →∞时，（1+1/x）^x的极限等于e；或当x →0 时，(1+x）^（1/x）的极限等于e。

极限的求法
连续初等函数，在定义域范围内求极限，可以将该点直接代入得极限值，因为连续函数的极限值就等于在该点的函数值。

利用恒等变形消去零因子（针对于0/0型）
利用无穷大与无穷小的关系求极限。

利用无穷小的性质求极限。

利用等价无穷小替换求极限，可以将原式化简计算。

利用两个极限存在准则，求极限，有的题目也可以考虑用放大缩小，再用夹逼定理的方法求极限。

极限存在准则两个重要极限公式极限存在准则是数学中的一个重要概念，用于判断一个函数在其中一点处的极限是否存在。

在实际应用中，掌握极限存在准则对于求解极限问题非常重要。

在极限存在准则中，有两个非常重要的极限公式，分别是极限的保号性和夹逼定理。

首先，我们来介绍一下极限的保号性。

设函数f(x)在点x0的一些去心邻域内有定义，如果存在一个常数L，使得当x在x0的一些去心邻域内取值，并且f(x)>L，那么可以得出极限lim(x→x0)f(x)≥L；反之，如果存在一个常数L，使得当x在x0的一些去心邻域内取值，并且f(x)<L，那么可以得出极限lim(x→x0)f(x)≤L。

这就是极限的保号性。

保号性的一个重要应用是判断函数的极值。

如果在x0的一些去心邻域中，函数f(x)>0或f(x)<0，并且极限lim(x→x0)f(x)存在，那么就可以得出f(x)在x0处的极限是f(x0)。

这是因为根据保号性，当f(x)在x0的一些去心邻域内取正值时，可以推出极限lim(x→x0)f(x)≥0；同理，当f(x)在x0的一些去心邻域内取负值时，可以推出极限lim(x→x0)f(x)≤0。

由于极限存在，所以这时候只有一个可能，即极限lim(x→x0)f(x)等于0，即f(x)在x0处的极限是f(x0)。

下面我们来介绍夹逼定理。

设函数f(x)、g(x)和h(x)在其中一点x0的一些去心邻域内有定义，并且对于x在该邻域内取值，有f(x)≤g(x)≤h(x)。

如果极限lim(x→x0)f(x)和lim(x→x0)h(x)都存在，并且它们的极限值相等，即lim(x→x0)f(x)=lim(x→x0)h(x)=L，那么可以得出lim(x→x0)g(x)=L。

这就是夹逼定理。

夹逼定理常用于求极限的问题中，特别是当函数的表达式较复杂时，可以用一个更容易处理的函数夹逼该函数，从而求得极限。

夹逼定理的原理是通过限制函数g(x)在f(x)和h(x)之间，确定了极限的上下界。

极限存在准则两个重要极限公式一、夹逼定理夹逼定理是指在一些区间内，对于一个函数f(x)在其中一点x=c左右两侧或者趋近于x=c的时候，都存在一个函数g(x)和函数h(x)，并且有以下关系：f(x)≤g(x)≤h(x)，当x→c时，有g(x)→L，h(x)→L，则有f(x)→L。

夹逼定理的基本思想是找到两个函数，一个函数比所要研究的函数小，一个函数比所要研究的函数大，并且这两个函数的极限相等，则可以推导出所要研究的函数的极限存在，并且与这两个函数的极限相等。

夹逼定理的应用非常广泛，特别是在计算不定型极限、无穷小量极限时，往往可以利用夹逼定理来确定极限的存在与值。

例如，在计算sinx/x的极限的时候，我们可以认为0<x<π/2，因此有0<sinx<x<π/2，又因为sinx是一个有界函数，所以我们可以得到0≤sinx/x≤1，根据夹逼定理，当x趋近于0时，sinx/x极限存在并且为1二、洛必达法则洛必达法则是一种计算不定型极限的有效方法。

对于形如f(x)/g(x)型的不定型极限，其中f(x)和g(x)作为函数分别在其中一点x=c处连续，且f(c)=g(c)=0或者都是无穷小量的时候，可以用洛必达法则来求解极限。

具体求解方法如下：1.计算函数f(x)和g(x)的导数，即f'(x)和g'(x)。

2.当f'(x)/g'(x)在其中一点x=c处极限存在且不为0时，即存在f'(c)/g'(c)的时候，可以得到极限lim(x→c)(f(x)/g(x))=lim(x→c)(f'(x)/g'(x))=f'(c)/g'(c)。

洛必达法则的基本思想是通过两个函数的导数的极限来推导函数的极限。

利用洛必达法则，我们可以求解许多常见的不定型极限，比如0/0型、∞/∞型、0×∞型等。

例如，我们求解lim(x→0)(sinx/x)的极限，我们可以计算该极限的导数，f(x)=sinx, g(x)=x，导数分别为f'(x)=cosx, g'(x)=1，那么根据洛必达法则，我们可以得到该极限lim(x→0)(sinx/x)=lim(x→0)(cosx/1)=1总结：夹逼定理和洛必达法则是数学分析中两个非常重要的极限公式。

两个极限存在准则和两个重要的极限1.两个极限存在准则(1) 夹逼准则：设a, b, c为实数，如果函数f(x)在a的一些左邻域内对于一切x都有h(x)≤f(x)≤g(x)，且lim[x→a]h(x)=lim[x→a]g(x)=L，则必有lim[x→a]f(x)=L。

夹逼准则的本质是通过构造两个函数作为边界来确定原函数的极限。

(2) 单调有界准则：设函数f(x)在(a, b)上单调递增(递减)，且在(a, b)上有界，则必有lim[x→a]f(x)=sup{f(x)}(或lim[x→a]f(x)=inf{f(x)})。

单调有界准则的基本思想是通过函数的单调性和有界性来确定极限。

(1) 无穷小极限：设函数f(x)在x=a处有极限lim[x→a]f(x)=0，如果对于任意正数ε，存在对应的正数δ，使得对于所有满足0<，x-a，< δ的x，有，f(x)，<ε，那么称函数f(x)在x=a处的极限为0。

无穷小极限的重要性在于它在微积分中有广泛应用。

例如，微分定义中的导数可以看作是函数在其中一点的极限，这也符合函数在该点的变化趋势比较明显。

无穷小极限的概念使得我们能够更好地描述和理解函数在其中一点的变化情况。

(2) 无穷大极限：设函数f(x)在x=a处有极限lim[x→a]f(x)=∞，如果对于任意正数M，存在对应的正数δ，使得对于所有满足0<，x-a，< δ的x，有f(x) > M，那么称函数f(x)在x=a处的极限为无穷大。

无穷大极限的重要性在于它可以帮助我们研究函数在其中一点的增长速度和趋势。

例如，在极限定义中，我们可以通过无穷大极限来刻画函数在其中一点的无限增长或无限逼近的情况。

此外，无穷大极限也在微积分中的积分定义中有重要的应用，帮助我们理解函数的积分和面积的概念。

综上所述，极限的存在准则和重要的极限是微积分中的重要概念。

了解它们的定义和应用可以帮助我们更好地理解和分析函数在其中一点的变化情况，为进一步研究微积分和数学分析打下坚实的基础。