当前位置：文档之家 › 两个重要极限公式

两个重要极限公式

  • 格式：ppt
  • 大小：1.60 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

两个常用的极限公式

两个常用的极限公式

两个常用的极限公式
在数学中，极限是一种非常重要的概念，经常会用到极限公式来求极限。

在这里介绍两个常用的极限公式：
1. 夹逼定理：夹逼定理也叫夹逼准则，它是求极限的一种重要方法。

夹逼定理的基本思想是，如果一个函数在两个函数之间，而这两个函数的极限相等，那么这个函数的极限也等于它们的极限。

2. L'Hospital法则：L'Hospital法则又称洛必达法则，通常用于解决极限中的无穷小与无穷大的问题。

L'Hospital法则的基本思想是，对于一个不定式，如果它的分子和分母在某个点的极限都为0或都为无穷大，那么这个不定式的极限等于对分子和分母分别求导后再取极限。

这两个极限公式在数学中经常被用到，使用起来比较方便，但是在使用时也需要注意一些细节问题。

- 1 -。

几个重要极限公式

几个重要极限公式

几个重要极限公式
1. 欧拉公式：
欧拉公式是数学中的一项重要极限公式，由著名数学家欧拉提出，在数学中具有重要的应用价值。

具体来说，欧拉公式表示为:e^(iπ)+1=0
其中，e是自然对数的底数，i表示虚数单位，π表示圆周率。

2. 格朗沃尔定理：
格朗沃尔定理是微积分中的一项重要极限公式，由法国数学家格
朗沃尔提出。

格朗沃尔定理表示为∫_{a}^{b}f'(x)dx=f(b)-f(a)
其中，∫表示积分符号，f(x)表示被积函数，f'(x)表示其导数，
a和b为积分区间。

3. 斯特林公式：
斯特林公式是组合数学中的一项经典极限公式，由苏格兰数学家
斯特林提出并证明。

斯特林公式表示为:n!=sqrt(2πn)*(n/e)^n
其中，n！表示n的阶乘，e表示自然对数的底数，π表示圆周率。

这三个极限公式都是数学中的重要定理，广泛应用于各个领域。

欧拉公式与电工学有关，格朗沃尔定理与微积分有关，斯特林公式与组合数学和统计学有关。

掌握这些公式的应用方法不仅有助于我们深入了解数学的本质，也能够帮助我们更好地应用数学知识解决实际问题。

两个重要极限

两个重要极限
x 0 x 0
两边夹定理可知， lim | sin x | 0 , 从而 lim sin x 0.
图 2.13 例6.2 证明 lim cos x 1.
x 0
2 x x x 证 当 x 在 0 附近，即当 | x | 时, 由半角公式知 0 1 cos x 2 sin 2 2( )2 . 2 2 2 2
36
1 n 重要极限二： lim (1 ) e. n n 1 n 我们可以利用单调有界数列必有极限来证明 lim (1 ) 的存在性。 n n 1 n 证 设 f (n) (1 ) . 先证 f (n) 单调增加。事实上，由二项式展开有 n 1 n n 1 n( n 1) 1 n( n 1)(n 2) 1 f ( n) (1 ) 1 2 3 n 1! n 2! n 3! n n( n 1)(n 2)...(n n 1) 1 ﹢ n n! n 1 1 1 1 1 2 1 (1 ) (1 )(1 ) 1! 2! n 3! n n 1 1 2 n 1 (1 )(1 )(1 ). 同理有 n! n n n 1 n 1 1 1 1 1 2 1 f (n 1) (1 ) 1 (1 ) (1 )(1 ) n 1 1! 2! n 1 3! n 1 n 1 1 1 2 n 1 (1 )(1 )(1 ) n! n 1 n 1 n 1
n
例 6.13
求 lim
sin x . sin x sin(x) lim 2 2 x x ( x x)(x)
lim 例 6.14
2 2 sin( x) lim 1 . x x x x 2 2
例 6.8

极限存在准则两个重要极限

极限存在准则两个重要极限

sin x 即 cos x < < 1, x
π 上式对于 − < x < 0也成立. 2
当 0 < x < 时, 2
π
2 x x 2 x , = 2 sin 2 < 2( ) = 0 < cos x − 1 = 1 − cos x 2 2 2
x2 Q lim = 0, x →0 2
∴ lim cos x = 1,
x
+9
1 x x
)
= lim (9
x → +∞
x
1 x x
)
1 x + 1 3
0
1 x
3 1 = 9 ⋅ lim 1 + x x → +∞ 3

1 3x ⋅x
= 9⋅e = 9
∴ {xn } 是单调递增的 ;
1 1 1 1 xn < 1 + 1 + + L + < 1 + 1 + + L + n −1 2! n! 2 2 1 = 3 − n − 1 < 3, ∴ {xn } 是有界的 ; 2 1n ) ∴ lim x n 存在. 记为lim(1 + ) = e (e = 2.71828L n→∞ n→∞ n
x→0
∴ lim(1 − cos x ) = 0,
x→0
又 Q lim 1 = 1,
x→0
sin x sinx ∴lim = 1. x→0 x
注
此结论可推广到
sinϕ( x) lim =1 x→a ϕ( x)
条件是x → a时,ϕ( x) → 0，其中a可为 有限值， 有限值，也可为∞

极限存在准则两个重要极限公式

极限存在准则两个重要极限公式

x x0
(x )
(x )
lim f (x) A
x x0 (x )
准则I和准则I′统称为夹逼准则.
注意:利用夹逼准则求极限的关键:构造出 yn 与 zn ,
且 yn与zn的极限是易求的.
2020/6/15
2
例1 求 lim( 1 1 1 ).
n n2 1 n2 2
n2 n
解： 因为 n < 1 + L + 1 < n
单调下降有下界数列必有极限 说 明:
(1) 在收敛数列的性质中曾证明：收敛的数列一定
有界，但有界的数列不一定收敛．
(2) 利用准则I I来判定数列收敛必须同时满足 数列
单调和有界这两个条件．
2020/6/15
9
(3) 准则 I I只能判定数列极限的存在性，而未给出 求极限的方法．
例如，数列 xn (1)n ，虽然有界但不单调； 数列 xn n ，虽然是单调的，但其无界， 易知，这两数列均发散．
sin x
=
1
5
x® 0 x
例2 求
解:
lim
x0
tan x
x
lim x0
sin x
x
1 cos
x
lim
x0
sin x
x
lim 1 x0 cos
x
1
例3 求
解: 令 t arcsin x, 则 x sin t , 因此
原式 lim t t0 sin t
sin t 1
t
注: 利用变量代换，可得更一般的形式 lim sin (x) 1 (x)0 (x)
(4) 对于准则I I函，数极限根据自变量的不同变化过程 (x x0 , x x0 , x , x , x ) 也有类似的 准则， 只是准则形式上略有不同. 例如，

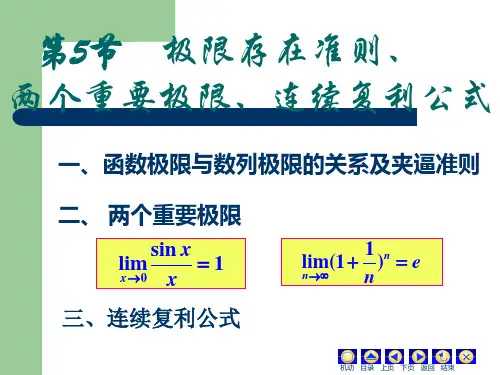
极限存在准则、两个重要极限和连续复利公式

极限存在准则、两个重要极限和连续复利公式

x x0 ( x )
x x0 ( x )
那末 lim f ( x)存在, 且等于A. x x0 ( x)
准则 I和准则 I'称为夹逼准则.
注 利用夹逼准则求极限关键是构造出 yn与zn ,
并且 yn与zn的极限是容易求的 .
例1 求 lim( 1 1 1 ).
n n2 1 n2 2
n2 n
又 x1 3 3, 假定 xk 3, xk1 3 xk 3 3 3,
xn是有界的;
lim n
xn
存在.
xn1
3 xn ,
x2 n1
3
xn ,
lim
n
x
2 n
1
lim(3
n
xn ),
A2 3 A, 解得 A 1 13 , A 1 13 (舍去)
2
2
1 13
lim n
t t 1
t 1
lim(1 1 )x e
x
x
令t 1, x
lim(1
1
x)x
lim(1
1)t
e.
x0
t
t
1
lim(1 x) x e
x0
三、连续复利
设本金为 A0 ，年利率为 r ，则
一年末的本利和 A1 A（0 1 r)
二年末的本利和 A2 A（1 1 r) A0 (1 r)2
当 n N时, 恒有 a yn xn zn a ,
即 xn a 成立,
lim n
xn
a.
上述数列极限存在的准则可以推广到函数的极限
准则Ⅰ′
如果当
x
U
0
(
x 0
)
(或

两条极限重要公式

两条极限重要公式

两条极限重要公式好的，以下是为您生成的文章：在我们的学习生涯中，数学就像是一座神秘而又充满挑战的大山，而在这座大山中，有两条极限重要的公式，如同闪闪发光的宝石，指引着我们前进的方向。

还记得我上高中的时候，有一次数学考试，最后一道大题就是关于这两条公式的应用。

当时我看着题目，心里那叫一个紧张啊！题目是这样的：已知函数 f(x) = (x^2 - 1) / (x - 1)，当 x 趋近于 1 时，求函数的极限。

我心里想，这不就是要用那两条重要公式嘛！咱们先来说说这第一条重要公式，那就是“当x 趋近于某个值a 时，(x^n - a^n) / (x - a) 的极限等于 n * a^(n - 1)”。

就拿刚刚那道题来说，把函数 f(x) 化简一下，f(x) = (x + 1)(x - 1) / (x - 1) = x + 1 。

当 x 趋近于 1 时，极限就是 2 。

是不是很神奇？再来说说第二条公式，“当 x 趋近于无穷大时，(1 + 1/x)^x 的极限等于 e （约等于 2.718）”。

这公式可厉害了，在很多实际问题中都能派上大用场。

就像有一次，我在研究一个经济增长模型，里面就用到了这个公式。

假设一个企业每年的增长率是 10%，如果持续增长下去，经过很长时间后，它的规模增长就可以用这个公式来近似计算。

这两条公式，在我们解决各种数学问题的时候，那可真是“大功臣”。

无论是在计算函数的极限、推导复杂的数学定理，还是在实际生活中的各种应用，它们都发挥着不可或缺的作用。

比如说，在工程领域，计算材料的强度极限；在物理学中，研究物体的运动速度极限；在金融学里，预测投资的长期收益极限。

可以说，这两条公式就像是一把万能钥匙，能打开很多知识的大门。

然而，要真正掌握这两条公式，可不是一件轻松的事儿。

需要我们不断地练习、思考和总结。

有时候，做一道题可能会花费很长时间，还会出错，让人感到沮丧。

但只要坚持下去，突然有一天，就会发现自己能熟练运用了，那种成就感真是无与伦比。

极限存在准则两个重要极限公式

极限存在准则两个重要极限公式

夹逼准则不仅说明了极限存在，而且给出了求极限的
方法．下面利用它证明另一个重要的
极限公式： lim sin x 1 x0 x
证:
当
x
(
0
,
2
)
时，
BD
1x
oC
A
△AOB 的面积＜圆扇形AOB的面积＜△AOD的面积
即
1 2
sin
x
1 2
x
1 2
tan
x
亦故即有
1sin sxinxxxctoa1snxx
1. 单调有界准则
数列 xn : 单调增加 x1 x2 xn xn1 ,
单调减少 x1 x2 xn xn1 ,
准则I 单调有界数列必有极限 单调上升有上界数列必有极限
说 明: 单调下降有下界数列必有极限 (1) 在收敛数列的性质中曾证明：收敛的数列一定 有界，但有界的数列不一定收敛．
1
1 1 n1 n 1
1 yn1
由于数列 yn 是单调增加的，所以数列 zn 是单调减少的.
又
xn
1
1
n
n
1
1
ห้องสมุดไป่ตู้n1
n
zn
z1
4
则 2 xn 4. 综上，根据极限存在准则Ⅰ可知，数列是
收敛的.
2023年12月9日星期六
4
目录
上页
下页
返回
通常用字母 e 来表示这个极限，即
lim
n
1
1
n
)
( n 1, 2,
), 且
x1 0,
a0,
求
lim
n
xn
.
利用极限存在准则

极限存在准则与两个重要极限

极限存在准则与两个重要极限

100 000 2.718 27 100 000 2.718 30
1 000 000 2.718 28 1 000 000 2.718 28
e e
1.2 准则Ⅱ与第二个重要极限
因此，
lim
x
1
1 x
x
e
．
e 是无理数，它的值是 2.718 28 ．在 1.1 中提到的指数函数 y ex 及自然对数 y ln x 中的
（2） lim g(x) lim h(x) A ，
xx0
xx0
则有 lim f (x) A ． xx0
1.1 准则Ⅰ与第一个重要极限
作为准则Ⅰ及准则Ⅰ'的应用，下面证明一个重要极限： lim sin x 1 ． x0 x
证明 在图所示的单位圆中，设圆心角 BOA x ， AD 切圆 O 于 A ， 且与 OB 延长线相交于 D ，于是有
3 1
x 1
1
lim
x 1
3
x
2x 1
2x
lim
x
2x 2x
3 1
lim
x
1 1
3
x
2x
1 x 2x
1
3
e2
1
e2
e．
1.7 无穷小阶的比较
在 1.4 节中我们已经知道，两个无穷小的和、差及乘积仍是无穷小．但是关于两
个无穷小的商却会出现不同的情况．例如，当 x 0 时，2x ， x2 ，sin x 都是无穷小
an1
1
n
1
n1
1
1
1
21!1
n
1
1
1 3!
1
1 n
1

极限存在准则两个重要极限公式

极限存在准则两个重要极限公式

令t =1x, 则:
lim(1
1
x)x
=
lim(1
1)t
=
e.
x0
t
t
此结论可推广到
1
lim1 ( x)( x) = e
xa
条件是x a时, ( x) 0，其中a可为
有限值，也可为
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
14
例5 求 lim(1 1 )x .
n2 n n2 1
又 lim n
n = lim n2 n n
1 1 1 = 1,
n
lim
n
n = lim n2 1 n
1 = 1,
1 1 n2
由夹逼定理得
lim( 1 1 L 1 ) = 1.
n n2 1 n2 2
n2 n
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
6
例2 证明数列 xn = 3 3 L 3 (n重根 式)的极限存在.
证: 显然 xn1 > xn , xn是单调递增的 ;
又 x1 = 3 3, 假定 xk 3, xk1 = 3 xk 3 3 3,
xn 是有界的 ;
原式
=
lim x (1
x 1 )x
x
=
e e 1
=
e2
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
16
三、小结
1.两个准则
夹逼准则; 单调有界准则 .
2.两个重要极限
10 lim sin x = 1; x0 x

两个重要极限及其应用

两个重要极限及其应用

两个重要极限及其应用作者：刘凤艳来源：《科技资讯》2011年第31期摘要：本文讨论两个重要极限及它们的应用，使学生快速找到解决此类求极限问题的方法。

关键词：重要极限应用方法中图分类号:G4 文献标识码:A 文章编号:1672-3791(2011)11(a)-0189-01《高等数学》微积分学中有两个重要极限公式，这两个重要极限的变形，在求解极限问题时也有一些重要应用。

1 第一个重要极限的推广式其中是连续的函数。

也就是说首先分子分母的比值是型，其次正弦后面的表达式和分母的表达式是相同的，这时就可以应用重要极限的推广式。

例1:求。

解：例2:求。

解：例3:求。

解：从以上三例题可以看出，只要是，都有，而又分为这三种情况。

2 第二个重要极限的两种推广形式(1)例4:求。

解：例5:求。

解：例6:解：从这几道例题可以看出，只要满足推广形式1即可应用第二个重要极限。

而又有三种情况：(2)例7:求解：故也可利用以下结论：，，则只要满足推广形式2即可应用第二个重要极限。

而又有三种情况：。

无论是哪个重要极限，无论是或者是，都不是单指一个数的变化趋势，而是一个式子或者是一个函数的变化趋势。

参考文献[1] 同济大学数学系.高等数学(上册)[M].北京:高等教育出版社,2007:50.[2] 张喜堂.两个重要极限,函数的连续性[J].数学通讯，2001:38～39.[3] 郭爱主.谈两个重要极限的应用[J].湖南民族职业学院学报.2010:82～84.。

用两个重要极限 导数公式推导

用两个重要极限 导数公式推导

用两个重要极限导数公式推导导数是微积分中的重要概念，用于描述函数在某点处的变化率。

在求导过程中，有两个重要的极限公式被广泛应用，它们分别是极限的定义和导数的定义。

首先，我们来看极限的定义。

极限的定义表达了当自变量趋近于某个值时，函数取值的趋势。

具体而言，若对于任意给定的正数ε，存在与自变量a的距离δ，使得当x满足| x - a| < δ时，函数f(x)与L之差的绝对值小于ε，即| f(x) - L| < ε，那么我们称函数f(x)在x趋近于a时的极限为L。

其次，我们来探讨导数的定义。

导数定义了一个函数在某个点处的变化率，也就是斜率。

具体而言，对于函数y = f(x)，如果存在极限lim(x -> a) [f(x) - f(a)] / (x - a)，则称函数f(x)在点a可导，记作f'(a)。

这个极限值就是那个点a的导数，表示函数在这个点处的变化率。

通过极限的定义和导数的定义，我们可以求出函数在某点处的变化率。

具体而言，如果一个函数在某一点x0处可导，则在该点处的导数等于函数在该点处的切线的斜率。

计算公式为y = f(x0) +f'(x0)(x - x0)。

在数学和物理等领域中，导数的概念被广泛应用。

例如，在计算机科学中，我们可以使用导数来确定算法运行时间的复杂度。

在自然科学领域中，我们可以使用导数来计算物质在空间中的速度和加速度。

总之，通过极限的定义和导数的定义，我们可以求出函数在某点处的变化率，这是微积分中一个非常重要的概念。

理解这两个极限公式的应用，可以帮助我们更好地掌握微积分的知识，以此应用于各种实际问题中。

极限存在准则、两个重要极限和连续复利公式

极限存在准则、两个重要极限和连续复利公式

即 a yn a , a zn a ,
当 n N时, 恒有 a yn xn zn a ,
即 xn a 成立,
lim n
xn

a.
上述数列极限存在的准则可以推广到函数的极限
准则Ⅰ′
如果当
x

U
0
(
x 2
)2

1 2

12
2
2
1. 2
2. lim(1 1 )n e
n
n
定义 lim(1 1)n e
n
n
设
xn

(1

1)n n
1 n 1 n(n 1) 1 n(n 1)(n n 1) 1
1! n 2! n2
n!
nn
1 1 1 (1 1) 1 (1 1)(1 2)(1 n 1).
C
B
1. lim sin x 1 x0 x
o
x
D
A
设单位圆 O, 圆心角AOB x, (0 x )
2
作单位圆的切线，得ACO .
扇形OAB的圆心角为 x , OAB的高为 BD ,
于是有 sin x BD, x 弧 AB, tan x AC ,
△AOB 的面积＜圆扇形AOB的面积＜△AOC的面积
sin x x tan x, 即 cos x sin x 1, x
上式对于 x 0也成立. 当 0 x 时,
2
2
注
lim cos x 1, 又lim1 1,
lim sin x 1.

1.6两个重要极限

1.6两个重要极限

定义: 设, 是同一过程中的两个无 穷小, 且 0.
(1) 如果 lim 0, 就说 是比高阶的无穷小 , 记作 o( ); ( 2) 如果 lim C (C 0), 就说 与是同阶的无穷小 ; 特殊地 如果 lim 1, 则称 与是等价的无穷小 ; 记作 ~ ;
1 x
1 令t x
因此
lim(1 x ) e
x0
1 x
1 x lim (1 ) e lim ( 1 x ) e x x0 x ; 该极限的特点: (1) 1 型未定式
(2) 括号中1后的变量(包括符号)与幂互为倒数.
1 型, 但第二个特点不具备, 则 若极限呈 注 通常凑指数幂使(2) 成立.
sin ( x ) 一般有 lim 1 ( x ) ( x) 0
sin 2 x sin 2x 2 例 lim lim x 0 x 0 x 2x sin kx sin kx k lim lim x0 x 0 x kx
1 2=2
1 k=k
3
sin ( x ) lim 1 ( x ) 0 ( x ) sin x 1 tan x 例 lim lim x0 x cos x x0 x sin x 1 lim lim 1 1 1 x 0 x x 0 cos x
rt
③
A0 At e rt
例题分析：
例1、用分期付款方式购买20万元一辆的轿车。设贷款期 限为5年，年率为4%。试计算5年末还款的本利和： 1）按离散情况计算，每年计息4次； 2）按连续复利计算。
r nt 解：１） 用复利公式At =A0 (1 ) n 由已知得 A0＝20， n = 4,r=0.04,t 5 0.04 45 A5 =20(1 ) 20 1.220995 24.4199(万元) 4 2） 用复利公式 At =A0 e rt
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
2 x x 2 x 2sin sin sin 1 1 2 1 2 1 2 2 解: 原式 lim lim lim 1 2 2 x 0 x 0 x 2 2 x 0 x 2 x 2 2 2
15
2016/3/2
内容小结
n
1 1 y 1 的极限都存在且都等于e ，即 lim 1 e x x x
利用变量代换，可得更一般的形式
1 ( x)
x
x
（x ) 0
2016/3/2
lim 1 ( x)
e
6
1 例1 求 lim 1 . x x
n 1 1 类似于 xn 1 单调性的证明可证得数列 yn 1 n n n 1
1 n 1 所以数列 z n 是单调减少的. 由于数列 yn 是单调增加的， n 1
1 1 又 xn 1 1 n n
单调减少 x1 x2 xn xn1 ,
准则I 单调有界数列必有极限 单调上升有上界数列必有极限 单调下降有下界数列必有极限 说 明: (1) 在收敛数列的性质中曾证明：收敛的数列一定 有界，但有界的数列不一定收敛． (2) 利用准则Ⅰ来判定数列收敛必须同时满足 数列 单调和有界这两个条件． 2016/3/2 2
令 N max N1 , N 2 , 则当 n N 时, 有
a y n xn z n a 即 xn a , 故 lim xn a . 2016/3/2
由条件 (1)
n
8
我们可将准则II推广到函数的情形： 准则II′
当 x ( x0 , ) 时, g ( x) f ( x) h( x) , 且 ( x X 0)
n n 1
zn z1 4
则 2 xn 4 . 综上，根据极限存在准则Ⅰ可知，数列是 2016/3/2 5 收敛的 .
通常用字母 e 来表示这个极限，即
1 lim 1 e (e 2.71828) n n
也可以证明，当 x 取实数而趋于 或 时，函数

1 1 1 （1）当 x 0 时， x( 1) x x , x x x
1 x 1. 同样有 xlim 0 x 2016/3/2
19
1 a 4. 设 xn 1 ( xn ) ( n 1 , 2 , ) , 且 x1 0 , 2 xn a 0 , 求 lim xn . 利用极限存在准则 n 1 a a xn 解： xn 1 (xn ) a 2 xn xn 1 a xn 1 1 a (1 2 ) ( 1 ) 1 2 a xn 2 xn
x x0

lim g ( x) lim h( x) A
x x0 ( x )
( x )
x x0 ( x )
lim f ( x) A
准则II和准则II′统称为夹逼准则. 注意: 利用夹逼准则求极限关键是构造出 yn 与 z n ,
并且 yn 与 z n的极限是容易求的 .
sin ( x) 注: 利用变量代换，可得更一般的形式 lim 1 ( x ) 0 ( x )
2016/3/2 14
t
例6 求
sin 3x 3 sin 3x 5 x lim 解: lim x 0 sin 5 x 5 x 0 3x sin 5 x 3 sin 3x 5x 3 lim lim 5 x 0 3x x 0 sin 5 x 5 1 cos x . 例7 求 lim 2 x 0 x
2016/3/2 9
例3 求 lim(
n
1 n2 1

1 n2 2

1 n2 n
).
n 1 1 n , 解： 2 2 2 2 n n n 1 n n n 1
n 又 lim 2 lim n n n n
lim n n 1
2
1 1 1 n
1 x 1 tan x 即 2 2 x 1 ) 1 sin x x tan x ( 0 x 故有 亦即 2 sin x cos x sin x ) 显然有 cos x 1 (0 x 2 x sin x 注 lim 1 lim cos x 1, x 0 x x 0 2016/3/2
2016/3/2
17
2. 求
2016/3/2
10 x 5 10 解： 原式 = lim lim 1 x x 5 x x5 x 5 10 5 10 10 lim 1 x x 5 x 5 10 5 10 10 10 lim 1 1 x x 5 x 5 x 5 10 5 10 10 10 10 lim 1 lim 1 e x x 5 x x 5
1. 极限存在的两个准则 夹逼准则; 单调有界准则 . 2. 两个重要极限
或 注:
2016/3/2
代表相同的表达式
16
思考与练习
1. 填空题 ( 1～4 ) sin x 0 ; 1. lim _____ x x 1 0 ; 3. lim x sin ____ x 0 x
1 1 ; 2. lim x sin ____ x x 1 1 n e 4. lim(1 )要极限：
1 首先，证 xn 1 是单调的． n n n n 1 1 1 1 1 1 xn 1 ＝ 1 1 1 1 1 1 1 1 1 1 n n n n n n
x
x
18
3. 证明 证明： 对任一 x R ，有 x 1 x x ，则当 x 0 1 1 1 时，有 1 . 于是, x x x
由夹逼准则得 lim x x 1 x 0 1 1 1 （2）当 x 0 时， x x x( 1), x x x 1
(3) 准则Ⅰ只能判定数列极限的存在性， 而未给出 求极限的方法．
n x ( 1) ，虽然有界但不单调； 例如，数列 n
数列 xn n ，虽然是单调的，但其无界，
易知，这两数列均发散． (4) 对于准则I， 函数极限根据自变量的不同变化过程 ( x x0 , x x0 , x , x , x ) 也有类似的 准则， 只是准则形式上略有不同. 例如， 准则I′ 设函数 f ( x) 在点 x0 的某个左邻域内单调 并且有界，则 f ( x) 在 x0 的左极限 f ( x0 ) 必存在． 2016/3/2
n 1
1 lim 1 ? n n
n
n
4
1 其次，证 xn 1 有界． 显然， xn x1 2 nn
n
1 z 是单调增加的．设数列 n 1 ，则 n n 1 n 1 1 1 1 1 n 1 zn 1 n 1 n 1 yn 1 1 n n n
x 3
x
2 e .
2
解:
x x lim 1 lim 1 x 0 x 0 3 3
1 x
3 1 x 3
3 x x lim 1 x 0 3
∴数列单调递减有下界， 设 lim xn A 故极限存在， n 1 a A a 则由递推公式有 A ( A ) 2 A x1 0 , xn 0 , 故 lim xn a
解:
1 原式 lim 1 x x
1 x
2x
x( 2)
x x 1 lim 1 例2 求 lim x 0 x 0 3 3
1 lim 1 x x 3 1
2016/3/2
1
11
sin x 极限公式： lim 1 x 0 x
证: 当 x ( 0 , ) 时， 2
1 sin x 2
夹逼准则不仅说明了极限存在，而且给出了求极限的 下面利用它证明另一个重要的 BD 方法．
1 x A o C
△AOB 的面积＜ 圆扇形AOB的面积＜△AOD的面积
第一章
第六节 极限存在准则 两个重要极限
（Existence criteria for limits & Two important limits）
一、极限存在的两个准则
二、两个重要极限
三、内容小结
2016/3/2 1
1. 单调有界准则
数列
xn : 单调增加 x1 x2 xn xn1 ,
12
例4 求
tan x sin x 1 sin x 1 解: lim lim lim lim 1 x 0 x x 0 x cos x x 0 x x 0 cos x
例5 求 解: 令 t arcsin x , 则 x sin t , 因此 t 原式 lim 1 sin t t 0 sin t
2 1 1 1 n2 n 2 2 n 2 2 2 n n n n n n n 2 2 1 n lim 1 lim 2 且 n 1 n n n n
1 n2 lim 1 lim 2 n 1 2 n n n 1 1 1 lim n 2 2 2 n n n 2 n n
1,
1 1 2 n 1 1 1 lim( 2 ) 1. 2 2 n n 1 n 2 n n