九年级(下)第六章 二次函数：第7课时 二次函数与一元二次方程

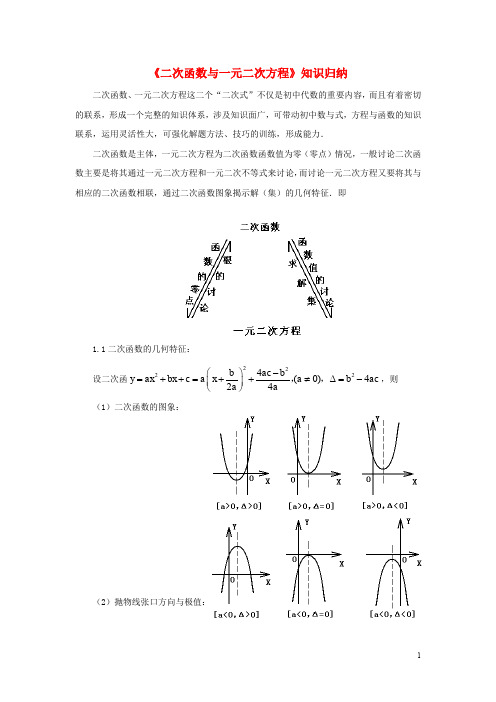
《二次函数与一元二次方程》知识归纳二次函数、一元二次方程这二个“二次式”不仅是初中代数的重要内容，而且有着密切的联系，形成一个完整的知识体系，涉及知识面广，可带动初中数与式，方程与函数的知识联系，运用灵活性大，可强化解题方法、技巧的训练，形成能力．二次函数是主体，一元二次方程为二次函数函数值为零（零点）情况，一般讨论二次函数主要是将其通过一元二次方程和一元二次不等式来讨论，而讨论一元二次方程又要将其与相应的二次函数相联，通过二次函数图象揭示解（集）的几何特征．即1.1二次函数的几何特征：设二次函22224(0)424b ac by ax bx c a x a b aca a-⎛⎫=++=++≠∆=-⎪⎝⎭，，，则（1）二次函数的图象：（2）抛物线张口方向与极值：张口向上，有极小值，244ac b y a -=；张口向下，有极大值，244ac b y a-=；（3）对称轴：2b x a=-． 对称轴在原点左侧a b ⇔，同号；对称轴在原点右侧a b ⇔，异号；对称轴与y 轴重合0b ⇔=．（4）顶点2424b ac b M a a ⎛⎫-- ⎪⎝⎭，．M 在x 轴上方a ⇔∆，异号；在轴下方a ⇔∆，同号；M 在x 轴上0⇔∆=，M 在直线y kx t =+上2424kb ac b t a a-⇔+=． （5）图象过点()m n ，，图象过点2()m n am bm c n ⇔++=，， 特别地：0m c n =⇔=（为截距）；00m n c ==⇔=；100m n a b c =±=⇔±+=，．1.2、二次函数与一元二次方程：函数2(0)y ax bx c a =++≠，当0y =时，即为一元二次方程20ax bx c ++=，故一元二次方程的解又叫二次函数的零点．令方程0y =的根为12x x ，，则有：二次函数的零点⇔抛物线与x 轴的交点⇔方程0y =的根．（1）交点个数：有两个交点12(0)(0)x x ⇔，，，方程0y =有不等实根0⇔∆>； 有一个交点1(0)x ⇔，方程0y =有等实根0⇔∆=； 无交点⇔方程0y =无实根0⇔∆<． （2）交点位置：两交点在原点两侧⇔方程0y =有异号根0ac ∆>⎧⇔⎨<⎩；两交点在原点同侧⇔方程0y =有同号根0ac ∆>⎧⇔⎨>⎩；两交点在原点右侧⇔方程0y =有两正根000ac ab ∆>⎧⎪⇔>⎨⎪<⎩；两交点在原点左侧⇔方程0y =有两负根000ac ab ∆>⎧⎪⇔>⎨⎪>⎩；两交点在两数αβ，之间或之外22()()0a b c a b c ααββ⇔++++>⇔方程1200()()0y x x αβ∆>⎧=⎨--<⎩；两交点一个在在两数αβ，之间22()()0a b c a b c ααββ⇔++++>⇔方程121200()()0()()y x x x x ααββ∆>⎧⎪=--⎨<⎪--⎩；两交点在数α的两侧2()0a a b c αα⇔++<⇔方程120()()0y x x αα∆>⎧=⎨--<⎩；两交点在数α的同侧2()0a a b c αα⇔++>⇔方程1200()()0y x x αα∆>⎧=⎨-->⎩；（3）两交点间距离12(0)d x x a⇔=-=∆≥． 例1已知二次函数2(0)y ax bx c a =++≠的图象如图所示： （1）试判断a b c ，，及24b ac -的符号； （2）若|OA |＝|OB |，试证明．分析：解本题主要是应用抛物线的几何特性（张口方向，对称轴，截距，与x 轴交点个数）及函数零点（方程）的有关知识，即（1）由抛物线张口方向、对称轴位置、截距及与x 轴交点个数，立即可得：0a >，20040b c b ac <<->，，．（2）由方程202A A b x OA x ax bx c a OB c OA OB ⎧⎫--=⇒=⎪⎪++=⇔⇔⎨⎬⎪⎪=-=⎩⎭，结论．例2已知二次函数244y x x m =++的图象与x 轴两交点和对称轴的交点构成一个正三角形的三个顶点，求函数解析式．分析：求解析式，即求m ，主要是应用抛物线的顶点、对称轴与轴的交点（即解方程）和三角形的有关知识，即：由方程212121440(10)2x x m x m x x -±++=⇒-⇒-=，≥由抛物线顶点0A ⎫⎪⎪⎝⎭，由两点间距离公式求出0A ⎫⎪⎪⎝⎭和0A ⎫⎪⎪⎝⎭的距离： 1214AC x x m =-⇒=（1m =舍去）． 例3m 为何值时，关于x 的方程28(1)(7)0x m x m --+-=的两根： （1）为正数根；（2）为异号根且负根绝对值大于正根； （3）都大于1；（4）一根大于2，一根小于2； （5）两根在0，2之间．分析：关于方程根的讨论，结合二次函数图象与x 轴的交点位置的充要条件即可求：即设方程两根为12x x ，则（1）12120079250x x m m x x ∆⎧⎪+>⇒<⎨⎪>⎩或≥≤≥；（2）12120010x x m x x ∆>⎧⎪+<⇒<⎨⎪<⎩；（3）12120225(1)(2)0x x m x x ∆⎧⎪+>⇒⎨⎪-->⎩≥≥； （4）12027(2)(2)0m x x ∆>⎧⇒>⎨--<⎩；（5）121212007925270(2)(2)0x x m m x x x x ∆⎧⎪+>⎪⇒<<⎨>⎪⎪-->⎩或≥≤≤．例4证明关于的不等式2(32)210k x kx k -++-<与2211012k x kx ⎛⎫-++> ⎪⎝⎭，当k 为任意实数时，至少有一个恒成立．分析：证明不等式恒成立，实质是证明对应抛物线恒在轴的上方或下方的问题，故只要求抛物线恒在轴上方或下方的充要条件即可．即由2(32)210k x kx k -++-<恒成立⇔对应抛物线恒在轴下方23201244(32)(1)0k k k k k -<⎧⇔⇒<⎨---<⎩；由2211012k x kx ⎛⎫-++> ⎪⎝⎭恒成立⇔对应抛物线恒在轴上方 2221012111334012k k k k k ⎧->⎪⎪⇔⇒<->⎨⎛⎫⎪--< ⎪⎪⎝⎭⎩或．因此，当k 为任意实教时，上述两充要条件至少有一个成立，命题得证．例5已知关于x 的方程222460x mx m -+-=两根为αβ，，试求22(1)(1)αβ-+-的极值．分析：求22(1)(1)αβ-+-的极值，即应用方程根与系数的关系和判别式，求二次函数的条件极值的问题．即αβ，为方程的两根20246m m m αβαβ⎧∆>⎪⇒+=⇒⎨⎪=-⎩22221(1)(1)()2()22152n u m αβαβαβαβ⎛⎫=-+-=+-+-+⇒=-++ ⎪⎝⎭，又max min 156m u u ⇒==-，。

二次函数与一元二次方程教案设计
教学目标
（一）教学知识点
1、能够利用二次函数的图象求一元二次方程的近似根。

2、进一步发展估算能力。

（二）能力训练要求
1、经历用图象法求一元二次方程的近似根的过程，获得用图象法求方程近似根的体验。

2、利用图象法求一元二次方程的近似根，重要的是让学生懂得这种求解方程的思路，体验数形结合思想。

（三）情感与价值观要求
通过利用二次函数的图象估计一元二次方程的根，进一步掌握二次函数图象与x轴的交点坐标和一元二次方程的根的关系，提高估算能力。

教学重点
1、经历探索二次函数与一元二次方程的关系的过程，体会方程与函数之间的联系。

2、能够利用二次函数的图象求一元二次方程的近似根。

教学难点
利用二次函数的图象求一元二次方程的近似根。

教学方法
学生合作交流学习法。

教具准备
投影片三张
第一张：（记作2。

8。

2a）
第二张：（记作2。

8。

2b）
第三张：（记作2。

8。

2c）
教学过程
Ⅰ、创设问题情境，引入新课
[师]上节课我们学习了二次函数y=ax2+bx+c（a0）的图象与x轴的交点坐标和一元二次方程ax2+bx+c=0（a0）的根的关系，懂得了二次函数图象与x轴交点的横坐标，就是y=0时的一元二次方程的根，于是，我们在不解方程的情况下，只要知道二次函数与x轴交点的横坐标即可。

但是在图象上我们很难准确地求出方程的解，所以要进行估算。

本节课我们将学习利用二次函数的图象估计一元二次方程的根。

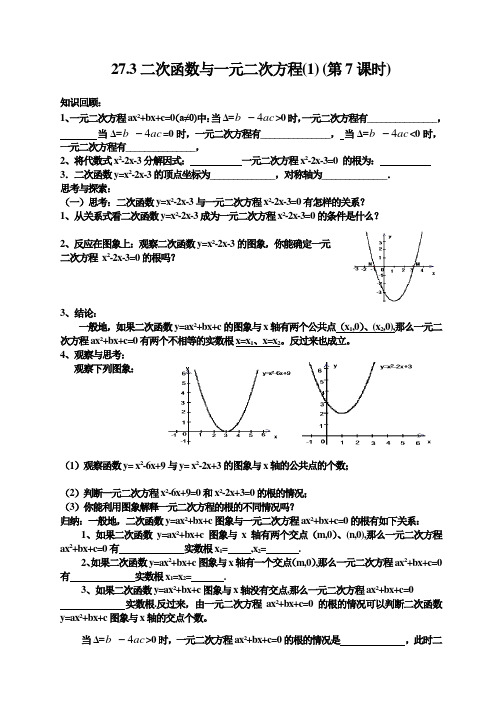
27.3二次函数与一元二次方程(1) (第7课时)知识回顾：1、一元二次方程ax2+bx+c=0（a≠0)中：当Δ=ac->0时，一元二次方程有_______________，b4当Δ=acb4-<0时，b4-=0时，一元二次方程有_______________，当Δ=ac一元二次方程有_______________，2、将代数式x2-2x-3分解因式：一元二次方程x2-2x-3=0 的根为：3．二次函数y=x2-2x-3的顶点坐标为______________，对称轴为______________．思考与探索：（一）思考：二次函数y=x2-2x-3与一元二次方程x2-2x-3=0有怎样的关系？1、从关系式看二次函数y=x2-2x-3成为一元二次方程x2-2x-3=0的条件是什么？2、反应在图象上：观察二次函数y=x2-2x-3的图象，你能确定一元二次方程x2-2x-3=0的根吗？3、结论：一般地，如果二次函数y=ax2+b x+c的图象与x轴有两个公共点（x1,0）、(x2,0),那么一元二次方程ax2+b x+c=0有两个不相等的实数根x=x1、x=x2。

反过来也成立。

4、观察与思考：观察下列图象：（1）观察函数y= x2-6x+9与y= x2-2x+3的图象与x轴的公共点的个数；（2）判断一元二次方程x2-6x+9=0和x2-2x+3=0的根的情况；（3）你能利用图象解释一元二次方程的根的不同情况吗？归纳：一般地，二次函数y=ax2+bx+c图象与一元二次方程ax2+b x+c=0的根有如下关系：1、如果二次函数y=ax2+b x+c图象与x轴有两个交点（m,0）、(n,0),那么一元二次方程ax2+bx+c=0有实数根x1= ,x2= .2、如果二次函数y=ax2+b x+c图象与x轴有一个交点（m,0）,那么一元二次方程ax2+bx+c=0有实数根x1=x2= .3、如果二次函数y=ax2+bx+c图象与x轴没有交点,那么一元二次方程ax2+bx+c=0实数根.反过来，由一元二次方程ax2+b x+c=0的根的情况可以判断二次函数y=ax2+b x+c图象与x轴的交点个数。

函数概念说课稿函数概念说课稿1一、说课内容：苏教版九年级数学下册第六章第一节的二次函数的概念及相关习题二、教材分析：1、教材的地位和作用这节课是在学生已经学习了一次函数、正比例函数、反比例函数的基础上，来学习二次函数的概念。

二次函数是初中阶段研究的最后一个具体的函数，也是最重要的，在历年来的中考题中占有较大比例。

同时，二次函数和以前学过的一元二次方程、一元二次不等式有着密切的联系。

进一步学习二次函数将为它们的解法提供新的方法和途径，并使学生更为深刻的理解“数形结合”的重要思想。

而本节课的二次函数的概念是学习二次函数的基础，是为后来学习二次函数的图象做铺垫。

所以这节课在整个教材中具有承上启下的重要作用。

2、教学目标和要求：（1）知识与技能：使学生理解二次函数的概念，掌握根据实际问题列出二次函数关系式的方法，并了解如何根据实际问题确定自变量的取值范围。

（2）过程与方法：复习旧知，通过实际问题的引入，经历二次函数概念的探索过程，提高学生解决问题的能力．（3）情感、态度与价值观：通过观察、操作、交流归纳等数学活动加深对二次函数概念的理解，发展学生的数学思维，增强学好数学的愿望与信心．3、教学重点：对二次函数概念的理解。

4、教学难点：由实际问题确定函数解析式和确定自变量的取值范围。

三、教法学法设计：1、从创设情境入手，通过知识再现，孕伏教学过程2、从学生活动出发，通过以旧引新，顺势教学过程3、利用探索、研究手段，通过思维深入，领悟教学过程四、教学过程：（一）复习提问1．什么叫函数？我们之前学过了那些函数？（一次函数，正比例函数，反比例函数）2．它们的形式是怎样的?(=x+b，≠0；=x,≠0；=,≠0)3．一次函数(=x+b)的自变量是什么？函数是什么？常量是什么？为什么要有≠0的条件？值对函数性质有什么影响？【设计意图】复习这些问题是为了帮助学生弄清自变量、函数、常量等概念，加深对函数定义的理解．强调≠0的条件，以备与二次函数中的a进行比较．（二）引入新课函数是研究两个变量在某变化过程中的相互关系，我们已学过正比例函数，反比例函数和一次函数。