当前位置：文档之家 › 1-2高斯定理

1-2高斯定理

  • 格式：ppt
  • 大小：1020.50 KB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

第4章-2-高斯定理

第4章-2-高斯定理
第二节 静电场的高斯定理 7-3
第四章 第七章
§4.2
静电场的高斯定理 基本内容： 基本内容：
一、电场线 二、电场强度通量 三、高斯定理
第二节 静电场的高斯定理 7-3 一. 规定 电场线
第四章 第七章
1） 曲线上每一点切线方向为该点电场方向, 曲线上每一点切线方向为该点电场方向, 切线方向为该点电场方向 通过垂直于电场方向单位面积 垂直于电场方向单位面积电场线的条 2） 通过垂直于电场方向单位面积电场线的条 数为该点电场强度的大小. 数为该点电场强度的大小.
第四章 第七章
一对不等量异号点电荷的电场线
2q
q
第二节 静电场的高斯定理 7-3
第四章 第七章
带电平行板电容器的电场线 + + + + + + + + + + + +
第二节 静电场的高斯定理 7-3
第四章 第七章
电场线的特点
始于正电荷,止于负电荷(或来自无穷远, 1） 始于正电荷,止于负电荷(或来自无穷远,去 向无穷远) 不会在没有电荷处中断. 向无穷远)，不会在没有电荷处中断. 电场线不相交. 2） 电场线不相交. 静电场电场线不闭合. 3） 静电场电场线不闭合. 电场线不仅能够表示电场强度的方向， 4) 电场线不仅能够表示电场强度的方向，而且 电场线在空间的密度分布还能表示电场强度的大小。 电场线在空间的密度分布还能表示电场强度的大小。
dS＇dS
+
任取两个球面， 任取两个球面，一 个包围曲面， 个包围曲面，另一 个在曲面内： 个在曲面内：则两 个球面的电通量都 q/ε 为q/ε0
通过任意形状的包围点电 的闭合面的电通量等于q/ q/ε 荷q的闭合面的电通量等于q/ε0

第2章--电磁场基本方程---2

第2章--电磁场基本方程---2

B(z) 0Ia
4π
2π 0
(z2
ez a a2 )3/2
d
'
0 Ia 2
2(z2 a2 )3/ 2
可见，线电流圆环轴线上的磁感应强度只有轴向分量，这是因为
圆环上各对称点处的电流元在场点P产生的磁感应强度的径向分 量相互抵消。
在圆环的中心点上，z = 0，磁感应强度最大，即
B(0)
ez
0 I
dB (r )
0
4π
Idl (r r r3
r )
体电流产生的磁感应强度
B(r ) 0 J (r) R dV
4π V R3 面电流产生的磁感应强度
z
C Idl M
r R r y
o
x
B(r ) 0
4π
S
JS
(r ) R3
R
dS
25
电磁场
第二章 电磁场基本方程
3. 几种典型电流分布的磁感应强度
D
rˆ
q
4r 2
4
电磁场
第二章 电磁场基本方程
电通量为
S
D
ds
q
4r 2
4r 2
q
此通量仅取决于点电荷量q, 而与所取球面的半径无关。
如果在封闭面内的电荷不止一个, 则利用叠加原理知, 穿出封闭 面的电通量总和等于此面所包围的总电量
S D ds Q
－－－ 高斯定理的积分形式(1839
K .F .Gauss导出),
r1 R12 r2
o
x
C2
I2dl2
y
安培磁力定律
F12
0
4π
I2dl2 (I1dl1 R12 )

高斯定理(高斯定理是什么？高斯定理怎么用？)

高斯定理(高斯定理是什么？高斯定理怎么用？)
解 对称性分析：E垂直平面
选取闭合的柱形高斯面
E dS S＇
S
0 底面积
2S＇E S＇
E
S＇
0
S＇ E
S＇
E 20

E



EE
E
E 2 0
E
x
O
( 0)
讨论
无的 限电 大场 带叠 电加 平问 面题


0

0
高斯定理举例：
均匀带电球面（球体、球壳等）的 电场分布 均匀带电直线（圆柱面、圆柱体等）
的电场分布 均匀带电无限大平面的电场分布
例：均匀带电球壳的电场强度
一半径为R , 均匀带电 Q 的薄
球壳 . 求球壳内外任意点的电场强
度. 解（1）0 r R
r S +
r +
+
O
+ 1+ + +
+R +
S
s (柱面）
h 0
2 rhE h 0

E
2 0 r
z
+
+
r h
+
+o
x+
E y en
E
O
r
讨论
o
E O
无限长均匀带电柱面的电场分布
对称性分析: 视为 无限长均匀带电直 线的集合；
r
P
dE '
选同轴圆柱型高斯 面；
由高斯定理计算
dE
dE dE'
0 rR
高斯 Carl Friedrich
Gauss 德国 1777～1855 数学家、天文学家

2.大学物理-高斯定理

2.大学物理-高斯定理

关于高斯定理的讨论：
es
1 E dS q内
s
0
3. 利用高斯定理可方便求解具有某些对称分布的静电场 成立条件：静电场
求解条件：电场分布具有某些对称性
才能找到恰当的高斯面，使 s E cos dS 中的 E和 cos 能够提到积分号外，从而简便地求出 E 分布
能否用高斯定理求电场分布？
如果不能，是否意味着高斯定理失效？
q内 ( r ) dV
R ,r
dV L 2rdr
[例三] 无限大均匀带电平面的电场（电荷面密度 ）
对称性分析： 视为无限长均匀带电直线的集合
dE
x

dE
P
' dE
dE
E方向 垂直于带电平面，
E cos0 dS E cos0 dS E cos dS 2 E 2S
左 右 侧

0

0
2 0
E
o

x
2 0
E 2 0
其指向由 号决定

的符
讨论： 1.电荷均匀分布无限大平板（厚度 h 0 ）的电场。
2.电荷分层均匀分布分层均匀无限大平板（厚度
讨论：
1. 无限长均匀带电柱面的电场分布
对称性分析：视 为无限长均匀带 电直线的集合； 选高斯面；同轴 圆柱面
R

o o
r
r
P
E o R r
' dE
P
dE
' dE dE
由高斯定理计算
r R: E0 r R:
E 2 0 r
2. 计算均匀带电圆柱层（ R1 , R2 , ）的电场分布

高斯定理1+2+

高斯定理1+2+

高斯定理1+2+ (100)Gauss定理Gauss定理是由十九世纪德国数学家卡尔·弗里德里希·高斯在他的1786年著作中推导出来的一个重要定理，被称为高斯定理或高斯求和定理，它可以利用数学表达式用简洁的方式表达出某些数字的和，也可以用于算出一定范围内正整数的和。

一、高斯定理的基本定义高斯定理的基本定义是：若将一个事物的数目N连续排列，用符号S表示这个事物的和，则S可以用如下公式表示：S=N (N+1) / 2二、高斯定理的应用1、高斯定理可以用来求正整数序列的和。

例如：若有如下正整数序列：1,2,3, ..., 98, 99, 100，则用高斯定理求该序列的和为：S=100 (101) / 2=50502、高斯定理也可以用来求负整数序列的和。

例如：若有如下负整数序列：-1、-2、-3、...、-98, -99, -100，则用高斯定理求该序列的和为：S=（-100）（-101）/ 2 = -50503、高斯定理还可以用来解决数列的乘积与求余数的问题。

例如：对于代数方程组a+b = 15，a*b = 56，则可以用高斯定理进行求解：a+b = 15a*b = 56即可求得a = 7,b = 8四、高斯定理的推广1、求和高斯定理的推广：高斯定理的推广就是求和定理，对于于数字序列m, m + r, …, m + (n-1)r，可用下列公式进行求和:Sn = (n/2)*[2m + (n-1)r]其中n为数字序列中元素的总数。

例如：对于序列2, 4, 6, 8, 10中元素的和，可运用求和定理，得：Sn = (5/2)*[2*2 + (5-1)*2] = 302、积分高斯定理的推广：高斯定理的推广就是积分定理，对于于函数y = f(x)在[a, b]上的定积分，可用如下公式进行求解：I = (b - a) / 2 * [f(a) + f(b) + 2Σf(x)]，其中f(x)为离散函数，a、b分别为函数f(x)定积分的下上限，n为f(x)函数离散点的个数。

9-1-2静电场-高斯定理

9-1-2静电场-高斯定理
S
0
q
i
i
10
关于高斯定律的说明:
(1)高斯定理表明静电场是有源场,电荷是静电场的源头. q3 q 2 qi S (2)高斯定理表达式: E dS i q1 0 S 式中 E 是面S 内、外所有电荷产生的合场强. 对闭合面的电通量 E dS 仅S面内的电荷有贡献.
S
(3)表达式中的qi是被面S包围在面内的电荷的代数和. (4)表达式的右端是封闭面S上的电场强度 E的通量e (有出有进).
11
关于高斯定律的用途： 1.当电荷分布具有某种对称性时，可用高斯定律求 出该电荷系统的电场的分布。比用库仑定律简便. 2. 当已知场强分布时,用高斯定律求出任一区域的电荷, 电势分布.
B. Q / 6
a 2
Q O
a
C. Q / 6 0
D. Q / 0 E. 条件不足，无法计算
a
17
利用高斯定律求静电场的分布
高斯定律可以用来求解特殊对称情况下的电场强度， 求解步骤如下： 1.根据电荷分布的对称性，分析电场分布的对称性。 2.根据高斯定律计算场强数值: 关键是高斯面的选取。 可以找到一个封闭曲面(高斯面), 使高斯面上 E dS
i E d s qi

S1
r
E
O
p E ds
r
S2
Φe
E 20 r
侧面
E dS E
dS E 2rl
1
侧面
0
l
24 请同学们画出 E r 关系曲线
例: 求无限长均匀带电圆筒的场强分布. 解： 该电场分布具有轴对称性.如图取同轴柱面为高斯面
A. 1 2，s q / 0 B. 1 2，s 2q / 0

§2.高斯定理(Gauss theorem)

§2.高斯定理(Gauss theorem)

q ee E d s ds 2 40r s s q q 2 4 r 2 40r 0 思考：q不在球心，
曲面不是球面，
曲面内有多个电荷，
q在球心。
dS
e ?
q
0
0 其中： qi 曲面内电荷的代数和。 E 为闭合曲面（高斯面）上的场强。
和
两均匀带电球壳如图，求电场分布。设场点距球心为r.
解：
(1)当r R1时，作高斯面如图。有：
1q. 1R
1 ( r球面）
E COSdS
E1 0
q
0
r
R2.q2
( r球面）
(2)同理，当R1 r R2时有：
q

E2 cos dS
0
E2 .4r
n
θ
若为非匀强场，任意曲面，
dS
则可用微元法求φ，见图：
d EdS cos
E cosdS
3.的正负：
对闭合曲面法线方向规定向外。
s
0 s theorem)
1.导出：特例，求点电荷q的φe。
如图，封闭面为球面，
n
在上.下底面上 0 0 而且E为常量 有：
(S )
2
即： 2 ES
E cosdS E cos dS 2ES
（.上，下底）
0
S
E 2 0
1 2 e E We e dV 2 （4） (v)
(3) 求 平行板电容器间的场强. 面电荷密度为
2
0
q1
即E2
40 r
q1
2
(3)当r R2时。
E
3

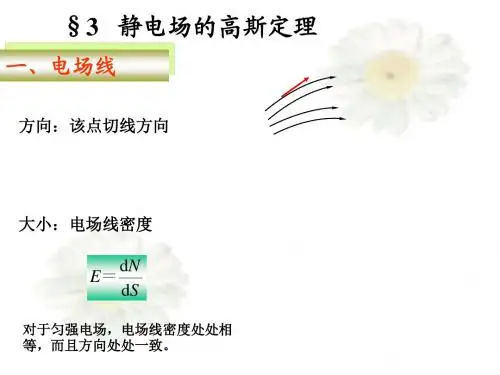
2电通量 高斯定理

2电通量 高斯定理

小结
1、点电荷
E q 4 0 r 2
2、均匀带电球面
0 q E 2 4 r 0
rR rR
3、均匀带电球体
E E
qr 40 R q 40 r
2 3
,r R ,r R
4、无限长均匀带电直线
E 20 r
5、无限长均匀带电圆柱面
6、无限长均匀带电圆柱体
· Q
· q
D
练习 一个带电量为q的点电荷位于立方体的中心处， 则通过侧面a b c d的电场强度通量等于：
q 1） 6 0 q 2） 12 0 q 3） 24 0 q 4） 48 0
· q
A
练习 一个带电量为q的点电荷位于立方体的顶角处， 则通过侧面a b c d的电场强度通量等于：
q 1） 6 0 q 2） 12 0 q 3） 24 0 q 4） 48 0
q1 q2
S
E ds：
q
内
：
S 内的净电荷
通过S的电通量， 只有S内电荷有贡献
2、 揭示了静电场中“场”和“源”的关系
q : 发出 q 0 条电场线，是电场线的“头”
q : 吸收 q 0 条电场线，是电场线的“尾”
静电场的重要性质 —— 静电场是有源场
四、高斯定理的应用
Q1 Q2 1） 2 4 0 r
3） 2 4 0 r 4） 2 4 0 r Q2 Q1
Q1 Q2 2） 2 4 0 r
Q1 R1 r
Q2
· P
（3）
R2
练习
一点电荷 , 放在球形高斯面的中心处 . 下列那 一种情况,通过高斯面的电通量发生变化:
A) 将另一点电荷放在高斯面外. B) 将另一点电荷放进高斯面内. C) 将球心处的点电荷移开,但仍在在高斯面内. D) 将高斯面半径缩小.

高斯定理的证明

高斯定理的证明
高斯定理的证明：
1. 通过包围点电荷 q 的同心球面 S 的电 通量 e 等于？ 球面上各点的场强方向与其径向相同。 球面上各点的场强大小由库仑定律给出。
1 q d e E dS EdS dS 2 4 0 r
q
E r
q q q e d e dS dS 2 2 S S 4 r S 4 r 0 0 0
dS dS cos d 2 2 r r

E
dS
dS
④.一闭合曲面对面内一点所 d 张的立体角： 4 0 对面外一点所张的立体角：
ˆ r
d e
q 40
d
e
s
q 40
d
q
0
实际上因为电力线不会中断（连续性），所以 通过闭合曲面 S 和S '的电力线数目是相等的。
E
dS ''
e E dS ( E1 E2 E3 )dS
S
1. 高斯定律中的场强 E 是由S面内和S面外全部电荷 产生的总场强，并非仅由S面内的电荷产生。 2.通过闭合曲面的电通量只决定于它所包含的电荷， 闭合曲面外的电荷对电通量无贡献。 3. q 是代数和。当 q 0 时，表示两种含义：的确无 电荷；或是有电荷但正负电荷代数和为零。
3. 通过不包围点电荷的任一闭合曲面 S 的电通量恒等于？ 由于电力线的连续性可知，穿 入与穿出任一闭合曲面的电通 dS ' 量应该相等。所以当闭合曲面 q 无电荷时，电通量为零。
4. 多个点电荷的电通量等于它们单独存在 时的电通量的代数和。
S 1 e S E dS e1 e 2 en qi 0 i

晶体管原理 (1-2)

晶体管原理 (1-2)

得 ：
kT 将 = 0.026V, ND1 =1×1020 cm−3, ND2 =1×1016 cm−3 q 代 ， ： bi = 0.026ln(104 ) = 0.24V 入 得 V
7、由第6 题： kT 1 dn kT 1 dN(x) E =− ⋅ ⋅ =− ⋅ ⋅ q n dx q N(x) dx x kT 将 N(x) = N0 exp(− ) 代入，得：E = λ qλ kT 再将 = 0.026 V, λ = 0.4µm 代入，得：E = 650 V cm q 2qN0Vbi 突变结 的最大电场强度表达式为：| Emax |= εs N N kT N N N 式中： 0 = D A ≈ ND =1015 cm−3, Vbi = ln D 2 A = 0.757V, ND + NA q ni q =1.6×10−19 C, εS =1.045×10−12 F cm, 代入 | Emax | 中，得：| Emax |=1.52×104 V cm
34、 、
已知 对于 单边突 变结 ， εsqN0 K CT = A = 1 2(Vbi −V ) (Vbi −V ) 2 K 当 Vbi = 0.6V, V = −3V时 CT = ， =10 pF, 由此 可得 3.6 K =10 3.6, 因此 V = 0.2V时 当 ， 10 3.6 CT = =10 9 = 30 (pF) 0.4
qDEni2 qVBE AEq2DEni2 qVBE JpE = WE exp kT −1 = Q exp kT −1 EO ∫ NEdx
0
再根据注入效率的定义，可得： 再根据注入效率的定义，可得：
JpE QBODE JnE JnE γ= = = 1+ = 1+ JE JnE + JpE JnE QBEDB

第二讲-高斯定理

第二讲-高斯定理

rR rR
无限长均匀带电圆柱体
r
E
2 0
R
2
20r
rR rR
无限长均匀分布带电直线
E
2 0r
上页 下页 返回 退出
家庭作业：8-6、8-8、8-11、8-12、8-13
上页 下页 返回 退出
s1
s2
s3
ER2 0 R2 E
=0
n
n
S1
ds
S2
S3
n
R ds E
上页 下页 返回 退出
1. 求均匀电场中二分之一球面旳电通量。
S
Y
2.
在均匀电场
E
3i
2
面积为S旳电通量。
n
E
n
j
中n，过YEOZ平面n 内
S1
R
O
X
Z
E •S
O n
S2
S1 S2 0
( 3i 2 j )• Si 3S
2ES0
高斯面内有： qi内 S0
0
0
E
n
2 0
无限大带电平面旳电场是均匀电场
上页 下页 返回 退出
E
n
2 0
推论：
( 0)
无限大带电平面旳电场是均匀电场。
两个无限大带等量异号均匀电荷旳平行平面旳电场。
0 0
· E E A
·E
C E
·
E
E
B
A、B点旳场强：
EA EB
E
电场中经过某一曲面（平面） 旳电场线条数称 经过该曲面（平面）旳电通量。
非均匀电场经过曲面 S 旳电场强度通量: en
E E • ds
θ dS

第2章 静电场(4) 高斯通量定理

第2章 静电场(4) 高斯通量定理
通量仅由面内电荷决定。
27
3、高斯定理的意义 1 e E dS
S
0
q
i
i
(1) 说明静电场是有源场，源即电荷。
q 0, e 0 , 电场线从+q 出发，+q 是源头； q 0, e 0 , 电场线止于 - q ， - q 是尾闾。
(2) 高斯定理不仅适用于静电场， 亦适用于运动电荷的电场和随时间变 化的电场，是电磁场基本定理之一。
其中， E ：电场强度， P ：电极化强度
18
其中， 0 —— 真空中的介电常数 12 ( 8.854 10 F / m)(电容率) —— 介质的介电常数 ( 0 r ) (电容率) r —— 介质的相对介电常数 ( 1 e )(相对电容率)
e
利用高斯定理求场强 E 比较方便。
(2) 常见的具有对称性分布的电荷系统：
1） 球对称（球体，球面）；
2） 柱对称（无限长柱体，无限长柱面）； 3） 面对称（无限大平板，无限大平面）。
30
(3) 求电场分布的步骤：
1) 分析带电系统的对称性； 2) 选合适的高斯面：使面上场强的大小处处 相等(或部分 相等，部分为零），场强的方 向与曲面正交或平行。 3) 利用高斯定理求场强。
—— 介质的电极化率
0
SI单位： r 、e ：(纯数)
、 0 ：C2/Nm2
(F/m)
19
介 真空 空气
质
r
1 1.00059
变压器油
瓷
2.24
68
玻璃
钛酸钡
510
103104
20
性质
(1) D是辅助物理量, E 才是真实物理量。 (2) D是一个包含了场与介质极化两种性质的量。 (3) D 线只由自由电荷决定。

电通量和高斯定理

电通量和高斯定理

05 电通量与高斯定理的意义 和影响
对电磁学理论的意义
描述电场分布
建立电磁场理论
电通量是描述电场分布的重要物理量， 通过高斯定理，我们可以计算出空间 中任意区域的电场强度和电通量密度。
电通量与高斯定理是电磁场理论中的 基础概念，为后续的麦克斯韦方程组 等理论奠定了基础。
揭示电场性质
高斯定理揭示了电场的一个重要性质， 即电场线总是闭合的，这一性质对于 理解电场的产生和传播机制具有重要 意义。
散度定理法
利用散度定理计算电通量， 公式为：∮E⋅dS=∫E⋅dS。
微元法
将闭合曲面划分为若干个 小面元，分别计算每个面 元的电通量，最后求和得 到总电通量。
02 高斯定理的表述
定理的表述
高斯定理的表述
在封闭曲面S内，总电荷量Q等于该封闭曲面内电通量Φ的积分， 即 ∫∫Σ Q = ∫∫Σ dΦ。
电通量的物理意义
表示电场分布的特性
电通量的大小反映了电场在某个闭合 曲面上的分布情况，可以用来描述电 场的强弱和方向。
与电荷分布的关系
电通量的大小与电荷分布有关，电荷 分布的不同会导致电通量的变化。
电通量的计算方法
01
02
03
公式法
根据电场强度E和闭合曲 面S的面积S，计算电通量。 公式为：Φ=∫∫E⋅dS。
要点一
总结词
要点二
详细描述
高斯定理是求解电场的强大工具，通过合理选择高斯面可 以简化问题求解过程。
高斯定理表述为：“通过任意闭合曲面的电场强度通量等 于该闭合曲面所包围的电荷量与真空电容率的比值。”在 求解电场问题时，可以根据问题的对称性和电荷分布情况 选择合适的高斯面，从而将复杂的积分运算简化为简单的 代数运算。例如，在求解无限大均匀带电平面或球壳产生 的电场时，利用高斯定理可以快速得出结果。

第五章-2 高斯定理

第五章-2 高斯定理

2q
−q
桂林电子科技大学十院
clc2000@
第五章 静电场
§5-2高斯定理 高斯定理
带电平行板电容器的电场线 + + + + + + + + + + + +
桂林电子科技大学十院
clc2000@
第五章 静电场 电场线特性
§5-2高斯定理 高斯定理
1） 始于正电荷,止于负电荷(或来自无穷远,去向 始于正电荷,止于负电荷(或来自无穷远, 无穷远) 无穷远) —— 有源 2） 电场线不相交 3） 静电场电场线不闭合 无旋
第五章 静电场
§5-2高斯定理 高斯定理
电场强度通量 高斯定理
桂林电子科技大学十院
clc2000@
第五章 静电场
一 电场线（E 线） 电场线（
为描述电场分布而人为引入的有向曲线
§5-2高斯定理 高斯定理
规 定
1） 曲线上每一点切线方向为该点电场方向 ） 曲线上每一点切线方向为该点电场方向 切线方向为该点 2） 通过垂直于电场方向单位面积电场线数（即电场线 通过垂直于电场方向单位面积电场线数（ 单位面积电场线数 疏密程度）为该点电场强度的大小 的疏密程度）为该点电场强度的大小
桂林电子科技大学十院
i ( in )
S
i ( ex )
S
S
ε0
∑
i ( in )
Qi
clc2000@
第五章 静电场 高斯定理Φ e =
总结
§5-2高斯定理 高斯定理
∫
S
v v 1 E ⋅ dS =ε0Leabharlann ∑Qi =1n
i
1）高斯面上的电场强度为所有内外电荷的总电场强度. 高斯面上的电场强度 所有内外电荷的总电场强度 面上的电场强度为 内外电荷的总电场强度. 高斯面为封闭曲面. 2）高斯面为封闭曲面. 3）穿进高斯面的电场强度通量为正，穿出为负. 穿进高斯面的电场强度通量为正，穿出为负. 仅高斯面内的电荷对高斯面的电场强度通量有贡献. 通量有贡献 4）仅高斯面内的电荷对高斯面的电场强度通量有贡献. 静电场是有源场 有源场. 5）静电场是有源场.

大学物理-高斯定理

大学物理-高斯定理
复习 库仑定律
电场强度的计算
F
1
4 0
q1q2 r2
r0
电场强度
E
F
q0
(1) 点电荷的场强
E
1 4πε0
q r2
r0
(2) 场强叠加原理
E E1 E2 En
(3) 电荷连续分布的 带电体的电场
电 荷
E dE
dq
r
(q)
(q) 4 0r 3
分 布
dq ρdV (体 分 布) dq σdS (面 分 布) dq λdl (线 分 布)
q2 A P*
s
q2 B
q1
在点电荷 和q 的q静电场中，做如下的三个闭合面
求通过各闭合S面1 ,的S电2 ,通S量3。,
Φe1
E dS
q
S1
0
Φe2 0
Φe3
q
0
q
q
S1
S2
S3
例：一点电荷位于边长为 a 的立方体的顶角上， 求：通过该立方体表面总的电通量。
解： 顶角所在的三个面上的通量为零。 其余三个面上直接计算困难
(3) 天文学和大地测量学中：如小行星轨道的计算，地球大 小和形状的理论研究等。统计 理论和误差理论，发明了最小二乘法，引入高斯误差曲线。
(5) 高斯还创立了电磁量的绝对单位制。
一、电通量 1、电场线 ( Electric Field Line ) （电场的几何描述）
E
n
dS
E
S E cos dS
Φe
E dS
S
为通过 S 面的电通量。
dS 有两个法线方向，dφ 可正可负。
S为封闭曲面
规定：闭合面上各面元的外法

高斯定理1+2+....100

高斯定理1+2+....100

高斯定理1 2 (100)高斯定理公式是即1+2+3+...+n=(首项+末项)。

高斯定理Gauss' law也称为高斯通量理论Gauss' fluxtheorem，或称作散度定理、高斯散度定理、高斯奥斯特罗格拉德斯基公式、奥氏定理或高－奥公式通常情况的高斯定理都是指该定理，也有其它同名定理。

数学的起源数学，起源于人类早期生产活动，为中国古代六艺之一，亦被古希腊学者视为哲学之起点。

数学的演进可以看成是抽象化的持续发展，或是题材的延展。

第一个被抽象化的概念是数字，其对两个苹果及两个橘子之间有某样相同事物的认知是人类思想的一大突破。

除了如何去数实际物质的数量，人类亦了解了如何去数抽象物质的数量。

高斯定理数学公式是：∮F·dS=∫(▽·F)dV。

高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。

高斯定理（Gauss' law）也称为高斯通量理论（Gauss' flux theorem），或称作散度定理、高斯散度定理、高斯－奥斯特罗格拉德斯基公式、奥氏定理或高－奥公式（通常情况的高斯定理都是指该定理，也有其它同名定理）。

高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。

因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。

扩展资料：高斯定理指出：穿过一封闭曲面的电通量与封闭曲面所包围的电荷量成正比。

换一种说法：电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比。

它表示，电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和，与曲面内电荷的位置分布情况无关，与封闭曲面外的电荷亦无关。

在真空的情况下，Σq是包围在封闭曲面内的自由电荷的代数和。

当存在介质时，Σq应理解为包围在封闭曲面内的自由电荷和极化电荷的总和。

初中数学高斯定理

初中数学高斯定理

初中数学高斯定理高斯定理，也称为高斯-斯托克斯定理，是微积分学中的一个定理。

它是利用曲面积分和向量分析的基本概念提出的，经常用于解决电场、磁场、流体力学等领域的问题。

高斯定理可以将曲面积分转化为体积积分，从而简化计算。

高斯定理的表述高斯定理可以表示为以下几种形式：1.对于封闭曲面S和任意向量场F，高斯定理为：∯s (F·n)dS = ∬∬∬V (divF)dV其中，n是曲面S上的单位法向量，dS是微元面积，divF是向量场F的发散。

2.对于无限大的截面为S的长直导体内部的电场E和电荷密度ρ，高斯定理为：∮E·ds = Q/ε0其中，Q是截面S内的总电荷量，ε0是真空介电常数，s是导体截面上的微元弧长。

∫∫∫V (divE)dV = ∫∫∫V (ρ/ε0)dV其中，ε0表示真空电容率。

高斯定理在实际问题中有着广泛的应用，下面以几个例子来说明。

1.求解电场强度高斯定理在电场强度的求解中有着重要应用。

当电荷分布对称时，高斯定理可以将曲面上的积分转换为体积内的积分，从而大大简化了计算。

例：求电荷均匀分布球壳内外的电势、场强。

先选择一个脱离球心面的球形高斯面，并经过导体上下表面的设想，表明导体表面电势相等，且在面外区域电场强度场为0，在内壳面区域电场强度场相等，则有：其中Q_e是高斯面内电荷量。

因为在球心处电场强度为0，则高斯面以外的积分为0，则：解得E={K_eQ_e}/r^2其中K_e=1/4πε0为电强度常数。

2.求解电通量利用高斯定理，我们可以计算负荷对于导体表面（不包括孔和缝）和导体中的电通量。

例：计算均匀电荷分布球体的电通量。

设有一个半径为r1的均匀带电球体，在离球心r处(小于r1)取一小球，其面积为S，则由于电场分布对称，则小球上各相等的面元二相互平行，则关于小球表面总的电力矢量可看成是在小球中心通的电通量矢量。

由Gauss定理，通量与小球的尺寸无关，有：Φ_e = E.S = Q/(4πε0r^2)×4πr^2 = Q/ε0其中Φ_e是电通量，E是电场强度，Q是球体内的总电荷量。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图 电荷线密度为 的无限长均 匀带电体
由
D dS q , 得
S
33
由
D dS q ,
S
得
D1 2rL L
D1 er 2r
D1
E1 er 0 2 0 r
D dS
S
S1
D1 dS1 D2 dS2 D3 dS3
现象。这些沿外电场方向作取向排列的电偶
极子，将使介质对外表现出宏观电矩（电偶 极子），
P pi qi d i

我们说电介质被极化了。
10
(2)静电场中的电介质被极化
E
无极性分子 有极性分子
图1.2.3 电介质的极化
电介质在外电场作用下发生极化，形成有向排列； 电介质内部和表面产生极化电荷 (polarized charge)；
极化电荷与自由电荷都是产生电场的源。
11
d
-q +q
E0 在不超过一定的强度条件下，外电场愈强，则电 偶极子电荷间的距离d愈大，其偶极矩p=qd也越大， 取向排列愈趋向于一致，表现出的宏观电矩愈强。 外电场的这个一定的电场强度称为击穿场强。
12
(3) 极化强度与极化电荷的关系
电介质在外电场E作用下发生极化，形成有向排列的电偶极矩；
( f p )( r r ' ) 1 ( f p )( r r ' ) E (r ) dV ' dS ' 3 3 S' 4 0 V ' r r' r r'
18
1.2.3. 高斯定律

一、真空中的高斯通量定理
根据库伦和叠加原理得出（高斯定理）： 在无限大真空静电场的任意闭合曲面S上，电场强 度的面积分等于曲面内的总电荷 q dV 的
V
1
0
倍（V是S限定的体积），而与曲面外电荷无关。 即
E d S dV 0 0V S
19
q
1
E d S dV 0 0V S
或者说：在真空电场中，穿出任意闭合面S的通量恒等 于闭合面内电荷的代数和除以真空的介电系数 0。 •真空中电场强度E的闭合面通量只与闭面内的电荷 和有关，而与闭面外的电荷无关。 •可以推广到体电荷、面电荷、线电荷以及点电荷 系产生的电场。
P线
思考
E 线由正电荷出发，终止于负电荷； D 线由正的自由电荷出发，终止于负的自由电荷； P 线由负的极化电荷出发，终止于正的极化电荷。
29
思考？
• 1 电场强度在电介质内部是增加了，还是 减少了？ • 2 D是否与介质无关？
D
DdV
V
V
dV
散度定理

S
D dS q
7
(1)静电场中的电介质

电介质的分子可分为极性分子和非 极性分子两类。
非极性分子：其中的正、负电荷作 用中心重合，宏观来看对外呈电中 性。在外电场作用下，分子中的正、 负电荷作用中心沿电场方向发生了 微小位移d，于是，可以等效为一 个电偶极子，电偶极矩为p=qd， 从宏观来看对外呈现电性。

8

①高斯定律是基于场的观点，从整体上来反映场 与源之间的关系，闭合曲面S可以跨多种介质，而 不受介质影响；
② D的闭合面净通量仅与闭合面内的电荷相关， 而D本身则与产生电场的所有电荷以及介质的特 性与分布情况相关。
26
（2）高斯定律的微分表达式
S D d S q dV
V
应用高斯散度定理，得 则有

电介Biblioteka 内部和表面产生极化电荷；极化电荷与自由电荷都是产生电场的源。 用极化强度P表示电介质的极化程度，即
P
V 0
lim
p
V
C/m2
电偶极矩体密度
式中 p 为体积元 V 内电偶极矩的矢量和，P 的 方向从负极化电荷指向正极化电荷。
13
一个电偶极子产生的电位：

1 4 0
p er qd cos 2 2 R 4 0 R
22
二、当有电介质存在时，
电场是自由电荷q与极化电荷qp在真空中共同产生。 运用真空中静电场的高斯定律，总的净电荷将包含 自由电荷q和极化电荷qp。

s E d S
dV q P q q V P
ε0
0
讨论闭面内的体极化电荷 ：
q p V p dV V PdV S P d S
q
1
20
E的散度
E (r )
dq (r )dV V ' V ' 4 0 r r ' 3 4 0 r r ' 3
高斯定律的微分形式
1
r r'
1
r r'
作散度运算
(r ' ) E (r ) 0
• A= 0 (无源）
• A= 0 (正源) • A= 0 (负源)

2
1-2 静电场中的导体

导体的定义：其内存在着能够自由运动的电荷的物质。 自由运动的电荷可以是自由电子或离子，金属是最常见 的导体。 当我们把导体放入外电场中，则外电场对导体内的自由 电荷将产生作用力，使它们沿着（或逆着）电场的方向 运动，导体表面会出现感应电荷。

Eex
17

根据电荷守恒原理，这两部分极化电荷的总和


V'
PdV' P en dS' 0
S'
在均匀极化的电介质内，极化电荷体密度
p 0
有电介质存在的场域中，任一点的电位及电场 强度表示为
1 (r ) 4 0 ( f p ) ( f p ) dV ' dS ' V ' S' r r' r r'
S2 S2
L
34
设距直导线距离为a处为电位参考点 空间任意点的电位:
a
a E dl er dl 20r P r
15
P( r ) en 1 ' P( r ) 1 V ' R dV' 4 0 S' R dS' 4 0
p P
极化电荷体密度
极化电荷面密度
p P en
( r ) 1 4 0

p (r ' )
R
V'
dV '
1 4 0
D 0E P 0E e 0E 0 (1 e )E r 0E E
其中
r 1 e

——相对介电常数；
——介电常数，单位（F/m）
28
例 平板电容器中有一块介质 ，画出D 、E 和 P 线分布。
E线
D线 图1.2.6 D、E 与 P 三者之间的关系
V
引入
D ε0 E P
D为电位移矢量，单位是C/m2（库/米2）。有
S D d S q dV
V
这就是高斯定律的积分表达式。
25
S D d S q dV
V
高斯定律的积分表达式:它表明D的通量只与闭合曲面 S内的自由电荷有关，而与介质的极化无关，也与介 质结构、状态、分布无关。 理解高斯定律应注意：
E
极性分子：其中的正、负电荷 作用中心本来就不重合，即每 一个极性分子的电特性都可以 用一电偶极子来等效反映，但 其电偶极矩的分布杂乱无章， 互相抵消，宏观来看对外仍然 呈电中性。在外电场作用下， 极性分子的电偶极矩沿外电场 的方向发生偏转，将趋向于有 序的排列，从宏观来看对外呈 现电性。
9

处在电场中的电介质，在电场力的作用下其 分子发生的这种变化现象称为电介质的极化
23
（1）高斯定律的积分表达式
s E d S
dV qP q q V P
ε0
0
q p V p dV V PdV S P d S
代入得积分式
ε0 S E d S q S P d S
24
S ( ε0 E P ) d S q dV
E 。 0
5
接地导体都不带电。（
） ）
一导体的电位为零，则该导体不带电。 （
任何导体，只要它们带电量不变，则其电位是不变的。 （
6
１.2.2 静电场中的电介质
定义：其内部存在的带电粒子，受到原子内
在力、分子内在力或分子之间的作用力不能 自由运动，这样的物质称为电介质（简称介 质）。 介质中这些粒子所带的电荷称为束缚电荷。 上面的定义表现了电介质的主要特征，忽略 了它微弱的导电性。
30
D 的通量与介质无关，但不能认为D 的分布与介质无关。

S1
D1 dS ( q )
(

S2
q) D2 dS
(
q D1 D2 D3 2 4r
图
)
点电荷的电场中置入任意一块介质
D 通量只取决于高斯面内的自由电荷，而高斯面上的 D 是由高斯面内、外的系统所有电荷共同产生的。
图均匀场中放进了介质球的电场
图 均匀场中放进了导体球的电场
1
2.2 静电场中的导体与电介质
前面我们讨论了在真空中不同分布形式的电荷产生 的电场， 实际的电场分布还与电场空间存在的物质有关。 根据导电性能，我们可把物质粗分为两大类：导体 与电介质。 导体在电场作用下产生的静电感应现象； 电介质在电场作用下产生的极化现象，都会影响空 间电场的分布。