下载文档原格式
关于静电场的高斯定理和静电场的环路定理静电场的高斯定理和静电场的环路定理是库仑定律的推论，所以称之为定理。
由于库仑定律是静电场的基本规律，适用于静电场，所以库仑定律的推论也适用于静电场。
电场有许多种：静电场（由静止电荷激发）、恒定电场（由运动然而空间分布不随时间改变的电荷体系激发的电场）、位电场（可以在其中建立电位函数的电场，位电场的电场强度等于电位的负梯度，分为恒定的与时变的，静电场和恒定电场就属于恒定的位电场）、涡旋电场。
静电场的高斯定理的文字表述是：静电场中，电场强度穿出闭合曲面的通量等于该闭合曲面所包围的总电量除以真空电容率。
静电场的高斯定理的数学表述式是：in 0d i S qE S ε⋅=∑⎰ 。
英国著名物理学家麦克斯韦首先假设静电场的高斯定理的数学表示式in 0d i S q E S ε⋅=∑⎰ 适用于一切电场，也就是说，实际的电场强度（即总电场强度）穿出闭合曲面的通量等于闭合曲面内的总电量除以真空电容率。
这个假设后来被实验证实了。
正因为这个原因，数学表示式in 0d i S qE S ε⋅=∑⎰ 也叫做高斯定律。
由于德国数学家高斯根据库仑定律推出的这个静电场规律的数学表示式是普遍适用的，这让高斯在电磁学中享有很高的声誉。
in 0d i S q E S ε⋅=∑⎰ 有好几个称谓：高斯定理、高斯通量定理、电场的高斯定理、电场的高斯通量定理、高斯定律、高斯通量定律、电场的高斯定律、电场的高斯通量定律。
对于静电场，这个规律叫做静电场的高斯定理，或者静电场的高斯通量定理。
高斯在数学方面有一项重要成就，叫做高斯公式（也可以叫做高斯通量公式或者高斯散度公式）。
高斯公式的数学表示式是d d S Vf S f V ⋅=∇⋅⎰⎰ 。
其含义是：矢量场穿出闭合曲面的通量等于矢量场的散度在闭合曲面所包围的空间区域内的体积分。
高斯定理是电（磁）学规律，高斯公式是纯粹数学规律，两者截然不同。
但是把两者结合起来，就可以推出0E ρε∇⋅= 。
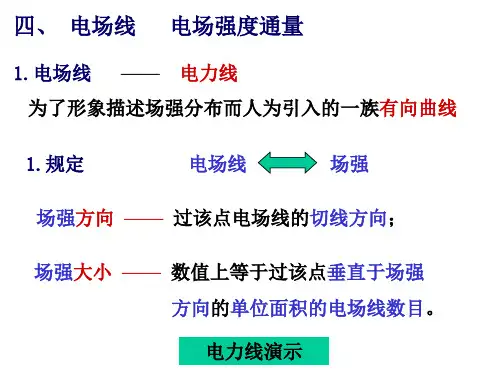
静电场中的高斯定理：高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。
可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。
表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ （1）高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。
根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。
选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。
最后由高斯定理求出场强。
高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。
但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。
下面举一些例子来说静电场中高定理的应用：例1：一半径为R 的带电球体，其电荷体密度分布为()Ar r R ρ=≤，0()r R ρ=>，A 为大于零的常量。
真空中静电场的高斯定理
真空中静电场高斯定理：在真空静电场中，通过任意的闭合曲面电通量等于该闭合曲面内所包围的电荷的代数和除以真空介电常量。
电通量Φ所代表的物理含义是通过电场中某一给定曲面的电场线的总条数。
在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
静电场中的高斯定理：高斯定理是静电学中的一个主要定理, 它反应了静电场的一个基赋性质, 即静电场是有源场, 其源等于电荷.可表述为: 在静电场中, 经由过程随意率性闭合曲面的电通量, 等于该闭合曲面所包抄的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关.表达式为01()1/ni i S E ds q φε==•=∑⎰⎰ （1）高斯定理是用来求场强 E 散布, 定理中, S 是随意率性曲面, 因为数学程度的限制, 要由高斯定理盘算出E,则对由场的散布有必定的请求, 即电荷散布具有严厉的对称性( 若电荷散布不合错误称性即不是平均的, 引起电场散布不合错误称, 不克不及从高斯定理求空间场强散布,高斯定应当然仍是成立的) , 因为电荷散布的对称性导致场强散布的对称性, 场强散布的对称性应包含大小和偏向两个方面.典范情形有三种:1) 球对称性, 如点电荷, 平均带电球面或球体等;2) 轴对称性, 如无穷长平均带电直线, 无穷长平均带电圆柱或圆柱面, 无穷长平均带电同轴圆柱面3) 面临称性, 如平均带电无穷大平面或平板,或者若干平均带电无穷大平行平面.依据高斯定理盘算场强时, 必须先依据电荷散布的对称性, 剖析场强散布的对称性; 再恰当拔取无厚度的几何面作为高斯面.拔取的原则是:○1待求场强的场点必须在高斯面上;○2使高斯面的各个部分或者与E 垂直, 或者E 平行;○3与E 垂直的那部分高斯面上各点的场强应相等;○4高斯面的外形应是最简略的几何面.最后由高斯定理求出场强.高斯定理解释的是经由过程闭合曲面的电通量与闭合 曲面所包抄的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包抄的电荷有关, 但与曲面内电荷的散布无关.但闭合曲面上的电场强度倒是与曲面表里所有电荷相接洽的,是配合激发的成果.下面举一些例子来说静电场中高定理的运用：例1：一半径为R 的带电球体,其电荷体密度散布为()Ar r R ρ=≤,0()r R ρ=>,A 为大于零的常量.试求球体表里的场强散布及其偏向.解：在球内取半径为r .厚为d r 的薄球壳,该壳内所包含的电荷为23d d 4d 4d q V Ar r r Ar r ρ==⋅π=π在径为r 的球面内包含的总电荷为以该球面为高斯面,按高斯定理有0421/4εAr r E π=π⋅得到()0214/εAr E =,(r≤R)偏向沿径向向外在球体外作一半径为r 的齐心高斯球面,按高斯定理有得到()20424/r AR E ε=,()r R >偏向沿径向向外例题2:有两个齐心的平均带电球面,半径分离为1R .2R )(21R R <,若大球面的面电荷密度为σ,且大球面外的电场强度为零,求：（1）小球面上的面电荷密度;（2）大球面内各点的电场强度. 解:（1）设小球面上的电荷密度为σ',在大球面外作齐心的球面为高斯面,由高斯定理： 0'1220int 4'4d επσπσεR R q S E S⋅+⋅==⋅⎰⎰ ∵大球面外0=E∴2221440R R σπσπ'⋅+⋅= 解得： 221()RR σσ'=-（2） 大球面内各点的场强两个平均带电球面场强的迭加:内部场强为零,外部相当点电荷在1r R <区域：00021=+=+=E E E在12R r R <<区域：2112204'04R E E E r πσπε=+=+=220⎪⎭⎫ ⎝⎛-r R εσ 2 对高斯定理的几点解释高斯定理是电磁学中的主要定理之一.其数学表达式为它暗示经由过程闭合曲面的电通量等于该闭合曲面内电荷代数和的01ε倍.。
