第九章 吸收
- 格式:doc
- 大小:770.50 KB
- 文档页数:15


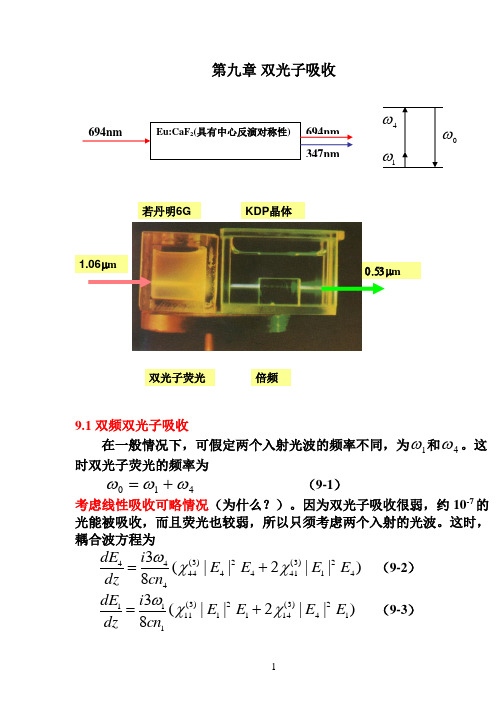
第九章 双光子吸收9.1 双频双光子吸收在一般情况下,可假定两个入射光波的频率不同,为1ω和4ω。
这时双光子荧光的频率为410ωωω+= (9-1)考虑线性吸收可略情况(为什么?)。
因为双光子吸收很弱,约10-7的光能被吸收,而且荧光也较弱,所以只须考虑两个入射的光波。
这时,耦合波方程为)||2||(83421)3(41424)3(44444E E E E cn i dz dE χχω+= (9-2) )||2||(83124)3(14121)3(11111E E E E cn i dz dE χχω+= (9-3) 1.06μm若丹明6G KDP 晶体双光子荧光 倍频0.53μm或421)3(4144424)3(44444||43||83E E cn i E E cn i dz dE χωχω+= (9-4) 124)3(1411121)3(11111||43||83E E cn i E E cn i dz dE χωχω+= (9-5)用*4E 乘(9-4)两边,用*1E 乘(9-5)两边,得2421)3(414444)3(44444*4||||43||83E E cn i E cn i dz dE E χωχω+=(9-6)2124)3(141141)3(11111*1||||43||83E E cn i E cn i dz dE E χωχω+= (9-7)两边取共轭,得(根据上图及(9-1)式,1ω,4ω,11ωω+,44ωω+皆 远离介质的共振频率,)3(44χ和)3(11χ皆为实数)2421*)3(414444)3(4444*44||||43||83E E cn i E cn i dz dE E χωχω--=(9-8)2124*)3(141141)3(1111*11||||43||83E E cn i E cn i dz dE E χωχω--= (9-9)(9-6)+(9-8),(9-7)+(9-9)得2421")3(414424||||23||E E cn dz E d χω-= (9-10) 2124")3(141121||||23||E E cn dz E d χω-= (9-11)")3(41χ是)3(41χ的虚部,")3(14χ是)3(14χ的虚部。


第八章传质过程导论第九章气体吸收1-1 吸收过程概述与气液平衡关系1-1 在25℃及总压为101.3kPa的条件下,氨水溶液的相平衡关系为p*=93.90x kPa。
试求(1) 100g水中溶解1g的氨时溶液上方氨气的平衡分压和溶解度系数H;(2) 相平衡常数m。
1-2 已知在20℃和101.3kPa下,测得氨在水中的溶解度数据为:溶液上方氨平衡分压为0.8kPa时,气体在液体中溶解度为1g (NH3)/1000g(H2O)。
试求在此温度和压力下,亨利系数E、相平衡常数m及溶解度系数H。
1-3 在总压为101.3kPa,温度为30℃的条件下,含有15%(体积%)SO2的混合空气与含有0.2%(体积%)SO2的水溶液接触,试判断SO2的传递方向。
已知操作条件下相平衡常数m=47.9。
1-2 传质机理1-4 组分A通过厚度为的气膜扩散到催化剂表面时,立即发生化学反应:,生成的B离开催化剂表面向气相扩散。
试推导稳态扩散条件下组分A、B的扩散通量及。
1-5 假定某一块地板上洒有一层厚度为1mm的水,水温为297K,欲将这层水在297K的静止空气中蒸干,试求所需时间为若干。
已知气相总压为101.3kPa,空气湿含量为0.002kg/(kg 干空气),297K时水的饱和蒸汽压为22.38 kPa。
假设水的蒸发扩散距离为5mm。
1-3 吸收速率1-6 采用填料塔用清水逆流吸收混于空气中的CO2。
已知25℃时CO2在水中的亨利系数为1.66×105kPa,现空气中CO2的体积分率为0.06。
操作条件为25℃、506.6kPa,吸收液中CO2的组成为。
试求塔底处吸收总推动力∆p、∆c、∆ X和∆ Y。
1-7 在101.3kPa及20℃的条件下,在填料塔中用清水逆流吸收混于空气中的甲醇蒸汽。
若在操作条件下平衡关系符合亨利定律,甲醇在水中的溶解度系数H=1.995kmol/(m3·kPa)。
塔内某截面处甲醇的气相分压为6kPa,液相组成为2.5 kmol/m3,液膜吸收系数k L=2.08×10-5m/s,气相总吸收系数K G=1.122×105 kmol/(m2·s·kPa)。

第一节概述一、什么是吸收?吸收是利用气体混合物中各组分在某种溶剂中溶解度的差异,而将气体混合物中组分加以分离的单元操作。
溶质: 气体混合物中能溶解的组分称为溶质,以A表示;惰性组分: 不溶或微溶组分称为惰性组分或载体,以B表示;溶剂: 吸收过程所用的溶剂称为吸收剂,以S表示;吸收液: 所得的溶液称为吸收液。
二、吸收在石油化工中的应用(1)回收有用组分(2)制取液态产品(3)净化气体(废气治理)三、吸收的工艺流程四、吸收分类按溶质和溶剂之间是否发生明显的化学反应吸收按溶于溶剂的组分数吸收按吸收过程是否发生明显的温度变化吸收五、吸收剂的选择1.溶解度大;2.选择性好;3.挥发度低;4.粘度低;5.无毒、无腐蚀;6.吸收剂应尽可能不易燃、不易发泡、价廉易得、稳定。
第二节吸收过程的相平衡关系一、气体在液体中的溶解度在一定的温度与压力下、使气体混合物与一定量的溶剂接触,气相中的溶质便向液相中的溶质转移,直至液相中溶质达到饱和为止,这时,我们称之为达到了相平衡状态。
达到了相平衡状态时气相中溶质的分压,成平衡分压;液相中溶质的浓度称为平衡浓度(或溶解度)。
大量实验表明,溶解度和气相中溶质的分压有关。
从图上可以看出:分压高,溶解度大温度高,溶解度小吸收操作应在低温高压下进行,脱吸应在高温、低压下进行二、亨利定律1.亨利定律在一定的温度下,当总压不很高(<500kpa)时,稀溶液上方溶质的平衡分压与该溶质在液相中的摩尔分率成正比,其表达式如下式中------溶质在气相中的平衡分压,KN/m2;------溶质在液相中的摩尔分率;E------亨利系数,。
式(9-1)称为亨利(Henry)定律。
亨利系数E值由实验测定,常见物系的E值可由有关手册查出。
当物系一定时,亨利系数随温度而变化。
一般说来,值随温度升高而增大,这说明气体的溶解度随温度升高而减小,易溶气体值小,难溶气体的值大。
2.用溶解度系数表示的亨利定律若将亨利定律表示成溶质在液相中的摩尔浓度与其在气相中的平衡分压之间的关系,则可写成如下形式(9-2)式中C──液相中溶质的摩尔浓度,kmol/m3H──溶解度系数,溶液中溶质的摩尔浓度和摩尔分率及溶液的总摩尔浓度之间的关系为(9-3)把上式代入式(9-2)可得将上式与式(9-1)比较,可得(9-4)溶液的总摩尔浓度可用1m3溶液为基准来计算,即(9-5)式中──溶液的密度(kg/m3)──溶液的摩尔质量。
第九章吸收本章学习要求1.掌握的内容相组成的表示方法及换算;气体在液体中的溶解度,亨利定律各种表达式及相互间的关系;相平衡的应用;分子扩散、菲克定律及其在等分子反向扩散和单向扩散的应用;对流传质概念;双膜理论要点;吸收塔的物料衡算、操作线方程及图示方法;最小液气比概念及吸收剂用量的确定;填料层高度的计算,传质单元高度与传质单元数的定义、物理意义、传质单元数的计算。
2.熟悉的内容各种形式的传质速率方程、传质系数和传质推动力的对应关系;各种传质系数间的关系;气膜控制与液膜控制;吸收剂的选择。
3.了解的内容分子扩散系数及影响因素。
第1节概述9.1.1.气体吸收过程和工业应用1.吸收吸收~利用混合气体中各组份在同一种液体(溶剂)中溶解度差异而实现组分分离的过程称为气体吸收。
2.吸收操作在化工生产中的应用(1)分离混合气体以获得一定的组分。
(2)除去有害组分以净化气体。
(3)制备某种气体的溶液。
(4)保护环境。
3.吸收与脱吸作为一种完整的分离方法,吸收过程应包括“吸收”和“脱吸”两个步骤。
“吸收”仅起到把溶质从混合气体中分出的作用,在塔底得到的是由溶剂和溶质组成的混合液,此液相混合物还需进行“脱吸”才能得到纯溶质并回收溶剂。
9.1.2 吸收过程的分类吸收过程可按多种方法分类1.按过程有无化学反应分类(1) 物理吸收~在吸收过程中,如果溶质与溶剂之间不发生明显的化学反应,可看做是气体中可溶组分单纯溶解于液相的物理过程,称为物理吸收。
用水吸收二氧化碳、用洗油吸收芳烃等过程都属于物理吸收。
(2) 化学吸收~如果溶质与溶剂发生显著的化学反应,则称为化学吸收。
用硫酸吸收氨、用碱液吸收二氧化碳等过程均为化学吸收。
2.按被吸收的组分数目分类(1) 单组分吸收~混合气体中只有一个组分进入液相,其余组分不溶解于溶剂中,称为单组分吸收。
例如合成氨原料气中含有N2、H2、CO、CO2等组分,而只有CO2一个组分在高压水中有较为明显的溶解度,这种吸收过程属于单组分吸收过程。
第九章 吸收1 焦炉煤气含粗苯330Nm g (克/标准态米3),流量h Nm 310000,经洗油吸收后降为35.1Nm g ,求粗苯的吸收率和吸收量。
设粗苯的平均分子量为100。
解:现煤气中的粗苯含量很低,可用给出的浓度代替摩尔比。
按式9-1:吸收率 95.0305.111=-=-≈BA C C ϕ吸收量 ()hr kg G A 285105.130100003=-≈注:若按摩尔比计算,则粗苯的初始组成: 摩尔浓度 A C ,b 33.010030m mol ==摩尔分率 A y ,b 5107.64.2210003.0-⨯=⎪⎭⎫⎝⎛=摩尔比 A Y ,b ()31065.71-⋅⋅⨯=-=b A bA y y同理可算出其在吸收后的组成: 摩尔分率41036.34.2210001005.1-⋅⨯=⋅=a A y 41036.3-⋅⨯=a A Y 故 9504.00496.011=-=-=⋅⋅bA a A YY ϕ可见,在本题情况下,近似解法的误差很小。
2 求温度为10℃及30℃下与总压atm 1空气接触的水中,氧的最大浓度(以3m Nl 、l mg 、摩尔分率表示)及溶解度系数(以atm m g ⋅3及Pa m kmol ⋅3表示)。
氧在空气中的体积百分率为21﹪。
解:氧在水中的最大浓度即为接触状态下的平衡浓度,可由附录一查出其亨利系数E 后,按式9-5:E P X =*算出。
氧在空气中的分压 atm p 21.021.01=⨯=氧在水中的摩尔浓度 3m kmol cx c A **=式中总浓度 35.5502.181000m kmol c =≈其质量浓度332m kg c c M C A A A A ***==再换算到mg ,需乘以310。
当以体积比32m NlO 水表示时,可按以下对气体的关系换算:Nl Nm kmol 33104.224.221⨯==现将查出及计算的结果列在下表中:计算结果亦列入表中。
3 查得30℃下2SO 溶于水的平衡数据如下:试换算成总压atm 1下的x-y 关系,并在x-y 图中作出平衡曲线。
(题解中图从略)。
解:据例9-5中已得出的算式:()6.355+=a a X 及 760P P p y == 计算至三位有效数字,可得下表:4. 25℃及atm 1下,含2CO 20﹪—空气80﹪(体积)的气体31m ,与31m 的清水在容积32m 的密闭容器中接触、传质。
问2CO 在水中的最终浓度及剩余气体的总压各为多少,设空气可视为不溶于水。
若上述过程在atm 5下进行,求其结果。
解:本题中气相体积31m V =保持不变,随着2CO 的溶解,其分压A p 下降。
查附表1,25℃下2CO 在水中的亨利系数atm E 1640=,故达平衡时: x p A 1640=* (1) *A p 与x 的另一方程可从物料衡算得出: 气相失去的2CO 量: ()()kmol p P RT V N A *-=2.01 水中得到的2CO 量: ()xkmol cx N 02.1899712=⨯= 当总压atm P 1=,由21N N =,可得()()x p A 34.552.029808206.01=-⨯* (2) 将(1)式代入(2)式: x x 135316402.0=-510682.629932.0-⨯==xatm x p A 1096.01640==*故剩余气体总压 P 余atm p P A 9096.08.0=+=*当初始总压atm P 5=,仍按上述方法计算,可得: 410341.3299352.0-⨯=⨯=x atm x p A 548.01640==*P 余atm 540.4548.058.0=+⨯=以上计算中忽略了气相中水蒸气压的变化。
5 求上题在刚开始接触时的总传质推动力,分别以分压差,液相的摩尔分率差及浓度差表示。
解:以分压差表示的总推动力为*-A A p p 。
刚开始时atm p A 2.0=,0=*A p ,故atm p p A A 2.0=-*。
以液相摩尔分率差表示时:kmol kmolA x x 41022.1016402.0-*⨯=-=- 以液相摩尔浓度差表示时:()()()3341075.61022.102.18997m kmil x x c c c A A --**⨯=⨯=-=- 当总压atm P 5=时,总推动力为上述的五倍。
6 在填料塔中用水吸收气体中所含的丙酮蒸气,操作温度20℃,压力atm 1,若已知传质系数atm s m kmol k G ⋅⋅⨯=-24105.3,s m k L 4105.1-⨯=,平衡关系服从亨利定律,亨利系数atm E 32=;求传质系数G K ,L K ,X K ,Y K 以及气相阻力在总阻力中所占的比例。
解:已知两相的传质系数G k 、L k ,可按式9-17求总传质系数G K :LG G Hk k K 111+=式中溶解度系数atm m kmol E C H ⋅===3734.1325.55 故 atm s m kmol K G ⋅⋅⨯=⨯⨯+⨯=---244410492.1105.1734.11105.311按传质系数间的换算式,可得y s m kmol P K K G Y ∆⨯==-2410492.1H K K GL =734.15.5510492.14⨯⨯===-HCK C K K G L Xx s m kmol ∆⨯=-231078.4341033.85.55105.1--⨯=⨯⨯==C k k L X气相阻力在总阻力中所占的比例为:R 气/R 总426.0844.385.2857.211=+==GGK k 或6.42﹪7 根据以下双塔吸收的四个流程图,分别作出其平衡线和操作线的示意图,并说明各适用于那些情况。
设吸收液最初不含溶质。
解:流程(Ⅰ)相当于一个气液逆流的单塔。
当所需填料甚高,单塔有困难时,用双塔(或多塔)逆流操作。
流程(Ⅱ)中每塔都送入新鲜溶剂,使全过程的推动力较流程Ⅰ为大。
适用于气体净化要求高、所需溶剂量大的情况。
流程(Ⅲ)中气体并流、液体逆流,适用于气体中溶质含量少、易吸收(通常是伴有快速反应)、要求液相浓度相对高的情况。
流程(Ⅳ)中第2塔气液并流,适用于伴有化学反应,或液量大大超过吸收所需,故推动力与并逆流关系不大的情况。
8 例9-6对每2m 塔截面共可回收多少丙酮(以h kg 计)?若将填料层高度减少31,回收量会减少多少?解:在例9-6中已求出b Y 及a Y ,丙酮回收量可按下式计算()()136001⨯⨯--=A a b b A M Y Y y G G()()hkg 7.12236005810630997.002.04=⨯⨯⨯-⨯=-当填料层高减少31,则气相总传质单元数减为()28.631139.9=-, 而吸收因数4.1=A 不变。
代入式9-56,计算新的ab y y :⎪⎭⎫ ⎝⎛=4.04.126.6㏑5.34.114.14.0=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛a a a b mx y mx y ㏑()⎥⎦⎤⎢⎣⎡+714.05.3a b y y 其中()⎥⎦⎤⎢⎣⎡+714.05.3a b y y =exp ()98.55.326.6= 则()43.18714.090.55.3=-=a b y y 00163.043.1803.0==a y 回收率()()947.00309.000163.011111=-=---=-='b ba ab a y y y y Y Y ϕ回收量()()h kg M Gy G A b 7.1183600589473.003.002.03600=⨯⨯⨯⨯=⨯⨯'='ϕ 回收量的减少为h kg G G A A 0.47.1187.122=-='-减少的相对量为033.07.1220.4==⎪⎭⎫ ⎝⎛'-AA A G G G 或3.3﹪9 若在例9-6中使出塔水的丙酮为80﹪饱和,其他数据不变,求所需的水量和填料层高度。
解:现出塔水中的丙酮的摩尔分率为01371.075.18.08.0=⎪⎭⎫ ⎝⎛==*b b b y x x而b y ,a y 等不变,由物料衡算式9-38:()()()a b b a b s Y Y y G x x L --=-1 ()4108.50986.00137.0-⨯=-s L故所需用的水量为 s m kmol L s 20423.0=以下用平均推动力法求填料高度41018.6-⨯=∆a y 与例9-6相同 ()44106010240300--⨯=⨯-=-=∆b b b mx y y()()44107.2318.660ln 1018.660--⨯=⨯-=∆my()m y y y a K G h m a b y 5.154.1225.1107.23102.630025.144=⨯=⨯⨯-⨯=∆-⨯=-- 10 在填料塔内用稀硫酸吸收空气中的氨。
因溶液中存在游离酸,故氨的平衡分压为零。
下列三种情况下的操作条件基本相同,试求所需填料高度的比例。
(1)混合气含氨1﹪,要求吸收率为90﹪; (2)混合气含氨1﹪,要求吸收率为99﹪; (3)混合气含氨5﹪,要求吸收率为99﹪; 解:因氨的平衡分压为零,故0=*y ,而有a a y y =∆,b b y y =∆,()⎪⎭⎫ ⎝⎛-=∆a b a b m y y y y y ln于是 ⎪⎪⎭⎫ ⎝⎛=∆-=a b m ab OGy y y y y N ln 又吸收率b a y y -=1ϕ,故ϕ-=11a b y y ,而有()11ln --=φOG N 现操作条件基本相同,故三种情况下的yaOG K G H =可认为相等。
于是所需填料高度之比为:h 1 : h 2 : h 3=()111ln --φ : ()121ln --φ :()131ln --φ()11.0ln -=:()101.0ln -:()101.0ln -10lg = :100lg :100lg =1:2:211 矿石培烧炉气中含52SO ﹪,余为惰性气体,经冷却后在填料塔内以水吸收2SO 的95﹪。
塔径m 8.0,操作温度K 303,总压kPa 100;入塔炉气流量h m 31000(操作状态),水量为最小值的 1.2倍。
平衡关系见习题3。
传质系数:sPa m kmol a K G 34105-⨯=,s a K L 11052-⨯=。
(1)用水量和出塔溶液浓度。
(2)填料高度。
解:塔顶、底的气液组成可如下求出:05.0=b y ,()0526.005.0105.0=-=b Y , ()31083.20526.005.01-⨯=⨯=-=b a Y Y φ()3331063.21063.211063.2---⨯=⨯+⨯=a y 0=a x由习题3算出的平衡数据可知对05.0=b y ,有0014.0=*bx ,按式9-42,知 最小液气比 2.32000147.000263.005.0min=--=--=⎪⎭⎫⎝⎛*ab a b x x y y G L 实用液气比为:7.382.1min=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛G L G L而 ()s m kmol d RT pV G 2220219.08.0785.0303314.8360010001004=⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=π (1)用水量 s m kmol L 2848.00219.07.38=⨯=或以h m 3来表示用水量:()996188.0785.036002⨯⨯='L L m 38.27= 出塔溶液中2SO 浓度为:001225.02.100147.02.1===*bb x x (2)填料高度应用例9-7所示的方法。