算法分析(2)_2016

143计算机教育Computer Education第 3 期2016 年 3 月 10 日中图分类号：G6420 引 言算法设计与分析课程是高等学校计算机科学与技术及其相关专业的核心课程，如计算机科学与技术专业、软件工程专业、信息安全专业、信息与计算科学专业、管理信息系统专业、通信工程专业等。

该课程旨在培养学生使用计算机分析问题、解决问题的能力，并掌握算法设计的基本方法。

由于算法分析与设计涉及的专业广、学生的层次多，因此，探索算法分析与设计的教学模式与方法正日益引起广大教育者的重视[1]。

当前算法设计与分析课程的教学，普遍存在以下问题：①学生缺乏学习算法的自觉性和积极性；②学生比较厌烦算法的教学内容，对课程的重视程度不够；③教学方法过于简单陈旧；④传统的教学侧重于知识的传授，对学生的学习兴趣等因素重视不够[2]。

这些问题严重影响了算法设计与分析课程教学的效果与质量。

笔者多年从事算法设计与分析课程的教学，不但在教学方法、教学手段上进行了多次有效的改革，同时特别重视第一堂课的引导教学，通过设计“百钱买百鸡问题”教学案例，充分培养学生的学习兴趣，为该课程的学习打下较好的兴趣基础。

“百钱买百鸡问题”教学案例的具体设计方法首先要求学生根据自己所学的知识完成程序设计，然后在分析时间复杂度的基础上，结合初中数学问题引导学生不断进行算法优化，最终从1 000 000次运算优化到4次运算。

在教学过程中，教师加强引导，注重交流，给合数学问题进行算法设计与分析。

学生不但理解了算法优化的重要性，而且认识到在解决问题的过程中结合数学问题进行算法设计的必要性，进一步激发了其学习兴趣，为该课程的学习打下了较好的基础。

1 百钱买百鸡问题描述“百钱买百鸡问题”记载于中国古代约5~6世纪成书的《张邱建算经》中，是原书卷下第38题，也是全书的最后一题。

该问题的描述为：今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。

凡百钱买鸡百只，问鸡翁、母、雏各几何[3]？翻译与现代汉语的意思是：公鸡每只值5文钱，母鸡每只值3文钱，而3只小鸡值1文钱。

一. 单项选择（每小题3分，总共15分）( A ) 1、在如下的有向图中，从V 1到V 4长度为3 的道路有（ A ）条。

A ． 1；B ．2；C ．3；D ．4 。

( B ) 2、假设S 、T 是两个有限集合。

那么下面正确的是：A. |S ∪T| = |S| + |T|B. |S ∪T| = |S| + |T| - |S ∩T|C. |S ×T|= |S| × |T| - |S ∩T|D. |S-T|= |S| - |T|( B )3、假定递归算法把一个规模为n 的问题分解为a 个子问题，每个子问题规模为n /b . 再假定把子问题的解组合成原来问题的解的算法处理中，需要总量为g (n )的运算数. 用f (n )表示求解规模为n 的问题所需的运算数，则得出运算数f (n )的递推关系为：A ．f (n ) = b f (n /a) + g (n )；B ．f (n ) = af (n /b ) + g (n )；C ．f (n ) = f (n /b ) +a g (n )；D ．f (n ) = ag (n /b ) + f(n )；( D ) 4、如果两个图H 与G 同构，且结点数大于1，则下面不正确的是：A ．如果H 有一个子图是非平面图，则G 是非平面图B ．如果H 是连通图，则G 没有孤立点。

C ．H 是偶图则G 也是偶图，反之也成立D ．f 是H 的结点集到G 的结点集的双射，则H 的任一结点h 的度数等于G 中结点f(h)的度数。

( D ) 5、下面说法不正确的是：A ：不同算法求出的两个不同结点的最短通路的长度是一样的。

B: 不同算法求得的两个不同结点的最短通路可能不一样。

C: 连通有权图的任两个不同结点的最短通路一定是存在的。

D ：最短通路未必就是简单路。

二. 填空（每小题3分，总共15分）1、连通无向图有欧拉开路（非回路）的充要条件是2、 83个不同的盒子中,5、三. 解答题（总共40分，每小题5分）1、一个(n,m)简单无向图是2-色图(m>0)，那么它上面的所有回路是否都是偶数长？为什么？解答：简单无向图是2-色图(m>0) 就必然是偶图。

数据结构复习要点1.选择题（12小题，24分）2.填空题（8小题，16分）3.解答题（5小题，44分）4.算法设计题（2小题，16分）第一章绪论数据结构、数据类型逻辑结构、物理结构逻辑地址、物理地址线性结构、非线性结构（树、图）算法、算法分析（时间复杂度、空间复杂度）第二章线性表线性表、线性关系（前驱、后继）顺序表（插入、删除、查找）链表（插入、删除、查找）*第三章栈和队列栈特点（先进后出）栈的基本操作（入栈、出栈、取栈顶元素）顺序栈的实现（Init/Push/Pop/GetTop）队列特点（先进先出）队列的基本操作（入列、出列）第四章串字符串、空串、空格串串的长度、串相等的条件串的基本操作（SUBSTR/INDEX/CONCA T）第五章数组和广义表二维数组存储（行优先、列优先）二维数组任意元素aij的地址计算稀疏矩阵的压缩存储（三元组、十字链表）广义表特点（层次）广义表的表头、表尾、长度、深度广义表的实现（Head/Tail）第六章树二叉树的概念（完全二叉树、满二叉树、与度为2的树的区别）二叉树的性质（5个）及应用二叉树的遍历（先序、中序、后序）及应用算法*线索二叉树（线索化）最优二叉树（Huffman）的构造及WPL计算*第七章图图（有向图、无向图、有向网、无向网）完全图（有向完全图、无向完全图）图的存储（邻接表、邻接矩阵）*图的遍历（深度、广度）*最小生成树（普里姆、克鲁斯卡尔）* 最短路径关键路径第八章查找顺序查找、折半查找二叉排序树哈希表的构造和平均查找长度的计算* 第九章排序冒泡排序*快速排序*注：有星号标记的表示有大题。

专题04 算法、推理与数学文化纵观近几年高考，算法、推理部分以数学文化为背景的问题，层出不穷，让人耳目一新。

同时它也使考生们受困于背景陌生，阅读受阻，使思路无法打开。

本专题通过对典型高考问题的剖析、数学文化的介绍、及精选模拟题的求解，让考生提升审题能力，增加对数学文化的认识，进而加深对数学文理解，发展数学核心素养。

【例1】（2016•新课标Ⅱ）中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x＝2，n＝2，依次输入的a为2，2，5，则输出的s＝（）A．7 B．12 C．17 D．34【答案】C【解析】∵输入的x＝2，n＝2，当输入的a为2时，S＝2，k＝1，不满足退出循环的条件；当再次输入的a为2时，S＝6，k＝2，不满足退出循环的条件；当输入的a为5时，S＝17，k＝3，满足退出循环的条件；故输出的S值为17，故选：C．【试题赏析】本题以秦九韶算法为文化背景，考查程序框图，当循环次数不多，或有规律可循时，可采用模拟程序法进行解答．【例2】(2015·全国卷Ⅱ) 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b分别为14,18，则输出的a＝（）A．0 B．2 C．4 D．14【答案】B【解析】(方法一)逐次运行程序，直至程序结束得出a值．输入a＝14，b＝18.第一次循环，14≠18且14<18，b＝18－14＝4；第二次循环，14≠4且14>4，a＝14－4＝10；第三次循环，10≠4且10>4，a＝10－4＝6；第四次循环，6≠4且6>4，a＝6－4＝2；第五次循环，2≠4且2<4，b＝4－2＝2；第六次循环，a＝b＝2，跳出循环，输出的a＝2，故选B.(方法二)此程序的功能是求18,14的最大公约数，因为18,14的最大公约数为2，所以输出的a＝2，选B. 【试题赏析】此题源于《九章算术·方田》，后人称之为“更相减损术”．“更相减损术”实质上是用来求两数的最大公约数，国外的欧几里得算法也可以解决这个问题．此题以“更相减损术”为载体，考查程序框图的应用，这样的设计，不仅可以让学生了解数学文化，形成理性思维，同时也能使学生感受我国古代数学的成就，增强民族自豪感.【例3】（2019课标Ⅱ文）在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．甲：我的成绩比乙高．乙：丙的成绩比我和甲的都高．丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为（）A．甲、乙、丙B．乙、甲、丙C．丙、乙、甲D．甲、丙、乙【答案】A【解析】由题意，可把三人的预测简写如下：甲：甲＞乙．乙：丙＞乙且丙＞甲．丙：丙＞乙．∵只有一个人预测正确，∴分析三人的预测，可知：乙、丙的预测不正确．如果乙预测正确，则丙预测正确，不符合题意．如果丙预测正确，假设甲、乙预测不正确，则有丙＞乙，乙＞甲，∵乙预测不正确，而丙＞乙正确，∴只有丙＞甲不正确，∴甲＞丙，这与丙＞乙，乙＞甲矛盾．不符合题意．∴只有甲预测正确，乙、丙预测不正确，甲＞乙，乙＞丙．故选：A．【试题赏析】本题以“一带一路”为文化背景，考查合情推理，因为只有一个人预测正确，所以本题关键是要找到互相关联的两个预测入手就可找出矛盾．从而得出正确结果．【例4】（2014•陕西）观察分析下表中的数据：多面体面数（F）顶点数（V）棱数（E）三棱柱 5 6 9五棱锥 6 6 10立方体 6 8 12猜想一般凸多面体中F，V，E所满足的等式是．【解析】凸多面体的面数为F、顶点数为V和棱数为E，①正方体：F＝6，V＝8，E＝12，得F+V﹣E＝8+6﹣12＝2；②三棱柱：F＝5，V＝6，E＝9，得F+V﹣E＝5+6﹣9＝2；③三棱锥：F＝4，V＝4，E＝6，得F+V﹣E＝4+4﹣6＝2．根据以上几个例子，猜想：凸多面体的面数F、顶点数V和棱数E满足如下关系：F+V﹣E＝2再通过举四棱锥、六棱柱、…等等，发现上述公式都成立．因此归纳出一般结论：F+V﹣E＝2，故答案为：F+V﹣E＝2【试题赏析】本题以欧拉公式为文化背景，考试通过观察它们的顶点数、面数和棱数，归纳出一般结论，得到欧拉公式，着重考查了归纳推理和凸多面体的性质等知识．1．《孙子算经》《孙子算经》是中国古代重要的数学著作．成书大约在四、五世纪，也就是大约一千五百年前．全书共分三卷：上卷详细地讨论了度量衡的单位和筹算的制度和方法．中卷主要是关于分数的应用题，包括面积、体积、等比数列等计算题．下卷对后世的影响最为深远，如下卷第31题即著名的“鸡兔同笼”问题，后传至日本，被改为“鹤龟算”．2．《数书九章》《数书九章》成书于1247年，是南宋数学家秦九韶唯一的数学著作，在长期艰苦的环境中写成的．全书共十八卷，分“大衍”“天时”“田域”“测望”“赋役”“钱谷”“营建”“军旅”“市物”等九类，每类九个问题，共81题．《数书九章》是一部划时代的巨著，内容丰富，精湛绝伦．秦九韶在《数书九章》中所发明的“大衍求—术”，即现代数论中一次同余式组解法，是中世纪世界数学的最高成就，比西方数学家高斯建立的同余理论早500多年，被西方称为“中国剩余定理”．此外，秦九韶还创拟了正负开方术，即任意高次方程的数值解法，也是中世纪世界数学的最高成就，秦九韶所发明的此项成果比1819年英国人霍纳的同样解法早500多年．1. (2019洛阳模拟) 秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例．若输入n，x的值分别为4,3，则输出v的值为（）A．20 B．61 C．183 D．548【答案】C【解析】由程序框图知，初始值：n＝4，x＝3，v＝1，i＝3，第一次循环：v＝6，i＝2；第二次循环：v＝20，i＝1；第三次循环：v＝61，i＝0；第四次循环：v＝183，i＝1.结束循环，输出当前v的值183.2.(2019青岛联考)如图所示的程序框图的算法数学思想源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图(图中“m MOD n”表示m除以n的余数)，若输入的m，n分别为495,135，则输出的m＝（）A．0 B．5 C．45 D．90【答案】C【解析】该程序框图是求495与135的最大公约数，由495＝135×3＋90,135＝90×1＋45,90＝45×2，所以495与135的最大公约数是45，所以输出的结果是45.3．（2019四川模拟）我国古代数学名著《孙子算经》有鸡兔同笼问题，根据问题的条件绘制如图的程序框图，则输出的x，y分别是（）A．12，23 B．23，12 C．13，22 D．22，13【答案】B【解析】由程序框图，得：x＝1，y＝34，S＝138；x＝3，y＝32，S＝134；x＝5，y＝30，S＝130；x＝7，y＝28，S＝126；……，x＝23，y＝12，S＝94．输出x＝23，y＝12．故选：B．4.（2019黄石二模）公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π.他从圆内接正六边形算起，令边数一倍一倍地增加，逐个算出正六边形，正十二边形，正二十四边形，……的面积，这些数值逐步地逼近圆的面积，刘徽一直计算到正3072边形，得到了圆周率π的近似值3.1416.刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的，用有限来逼近无限．这种思想极其重要，对后世产生了巨大影响．如图是利用刘徽的“割圆术”思想设计的一个程序框图．若运行该程序(参考数据：3≈1.732，sin 15°≈0.2588，sin 7.5°≈0.1305)，则输出的n 的值为（ ）A ．48B ．36C ．30D ．24【答案】D【解析】输入n 的值为6；第一次循环，S ＝3sin 60°＝332<3.10，n ＝12； 第二次循环，S ＝6sin 30°＝3<3.10，n ＝24；第三次循环，S ＝12sin 15°≈3.1056>3.10，退出循环，则输出的n 的值为24.5．（2019汉中联考）1927年德国汉堡大学的学生考拉兹提出一个猜想：对于任意一个正整数，如果它是奇数，对它乘3加1，如果它是偶数，对它除以2，这样循环，最终结果都能得到1.有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步，将开辟全新的领域”.如图是根据考拉兹猜想设计的一个程序框图，则输出i 的值为（ ）A ．8B ．7C ．6D ．5【答案】A【解析】3a =，1a =不满足，a 是奇数满足，10a =，2i =，10a =，1a =不满足，a 是奇数不满足，5a =，3i =，5a =，1a =不满足，a 是奇数满足，16a =，4i =，16a =，1a =不满足，a 是奇数不满足，8a =，5i =，8a =，1a =不满足，a 是奇数不满足，4a =，6i =，4a =，1a =不满足，a . 是奇数不满足，2a =，7i =，2a =，1a =不满足，a 是奇数不满足，1a =，8i =，1a =，1a =满足，输出8i =，故选A ．6. (2019深圳模拟)中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而等长．意思是现有松树高5尺，竹子高2尺，松树每天长自己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一样高？如图是源于其思路的一个程序框图，若输入的x ＝5，y ＝2，输出的n 为4，则程序框图中判断框中应填入( )A ．y ≤x?B ．x ≤y?C ．y <x?D ．x ＝y?【答案】B【解析】根据程序框图，输入x ＝5，y ＝2，n ＝1.第一次循环，x ＝5＋52＝152，y ＝4，此时y <x ；第二次循环，n ＝2，x ＝152＋154＝454，y ＝8，此时y <x ； 第三次循环，n ＝3，x ＝454＋458＝1358，y ＝16，此时y <x ；第四次循环，n ＝4，x ＝1358＋13516＝40516，y ＝32，此时y ≥x ，输出n 的值4.由此可知，应填的条件是x ≤y ？.7. (2019包头模拟)我国古代的劳动人民曾创造了灿烂的中华文化，戍边的官兵通过在烽火台上举火向国内报告，烽火台上点火表示数字1，不点火表示数字0.这蕴含了进位制的思想．如图所示的程序框图的算法思路就源于我国古代戍边官兵的“烽火传信”．执行该程序框图，若输入a＝110011，k＝2，n＝6，则输出b的值为（）A．19 B．31 C．51 D．63【答案】C【解析】(方法一)输入a＝110011，k＝2，n＝6，输入b＝0，i＝1.第一次循环，输入t＝1，b＝0＋1×20＝1，i＝2,2>6不成立；第二次循环，输入t＝1，b＝1＋1×21＝3，i＝3,3>6不成立；第三次循环，输入t＝0，b＝3＋0×22＝3，i＝4,4>6不成立；第四次循环，输入t＝0，b＝3＋0×23＝3，i＝5,5>6不成立；第五次循环，输入t＝1，b＝3＋1×24＝19，i＝6,6>6不成立；第六次循环，输入t＝1，b＝19＋1×25＝51，i＝7,7>6成立，退出循环，输出b的值为51.(方法二)将二进制数化为十进制数，a＝110011(2)＝1×25＋1×24＋0×23＋0×22＋1×21＋1×20＝51.故b的值为51.8．（2019长沙模拟）如图，一块黄铜板上插着三根宝石针，在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片：每次只能移动一片金片；每次移动的金片必须套在某根针上；大片不能叠在小片上面.设移完片金片总共需要的次数为，可推得.求移动次数的程序框图模型如图所示，则输出的结果是（）A．1022 B．1023 C．1024 D．1025【答案】B【解析】记个金属片从号针移动到号针最少需要次；则据算法思想有：；第一次循环，；第二次循环，；第三次循环，，…，第九次循环，，输出，故选B.9．（2019•九江三模）2018年9月24日，阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想，这一事件引起了数学界的震动，在1859年，德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题，也就是著名的黎曼猜想．在此之前，著名数学家欧拉也曾研究过这个问题，并得到小于数字x的素数个数大约可以表示为n（x）的结论（素数即质数，lge≈0.43429）．根据欧拉得出的结论，如下流程图中若输入n的值为100，则输出k的值应属于区间（）A．（15，20] B．（20，25] C．（25，30] D．（30，35]【答案】B【解析】该流程图是统计100以内素数的个数，由题可知小于数字x的素数个数大约可以表示为n（x）≈；则100以内的素数个数为：n（100）≈＝＝＝50lge≈22．故选：B．10．（2019银川二模）原始社会时期，人们通过在绳子上打结来计算数量，即“结绳计数”，当时有位父亲，为了准确记录孩子的成长天数，在粗细不同的绳子上打结，由细到粗，满七进一，那么孩子已经出生多少天？（）A．1 326 B．510 C．429 D．336【答案】B【解析】由题意满七进一，可得该图示为七进制数，化为十进制数为1×73＋3×72＋2×7＋6＝510. 11．（2019•天河区校级三模）将杨辉三角中的奇数换成1，偶数换成0，得到如右图所示的0﹣1三角数表．从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第2n﹣1行；则第61行中1的个数是（）A．31 B．32 C．33 D．34【答案】B【解析】由已知图中的数据第1行 1 1第2行 1 0 1第3行 1 1 1 1第4行 1 0 0 0 1第5行 1 1 0 0 1 1…∵全行都为1的是第2n﹣1行；∵n＝6时，26﹣1＝63，故第63行共有64个1，逆推知第62行共有32个1，第61行共有32个1．故y＝32，故选：B．12．（2019•成都模拟）“幻方’’最早记载于我国公元前500年的春秋时期《大戴礼》中．“n阶幻方（n≥3，n∈N*）”是由前，n2个正整数组成的﹣个n阶方阵，其各行各列及两条对角线所含的n个数之和（简称幻和）相等，例如“3阶幻方”的幻和为15（如表所示）．则“5阶幻方”的幻和为（）8 1 63 5 74 9 2A．75 B．65 C．55 D．45【答案】B【解析】由1，2，3，4…24，25的和为＝325，又由“n阶幻方（n≥3，n∈N*）”的定义可得：“5阶幻方”的幻和为＝65，故选：B．13．（2019•龙泉驿区模拟）如图所示，正方形上连接着等腰直角三角形，等腰直角三角形腰上再连接正方形，…，如此继续下去得到一个树形图形，称为“勾股树”．若某勾股树含有255个正方形，且其最大的正方形的边长为，则其最小正方形的边长为（）A．B．C．D．【答案】A【解析】由题意，正方形的边长构成以为首项，以为公比的等比数列，现已知共得到255个正方形，则有1+2+…+2n﹣1＝255，∴n＝8，∴最小正方形的边长为×（）7＝．故选：A．14．（2019•拉萨三模）英国统计学家E．H．辛普森1951年提出了著名的辛普森悖论，下面这个案例可以让我们感受到这个悖论．有甲乙两名法官，他们都在民事庭和行政庭主持审理案件，他们审理的部分案件被提出上诉．记录这些被上述案件的终审结果如表所示（单位：件）：记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为x1，x2和x，记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为y1，y2和y，则下面说法正确的是（）A．x1＜y1，x2＜y2，x＞y B．x1＜y1，x2＜y2，x＜yC．x1 ＞y1，x2 ＞y2，x＞y D．x1 ＞y1，x2＞y2，x＜y【答案】D【解析】由图表可知：x1＝＝0，90625，y1＝＝0，9，即x1＞y1，x2＝≈0.85，y2＝＝0.8，即x2＞y2，x＝＝0.86，y＝＝0.88，即x＜y，即x1＞y1，x2＞y2，x＜y，故选：D．15．（2019株洲二模）高铁是一种快捷的交通工具，为我们的出行提供了极大的方便。

计算机教学论文：聚焦计算思维的算法分析与设计课程教学改革0 引言算法是计算机科学中最具方法论性质的核心概念，被誉为计算机学科的灵魂。

图灵奖获得者Niklaus Wirth提出：算法+数据结构=程序，强调了算法在计算机领域的重要性。

在现实生活中，算法、算据和算力组成了人工智能技术的三要素；算法的新颖性和性能决定了学术论文在高水平期刊或会议上发表的可能性；算法能力测试是研究生复试和求职面试等场合常见的环节。

因此，学习并掌握好算法相关知识，对一名本科生的综合能力培养和职业发展来说非常重要。

国内外各大高校计算机专业在培养方案中，普遍开设了算法分析与设计（以下简称算法）课程，该课程以高级程序设计和数据结构为先导课程，又为人工智能等专业课程提供算法支撑，是培养方案的重要枢纽之一。

算法课程既包含抽象的理论，又强调算法的实践，对学生的逻辑思维和计算建模等能力有较高的要求，因此有必要聚焦计算思维，开展面向能力提升的课程教学改革。

1 课程教学和改革现状1.1 共性问题目前，采取小班化策略开展算法课程教学已比较普遍；多数高校选用MIT经典书籍《Introduction to Algorithms》作为教材；依托在线平台开展编程训练取得了良好的教学效果。

但在教学过程中，还存在一些共性问题。

（1）学生在理论学习时普遍存在畏难心理。

算法要求学生不仅掌握算法的实施，更强调对算法原理的理解；一些关键的算法要进行证明，如主方法、最优前缀码等，这需要大量的理论知识，涉及不少数学符号，学生容易感到枯燥和抽象，降低了学习兴趣。

（2）学生难以灵活运用算法解决实际问题。

学生往往能够较好地掌握教材中的经典问题和相应的算法，并完成课后习题和部分在线训练题，但遇到复杂的现实问题或工程问题时，要么没有思路，要么依赖直觉，无法准确构建输入输出间的解析关系。

（3）学生的基础水平和学习需求差异明显。

修读课程的学生水平参差不齐，学习动力和学习方法也各不相同，因此处在两极的学生的学习需求通常难以得到精细满足；另外，创新实验活动和程序设计竞赛吸引了部分学有余力的学生，但课程教学和第二课堂缺乏深度结合。

无线传感器网络中的能耗优化算法分析引言无线传感器网络是一种由成千上万个分布在特定区域内的无线传感器节点组成的网络，这些节点可以自组织地协同工作，实现数据的采集、处理和传输。

然而，无线传感器网络中的节点能源有限，因此如何优化能耗是该领域的重要研究方向之一。

本文将对无线传感器网络中的能耗优化算法进行分析和讨论。

一、能耗分析在无线传感器网络中，节点的能耗主要来自于通信、计算和感知三个方面。

通信能耗是指节点之间进行通信所消耗的能量，包括传输能耗和接收能耗。

计算能耗是指节点进行数据处理和算法运算所消耗的能量。

感知能耗是指节点进行环境感知和数据采集所消耗的能量。

因此，能耗优化的关键是减少通信能耗、计算能耗和感知能耗三个方面的消耗。

二、能耗优化算法（一）路由优化算法路由优化算法是通过合理地选择和部署传感器节点之间的通信路径，来减少通信能耗。

其中，LEACH（Low-Energy Adaptive Clustering Hierarchy）是一种常用的路由协议，通过动态地将节点划分为簇，每个簇有一个簇首节点负责聚集和传输数据，从而减少了通信能耗。

（二）任务调度算法任务调度算法是通过合理地分配节点的计算任务，来减少计算能耗。

其中，多处理器任务调度算法可以将计算任务分配到多个节点上并行执行，从而减少计算时间和能耗。

此外，还可以通过对任务进行优先级排序，合理安排任务执行的顺序，进一步降低计算能耗。

（三）能量平衡算法能量平衡算法是通过动态地调整节点之间的能量消耗，来平衡网络中各个节点的能量消耗，从而延长网络的生命周期。

其中，一种常用的方法是通过控制节点的传输功率来均衡能量消耗，即使网络中各个节点的能量消耗趋于平衡。

（四）移动节点优化算法移动节点优化算法是通过调整节点的位置，来优化能耗。

例如，可以通过移动节点的位置，使得节点之间的通信距离减小，从而减少通信能耗。

此外，还可以通过调整节点在网络中的密度分布，来平衡能量消耗。

node2vec算法原理
node2vec算法是一种用于学习节点嵌入的方法，它可以在图形数据中捕获节点之间的复杂关系。

该算法由斯坦福大学的Aditya Grover和Jure Leskovec于2016年提出。

node2vec算法的原理可以从以下几个方面来解释：
1. 随机游走（Random Walks），node2vec算法首先通过随机游走来模拟节点之间的邻近关系。

随机游走是指从图中的某个节点出发，按照一定的策略选择下一个访问的节点，不断重复这个过程直到达到预设的步数。

这样可以得到一系列节点序列，反映了节点之间的邻近关系。

2. 节点嵌入（Node Embedding），在得到随机游走的节点序列后，node2vec算法通过将这些序列映射到低维向量空间中，从而得到每个节点的嵌入表示。

这个嵌入表示可以捕获节点之间的结构关系，使得在低维空间中相似的节点在向量空间中距离较近。

3. 两种随机游走策略，node2vec算法引入了两种不同的随机游走策略，分别是广度优先搜索（BFS）和深度优先搜索（DFS）。

这两种策略可以在节点之间进行局部性和全局性的探索，从而更好
地捕捉节点之间的结构信息。

4. 通过优化算法学习节点嵌入，最后，node2vec算法使用优化算法（如随机梯度下降）来学习节点嵌入，使得节点在嵌入空间中的相对位置能够最好地反映它们在原始图中的结构关系。

总的来说，node2vec算法通过随机游走和节点嵌入相结合的方式，能够在学习图中节点嵌入时充分考虑节点之间的邻近关系和结构信息，从而得到更加准确和全面的节点表示。

这使得node2vec算法在网络分析、社交网络挖掘、推荐系统等领域具有广泛的应用前景。

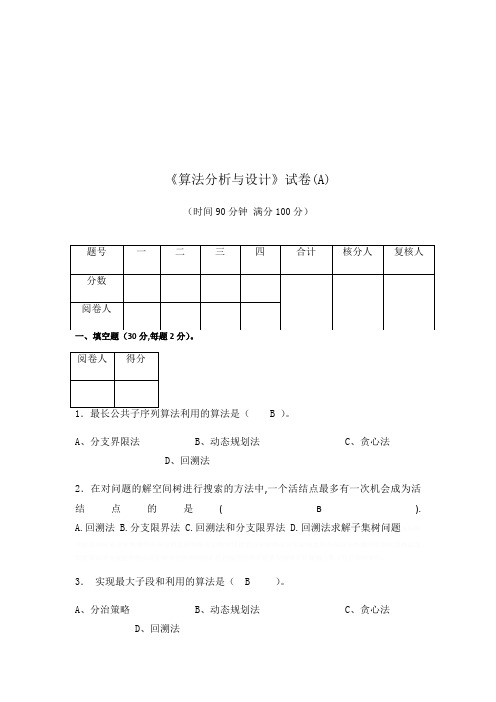
《算法分析与设计》试卷(A)（时间90分钟满分100分）B ）。

A、分支界限法B、动态规划法C、贪心法D、回溯法2．在对问题的解空间树进行搜索的方法中,一个活结点最多有一次机会成为活结点的是( B ).A.回溯法B.分支限界法C.回溯法和分支限界法D.回溯法求解子集树问题3．实现最大子段和利用的算法是（ B ）。

A、分治策略B、动态规划法C、贪心法D、回溯法4．.广度优先是（ A ）的一搜索方式。

A、分支界限法B、动态规划法C、贪心法D、回溯法5．衡量一个算法好坏的标准是（ C ）。

A 运行速度快B 占用空间少C 时间复杂度低D 代码短6．Strassen矩阵乘法是利用（ A）实现的算法。

A、分治策略B、动态规划法C、贪心法D、回溯法7. 使用分治法求解不需要满足的条件是（ A ）。

A 子问题必须是一样的B 子问题不能够重复C 子问题的解可以合并D 原问题和子问题使用相同的方法解8．用动态规划算法解决最大字段和问题，其时间复杂性为( B ).A.lognB.nC.n2D.nlogn9.解决活动安排问题，最好用（ B ）算法A.分治B.贪心C.动态规划D.穷举10.下面哪种函数是回溯法中为避免无效搜索采取的策略（ B ）A．递归函数 B.剪枝函数C。

随机数函数 D.搜索函数11. 从活结点表中选择下一个扩展结点的不同方式将导致不同的分支限界法,以下除( C )之外都是最常见的方式.A.队列式分支限界法B.优先队列式分支限界法C.栈式分支限界法D.FIFO分支限界法12. .回溯算法和分支限界法的问题的解空间树不会是( D ).A.有序树B.子集树C.排列树D.无序树13.优先队列式分支限界法选取扩展结点的原则是（ C ）。

A、先进先出B、后进先出C、结点的优先级D、随机14．下面是贪心算法的基本要素的是（ C ）。

A、重叠子问题B、构造最优解C、贪心选择性质D、定义最优解15．回溯法在解空间树T上的搜索方式是( A ).A.深度优先B.广度优先C.最小耗费优先D.活结点优先二、填空题（20分,每空1分）。

多尺度Retinex算法的分析与改进李涛【摘要】传统Retinex算法中,从图像中完全去除亮度分量而使用反射分量来增强效果.通常图像光照变化并非平缓,使得结果图像视觉效果缺乏协调.对此提出一种改进的Retinex算法,通过再处理亮度分量,得到平缓的亮度图像并补偿到反射分量从而改善增强效果,使用均值模版代替高斯模版以减少计算的时间,同时利用拉普拉斯算子加入图像边缘细节特征.实验通过处理低对比度、低亮度的X光射线将改进的Retinex方法与其他各种增强算法进行对比.对实验结果的定性和定量分析表明了该改进算法的有效性.【期刊名称】《微型机与应用》【年(卷),期】2016(035)004【总页数】4页(P40-43)【关键词】多尺度Retinex;均值模版;平滑光照;拉普拉斯算子【作者】李涛【作者单位】四川大学计算机学院,四川成都610065【正文语种】中文【中图分类】TP391图像增强是图像分析、图像分割等其他图像处理的预处理，其目标是满足人眼的需要有选择性地强调或者抑制图像中的某些信息[1]。

目前，有许多的增强方法经常出现在各个应用中，例如伽马校正、直方图均衡化和小波变换等[2]，对图像增强的发展起到了一定的引导作用，但各自表现出明显的不足。

1977年，LAND E H根据人类视觉中对光照和色彩感知提出了Retinex模型[3]。

Retinex理论就是去除图像中亮度信息而保留反射信息来恢复物体的原始信息，从而达到增强效果。

然而，当图像中光照分布不均匀或者光照不是平缓变化时，仅仅通过滤波器得到的反射分量不能完全满足要求。

针对Retinex算法存在的一些不足，通过对亮度分量进行滤波处理以补偿增强后的图像；算法过程中存在大量的卷积操作，大大降低了算法运算效率，根据大尺度高斯模版的均值特性，使用均值模版代替高斯模版对图像进行滤波操作；最后通过拉普拉斯算子增加图像的细节信息。

根据Retinex理论将图像视为物体亮度分量L(x,y)和反射分量R(x,y)，则真实图像函数I(x,y)表达式为：I(x,y)=R(x,y)*L(x,y)LAND E H在此基础上扩展提出中心/环绕Retinex算法[4](即局部Retinex)，JOBSON D J[5]等人在中心/环绕Retinex的基础上，提出了单尺度的Retinex算法，该算法的数学公式为：R(x,y)=logI(x,y)-log[I(x,y)*F(x,y)]其中，R(x,y)表示输出的图像；*为卷积运算；F(x,y)表示中心/环绕函数，一般采用高斯函数，可以达到很好的增强效果。

2016年攻读硕士学位研究生入学考试试题考试科目:计算机科学专业基础综合科目代码:874＃适用专业:计算机科学与技术.计算机应用技术.计算机技术.软件工程（试题共9页）（答案必须写在答题纸上，写在试题上不给分）数据结构与算法分析（共65分）一.单项选择题（每小题2分，共18小题，共36分）1.程序段for(i=n-1;>=1;--i)for(j=i;j<i;++j)if(A[j])ali与al+1对换;其中n为正整数，则最后一行的语句最多执行（）次。

A.O(n)B.O(n2)C.O(n3)D.O(nlogn)2.将两个有N个元素的有序表归并成一个有序表，其最少比较次数为（）。

A.NB.2NC.N-1D.2N-23.下列编码中属前缀编码的是（）A.｛1，01，000，001｝B.｛0，1，00，11C.｛0，10，110，11｝D.｛1，01，011，010｝4.在具有n个结点的有序单链表中插入一个新结点并使链表仍然有序的时间复杂度是（）A.O(1)BO(n) C.O(nlogn) D.O(n2)5.若用一个不带头结点的循环单链表表示队列，则最好用（）标识链队。

A.首结点指针B尾结点指针C.首结点和尾结点两个指针D任何结点指针6.一个10阶对称矩阵A[1...10,1...10]采用压缩存储方式，将其下三角和主对角部分按行优先存储到一维数组B[1...m]中，则A[5][8]元素在B中的位置k是（）。

A.32B.37C.45D.607.下列排序算法中元素的移动次数和关键字的初始排列次序无关的是（）A.直接插入排序B.起泡排序C.快速排序D.基数排序8.采用邻接矩阵表示一个具有n个顶点m条边的无向图，该矩阵的大小是（）。

A.2n*2mB.m*mC.n*mD.n*n9.设某哈夫曼树中有199个结点，则该哈夫曼树中有（）个叶子结点。

A.99B.100C.101D.10210.以下关于广度优先遍历算法的叙述中正确的是A.广度优先历算法不适合有向图。

10进制转4进制算法一、引言在计算机科学中，进制转换是一项重要的基础知识。

我们常用的十进制是一种常见的进制，而四进制则是一种较为特殊的进制。

本文将介绍如何将十进制数转换为四进制数的算法。

二、十进制转四进制算法1. 确定输入和输出我们需要一个十进制数作为输入，并将其转换为一个四进制数作为输出。

2. 确定算法步骤十进制转四进制的算法步骤如下：(1) 将输入的十进制数除以四，并记录商和余数。

(2) 将商作为新的十进制数，重复步骤(1)直到商为0为止。

(3) 将记录的余数按照从最后一次除法开始的顺序排列，即为输出的四进制数。

3. 算法演示我们以一个具体的例子来演示十进制转四进制的算法：假设输入的十进制数为37。

(1) 37除以4得到商9余1。

(2) 9除以4得到商2余1。

(3) 2除以4得到商0余2。

根据步骤(3)的顺序，得到的余数为211，即为输出的四进制数。

4. 算法实现下面是一个使用Python语言实现的十进制转四进制的算法示例代码：```pythondef decimal_to_quaternary(decimal):quaternary = ''while decimal > 0:quaternary = str(decimal % 4) + quaternarydecimal = decimal // 4return quaternary# 测试算法decimal_number = 37quaternary_number = decimal_to_quaternary(decimal_number) print(quaternary_number)```5. 算法分析对于给定的十进制数，我们通过除法运算和取余数的操作，将其转换为四进制数。

算法的时间复杂度是O(logn)，其中n是输入的十进制数。

三、总结本文介绍了将十进制数转换为四进制数的算法。

通过对输入的十进制数进行除法运算和取余数的操作，可以得到对应的四进制数。