全等三角形的判定(ASA)

全等三角形的判定ASA在初中数学的几何世界里，全等三角形是一个非常重要的概念。

而全等三角形的判定方法有多种，其中“ASA”（角边角）就是一种常用且重要的判定方法。

首先，咱们来理解一下什么是“ASA”。

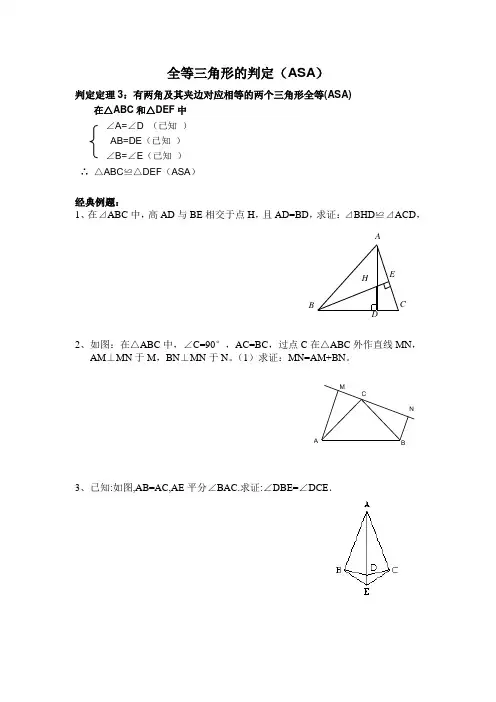
“角边角”说的就是如果两个三角形的两个角及其夹边分别相等，那么这两个三角形就是全等的。

比如说，有三角形 ABC 和三角形 DEF。

如果角 A 等于角 D，角 B等于角 E，而且 AB 这条边和 DE 这条边相等，那么就能够得出三角形ABC 全等于三角形 DEF。

那为什么“ASA”能判定两个三角形全等呢？咱们来仔细想想。

如果两个角相等，那第三个角是不是肯定也相等？因为三角形的内角和是固定的 180 度嘛。

所以两个角相等了，第三个角也就跟着相等了。

再加上夹边相等，那这两个三角形的形状和大小就完全确定了。

就好像咱们用模具做东西，角度和边都确定了，做出来的东西肯定是一模一样的。

咱们通过具体的例子来感受一下“ASA”的魅力。

假设在三角形 ABC 中，角 A 是 60 度，角 B 是 40 度，AB 边的长度是 5 厘米。

然后有另一个三角形 DEF，角 D 是 60 度，角 E 是 40 度，DE 边也是 5 厘米。

那咱们就可以很确定地说，三角形 ABC 全等于三角形 DEF。

在实际做题的时候，怎么运用“ASA”来证明两个三角形全等呢？这就需要我们仔细观察题目中给出的条件。

比如说，题目可能会告诉我们两个三角形中的一组对应角相等，然后再告诉我们这两个角之间的夹边相等。

这时候，我们就要敏锐地意识到，可以用“ASA”来证明全等。

又或者，题目中可能会通过一些角度的计算，让我们得出两个角相等，然后再给出夹边相等的条件。

咱们再来说说“ASA”和其他全等三角形判定方法的关系。

“ASA”和“AAS”（角角边）有时候容易让人混淆。

但其实“AAS”可以通过三角形内角和定理转化为“ASA”。

而“SSS”（边边边）则是通过三条边的相等来判定全等，和“ASA”的角度和边的结合方式有所不同。

12.2 全等三角形判定二（ASA ，AAS ）全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA”）.注意：如图，如果∠A ＝∠'A ，AB ＝''A B ，∠B ＝∠'B ，则△ABC ≌△'''A B C .题型1：用ASA 判定三角形全等1.已知：如图，E ，F 在AC 上，AD ∥CB 且AD ＝CB ，∠D＝∠B．求证：AE ＝CF ．【答案与解析】证明：∵AD ∥CB∴∠A ＝∠C在△ADF 与△CBE 中A C AD CBD B Ð=Ðìï=íïÐ=Ðî∴△ADF ≌△CBE （ASA ）∴AF ＝CE ，AF ＋EF ＝CE ＋EF故得：AE ＝CF【总结】利用全等三角形证明线段(角)相等的一般方法和步骤如下：(1)找到以待证角(线段)为内角(边)的【变式1-1】如图，已知AB=AC，∠B=∠C，求证：△ABE≌△ACD．【答案】证明：在△ABE和△ACD中，∵∠A=∠AAB=AC∠B=∠C，∴△ABE≌△ACD（ASA）．【解析】【分析】利用ASA证明△ABE和△ACD全等即可．【变式1-2】如图，AB=AE，∠1=∠2，∠B=∠AED．求证：△ABC≌△AED．【答案】证明：∵∠1=∠2，∴∠1+∠EAC=∠2+∠EAC,∴∠BAC=∠EAD,在△ABC与△AED中，∠BAC=∠EADAB=AE∠B=∠AED∴△ABC≌△AED(ASA)【解析】【分析】由∠1=∠2，证明∠BAC=∠EAD,再结合：AB=AE，∠B=∠AED，利用角边角公理可得结论．全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）题型2：用AAS 判定三角形全等2.已知：如图，AB ⊥AE ，AD ⊥AC ，∠E ＝∠B ，DE ＝CB ．求证：AD ＝AC ．【思路点拨】要证AC ＝AD ，就是证含有这两个线段的三角形△BAC ≌△EAD.【答案与解析】证明：∵AB ⊥AE ，AD ⊥AC ，∴∠CAD ＝∠BAE ＝90°∴∠CAD ＋∠DAB ＝∠BAE ＋∠DAB ，即∠BAC ＝∠EAD在△BAC 和△EAD 中BAC EAD B ECB=DE Ð=ÐìïÐ=Ðíïî∴△BAC ≌△EAD （AAS ）∴AC ＝AD【总结】我们要善于把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．【变式2-1】如图，在△ABC 和△CDE 中，点B 、D 、C 在同一直线上，已知∠ACB=∠E ，AC=CE ，AB ∥DE ，求证：△ABC ≌△CDE ．【答案】证明：∵AB ∥DE ，∴∠B =∠EDC ，在△ABC 和△CDE 中，∠B =∠EDC ∠ACB =∠E AC =CE，∴△ABC≌△CDE (AAS )．【解析】【分析】利用“AAS”证明△ABC≌△CDE 即可。

全等三角形的判定ASA在初中数学的几何世界里，全等三角形是一个非常重要的概念。

而判定两个三角形全等的方法有很多，其中之一便是“ASA”，也就是“角边角”。

今天，咱们就来好好聊聊这个全等三角形的判定方法 ASA。

首先，咱们得弄清楚啥是“角边角”。

简单来说，就是如果两个三角形的两个角及其夹边分别相等，那么这两个三角形就是全等的。

为了更好地理解 ASA 这个判定方法，咱们来看几个具体的例子。

比如说，有两个三角形，一个三角形的两个角分别是 30 度和 60 度，它们的夹边是5 厘米；另一个三角形也有两个角分别是30 度和60 度，并且这两个角的夹边同样是 5 厘米。

那么根据 ASA 判定方法，这两个三角形就是全等的。

那为啥 ASA 能判定两个三角形全等呢？这就得从三角形的稳定性说起啦。

当三角形的两个角和它们的夹边确定下来后，这个三角形的形状和大小就被唯一确定了。

因为三角形的内角和是 180 度，已知两个角，就能求出第三个角的度数。

而夹边的长度也确定了，所以这个三角形就被完全确定下来了，不会再有其他的变化。

接下来咱们说说怎么用 ASA 来证明两个三角形全等。

比如说，有题目给出了两个三角形，告诉咱们其中一个三角形的∠A ＝ 30 度，∠B ＝ 50 度，AB 边的长度是 8 厘米；另一个三角形中，∠D ＝ 30 度，∠E ＝ 50 度，DE 边的长度也是 8 厘米。

那咱们就可以这样来证明：因为在三角形 ABC 中，∠A ＝ 30 度，∠B ＝ 50 度，所以根据三角形内角和为 180 度，可以算出∠C ＝ 100 度。

在三角形 DEF 中，∠D ＝ 30 度，∠E ＝ 50 度，所以∠F ＝ 100 度。

又因为∠A ＝∠D ＝ 30 度，∠B ＝∠E ＝ 50 度，AB ＝ DE ＝ 8厘米，所以根据“角边角”（ASA）判定方法，三角形 ABC 全等于三角形 DEF。

再举个例子，假如有一个三角形 ABC，∠A ＝ 45 度，∠B ＝ 90 度，AB 边的长度是 6 厘米。